浙教版数学八年级上册 3.2不等式的基本性质课件(共17张PPT)
文档属性
| 名称 | 浙教版数学八年级上册 3.2不等式的基本性质课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 658.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-08 14:20:58 | ||
图片预览






文档简介
(共17张PPT)
第3章 一元一次不等式
3.2 不等式的基本性质
学习目标
1.理解不等式的三个基本性质,并能与等式的基本性质区分.
2.会用不等式的基本性质进行简单的不等式变形.
复习回顾
文字语言 符号语言
性质1
性质2
问题:等式有哪些性质?分别用文字语言和符号语言表示.
等式两边加(或减)同一个数(或式子),所得结果仍是等式
等式两边都乘以(或都除以)同一个数(除数不能为0),所得结果仍是等式
如果a=b,
那么a±c=b±c
情境引入
对于左图中的问题,你认为ac是大于bc,还是小于bc?
用几个具体的例子试试看.
猜测:ac<bc.
举例:a=4,b=2,c=-3,则ac=-12,bc=-6,那么ac<bc;
a=8,b=1,c=-5,则ac=-40,bc=-5,那么ac<bc.
…
合作探究
(1)已知a<b和b<c,在数轴上表示如图所示:
a
b
c
由数轴上a和c的位置关系,你能得出什么结论?
你能举几个具体的例子说明吗?
根据a和c的位置关系,可得出a<c.
小组合作,举出几个具体例子对此结论进行说明.
不等式的基本性质1
一
不等式的基本性质 1
a<b,b<c
这个性质也叫做不等式的传递性.
a<c.
b
a
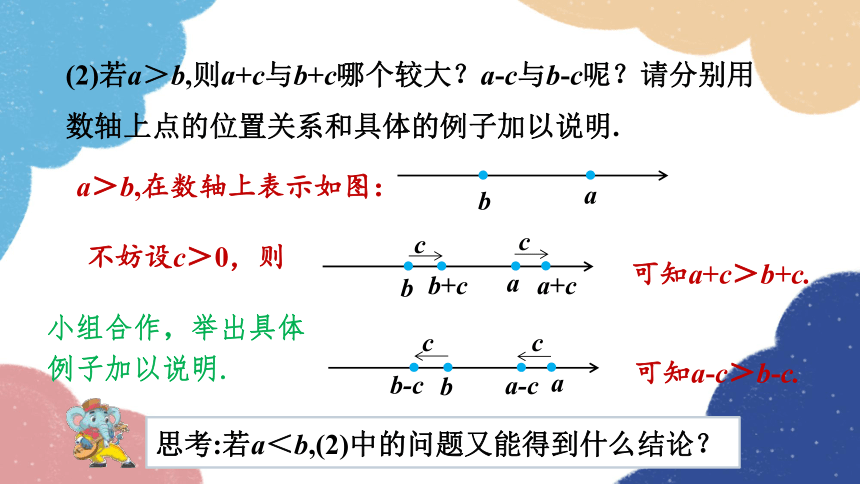
(2)若a>b,则a+c与b+c哪个较大?a-c与b-c呢?请分别用
数轴上点的位置关系和具体的例子加以说明.
a>b,在数轴上表示如图:
b
a
不妨设c>0,则
b
a
c
c
b+c
a+c
可知a+c>b+c.
c
c
b-c
a-c
可知a-c>b-c.
小组合作,举出具体例子加以说明.
思考:若a<b,(2)中的问题又能得到什么结论?
不等式的两边都加上(或减去)同一个数,
所得到的不等式仍成立.
a>b
a<b
不等式的基本性质2
二
不等式的基本性质 2
a+c>b+c,a-c>b-c;
a+c<b+c,a-c<b-c.
现在我们来考虑不等式的两边都乘(或都除以)同一个不为零的数的情况.
成立
若两边都乘-5(或除以-5)呢?
>
>
小组合作,再举几个例子试一试,能得出什么结论?
不等式的两边都乘(或都除以)同一个正数,所得的不等式仍成立;不等式的两边都乘(或都除以)同一个负数,必须改变不等号的方向,所得的不等式成立.
a>b,且c>0
a>b,且c<0
不等式的基本性质3
三
不等式的基本性质 3
例题讲解
例 已知a<0,试比较2a与a的大小.
分析:比较2a与a的大小,可以利用不等式的基本性质,也可以利用数轴,直接得出2a与a的大小.
解法一:∵2>1,a<0,(已知),
∴2a<a(不等式的基本性质3).
例题讲解
例 已知a<0,试比较2a与a的大小.
解法二:在数轴上分别标出表示2a和a的点(a<0),如图所示:
0
a
2a
2a位于a的左边,∴2a<a.
还有其他比较2a与a的大小的方法吗?
想一想
解法三:∵2a-a=a,又∵a<0,
∴2a-a<0,
∴2a<a(不等式的基本性质2).
随堂练习
1. (1)如果x<0.3,而0.3<1,那么x____1;
(2)如果a<3,而b>3,那么a_____b.
解析:(1)根据不等式的传递性可知,x<1.
(2)根据不等式的传递性可知,a<b.
<
<
2.下列说法正确的是( )
A.∵a<b,∴a+2<b+1 B.∵a<b,∴a-1<b-2
C.∵a>b,∴a+c>b+c D.∵a>b,∴a+c>b-d
C
3.由a-3<b+1,可得到结论( )
A.a<b B.a+3<b-1
C.a-1<b+3 D.a+1<b-3
C
4.若x>y,比较2-3x与2-3y的大小,并说明理由.
解:
∵x>y(已知),
∴-3x<-3y(不等式的基本性质3).
∴2-3x<2-3y(不等式的基本性质2).
课堂小结
不等式的
基本性质
性质1
性质2
性质3
a<b,b<c a<c.
a>b a+c>b+c,a-c>b-c;
a<b a+c<b+c,a-c<b-c.
感谢观看!
第3章 一元一次不等式
3.2 不等式的基本性质
学习目标
1.理解不等式的三个基本性质,并能与等式的基本性质区分.
2.会用不等式的基本性质进行简单的不等式变形.
复习回顾
文字语言 符号语言
性质1
性质2
问题:等式有哪些性质?分别用文字语言和符号语言表示.
等式两边加(或减)同一个数(或式子),所得结果仍是等式
等式两边都乘以(或都除以)同一个数(除数不能为0),所得结果仍是等式
如果a=b,
那么a±c=b±c
情境引入
对于左图中的问题,你认为ac是大于bc,还是小于bc?
用几个具体的例子试试看.
猜测:ac<bc.
举例:a=4,b=2,c=-3,则ac=-12,bc=-6,那么ac<bc;
a=8,b=1,c=-5,则ac=-40,bc=-5,那么ac<bc.
…
合作探究
(1)已知a<b和b<c,在数轴上表示如图所示:
a
b
c
由数轴上a和c的位置关系,你能得出什么结论?
你能举几个具体的例子说明吗?
根据a和c的位置关系,可得出a<c.
小组合作,举出几个具体例子对此结论进行说明.
不等式的基本性质1
一
不等式的基本性质 1
a<b,b<c
这个性质也叫做不等式的传递性.
a<c.
b
a
(2)若a>b,则a+c与b+c哪个较大?a-c与b-c呢?请分别用
数轴上点的位置关系和具体的例子加以说明.
a>b,在数轴上表示如图:
b
a
不妨设c>0,则
b
a
c
c
b+c
a+c
可知a+c>b+c.
c
c
b-c
a-c
可知a-c>b-c.
小组合作,举出具体例子加以说明.
思考:若a<b,(2)中的问题又能得到什么结论?
不等式的两边都加上(或减去)同一个数,
所得到的不等式仍成立.
a>b
a<b
不等式的基本性质2
二
不等式的基本性质 2
a+c>b+c,a-c>b-c;
a+c<b+c,a-c<b-c.
现在我们来考虑不等式的两边都乘(或都除以)同一个不为零的数的情况.
成立
若两边都乘-5(或除以-5)呢?
>
>
小组合作,再举几个例子试一试,能得出什么结论?
不等式的两边都乘(或都除以)同一个正数,所得的不等式仍成立;不等式的两边都乘(或都除以)同一个负数,必须改变不等号的方向,所得的不等式成立.
a>b,且c>0
a>b,且c<0
不等式的基本性质3
三
不等式的基本性质 3
例题讲解
例 已知a<0,试比较2a与a的大小.
分析:比较2a与a的大小,可以利用不等式的基本性质,也可以利用数轴,直接得出2a与a的大小.
解法一:∵2>1,a<0,(已知),
∴2a<a(不等式的基本性质3).
例题讲解
例 已知a<0,试比较2a与a的大小.
解法二:在数轴上分别标出表示2a和a的点(a<0),如图所示:
0
a
2a
2a位于a的左边,∴2a<a.
还有其他比较2a与a的大小的方法吗?
想一想
解法三:∵2a-a=a,又∵a<0,
∴2a-a<0,
∴2a<a(不等式的基本性质2).
随堂练习
1. (1)如果x<0.3,而0.3<1,那么x____1;
(2)如果a<3,而b>3,那么a_____b.
解析:(1)根据不等式的传递性可知,x<1.
(2)根据不等式的传递性可知,a<b.
<
<
2.下列说法正确的是( )
A.∵a<b,∴a+2<b+1 B.∵a<b,∴a-1<b-2
C.∵a>b,∴a+c>b+c D.∵a>b,∴a+c>b-d
C
3.由a-3<b+1,可得到结论( )
A.a<b B.a+3<b-1
C.a-1<b+3 D.a+1<b-3
C
4.若x>y,比较2-3x与2-3y的大小,并说明理由.
解:
∵x>y(已知),
∴-3x<-3y(不等式的基本性质3).
∴2-3x<2-3y(不等式的基本性质2).
课堂小结
不等式的
基本性质
性质1
性质2
性质3
a<b,b<c a<c.
a>b a+c>b+c,a-c>b-c;
a<b a+c<b+c,a-c<b-c.
感谢观看!
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
