浙教版八年级上全等模型专题2——一线三等角(K字)模型(含解析)
文档属性
| 名称 | 浙教版八年级上全等模型专题2——一线三等角(K字)模型(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-07 20:10:12 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
全等模型专题2——一线三等角(K字)模型
全等三角形在中考数学几何模块中占据着重要地位,也是学生必须掌握的一块内容,本专题就全等三角形中的重要模型(一线三等角(K字)模型)进行梳理及对应试题分析,方便掌握。
模型1.一线三等角(K型图)模型(同侧型)
【模型解读】
在某条直线上有三个角相等,利用平角为180°与三角形内角和为180°,证得两个三角形全等。
【常见模型及证法】
同侧型一线三等角(常见):
锐角一线三等角 直角一线三等角(“K型图”) 钝角一线三等角
条件:+ CE=DE
证明思路:+任一边相等
例1.(1)如图1,已知:在中,,直线m经过点A,直线m,直线m,垂足分别为点D、E.证明:.
(2)如图2,将(1)中的条件改为:在△ABC中,,D、A、E三点都在直线m上,并且有,其中为任意钝角,请问结论是否成立?如成立,请你给出证明;若不成立,请说明理由.
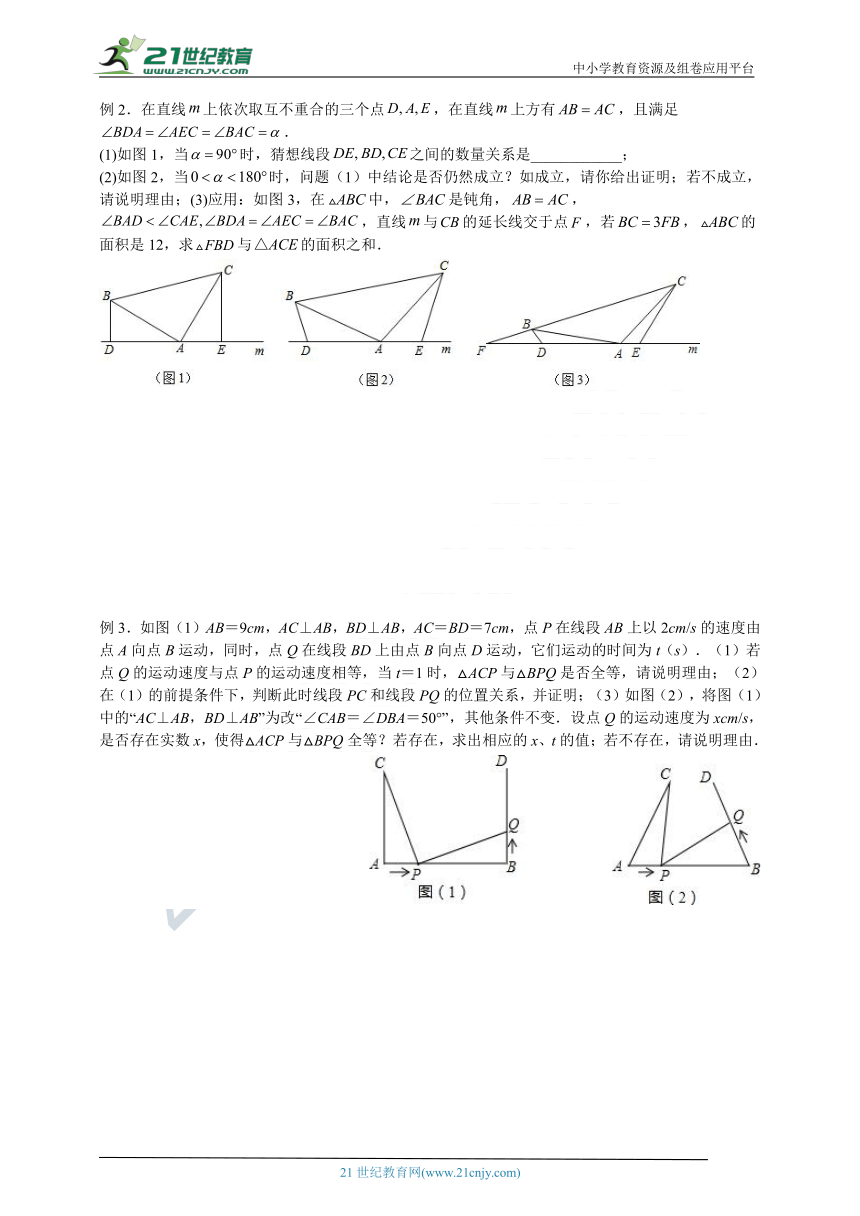
例2.在直线上依次取互不重合的三个点,在直线上方有,且满足.
(1)如图1,当时,猜想线段之间的数量关系是____________;
(2)如图2,当时,问题(1)中结论是否仍然成立?如成立,请你给出证明;若不成立,请说明理由;(3)应用:如图3,在中,是钝角,,,直线与的延长线交于点,若,的面积是12,求与的面积之和.
例3.如图(1)AB=9cm,AC⊥AB,BD⊥AB,AC=BD=7cm,点P在线段AB上以2cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动,它们运动的时间为t(s).(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由;(2)在(1)的前提条件下,判断此时线段PC和线段PQ的位置关系,并证明;(3)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=50°”,其他条件不变.设点Q的运动速度为xcm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
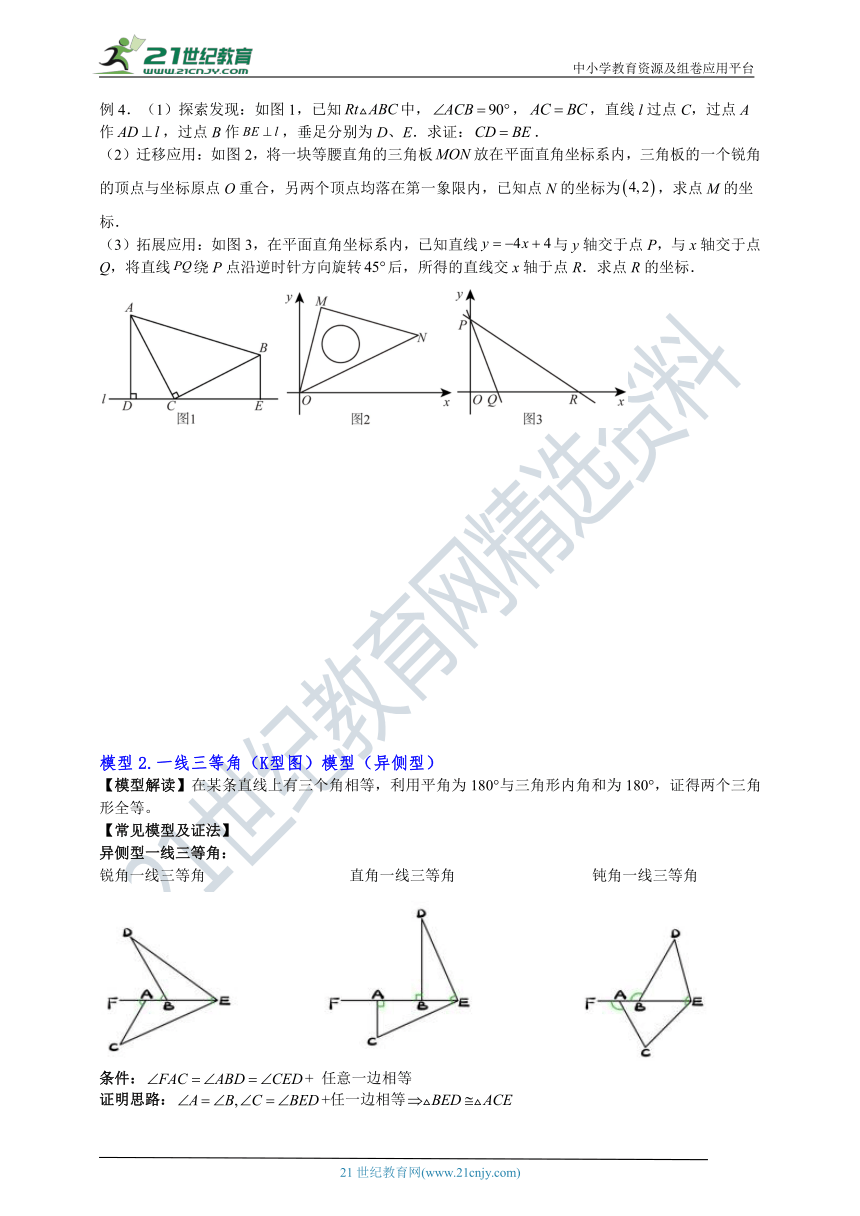
例4.(1)探索发现:如图1,已知中,,,直线l过点C,过点A作,过点B作,垂足分别为D、E.求证:.
(2)迁移应用:如图2,将一块等腰直角的三角板放在平面直角坐标系内,三角板的一个锐角的顶点与坐标原点O重合,另两个顶点均落在第一象限内,已知点N的坐标为,求点M的坐标.
(3)拓展应用:如图3,在平面直角坐标系内,已知直线与y轴交于点P,与x轴交于点Q,将直线绕P点沿逆时针方向旋转后,所得的直线交x轴于点R.求点R的坐标.
模型2.一线三等角(K型图)模型(异侧型)
【模型解读】在某条直线上有三个角相等,利用平角为180°与三角形内角和为180°,证得两个三角形全等。
【常见模型及证法】
异侧型一线三等角:
锐角一线三等角 直角一线三等角 钝角一线三等角
条件:+ 任意一边相等
证明思路:+任一边相等
例1.老师在上课时,在黑板上写了一道题:
“如图,ABCD是正方形,点E在BC上,DF⊥AE于F,请问图中是否存在一组全等三角形?”
小杰同学经过思考发现:△ADF≌△EAB.
理由如下:因为ABCD是正方形(已知)所以∠B=90°且AD=AB和AD∥BC
又因为DF⊥AE(已知)即∠DFA=90°(垂直的意义)
所以∠DFA=∠B(等量代换)
又AD∥BC 所以∠1=∠2(两直线平行,内错角相等)
在△ADF和△EAB中所以△ADF≌△EAB(AAS)
小胖却说这题是错误的,这两个三角形根本不全等.
你知道小杰的错误原因是什么吗?我们再添加一条线段,就能找到与△ADF全等的三角形,请能说出此线段的做法吗?并说明理由.
例2.(1)课本习题回放:“如图①,,,,,垂足分别为,,,.求的长”,请直接写出此题答案:的长为________.
(2)探索证明:如图②,点,在的边、上,,点,在内部的射线上,且.求证:.
(3)拓展应用:如图③,在中,,.点在边上,,点、在线段上,.若的面积为15,则与的面积之和为________.(直接填写结果,不需要写解答过程)
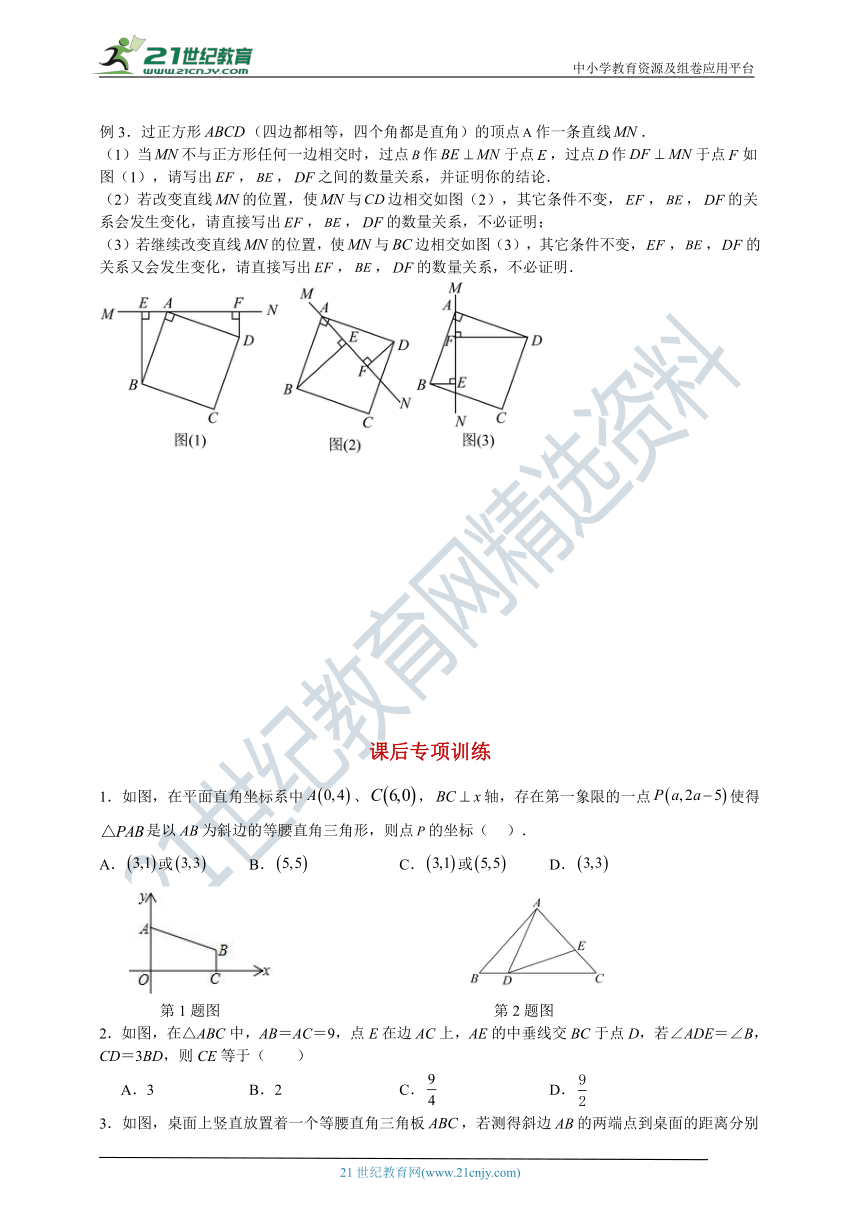
例3.过正方形(四边都相等,四个角都是直角)的顶点作一条直线.
(1)当不与正方形任何一边相交时,过点作于点,过点作于点如图(1),请写出,,之间的数量关系,并证明你的结论.
(2)若改变直线的位置,使与边相交如图(2),其它条件不变,,,的关系会发生变化,请直接写出,,的数量关系,不必证明;
(3)若继续改变直线的位置,使与边相交如图(3),其它条件不变,,,的关系又会发生变化,请直接写出,,的数量关系,不必证明.
课后专项训练
1.如图,在平面直角坐标系中、,轴,存在第一象限的一点使得是以为斜边的等腰直角三角形,则点的坐标( ).
A.或 B. C.或 D.
第1题图 第2题图
2.如图,在△ABC中,AB=AC=9,点E在边AC上,AE的中垂线交BC于点D,若∠ADE=∠B,CD=3BD,则CE等于( )
A.3 B.2 C. D.
3.如图,桌面上竖直放置着一个等腰直角三角板,若测得斜边的两端点到桌面的距离分别为,.(1)求证:;(2)若,,求的长.
4.(1)【问题发现】如图1,△ABC与△CDE中,∠B=∠E=∠ACD=90°,AC=CD,B、C、E三点在同一直线上,AB=3,ED=4,则BE=_____.
(2)【问题提出】如图2,在Rt△ABC中,∠ABC=90°,BC=4,过点C作CD⊥AC,且CD=AC,求△BCD的面积.(3)【问题解决】如图3,四边形ABCD中,∠ABC=∠CAB=∠ADC=45°,△ACD面积为12且CD的长为6,求△BCD的面积.
5.在一次课题学习活动中,老师提出了如下问题:如图,四边形是正方形,点是边的中点,,且交正方形外角平分线于点.请你探究与存在怎样的数量关系,并证明你的结论正确.经过探究,小明得出的结论是,而要证明结论,就需要证明和所在的两个三角形全等,但和显然不全等(一个是直角三角形,一个是钝角三角形),考虑到点是边的中点,小明想到的方法是如图2,取的中点,连接,证明.从而得到.请你参考小明的方法解决下列问题.
(1)如图3,若把条件“点是边的中点”改为“点是边上的任意一点”,其余条件不变,证明结论仍然成立;(2)如图4,若把条件“点是边的中点”改为:“点是边延长线上的一点”,其余条件仍不变,那么结论是否还成立?若成立,请完成证明过程,若不成立,请说明理由.
6.平面内有一等腰直角三角板(∠ACB=90°)和一直线MN.过点C作CE⊥MN于点E,过点B作BF⊥MN于点F.当点E与点A重合时(如图1),易证:AF+BF=2CE.
(1)当三角板绕点A顺时针旋转至图2的位置时,上述结论是否仍然成立?若成立,请给予证明;若不成立,线段AF、BF、CE之间又有怎样的数量关系,请直接写出你的猜想,不需证明.
(2)当三角板绕点A顺时针旋转至图3的位置时,上述结论是否仍然成立?若成立,请给予证明;若不成立,线段AF、BF、CE之间又有怎样的数量关系,请直接写出你的猜想,不需证明.
7.如图1,在中,,,直线经过点,且于,于.(1)由图1,证明:;
(2)当直线绕点旋转到图2的位置时,请猜想出,,的等量关系并说明理由;
(3)当直线绕点旋转到图3的位置时,试问,,又具有怎样的等量关系?请直接写出这个等量关系(不必说明理由).
8.【初步探究】
(1)如图1,在四边形中,,E是边上一点,,连接.请判断的形状,并说明理由.
【问题解决】(2)若设,试利用图1验证勾股定理.
【拓展应用】(3)如图2,在平面直角坐标系中,已知点,点,点C在第一象限内,若为等腰直角三角形,求点C的坐标.
9.通过对下面数学模型的研究学习,解决下列问题:
【模型呈现】(1)如图,,,过点作于点,过点作于点.由,得.又,可以推理得到.进而得到___________,___________.我们把这个数学模型称为“字”模型或“一线三等角”模型;
【模型应用】(2)①如图,,,,连接,,且于点,与直线交于点.求证:点是的中点;②如图,在平面直角坐标系中,点的坐标为,点为平面内任一点.若是以为斜边的等腰直角三角形,请直接写出点的坐标.
10.通过对数学模型“K字”模型或“一线三等角”模型的研究学习,解决下列问题:
[模型呈现]如图1,,,过点B作于点C,过点D作于点E.求证:.
[模型应用]如图2,且,且,请按照图中所标注的数据,计算图中实线所围成的图形的面积为________________.
[深入探究]如图3,,,,连接,,且于点F,与直线交于点G.若,,则的面积为_____________.
11.在中,,,为直线上一点,连接,过点作交于点,交于点,在直线上截取,连接.
(1)当点,都在线段上时,如图①,求证:;
(2)当点在线段的延长线上,点在线段的延长线上时,如图②;当点在线段的延长线上,点在线段的延长线上时,如图③,直接写出线段,,之间的数量关系,不需要证明.
12.(1)如图,等腰直角中,,,线段经过点,过A作于点,过作于求证:≌.
(2)如图,已知在平面直角坐标系中,为坐标原点,点的坐标为,点的坐标为,点是平面直角坐标系中的一点,若是以为直角边的等腰直角三角形,求点的坐标;
(3)如图,已知在平面直角坐标系中,为坐标原点,在等腰直角中,,,点在线段上从向运动运动到点停止,以点为直角顶点向右上方做等腰直角,求点移动的距离.
13.已知:CD是经过∠BCA的顶点C的一条直线,CA=CB,E、F是直线CD上两点,∠BEC=∠CFA=∠α.
(1)若直线CD经过∠BCA的内部,∠BCD>∠ACD.
①如图1,∠BCA=90°,∠α=90°,写出BE,EF,AF间的等量关系: .
②如图2,∠α与∠BCA具有怎样的数量关系,能使①中的结论仍然成立?写出∠α与∠BCA的数量关系 .
(2)如图3.若直线CD经过∠BCA的外部,∠α=∠BCA,①中的结论是否成立?若成立,进行证明;若不成立,写出新结论并进行证明.
14.如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(点D不与点B、C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.
(1)当∠BDA=105°时,∠EDC= °,∠DEC= °;点D从点B向点C运动时,∠BDA逐渐变 .(填“大”或“小”)。(2)当DC等于多少时,△ABD≌△DCE?请说明理由.
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数;若不可以,请说明理由.
15.如图,等腰直角△ABC中,BC=AC,∠ACB=90°,现将该三角形放置在平面直角坐标系中,点B坐标为(0,2),点C坐标为(6,0).
(1)过点A作AD⊥x轴,求OD的长及点A的坐标;
(2)连接OA,若Р为坐标平面内不同于点A的点,且以O、P、C为顶点的三角形与△OAC全等,请直接写出满足条件的点P的坐标;
(3)已知OA=10,试探究在x轴上是否存在点Q,使△OAQ是以OA为腰的等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
八年级全等模型专题2——一线三等角(K字)模型
全等三角形在中考数学几何模块中占据着重要地位,也是学生必须掌握的一块内容,本专题就全等三角形中的重要模型(一线三等角(K字)模型)进行梳理及对应试题分析,方便掌握。
模型1.一线三等角(K型图)模型(同侧型)
【模型解读】
在某条直线上有三个角相等,利用平角为180°与三角形内角和为180°,证得两个三角形全等。
【常见模型及证法】
同侧型一线三等角(常见):
锐角一线三等角 直角一线三等角(“K型图”) 钝角一线三等角
条件:+ CE=DE
证明思路:+任一边相等
例1.(2023·浙江·八年级假期作业)(1)如图1,已知:在中,,直线m经过点A,直线m,直线m,垂足分别为点D、E.证明:.
(2)如图2,将(1)中的条件改为:在△ABC中,,D、A、E三点都在直线m上,并且有,其中为任意钝角,请问结论是否成立?如成立,请你给出证明;若不成立,请说明理由.
【答案】(1)见解析;(2)成立,见解析
【分析】(1)根据可证明,可得,可得.
(2)由已知条件可知,,可得,结合条件可证明,同(1)可得出结论.
【详解】证明:(1)如图1,
∵直线m,直线m,∴,
∵,∴,
∵,∴,
在和中,∴,
∴,∴;
(2)如图2,
∵,∴,∴,
在和中,∴,
∴,∴.
【点睛】本题主要考查了全等三角形的判定和性质,由条件证明三角形全等得到是解题的关键.
例2.(2023春·上海·七年级专题练习)在直线上依次取互不重合的三个点,在直线上方有,且满足.
(1)如图1,当时,猜想线段之间的数量关系是____________;
(2)如图2,当时,问题(1)中结论是否仍然成立?如成立,请你给出证明;若不成立,请说明理由;(3)应用:如图3,在中,是钝角,,,直线与的延长线交于点,若,的面积是12,求与的面积之和.
【答案】(1)DE=BD+CE(2)DE=BD+CE仍然成立,理由见解析(3)△FBD与△ACE的面积之和为4
【分析】(1)由∠BDA=∠BAC=∠AEC=90°得到∠BAD+∠EAC=∠BAD+∠DBA=90°,进而得到∠DBA=∠EAC,然后结合AB=AC得证△DBA≌△EAC,最后得到DE=BD+CE;
(2)由∠BDA=∠BAC=∠AEC=α得到∠BAD+∠EAC=∠BAD+∠DBA=180°﹣α,进而得到∠DBA=∠EAC,然后结合AB=AC得证△DBA≌△EAC,最后得到DE=BD+CE;
(3)由∠BAD>∠CAE,∠BDA=∠AEC=∠BAC,得出∠CAE=∠ABD,由AAS证得△ADB≌△CAE,得出S△ABD=S△CEA,再由不同底等高的两个三角形的面积之比等于底的比,得出S△ABF即可得出结果.
【详解】(1)解:DE=BD+CE,理由如下,∵∠BDA=∠BAC=∠AEC=90°,
∴∠BAD+∠EAC=∠BAD+∠DBA=90°,∴∠DBA=∠EAC,
∵AB=AC,∴△DBA≌△EAC(AAS),∴AD=CE,BD=AE,
∴DE=AD+AE=BD+CE,故答案为:DE=BD+CE.
(2)DE=BD+CE仍然成立,理由如下,∵∠BDA=∠BAC=∠AEC=α,
∴∠BAD+∠EAC=∠BAD+∠DBA=180°﹣α,∴∠DBA=∠EAC,
∵AB=AC,∴△DBA≌△EAC(AAS),
∴BD=AE,AD=CE,∴DE=AD+AE=BD+CE;
(3)解:∵∠BAD<∠CAE,∠BDA=∠AEC=∠BAC,∴∠CAE=∠ABD,
在△ABD和△CAE中,,∴△ABD≌△CAE(AAS),∴S△ABD=S△CAE,
设△ABC的底边BC上的高为h,则△ABF的底边BF上的高为h,
∴S△ABC=BC h=12,S△ABF=BF h,∵BC=3BF,∴S△ABF=4,
∵S△ABF=S△BDF+S△ABD=S△FBD+S△ACE=4,∴△FBD与△ACE的面积之和为4.
【点睛】本题考查了全等三角形的判定与性质、直角三角形的性质,三角形的面积,解题的关键是熟练掌握全等三角形的判定与性质.
例3.(2022春·广东梅州·七年级校考阶段练习)如图(1)AB=9cm,AC⊥AB,BD⊥AB,AC=BD=7cm,点P在线段AB上以2cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动,它们运动的时间为t(s).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由;
(2)在(1)的前提条件下,判断此时线段PC和线段PQ的位置关系,并证明;
(3)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=50°”,其他条件不变.设点Q的运动速度为xcm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
【答案】(1)△ACP与△BPQ全等,理由见解析;(2)PC⊥PQ,证明见解析;(3)存在,当t=1s,x=2cm/s或t=s,x=cm/s时,△ACP与△BPQ全等.
【分析】(1)利用定理证明;(2)根据全等三角形的性质判断线段和线段的位置关系;(3)分,两种情况,根据全等三角形的性质列式计算.
【详解】(1)△ACP与△BPQ全等,
理由如下:当t=1时,AP=BQ=2,则BP=9﹣2=7,∴BP=AC,又∵∠A=∠B=90°,
在△ACP和△BPQ中,,∴△ACP≌△BPQ(SAS);
(2)PC⊥PQ,证明:∵△ACP≌△BPQ,∴∠ACP=∠BPQ,
∴∠APC+∠BPQ=∠APC+∠ACP=90°.∴∠CPQ=90°,即线段PC与线段PQ垂直;
(3)①若△ACP≌△BPQ,则AC=BP,AP=BQ,
∴9﹣2t=7,解得,t=1(s),则x=2(cm/s);
②若△ACP≌△BQP,则AC=BQ,AP=BP,则2t=×9,
解得,t=(s),则x=7÷=(cm/s),
故当t=1s,x=2cm/s或t=s,x=cm/s时,△ACP与△BPQ全等.
【点睛】本题考查的是全等三角形的判定与性质,掌握全等三角形的判定定理和性质定理、注意分
类讨论思想的灵活运用是解题的关键.
例4.(2022·贵州铜仁·三模)(1)探索发现:如图1,已知中,,,直线l过点C,过点A作,过点B作,垂足分别为D、E.求证:.
(2)迁移应用:如图2,将一块等腰直角的三角板放在平面直角坐标系内,三角板的一个锐角的顶点与坐标原点O重合,另两个顶点均落在第一象限内,已知点N的坐标为,求点M的坐标.
(3)拓展应用:如图3,在平面直角坐标系内,已知直线与y轴交于点P,与x轴交于点Q,将直线绕P点沿逆时针方向旋转后,所得的直线交x轴于点R.求点R的坐标.
【答案】(1)见详解;(2)点M的坐标为(1,3);(3)R(,0)
【分析】(1)先判断出∠ACB=∠ADC,再判断出∠CAD=∠BCE,进而判断出△ACD≌△CBE,即可得出结论;(2)过点M作MF⊥y轴,垂足为F,过点N作NG⊥MF,判断出MF=NG,OF=MG,设M(m,n)列方程组求解,即可得出结论;(3)过点Q作QS⊥PQ,交PR于S,过点S作SH⊥x轴于H,先求出OP=4,由y=0得x=1,进而得出Q(1,0),OQ=1,再判断出PQ=SQ,即可判断出OH=5,SH=OQ=1,进而求出直线PR的解析式,即可得出结论.
【详解】(1)证明:∵∠ACB=90°,AD⊥l,∴∠ACB=∠ADC.
∵∠ACE=∠ADC+∠CAD,∠ACE=∠ACB+∠BCE,∴∠CAD=∠BCE,
∵∠ADC=∠CEB=90°,AC=BC.∴△ACD≌△CBE,∴CD=BE,
(2)解:如图2,过点M作MF⊥y轴,垂足为F,过点N作NG⊥MF,交FM的延长线于G,
由已知得OM=ON,且∠OMN=90°,∴由(1)得△OFM≌△MGN,
∴MF=NG,OF=MG,设M(m,n),∴MF=m,OF=n,∴MG=n,NG=m,
∵点N的坐标为(4,2)∴解得∴点M的坐标为(1,3);
(3)如图3,过点Q作QS⊥PQ,交PR于S,过点S作SH⊥x轴于H,
对于直线y=﹣4x+4,由x=0得y=4,
∴P(0,4),∴OP=4,由y=0得x=1,∴Q(1,0),OQ=1,
∵∠QPR=45°,∴∠PSQ=45°=∠QPS.∴PQ=SQ.∴由(1)得SH=OQ,QH=OP.
∴OH=OQ+QH=OQ+OP=4+1=5,SH=OQ=1.∴S(5,1),
设直线PR为y=kx+b,则,解得.∴直线PR为y=x+4.
由y=0得,x=,∴R(,0).
【点睛】本题是一次函数综合题,主要考查了待定系数法,全等三角形的判定和性质,构造出全等三角形是解本题的关键.
模型2.一线三等角(K型图)模型(异侧型)
【模型解读】在某条直线上有三个角相等,利用平角为180°与三角形内角和为180°,证得两个三角形全等。
【常见模型及证法】
异侧型一线三等角:
锐角一线三等角 直角一线三等角 钝角一线三等角
条件:+ 任意一边相等
证明思路:+任一边相等
例1.(2022·浙江杭州·一模)老师在上课时,在黑板上写了一道题:
“如图,ABCD是正方形,点E在BC上,DF⊥AE于F,请问图中是否存在一组全等三角形?”
小杰同学经过思考发现:△ADF≌△EAB.
理由如下:因为ABCD是正方形(已知)所以∠B=90°且AD=AB和AD∥BC
又因为DF⊥AE(已知)即∠DFA=90°(垂直的意义)
所以∠DFA=∠B(等量代换)
又AD∥BC 所以∠1=∠2(两直线平行,内错角相等)
在△ADF和△EAB中所以△ADF≌△EAB(AAS)
小胖却说这题是错误的,这两个三角形根本不全等.
你知道小杰的错误原因是什么吗?我们再添加一条线段,就能找到与△ADF全等的三角形,请能说出此线段的做法吗?并说明理由.
【答案】小杰错误的原因是AD和AB不是对应边,在证明两个三角形全等时,误以为对应边了;线段为作BH⊥AE于点H,证明见详解;
【分析】根据小杰的证明方法,可以发现,在证明两个三角形全等时,出现了问题,然后说出出错的原因即可,然后添加合适的辅助线段,说明与△ADF全等的三角形成立的理由即可解答本题;
【详解】小杰错误的原因是AD和AB不是对应边,在证明两个三角形全等时,误以为对应边了,作BH⊥AE于H,则△ADF≌△BAH;
∵四边形ABCD是正方形,∴AD=BA,∠DAB=90°,∴∠HAB+∠FAD=90°,
∵DF⊥AE,BH⊥AE,∴∠DFA=∠AHB=90°,
∴∠HAB+∠HBA=90°,∴∠FAD=∠HBA,
在△ADF和△BAH中 ∴△ADF≌△BAH(AAS);
【点睛】本题考查正方形的性质、全等三角形的判定,解答本题的关键是明确题意,利用数形结合的思想解答;
例2.(2022·山东·九年级课时练习)(1)课本习题回放:“如图①,,,,,垂足分别为,,,.求的长”,请直接写出此题答案:的长为________.
(2)探索证明:如图②,点,在的边、上,,点,在内部的射线上,且.求证:.
(3)拓展应用:如图③,在中,,.点在边上,,点、在线段上,.若的面积为15,则与的面积之和为________.(直接填写结果,不需要写解答过程)
【答案】(1)0.8cm;(2)见解析(3)5
【分析】(1)利用AAS定理证明△CEB≌△ADC,根据全等三角形的性质解答即可;
(2)由条件可得∠BEA=∠AFC,∠4=∠ABE,根据AAS可证明△ABE≌△CAF;
(3)先证明△ABE≌△CAF,得到与的面积之和为△ABD的面积,再根据故可求解.
【详解】解:(1)∵BE⊥CE,AD⊥CE,∴∠E=∠ADC=90°,∴∠EBC+∠BCE=90°.
∵∠BCE+∠ACD=90°,∴∠EBC=∠DCA.在△CEB和△ADC中,
∴△CEB≌△ADC(AAS),∴BE=DC,CE=AD=2.5cm.
∵DC=CE DE,DE=1.7cm,∴DC=2.5 1.7=0.8cm,∴BE=0.8cm故答案为:0.8cm;
(2)证明:∵∠1=∠2,∴∠BEA=∠AFC.
∵∠1=∠ABE+∠3,∠3+∠4=∠BAC,∠1=∠BAC,
∴∠BAC=∠ABE+∠3,∴∠4=∠ABE.
∵∠AEB=∠AFC,∠ABE=∠4,AB=AC,∴△ABE≌△CAF(AAS).
(3)∵∴∠ABE+∠BAE=∠FAC+∠BAE=∠FAC+∠ACF
∴∠ABE=∠CAF,∠BAE=∠ACF 又∴△ABE≌△CAF,∴
∴与的面积之和等于与的面积之和,即为△ABD的面积,
∵,△ABD与△ACD的高相同则=5
故与的面积之和为5故答案为:5.
【点睛】本题考查的是全等三角形的判定和性质、三角形内角和定理,掌握全等三角形的判定定理和性质定理是解题的关键.
例3.(2023·贵州遵义·八年级统考期末)过正方形(四边都相等,四个角都是直角)的顶点作一条直线.
(1)当不与正方形任何一边相交时,过点作于点,过点作于点如图(1),请写出,,之间的数量关系,并证明你的结论.
(2)若改变直线的位置,使与边相交如图(2),其它条件不变,,,的关系会发生变化,请直接写出,,的数量关系,不必证明;
(3)若继续改变直线的位置,使与边相交如图(3),其它条件不变,,,的关系又会发生变化,请直接写出,,的数量关系,不必证明.
【答案】(1),证明见解析;(2);(3)
【分析】(1)根据同角的余角相等可证,再证,根据全等三角形的对应边相等进行代换即可;(2)根据同角的余角相等可证,再证,根据全等三角形的对应边相等进行代换即可;(3)根据同角的余角相等可证,再证,根据全等三角形的对应边相等进行代换即可.
【详解】(1),证明:
四边形是正方形,
又, ∴
在和中
,
(2),理由是:四边形是正方形 ,
又, ∴
在和中
, ∴EF=AF-AE=BE-DF
(3),理由是:
四边形是正方形,
又, ∴
在和中
, EF=AE-AF=DF-BE
【点睛】本题考查的是三角形全等的判定和性质,掌握三角形的判定方法及能利用同角的余角相等证明是关键.
课后专项训练
1.(2022·贵州·凯里一模)如图,在平面直角坐标系中、,轴,存在第一象限的一点使得是以为斜边的等腰直角三角形,则点的坐标( ).
A.或 B. C.或 D.
【答案】C
【分析】分点P在AB的上方和点P在AB的下方,根据全等三角形的判定与性质进行讨论求解即可.
【详解】解:当点P在AB的上方时,过P作x轴的平行线交y轴于E,交CB延长线于F,如图1,
则∠AEP=∠PFB=∠APB=90°,E(0,2a﹣5),F(6,2a﹣5),∴PE=a,PF=6﹣a,AE=2a﹣9,
∵∠EAP+∠EPA=90°,∠EPA+∠BPF=90°,∴∠EAP=∠BPF,又∠AEP=∠PFB,PA=PB,
∴△AEP≌△PFB(AAS),∴AE=PF,∴6﹣a=2a﹣9,解得:a=5,∴P(5,5);
当点P在AB的下方时,同样过P作x轴的平行线交y轴于E,交CB于F,如图2,
则∠AEP=∠PFB=∠APB=90°,E(0,2a﹣5),F(6,2a﹣5),∴PE=a,PF=6﹣a,AE=9﹣2a,
∵∠EAP+∠EPA=90°,∠EPA+∠BPF=90°,∴∠EAP=∠BPF,又∠AEP=∠PFB,PA=PB,
∴△AEP≌△PFB(AAS),∴AE=PF,∴9﹣2a=6﹣a,解得:a=3,∴P(3,1),
综上,点P的坐标为(3,1)或(5,5),故选:C.
【点睛】本题考查等腰直角三角形的性质、全等三角形的判定与性质、等角的余角相等、坐标与图形性质、解一元一次方程等知识,过已知点向坐标轴作平行线或垂线,然后求出相关线段的长是解决此类问题的基本方法.
2.(2023·浙江·八年级假期作业)如图,在△ABC中,AB=AC=9,点E在边AC上,AE的中垂线交BC于点D,若∠ADE=∠B,CD=3BD,则CE等于( )
A.3 B.2 C. D.
【答案】A
【分析】根据等腰三角形的性质得到∠B=∠C,推出∠BAD=∠CDE,根据线段垂直平分线的性质得到AD=ED,根据全等三角形的性质得到CD=AB=9,BD=CE,即可得到结论.
【详解】解:∵AB=AC=9,∴∠B=∠C,
∵∠ADE=∠B,∠BAD=180°﹣∠B﹣∠ADB,∠CDE=180°﹣∠ADE﹣∠ADB,
∴∠BAD=∠CDE,∵AE的中垂线交BC于点D,∴AD=ED,
在△ABD与△DCE中,,
∴△ABD≌△DCE(AAS),∴CD=AB=9,BD=CE,
∵CD=3BD,∴CE=BD=3故选:A.
【点睛】本题考查了等腰三角形的性质,线段垂直平分线的性质,全等三角形的性质,属于基础题.
3.(2022·河北保定·模拟预测)如图,桌面上竖直放置着一个等腰直角三角板,若测得斜边的两端点到桌面的距离分别为,.(1)求证:;(2)若,,求的长.
【答案】(1)见解析;(2)3
【分析】(1)先利用同角的余角相等,判断出∠DAC=∠BCE,进而判断出△ACD≌△CBE;
(2)由全等三角形的性质,即可求出答案.
【详解】解:(1)证明:∵,,
∴,∴.
∵,∴,∴,
∴.∴
(2)解:∵,∴,.∵,∴,
∵,∴,∴.
【点睛】此题主要考查了等腰直角三角形的性质,全等三角形的判定和性质,判断出△ACD≌△CBE是解本题的关键.
4.(1)【问题发现】如图1,△ABC与△CDE中,∠B=∠E=∠ACD=90°,AC=CD,B、C、E三点在同一直线上,AB=3,ED=4,则BE=_____.
(2)【问题提出】如图2,在Rt△ABC中,∠ABC=90°,BC=4,过点C作CD⊥AC,且CD=AC,求△BCD的面积.(3)【问题解决】如图3,四边形ABCD中,∠ABC=∠CAB=∠ADC=45°,△ACD面积为12且CD的长为6,求△BCD的面积.
【答案】(1)7;(2)S△BCD=8;(3)S△BCD=6.
【分析】(1) ∠B=∠E=∠ACD=90°,根据同角的余角相等,可得∠ACB=∠D,由已知条件可证△ABC≌△CED,可得答案;
(2)过D作DE⊥BC交BC延长线于E,同(1)中的方法,可证△ABC≌△CED,可得答案;
(3)过A作AE⊥CD于E,过B作BF⊥CD交DC延长线于F,由△ACD面积为12且CD的长为6,可得AE=4,进而可得CE=2,同(1)中证法,可得△ACE≌△CBF,由全等三角形的性质可求得答案.
【详解】解:(1)∵∠ACD=∠E=90°,∴∠ACB=90°﹣∠DCE=∠D,
在△ABC和△CED中,,∴△ABC≌△CED(AAS),
∴AB=CE=3,BC=ED=4,∴BE=BC+CE=7;故答案为:7;
(2)过D作DE⊥BC交BC延长线于E,如图:
∵DE⊥BC,CD⊥AC,∴∠E=∠ACD=90°,∴∠ACB=90°﹣∠DCE=∠CDE,
在△ABC和△CED中,,∴△ABC≌△CED(AAS),
∴BC=ED=4,∴S△BCD=BC DE=8;
(3)过A作AE⊥CD于E,过B作BF⊥CD交DC延长线于F,如图:
∵△ACD面积为12且CD的长为6,∴×6 AE=12,∴AE=4,
∵∠ADC=45°,AE⊥CD,∴△ADE是等腰直角三角形,∴DE=AE=4,∴CE=CD﹣DE=2,
∵∠ABC=∠CAB=45°,∴∠ACB=90°,AC=BC,∴∠ACE=90°﹣∠BCF=∠CBF,
在△ACE和△CBF中,,∴△ACE≌△CBF(AAS),
∴BF=CE=2,∴S△BCD=CD BF=6.
【点睛】本题考查全等三角形的性质与判定,属于类比探究类的题目,掌握模型思想,准确作出辅助线构造全等三角形是解题的关键.
5.在一次课题学习活动中,老师提出了如下问题:如图,四边形是正方形,点是边的中点,,且交正方形外角平分线于点.请你探究与存在怎样的数量关系,并证明你的结论正确.经过探究,小明得出的结论是,而要证明结论,就需要证明和所在的两个三角形全等,但和显然不全等(一个是直角三角形,一个是钝角三角形),考虑到点是边的中点,小明想到的方法是如图2,取的中点,连接,证明.从而得到.请你参考小明的方法解决下列问题.
(1)如图3,若把条件“点是边的中点”改为“点是边上的任意一点”,其余条件不变,证明结论仍然成立;(2)如图4,若把条件“点是边的中点”改为:“点是边延长线上的一点”,其余条件仍不变,那么结论是否还成立?若成立,请完成证明过程,若不成立,请说明理由.
【答案】(1)正确,见解析;(2)正确,见解析
【分析】(1)在AB上取点,连接,证明△PAE≌△CEF即可;
(2)延长BA至,使=CE,连接,证明△ANE≌△ECF即可.
【详解】解:(1)正确.证明:在AB上取一点M,使AM=EC,连接ME.
四边形是正方形,
∴BM=BE,∴∠BME=45°,∴∠AME=135°,
∵CF是外角平分线,∴∠DCF=45°,∴∠ECF=135°,∴∠AME=∠ECF,
∵∠AEB+∠BAE=90°,∠AEB+∠CEF=90°,∴∠BAE=∠CEF,
∴△AME≌△ECF(ASA),∴AE=EF.
(2)正确.证明:在BA的延长线上取一点N.
使AN=CE,连接NE.∴BN=BE,∴∠N=∠NEC=45°,
∵CF平分∠DCG,∴∠FCE=45°,∴∠N=∠ECF,
∵四边形ABCD是正方形,∴AD∥BE,∴∠DAE=∠BEA,
即∠DAE+90°=∠BEA+90°,∴∠NAE=∠CEF,∴△ANE≌△ECF(ASA)∴AE=EF.
【点睛】本题考查的是构造三角形全等证明线段的相等,同时考查了正方形的性质,掌握构造全等三角形是解题关键.
6.平面内有一等腰直角三角板(∠ACB=90°)和一直线MN.过点C作CE⊥MN于点E,过点B作BF⊥MN于点F.当点E与点A重合时(如图1),易证:AF+BF=2CE.
(1)当三角板绕点A顺时针旋转至图2的位置时,上述结论是否仍然成立?若成立,请给予证明;若不成立,线段AF、BF、CE之间又有怎样的数量关系,请直接写出你的猜想,不需证明.
(2)当三角板绕点A顺时针旋转至图3的位置时,上述结论是否仍然成立?若成立,请给予证明;若不成立,线段AF、BF、CE之间又有怎样的数量关系,请直接写出你的猜想,不需证明.
【答案】(1)AF+BF=2CE仍成立 (2)AF-BF=2CE
【分析】(1)过B作BH⊥CE于点H,可证△ACE≌△CBH,通过线段的等量代换可得结论;
(2)过点B作BG⊥CE,交CE的延长线于点G,△ACE≌△CBG,通过线段的等量代换可得答案.
(1)解:图2,AF+BF=2CE仍成立,
证明:如图,过B作BH⊥CE于点H,
∵∠BCH+∠ACE=90°,又∵在直角△ACE中,∠ACE+∠CAE=90°,∴∠CAE=∠BCH,
又∵AC=BC,∠AEC=∠BHC=90°∴△ACE≌△CBH.∴CH=AE,BF=HE,CE=BH,
∴AF+BF=AE+EF+BF=CH+EF+HE=CE+EF=2EC.
(2)解:不成立,线段AF、BF、CE之间的数量关系为:AF-BF=2CE
证明:如图,过点B作BG⊥CE,交CE的延长线于点G,
∵∠BCG+∠ACE=90°,又∵在直角△ACE中,∠ACE+∠CAE=90°,∴∠CAE=∠BCG,
又∵AC=BC,∠AEC=∠BGC=90°∴△ACE≌△CBG.∴CG=AE,BF=GE,CE=BG,
∴AF-BF=AE+EF-BF=CG+EF-GE=CE+EF=2EC.
【点睛】本题考查全等三角形的判定,根据题意正确作出辅助线构造全等三角形是解题的关键.
7.如图1,在中,,,直线经过点,且于,于.(1)由图1,证明:;
(2)当直线绕点旋转到图2的位置时,请猜想出,,的等量关系并说明理由;
(3)当直线绕点旋转到图3的位置时,试问,,又具有怎样的等量关系?请直接写出这个等量关系(不必说明理由).
【答案】(1)证明见解析;(2),证明过程见解析;(3),证明过程见解析
【分析】(1)先证明△ADC≌△CEB,得到AD=CE,DC=BE,进而得到DE=CE+DC=AD+BE即可;
(2)同(1)中思路,证明△ADC≌△CEB,进而得到DE=CE-DC=AD-BE即可;
(3)同(1)中思路,证明△ADC≌△CEB,进而得到DE=DC-CE=BE-AD即可.
【详解】解:(1)证明:在中,∵,∴,
∵,∴,∴,
又∵,,∴,∴,,
∵直线经过点,∴;
(2),,的等量关系为:,理由如下:
∵于,于∴,
∴,,∴,
在和中,∴
∴,,∴;
(3)当旋转到图3的位置时,、、所满足的等量关系是,理由如下:
∵于,于∴,
∴,,∴,
在和中,∴
∴,,∴.
【点睛】本题考查了全等三角形的判定方法、等腰直角三角形的性质及等角的余角相等等知识点,熟练掌握三角形全等的判定方法是求解的关键.
8.(2023春·浙江·八年级期中)【初步探究】
(1)如图1,在四边形中,,E是边上一点,,连接.请判断的形状,并说明理由.
【问题解决】(2)若设,试利用图1验证勾股定理.
【拓展应用】(3)如图2,在平面直角坐标系中,已知点,点,点C在第一象限内,若为等腰直角三角形,求点C的坐标.
【答案】(1)是等腰直角三角形,理由见解析;(2)见解析;(3)点C的坐标为(1,2)或(3,3)或.
【分析】(1)利用全等三角形的判定证明≌,再由全等三角形的性质及直角三角形的性质即可得到结论;(2)利用图形的面积建立等式进行化简即可;
(3)分三种情况,作辅助线构造全等三角形求解即可.
【详解】解:(1)是等腰直角三角形,理由如下:
在和中,,∴≌,∴AE= DE,∠AEB=∠EDC,
∵在中,∠C=90°,∴∠EDC+∠DEC= 90°,∴∠AEB+∠DEC= 90°,
∵∠AEB+∠DEC+∠AED=180°,∴∠AED=90°,∴是等腰直角三角形;
(2)由题可知,四边形ABCD为梯形,
∵≌,,,,∴AB=CE=b,BE=CD=a,
∴,
又∵,
∴,∴,∴;
(3)①当∠CAB=90°,CA=AB时,如图,过点C作CF⊥x轴于点F,过点B作BE⊥x轴于点E,
∵点A(2,0),点B(4,1),∴BE=1,OA=2,OE=4,∴AE= 2,
∵∠CAB=90°,BE⊥x轴,∴∠CAF+∠BAE= 90°,∠BAE+∠ABE=90°,∴∠CAF=∠ABE,
又∵AC= AB,∠AFC=∠AEB=90°,∴≌,
∴CF=AE= 2,AF=BE=1,∴OF=OA-AF=1,∴点C坐标为(1,2);
②当∠ABC=90°,AB=BC时,如图,过点B作BE⊥x轴于点E,过点C作CF⊥BE交EB延长线于点F,
∵∠ABC=90°,BE⊥x轴,∴∠ABE+∠CBF= 90°,∠ABE+∠BAE=90°,∴∠BAE=∠CBF,
又∵BC= AB,∠AEB=∠CFB=90°,∴≌,
∴BE=CF=1,AE=BF= 2,∴EF=3,∴点C坐标为(3,3);
③当∠ACB=90°,CA=BC时,如图,过点C作CD⊥x轴于点D,过点B作BF⊥CD于点F,BE⊥x轴于点E,
∵∠ACB=90°,CD⊥x轴,∴∠ACD+∠BCF=90°,∠ACD+∠CAD=90°,∴∠BCF=∠CAD,
又∵AC= BC,∠CDA=∠BFC=90°,∴≌,∴CF=AD, BF=CD=DE,
∵AD+DE=AE=2,∴2=AD+CD=AD+CF+DF=2AD+1,∴,
∴,,∴点C坐标为,
综上所述,点C的坐标为(1,2)或(3,3)或.
【点睛】本题考查了全等三角形的判定与性质,勾股定理的验证,平面直角坐标系中等腰直角三角形的存在性问题,熟练掌握各性质及判定定理,正确作辅助线构造出全等三角形是解题的关键.
9.通过对下面数学模型的研究学习,解决下列问题:
【模型呈现】(1)如图,,,过点作于点,过点作于点.由,得.又,可以推理得到.进而得到___________,___________.我们把这个数学模型称为“字”模型或“一线三等角”模型;
【模型应用】(2)①如图,,,,连接,,且于点,与直线交于点.求证:点是的中点;②如图,在平面直角坐标系中,点的坐标为,点为平面内任一点.若是以为斜边的等腰直角三角形,请直接写出点的坐标.
【答案】(1);(2)①证明见解析;②或
【分析】(1)根据全等三角形的对应边相等解答;(2)①作于,于,证明,,根据全等三角形的性质得到,再证明,根据全等三角形的性质证明结论;②过点作轴于点,过点作轴于点,两直线交于点,过点作轴于点,交于点,利用(1)的结论即可解答.
【详解】(1)解:∵,∴,
在和中,,∴,
∴,.故答案为:;.
(2)①证明:如图,作于,于,
∵,,∴,∴,
在和中,,∴,∴,
∵,,∴,∴,
在和中,,∴,∴,∴,
∵,,∴,
在和中,∴,∴,∴点是的中点;
②解:如图,和是以为斜边的等腰直角三角形,
∴,,
过点作轴于点,过点作轴于点,两直线交于点,过点作轴于点,交于点,∴,
∵,∴四边形是矩形,∴,,,
∵是以为斜边的等腰直角三角形,∴,,
由(1)可知,,∴,,
∵点的坐标为,∴,,
又∵,∴,
解得:,,∴点的坐标为,
∵,,,由(1)可知,,
∴,,∴点的坐标为.
综上所述,是以为斜边的等腰直角三角形,点B的坐标为或.
【点睛】本题属于三角形综合题,考查全等三角形的判定和性质、坐标与图形性质.掌握全等三角形的判定定理和性质定理是解题的关键.
10.通过对数学模型“K字”模型或“一线三等角”模型的研究学习,解决下列问题:
[模型呈现]如图1,,,过点B作于点C,过点D作于点E.求证:.
[模型应用]如图2,且,且,请按照图中所标注的数据,计算图中实线所围成的图形的面积为________________.
[深入探究]如图3,,,,连接,,且于点F,与直线交于点G.若,,则的面积为_____________.
【答案】[模型呈现]见解析;[模型应用]50;[深入探究]63
【分析】[模型呈现]证明,根据全等三角形的对应边相等得到;
[模型应用]根据全等三角形的性质得到,,,根据梯形的面积公式计算,得到答案;
[深入探究]过点D作于P,过点E作交的延长线于Q,根据全等三角形的性质得到,证明,得到,进而求出,根据三角形的面积公式计算即可.
【详解】[模型呈现]证明:∵,∴,
∵,∴,
∴,∴,
在和中,,∴,∴;
[模型应用]解:由[模型呈现]可知,,
∴,
则,
故答案为:50;
[深入探究]过点D作于P,过点E作交AG的延长线于Q,
由[模型呈现]可知,,
∴,
在和中,,∴,∴,
∵,∴,∴,
∴,∴,故答案为:63.
【点睛】本题考查的是全等三角形的判定和性质、三角形的面积计算,熟记三角形确定的判定定理是解题的关键.
11.在中,,,为直线上一点,连接,过点作交于点,交于点,在直线上截取,连接.
(1)当点,都在线段上时,如图①,求证:;
(2)当点在线段的延长线上,点在线段的延长线上时,如图②;当点在线段的延长线上,点在线段的延长线上时,如图③,直接写出线段,,之间的数量关系,不需要证明.
【答案】(1)见解析;(2)图②:;图③:
【分析】(1)过点作交的延长线于点.证明,根据全等三角形的性质可得,.再证,由此即可证得结论;(2)图②:,类比(1)中的方法证明即可;图③:,类比(1)中的方法证明即可.
【详解】(1)证明:如图,过点作交的延长线于点.
∴.∵,∴,.
∵,∴.∴.
在和中,∴.∴,.
∵,,∴.
∴.∴.
∵,,∴.
在和中,∴.∴.
∵,∴.
(2)图②:.证明:过点作交于点.
∴.∵,∴,.
∵,∴.∴.
在和中,∴.∴,.
∵,,∴.∴,
∵∴.∴.
∵,,∴.
在和中,∴.∴.
∵,∴.
图③:.
证明:如图,过点作交的延长线于点.
∴.∵,∴,.
∵,∴.∴.
在和中,∴.∴,.
∵,,∴.∴.∴.
∵,,∴.
在和中,∴.∴.
∵,∴.
【点睛】本题是全等三角形的综合题,正确作出辅助线,构造全等三角形是解决问题的关键.
12.(1)如图,等腰直角中,,,线段经过点,过A作于点,过作于求证:≌.
(2)如图,已知在平面直角坐标系中,为坐标原点,点的坐标为,点的坐标为,点是平面直角坐标系中的一点,若是以为直角边的等腰直角三角形,求点的坐标;
(3)如图,已知在平面直角坐标系中,为坐标原点,在等腰直角中,,,点在线段上从向运动运动到点停止,以点为直角顶点向右上方做等腰直角,求点移动的距离.
【答案】(1)见解析;(2),,,;(3)8
【分析】(1)根据等腰直角三角形的性质证明即可;(2)分四种情况,由(1)的结论并结合等腰直角三角形的性质即可证明;(3)过点作轴于点,过点作于点,由(1)的结论和等腰直角三角形的性质即可证明.
【详解】解:(1)为等腰直角三角形,,
又,,,,
又,,即,≌;
(2)分四种情况讨论:当点为直角顶点时,且点在左侧时,如图,过点作轴于点.
为等腰直角三角形,由(1)可知:≌,
,,,,
,,,;
其余三种情况如图所示,
同理可求得:,,;
(3)过点作轴于点,过点作于点,如图,
为等腰直角三角形,由(1)可知:≌,
,,,
点在直线上运动,当点在点时,点的坐标是,
当点在点时,点的坐标是,点运动的距离是.
【点睛】本题考查了等腰直角三角形的性质和全等三角形的判定和性质,解决本题的关键是掌握等腰直角三角形的性质.
13.已知:CD是经过∠BCA的顶点C的一条直线,CA=CB,E、F是直线CD上两点,∠BEC=∠CFA=∠α.
(1)若直线CD经过∠BCA的内部,∠BCD>∠ACD.
①如图1,∠BCA=90°,∠α=90°,写出BE,EF,AF间的等量关系: .
②如图2,∠α与∠BCA具有怎样的数量关系,能使①中的结论仍然成立?写出∠α与∠BCA的数量关系 .
(2)如图3.若直线CD经过∠BCA的外部,∠α=∠BCA,①中的结论是否成立?若成立,进行证明;若不成立,写出新结论并进行证明.
【答案】(1)①EF= BE-AF;②∠α+ ∠BCA = 180°,理由见解析;(2)不成立,EF=BE+AF,证明见解析
【分析】(1)①求出∠BEC=∠AFC = 90°, ∠CBE=∠ACF,根据AAS证△BCE≌△CAF,推出BE=CF,CE = AF即可得出结论;②求出∠BEC =∠AFC,∠CBE=∠ACF,根据AAS证△BCE≌△CAF,推出BE= CF,CE = AF即可得出结论;
(2)求出∠BEC =∠AFC,∠CBE= ∠ACF,根据AAS证△BCE≌△CAF,推出BE= CF,CE=AF即可得出结论.
【详解】(1)①EF、BE、AF的数量关系:EF= BE-AF,
证明:当α =90°时,∠BEC = ∠CFA =90°,
∵∠BCA = 90°,
∴∠BCE+∠ACF= 90°,
∵∠BCE+∠CBE =90°,
∴∠ACF = ∠CBE,
∵AC = BC,
∴△BCE≌△CAF,
∴BE =CF,CE = AF,
∵CF =CE+EF,
∴EF= CF -CE=BE-AF;
②∠α与∠BCA关系:∠α+ ∠BCA = 180°
当∠α+ ∠BCA = 180°时,①中结论仍然成立;
理由是:如题图2,
∵∠BEC = ∠CFA = ∠α, ,∠α+∠ACB =180°,
又∵
∴∠CBE= ∠ACF,
在△BCE和△CAF中
∴△BCE≌△CAF (AAS),
∴BE =CF,CE = AF,
∴EF= CF-CE= BE -AF;
故答案为: ∠α+ ∠BCA = 180° ;
(2)EF、BE、AF的数量关系:EF=BE+AF,理由如下
∵∠BEC =∠CFA =∠α, ∠α= ∠BCA,
又∵∠EBC +∠BCE+∠BEC = 180° , ∠BCE+∠ACF+∠ACB =180° ,
∴∠EBC +∠BCE =∠BCE+∠ACF
∴∠EBC = ∠ACF,
在△BEC和△CFA中
∴△ABE≌△CFA(AAS)
∴AF = CE,BE = CF
∵EF= CE+CF,
∴EF= BE+AF.
【点睛】本题考查了全等三角形的性质和判定,证明△BCE≌△CAF是解题的关键.
14.如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(点D不与点B、C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.
(1)当∠BDA=105°时,∠EDC= °,∠DEC= °;点D从点B向点C运动时,∠BDA逐渐变 .(填“大”或“小”)。(2)当DC等于多少时,△ABD≌△DCE?请说明理由.
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数;若不可以,请说明理由.
【答案】(1),小;(2)2,理由见解析;(3)或80°
【分析】(1)根据已知条件, 三角形内角和定理和平角的定义,可得,,进而可得∠EDC,∠DEC,根据题意,可得当点D从点B向点C运动时,逐渐变大,根据三角形内角和定理,即可得∠BDA逐渐变小;
(2)由(1)可得,,只要,即可证明,进而可得;
(3)根据题意,分为顶角和底角两种情况讨论,进而计算的度数.
【详解】(1),,
,
,
,
,
,,
当∠BDA=105°时,
∠EDC=,
∠DEC=;
当点D从点B向点C运动时,逐渐变大,,则∠BDA逐渐变小,
故答案为:,小;
(2),,
当时,
(AAS),
,
(3)△ADE的形状可以是等腰三角形,或,
,
,
①当时,,
,
;
②当时,,
,
,
③当时,,
,
此时点与点重合,
由题意可知点D不与点B、C重合,
此种情况不存在,
综上所述,当△ADE是等腰三角形时,或.
【点睛】本题考查了全等三角形的性质与判定,等腰三角形的性质与判定,三角形的外角性质,三角形的内角和定理,分了他了是解题的关键.
15.如图,等腰直角△ABC中,BC=AC,∠ACB=90°,现将该三角形放置在平面直角坐标系中,点B坐标为(0,2),点C坐标为(6,0).
(1)过点A作AD⊥x轴,求OD的长及点A的坐标;
(2)连接OA,若Р为坐标平面内不同于点A的点,且以O、P、C为顶点的三角形与△OAC全等,请直接写出满足条件的点P的坐标;
(3)已知OA=10,试探究在x轴上是否存在点Q,使△OAQ是以OA为腰的等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
【答案】(1)OD=8,点A的坐标(8,6);(2)(8,-6)或(-2,6)或(-2,-6);(3)(16,0)或(10,0)或(-10,0)
【分析】(1)通过证明△BOC≌△CDA,可得CD=OB=2,即可求OD的长,进而即可得到A的坐标;
(2)分三种情况:①作△OAC关于x轴的对称图形得到△OP1C;作△OAC关于直线x=3的对称图形得到△OP2C;③作△OP2C关于x轴的对称图形得到△OP3C,分别求解,即可;
(3)分三种情况:①当以点A为顶角顶点时,且OA是腰;②当以点A为底角顶点时,且OA是腰,形成锐角三角形时;③当以点A为底角顶点时,且OA是腰,形成钝角三角形时,分别求解即可.
【详解】解:(1)∵点B坐标为(0,2),点C坐标为(6,0),∴OB=2,OC=6,
∵∠ACB=90°,∴∠BCO+∠ACD=90°,且∠BCO+∠OBC=90°,
∴∠ACD=∠OBC,且AC=BC,∠BOC=∠ADC=90°,
∴△BOC≌△CDA(AAS),∴CD=OB=2,∴OD=OC+CD=8,AD=OC=6,∴点A的坐标(8,6);
(2)①作△OAC关于x轴的对称图形得到△OP1C,∴△OAC△OP1C,∴P1(8,-6);
②∵点O,C关于直线x=3对称,∴作△OAC关于直线x=3的对称图形得到△OP2C,
∴△OAC△CP2O,∴P2(-2,6);
③作△OP2C关于x轴的对称图形得到△OP3C,
∴△OP2C△OP3C,即:△OP3C△OCA,∴P3(-2,-6),
综上所述:P的坐标为:(8,-6)或(-2,6)或(-2,-6);
(3)①当以点A为顶角顶点时,且OA是腰,
∵AD⊥x轴,∴点Q1,O关于直线AD对称,即:Q1(16,0);
②当以点A为底角顶点时,且OA是腰,形成锐角三角形时,
则OQ2=OA=10,∴Q2(10,0);
③当以点A为底角顶点时,且OA是腰,形成钝角三角形时,
则OQ3=OA=10,∴Q2(-10,0),
综上所述:Q的坐标为:(16,0)或(10,0)或(-10,0).
【点睛】本题考查了全等三角形的判定和性质,坐标与图形性质,等腰三角形的性质等知识,灵活运用这些性质进行推理,掌握分类讨论思想方法是本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
全等模型专题2——一线三等角(K字)模型
全等三角形在中考数学几何模块中占据着重要地位,也是学生必须掌握的一块内容,本专题就全等三角形中的重要模型(一线三等角(K字)模型)进行梳理及对应试题分析,方便掌握。
模型1.一线三等角(K型图)模型(同侧型)
【模型解读】
在某条直线上有三个角相等,利用平角为180°与三角形内角和为180°,证得两个三角形全等。
【常见模型及证法】
同侧型一线三等角(常见):
锐角一线三等角 直角一线三等角(“K型图”) 钝角一线三等角
条件:+ CE=DE
证明思路:+任一边相等
例1.(1)如图1,已知:在中,,直线m经过点A,直线m,直线m,垂足分别为点D、E.证明:.
(2)如图2,将(1)中的条件改为:在△ABC中,,D、A、E三点都在直线m上,并且有,其中为任意钝角,请问结论是否成立?如成立,请你给出证明;若不成立,请说明理由.
例2.在直线上依次取互不重合的三个点,在直线上方有,且满足.
(1)如图1,当时,猜想线段之间的数量关系是____________;
(2)如图2,当时,问题(1)中结论是否仍然成立?如成立,请你给出证明;若不成立,请说明理由;(3)应用:如图3,在中,是钝角,,,直线与的延长线交于点,若,的面积是12,求与的面积之和.
例3.如图(1)AB=9cm,AC⊥AB,BD⊥AB,AC=BD=7cm,点P在线段AB上以2cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动,它们运动的时间为t(s).(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由;(2)在(1)的前提条件下,判断此时线段PC和线段PQ的位置关系,并证明;(3)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=50°”,其他条件不变.设点Q的运动速度为xcm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
例4.(1)探索发现:如图1,已知中,,,直线l过点C,过点A作,过点B作,垂足分别为D、E.求证:.
(2)迁移应用:如图2,将一块等腰直角的三角板放在平面直角坐标系内,三角板的一个锐角的顶点与坐标原点O重合,另两个顶点均落在第一象限内,已知点N的坐标为,求点M的坐标.
(3)拓展应用:如图3,在平面直角坐标系内,已知直线与y轴交于点P,与x轴交于点Q,将直线绕P点沿逆时针方向旋转后,所得的直线交x轴于点R.求点R的坐标.
模型2.一线三等角(K型图)模型(异侧型)
【模型解读】在某条直线上有三个角相等,利用平角为180°与三角形内角和为180°,证得两个三角形全等。
【常见模型及证法】
异侧型一线三等角:
锐角一线三等角 直角一线三等角 钝角一线三等角
条件:+ 任意一边相等
证明思路:+任一边相等
例1.老师在上课时,在黑板上写了一道题:
“如图,ABCD是正方形,点E在BC上,DF⊥AE于F,请问图中是否存在一组全等三角形?”
小杰同学经过思考发现:△ADF≌△EAB.
理由如下:因为ABCD是正方形(已知)所以∠B=90°且AD=AB和AD∥BC
又因为DF⊥AE(已知)即∠DFA=90°(垂直的意义)
所以∠DFA=∠B(等量代换)
又AD∥BC 所以∠1=∠2(两直线平行,内错角相等)
在△ADF和△EAB中所以△ADF≌△EAB(AAS)
小胖却说这题是错误的,这两个三角形根本不全等.
你知道小杰的错误原因是什么吗?我们再添加一条线段,就能找到与△ADF全等的三角形,请能说出此线段的做法吗?并说明理由.
例2.(1)课本习题回放:“如图①,,,,,垂足分别为,,,.求的长”,请直接写出此题答案:的长为________.
(2)探索证明:如图②,点,在的边、上,,点,在内部的射线上,且.求证:.
(3)拓展应用:如图③,在中,,.点在边上,,点、在线段上,.若的面积为15,则与的面积之和为________.(直接填写结果,不需要写解答过程)
例3.过正方形(四边都相等,四个角都是直角)的顶点作一条直线.
(1)当不与正方形任何一边相交时,过点作于点,过点作于点如图(1),请写出,,之间的数量关系,并证明你的结论.
(2)若改变直线的位置,使与边相交如图(2),其它条件不变,,,的关系会发生变化,请直接写出,,的数量关系,不必证明;
(3)若继续改变直线的位置,使与边相交如图(3),其它条件不变,,,的关系又会发生变化,请直接写出,,的数量关系,不必证明.
课后专项训练
1.如图,在平面直角坐标系中、,轴,存在第一象限的一点使得是以为斜边的等腰直角三角形,则点的坐标( ).
A.或 B. C.或 D.
第1题图 第2题图
2.如图,在△ABC中,AB=AC=9,点E在边AC上,AE的中垂线交BC于点D,若∠ADE=∠B,CD=3BD,则CE等于( )
A.3 B.2 C. D.
3.如图,桌面上竖直放置着一个等腰直角三角板,若测得斜边的两端点到桌面的距离分别为,.(1)求证:;(2)若,,求的长.
4.(1)【问题发现】如图1,△ABC与△CDE中,∠B=∠E=∠ACD=90°,AC=CD,B、C、E三点在同一直线上,AB=3,ED=4,则BE=_____.
(2)【问题提出】如图2,在Rt△ABC中,∠ABC=90°,BC=4,过点C作CD⊥AC,且CD=AC,求△BCD的面积.(3)【问题解决】如图3,四边形ABCD中,∠ABC=∠CAB=∠ADC=45°,△ACD面积为12且CD的长为6,求△BCD的面积.
5.在一次课题学习活动中,老师提出了如下问题:如图,四边形是正方形,点是边的中点,,且交正方形外角平分线于点.请你探究与存在怎样的数量关系,并证明你的结论正确.经过探究,小明得出的结论是,而要证明结论,就需要证明和所在的两个三角形全等,但和显然不全等(一个是直角三角形,一个是钝角三角形),考虑到点是边的中点,小明想到的方法是如图2,取的中点,连接,证明.从而得到.请你参考小明的方法解决下列问题.
(1)如图3,若把条件“点是边的中点”改为“点是边上的任意一点”,其余条件不变,证明结论仍然成立;(2)如图4,若把条件“点是边的中点”改为:“点是边延长线上的一点”,其余条件仍不变,那么结论是否还成立?若成立,请完成证明过程,若不成立,请说明理由.
6.平面内有一等腰直角三角板(∠ACB=90°)和一直线MN.过点C作CE⊥MN于点E,过点B作BF⊥MN于点F.当点E与点A重合时(如图1),易证:AF+BF=2CE.
(1)当三角板绕点A顺时针旋转至图2的位置时,上述结论是否仍然成立?若成立,请给予证明;若不成立,线段AF、BF、CE之间又有怎样的数量关系,请直接写出你的猜想,不需证明.
(2)当三角板绕点A顺时针旋转至图3的位置时,上述结论是否仍然成立?若成立,请给予证明;若不成立,线段AF、BF、CE之间又有怎样的数量关系,请直接写出你的猜想,不需证明.
7.如图1,在中,,,直线经过点,且于,于.(1)由图1,证明:;
(2)当直线绕点旋转到图2的位置时,请猜想出,,的等量关系并说明理由;
(3)当直线绕点旋转到图3的位置时,试问,,又具有怎样的等量关系?请直接写出这个等量关系(不必说明理由).
8.【初步探究】
(1)如图1,在四边形中,,E是边上一点,,连接.请判断的形状,并说明理由.
【问题解决】(2)若设,试利用图1验证勾股定理.
【拓展应用】(3)如图2,在平面直角坐标系中,已知点,点,点C在第一象限内,若为等腰直角三角形,求点C的坐标.
9.通过对下面数学模型的研究学习,解决下列问题:
【模型呈现】(1)如图,,,过点作于点,过点作于点.由,得.又,可以推理得到.进而得到___________,___________.我们把这个数学模型称为“字”模型或“一线三等角”模型;
【模型应用】(2)①如图,,,,连接,,且于点,与直线交于点.求证:点是的中点;②如图,在平面直角坐标系中,点的坐标为,点为平面内任一点.若是以为斜边的等腰直角三角形,请直接写出点的坐标.
10.通过对数学模型“K字”模型或“一线三等角”模型的研究学习,解决下列问题:
[模型呈现]如图1,,,过点B作于点C,过点D作于点E.求证:.
[模型应用]如图2,且,且,请按照图中所标注的数据,计算图中实线所围成的图形的面积为________________.
[深入探究]如图3,,,,连接,,且于点F,与直线交于点G.若,,则的面积为_____________.
11.在中,,,为直线上一点,连接,过点作交于点,交于点,在直线上截取,连接.
(1)当点,都在线段上时,如图①,求证:;
(2)当点在线段的延长线上,点在线段的延长线上时,如图②;当点在线段的延长线上,点在线段的延长线上时,如图③,直接写出线段,,之间的数量关系,不需要证明.
12.(1)如图,等腰直角中,,,线段经过点,过A作于点,过作于求证:≌.
(2)如图,已知在平面直角坐标系中,为坐标原点,点的坐标为,点的坐标为,点是平面直角坐标系中的一点,若是以为直角边的等腰直角三角形,求点的坐标;
(3)如图,已知在平面直角坐标系中,为坐标原点,在等腰直角中,,,点在线段上从向运动运动到点停止,以点为直角顶点向右上方做等腰直角,求点移动的距离.
13.已知:CD是经过∠BCA的顶点C的一条直线,CA=CB,E、F是直线CD上两点,∠BEC=∠CFA=∠α.
(1)若直线CD经过∠BCA的内部,∠BCD>∠ACD.
①如图1,∠BCA=90°,∠α=90°,写出BE,EF,AF间的等量关系: .
②如图2,∠α与∠BCA具有怎样的数量关系,能使①中的结论仍然成立?写出∠α与∠BCA的数量关系 .
(2)如图3.若直线CD经过∠BCA的外部,∠α=∠BCA,①中的结论是否成立?若成立,进行证明;若不成立,写出新结论并进行证明.
14.如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(点D不与点B、C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.
(1)当∠BDA=105°时,∠EDC= °,∠DEC= °;点D从点B向点C运动时,∠BDA逐渐变 .(填“大”或“小”)。(2)当DC等于多少时,△ABD≌△DCE?请说明理由.
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数;若不可以,请说明理由.
15.如图,等腰直角△ABC中,BC=AC,∠ACB=90°,现将该三角形放置在平面直角坐标系中,点B坐标为(0,2),点C坐标为(6,0).
(1)过点A作AD⊥x轴,求OD的长及点A的坐标;
(2)连接OA,若Р为坐标平面内不同于点A的点,且以O、P、C为顶点的三角形与△OAC全等,请直接写出满足条件的点P的坐标;
(3)已知OA=10,试探究在x轴上是否存在点Q,使△OAQ是以OA为腰的等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
八年级全等模型专题2——一线三等角(K字)模型
全等三角形在中考数学几何模块中占据着重要地位,也是学生必须掌握的一块内容,本专题就全等三角形中的重要模型(一线三等角(K字)模型)进行梳理及对应试题分析,方便掌握。
模型1.一线三等角(K型图)模型(同侧型)
【模型解读】
在某条直线上有三个角相等,利用平角为180°与三角形内角和为180°,证得两个三角形全等。
【常见模型及证法】
同侧型一线三等角(常见):
锐角一线三等角 直角一线三等角(“K型图”) 钝角一线三等角
条件:+ CE=DE
证明思路:+任一边相等
例1.(2023·浙江·八年级假期作业)(1)如图1,已知:在中,,直线m经过点A,直线m,直线m,垂足分别为点D、E.证明:.
(2)如图2,将(1)中的条件改为:在△ABC中,,D、A、E三点都在直线m上,并且有,其中为任意钝角,请问结论是否成立?如成立,请你给出证明;若不成立,请说明理由.
【答案】(1)见解析;(2)成立,见解析
【分析】(1)根据可证明,可得,可得.
(2)由已知条件可知,,可得,结合条件可证明,同(1)可得出结论.
【详解】证明:(1)如图1,
∵直线m,直线m,∴,
∵,∴,
∵,∴,
在和中,∴,
∴,∴;
(2)如图2,
∵,∴,∴,
在和中,∴,
∴,∴.
【点睛】本题主要考查了全等三角形的判定和性质,由条件证明三角形全等得到是解题的关键.
例2.(2023春·上海·七年级专题练习)在直线上依次取互不重合的三个点,在直线上方有,且满足.
(1)如图1,当时,猜想线段之间的数量关系是____________;
(2)如图2,当时,问题(1)中结论是否仍然成立?如成立,请你给出证明;若不成立,请说明理由;(3)应用:如图3,在中,是钝角,,,直线与的延长线交于点,若,的面积是12,求与的面积之和.
【答案】(1)DE=BD+CE(2)DE=BD+CE仍然成立,理由见解析(3)△FBD与△ACE的面积之和为4
【分析】(1)由∠BDA=∠BAC=∠AEC=90°得到∠BAD+∠EAC=∠BAD+∠DBA=90°,进而得到∠DBA=∠EAC,然后结合AB=AC得证△DBA≌△EAC,最后得到DE=BD+CE;
(2)由∠BDA=∠BAC=∠AEC=α得到∠BAD+∠EAC=∠BAD+∠DBA=180°﹣α,进而得到∠DBA=∠EAC,然后结合AB=AC得证△DBA≌△EAC,最后得到DE=BD+CE;
(3)由∠BAD>∠CAE,∠BDA=∠AEC=∠BAC,得出∠CAE=∠ABD,由AAS证得△ADB≌△CAE,得出S△ABD=S△CEA,再由不同底等高的两个三角形的面积之比等于底的比,得出S△ABF即可得出结果.
【详解】(1)解:DE=BD+CE,理由如下,∵∠BDA=∠BAC=∠AEC=90°,
∴∠BAD+∠EAC=∠BAD+∠DBA=90°,∴∠DBA=∠EAC,
∵AB=AC,∴△DBA≌△EAC(AAS),∴AD=CE,BD=AE,
∴DE=AD+AE=BD+CE,故答案为:DE=BD+CE.
(2)DE=BD+CE仍然成立,理由如下,∵∠BDA=∠BAC=∠AEC=α,
∴∠BAD+∠EAC=∠BAD+∠DBA=180°﹣α,∴∠DBA=∠EAC,
∵AB=AC,∴△DBA≌△EAC(AAS),
∴BD=AE,AD=CE,∴DE=AD+AE=BD+CE;
(3)解:∵∠BAD<∠CAE,∠BDA=∠AEC=∠BAC,∴∠CAE=∠ABD,
在△ABD和△CAE中,,∴△ABD≌△CAE(AAS),∴S△ABD=S△CAE,
设△ABC的底边BC上的高为h,则△ABF的底边BF上的高为h,
∴S△ABC=BC h=12,S△ABF=BF h,∵BC=3BF,∴S△ABF=4,
∵S△ABF=S△BDF+S△ABD=S△FBD+S△ACE=4,∴△FBD与△ACE的面积之和为4.
【点睛】本题考查了全等三角形的判定与性质、直角三角形的性质,三角形的面积,解题的关键是熟练掌握全等三角形的判定与性质.
例3.(2022春·广东梅州·七年级校考阶段练习)如图(1)AB=9cm,AC⊥AB,BD⊥AB,AC=BD=7cm,点P在线段AB上以2cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动,它们运动的时间为t(s).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由;
(2)在(1)的前提条件下,判断此时线段PC和线段PQ的位置关系,并证明;
(3)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=50°”,其他条件不变.设点Q的运动速度为xcm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
【答案】(1)△ACP与△BPQ全等,理由见解析;(2)PC⊥PQ,证明见解析;(3)存在,当t=1s,x=2cm/s或t=s,x=cm/s时,△ACP与△BPQ全等.
【分析】(1)利用定理证明;(2)根据全等三角形的性质判断线段和线段的位置关系;(3)分,两种情况,根据全等三角形的性质列式计算.
【详解】(1)△ACP与△BPQ全等,
理由如下:当t=1时,AP=BQ=2,则BP=9﹣2=7,∴BP=AC,又∵∠A=∠B=90°,
在△ACP和△BPQ中,,∴△ACP≌△BPQ(SAS);
(2)PC⊥PQ,证明:∵△ACP≌△BPQ,∴∠ACP=∠BPQ,
∴∠APC+∠BPQ=∠APC+∠ACP=90°.∴∠CPQ=90°,即线段PC与线段PQ垂直;
(3)①若△ACP≌△BPQ,则AC=BP,AP=BQ,
∴9﹣2t=7,解得,t=1(s),则x=2(cm/s);
②若△ACP≌△BQP,则AC=BQ,AP=BP,则2t=×9,
解得,t=(s),则x=7÷=(cm/s),
故当t=1s,x=2cm/s或t=s,x=cm/s时,△ACP与△BPQ全等.
【点睛】本题考查的是全等三角形的判定与性质,掌握全等三角形的判定定理和性质定理、注意分
类讨论思想的灵活运用是解题的关键.
例4.(2022·贵州铜仁·三模)(1)探索发现:如图1,已知中,,,直线l过点C,过点A作,过点B作,垂足分别为D、E.求证:.
(2)迁移应用:如图2,将一块等腰直角的三角板放在平面直角坐标系内,三角板的一个锐角的顶点与坐标原点O重合,另两个顶点均落在第一象限内,已知点N的坐标为,求点M的坐标.
(3)拓展应用:如图3,在平面直角坐标系内,已知直线与y轴交于点P,与x轴交于点Q,将直线绕P点沿逆时针方向旋转后,所得的直线交x轴于点R.求点R的坐标.
【答案】(1)见详解;(2)点M的坐标为(1,3);(3)R(,0)
【分析】(1)先判断出∠ACB=∠ADC,再判断出∠CAD=∠BCE,进而判断出△ACD≌△CBE,即可得出结论;(2)过点M作MF⊥y轴,垂足为F,过点N作NG⊥MF,判断出MF=NG,OF=MG,设M(m,n)列方程组求解,即可得出结论;(3)过点Q作QS⊥PQ,交PR于S,过点S作SH⊥x轴于H,先求出OP=4,由y=0得x=1,进而得出Q(1,0),OQ=1,再判断出PQ=SQ,即可判断出OH=5,SH=OQ=1,进而求出直线PR的解析式,即可得出结论.
【详解】(1)证明:∵∠ACB=90°,AD⊥l,∴∠ACB=∠ADC.
∵∠ACE=∠ADC+∠CAD,∠ACE=∠ACB+∠BCE,∴∠CAD=∠BCE,
∵∠ADC=∠CEB=90°,AC=BC.∴△ACD≌△CBE,∴CD=BE,
(2)解:如图2,过点M作MF⊥y轴,垂足为F,过点N作NG⊥MF,交FM的延长线于G,
由已知得OM=ON,且∠OMN=90°,∴由(1)得△OFM≌△MGN,
∴MF=NG,OF=MG,设M(m,n),∴MF=m,OF=n,∴MG=n,NG=m,
∵点N的坐标为(4,2)∴解得∴点M的坐标为(1,3);
(3)如图3,过点Q作QS⊥PQ,交PR于S,过点S作SH⊥x轴于H,
对于直线y=﹣4x+4,由x=0得y=4,
∴P(0,4),∴OP=4,由y=0得x=1,∴Q(1,0),OQ=1,
∵∠QPR=45°,∴∠PSQ=45°=∠QPS.∴PQ=SQ.∴由(1)得SH=OQ,QH=OP.
∴OH=OQ+QH=OQ+OP=4+1=5,SH=OQ=1.∴S(5,1),
设直线PR为y=kx+b,则,解得.∴直线PR为y=x+4.
由y=0得,x=,∴R(,0).
【点睛】本题是一次函数综合题,主要考查了待定系数法,全等三角形的判定和性质,构造出全等三角形是解本题的关键.
模型2.一线三等角(K型图)模型(异侧型)
【模型解读】在某条直线上有三个角相等,利用平角为180°与三角形内角和为180°,证得两个三角形全等。
【常见模型及证法】
异侧型一线三等角:
锐角一线三等角 直角一线三等角 钝角一线三等角
条件:+ 任意一边相等
证明思路:+任一边相等
例1.(2022·浙江杭州·一模)老师在上课时,在黑板上写了一道题:
“如图,ABCD是正方形,点E在BC上,DF⊥AE于F,请问图中是否存在一组全等三角形?”
小杰同学经过思考发现:△ADF≌△EAB.
理由如下:因为ABCD是正方形(已知)所以∠B=90°且AD=AB和AD∥BC
又因为DF⊥AE(已知)即∠DFA=90°(垂直的意义)
所以∠DFA=∠B(等量代换)
又AD∥BC 所以∠1=∠2(两直线平行,内错角相等)
在△ADF和△EAB中所以△ADF≌△EAB(AAS)
小胖却说这题是错误的,这两个三角形根本不全等.
你知道小杰的错误原因是什么吗?我们再添加一条线段,就能找到与△ADF全等的三角形,请能说出此线段的做法吗?并说明理由.
【答案】小杰错误的原因是AD和AB不是对应边,在证明两个三角形全等时,误以为对应边了;线段为作BH⊥AE于点H,证明见详解;
【分析】根据小杰的证明方法,可以发现,在证明两个三角形全等时,出现了问题,然后说出出错的原因即可,然后添加合适的辅助线段,说明与△ADF全等的三角形成立的理由即可解答本题;
【详解】小杰错误的原因是AD和AB不是对应边,在证明两个三角形全等时,误以为对应边了,作BH⊥AE于H,则△ADF≌△BAH;
∵四边形ABCD是正方形,∴AD=BA,∠DAB=90°,∴∠HAB+∠FAD=90°,
∵DF⊥AE,BH⊥AE,∴∠DFA=∠AHB=90°,
∴∠HAB+∠HBA=90°,∴∠FAD=∠HBA,
在△ADF和△BAH中 ∴△ADF≌△BAH(AAS);
【点睛】本题考查正方形的性质、全等三角形的判定,解答本题的关键是明确题意,利用数形结合的思想解答;
例2.(2022·山东·九年级课时练习)(1)课本习题回放:“如图①,,,,,垂足分别为,,,.求的长”,请直接写出此题答案:的长为________.
(2)探索证明:如图②,点,在的边、上,,点,在内部的射线上,且.求证:.
(3)拓展应用:如图③,在中,,.点在边上,,点、在线段上,.若的面积为15,则与的面积之和为________.(直接填写结果,不需要写解答过程)
【答案】(1)0.8cm;(2)见解析(3)5
【分析】(1)利用AAS定理证明△CEB≌△ADC,根据全等三角形的性质解答即可;
(2)由条件可得∠BEA=∠AFC,∠4=∠ABE,根据AAS可证明△ABE≌△CAF;
(3)先证明△ABE≌△CAF,得到与的面积之和为△ABD的面积,再根据故可求解.
【详解】解:(1)∵BE⊥CE,AD⊥CE,∴∠E=∠ADC=90°,∴∠EBC+∠BCE=90°.
∵∠BCE+∠ACD=90°,∴∠EBC=∠DCA.在△CEB和△ADC中,
∴△CEB≌△ADC(AAS),∴BE=DC,CE=AD=2.5cm.
∵DC=CE DE,DE=1.7cm,∴DC=2.5 1.7=0.8cm,∴BE=0.8cm故答案为:0.8cm;
(2)证明:∵∠1=∠2,∴∠BEA=∠AFC.
∵∠1=∠ABE+∠3,∠3+∠4=∠BAC,∠1=∠BAC,
∴∠BAC=∠ABE+∠3,∴∠4=∠ABE.
∵∠AEB=∠AFC,∠ABE=∠4,AB=AC,∴△ABE≌△CAF(AAS).
(3)∵∴∠ABE+∠BAE=∠FAC+∠BAE=∠FAC+∠ACF
∴∠ABE=∠CAF,∠BAE=∠ACF 又∴△ABE≌△CAF,∴
∴与的面积之和等于与的面积之和,即为△ABD的面积,
∵,△ABD与△ACD的高相同则=5
故与的面积之和为5故答案为:5.
【点睛】本题考查的是全等三角形的判定和性质、三角形内角和定理,掌握全等三角形的判定定理和性质定理是解题的关键.
例3.(2023·贵州遵义·八年级统考期末)过正方形(四边都相等,四个角都是直角)的顶点作一条直线.
(1)当不与正方形任何一边相交时,过点作于点,过点作于点如图(1),请写出,,之间的数量关系,并证明你的结论.
(2)若改变直线的位置,使与边相交如图(2),其它条件不变,,,的关系会发生变化,请直接写出,,的数量关系,不必证明;
(3)若继续改变直线的位置,使与边相交如图(3),其它条件不变,,,的关系又会发生变化,请直接写出,,的数量关系,不必证明.
【答案】(1),证明见解析;(2);(3)
【分析】(1)根据同角的余角相等可证,再证,根据全等三角形的对应边相等进行代换即可;(2)根据同角的余角相等可证,再证,根据全等三角形的对应边相等进行代换即可;(3)根据同角的余角相等可证,再证,根据全等三角形的对应边相等进行代换即可.
【详解】(1),证明:
四边形是正方形,
又, ∴
在和中
,
(2),理由是:四边形是正方形 ,
又, ∴
在和中
, ∴EF=AF-AE=BE-DF
(3),理由是:
四边形是正方形,
又, ∴
在和中
, EF=AE-AF=DF-BE
【点睛】本题考查的是三角形全等的判定和性质,掌握三角形的判定方法及能利用同角的余角相等证明是关键.
课后专项训练
1.(2022·贵州·凯里一模)如图,在平面直角坐标系中、,轴,存在第一象限的一点使得是以为斜边的等腰直角三角形,则点的坐标( ).
A.或 B. C.或 D.
【答案】C
【分析】分点P在AB的上方和点P在AB的下方,根据全等三角形的判定与性质进行讨论求解即可.
【详解】解:当点P在AB的上方时,过P作x轴的平行线交y轴于E,交CB延长线于F,如图1,
则∠AEP=∠PFB=∠APB=90°,E(0,2a﹣5),F(6,2a﹣5),∴PE=a,PF=6﹣a,AE=2a﹣9,
∵∠EAP+∠EPA=90°,∠EPA+∠BPF=90°,∴∠EAP=∠BPF,又∠AEP=∠PFB,PA=PB,
∴△AEP≌△PFB(AAS),∴AE=PF,∴6﹣a=2a﹣9,解得:a=5,∴P(5,5);
当点P在AB的下方时,同样过P作x轴的平行线交y轴于E,交CB于F,如图2,
则∠AEP=∠PFB=∠APB=90°,E(0,2a﹣5),F(6,2a﹣5),∴PE=a,PF=6﹣a,AE=9﹣2a,
∵∠EAP+∠EPA=90°,∠EPA+∠BPF=90°,∴∠EAP=∠BPF,又∠AEP=∠PFB,PA=PB,
∴△AEP≌△PFB(AAS),∴AE=PF,∴9﹣2a=6﹣a,解得:a=3,∴P(3,1),
综上,点P的坐标为(3,1)或(5,5),故选:C.
【点睛】本题考查等腰直角三角形的性质、全等三角形的判定与性质、等角的余角相等、坐标与图形性质、解一元一次方程等知识,过已知点向坐标轴作平行线或垂线,然后求出相关线段的长是解决此类问题的基本方法.
2.(2023·浙江·八年级假期作业)如图,在△ABC中,AB=AC=9,点E在边AC上,AE的中垂线交BC于点D,若∠ADE=∠B,CD=3BD,则CE等于( )
A.3 B.2 C. D.
【答案】A
【分析】根据等腰三角形的性质得到∠B=∠C,推出∠BAD=∠CDE,根据线段垂直平分线的性质得到AD=ED,根据全等三角形的性质得到CD=AB=9,BD=CE,即可得到结论.
【详解】解:∵AB=AC=9,∴∠B=∠C,
∵∠ADE=∠B,∠BAD=180°﹣∠B﹣∠ADB,∠CDE=180°﹣∠ADE﹣∠ADB,
∴∠BAD=∠CDE,∵AE的中垂线交BC于点D,∴AD=ED,
在△ABD与△DCE中,,
∴△ABD≌△DCE(AAS),∴CD=AB=9,BD=CE,
∵CD=3BD,∴CE=BD=3故选:A.
【点睛】本题考查了等腰三角形的性质,线段垂直平分线的性质,全等三角形的性质,属于基础题.
3.(2022·河北保定·模拟预测)如图,桌面上竖直放置着一个等腰直角三角板,若测得斜边的两端点到桌面的距离分别为,.(1)求证:;(2)若,,求的长.
【答案】(1)见解析;(2)3
【分析】(1)先利用同角的余角相等,判断出∠DAC=∠BCE,进而判断出△ACD≌△CBE;
(2)由全等三角形的性质,即可求出答案.
【详解】解:(1)证明:∵,,
∴,∴.
∵,∴,∴,
∴.∴
(2)解:∵,∴,.∵,∴,
∵,∴,∴.
【点睛】此题主要考查了等腰直角三角形的性质,全等三角形的判定和性质,判断出△ACD≌△CBE是解本题的关键.
4.(1)【问题发现】如图1,△ABC与△CDE中,∠B=∠E=∠ACD=90°,AC=CD,B、C、E三点在同一直线上,AB=3,ED=4,则BE=_____.
(2)【问题提出】如图2,在Rt△ABC中,∠ABC=90°,BC=4,过点C作CD⊥AC,且CD=AC,求△BCD的面积.(3)【问题解决】如图3,四边形ABCD中,∠ABC=∠CAB=∠ADC=45°,△ACD面积为12且CD的长为6,求△BCD的面积.
【答案】(1)7;(2)S△BCD=8;(3)S△BCD=6.
【分析】(1) ∠B=∠E=∠ACD=90°,根据同角的余角相等,可得∠ACB=∠D,由已知条件可证△ABC≌△CED,可得答案;
(2)过D作DE⊥BC交BC延长线于E,同(1)中的方法,可证△ABC≌△CED,可得答案;
(3)过A作AE⊥CD于E,过B作BF⊥CD交DC延长线于F,由△ACD面积为12且CD的长为6,可得AE=4,进而可得CE=2,同(1)中证法,可得△ACE≌△CBF,由全等三角形的性质可求得答案.
【详解】解:(1)∵∠ACD=∠E=90°,∴∠ACB=90°﹣∠DCE=∠D,
在△ABC和△CED中,,∴△ABC≌△CED(AAS),
∴AB=CE=3,BC=ED=4,∴BE=BC+CE=7;故答案为:7;
(2)过D作DE⊥BC交BC延长线于E,如图:
∵DE⊥BC,CD⊥AC,∴∠E=∠ACD=90°,∴∠ACB=90°﹣∠DCE=∠CDE,
在△ABC和△CED中,,∴△ABC≌△CED(AAS),
∴BC=ED=4,∴S△BCD=BC DE=8;
(3)过A作AE⊥CD于E,过B作BF⊥CD交DC延长线于F,如图:
∵△ACD面积为12且CD的长为6,∴×6 AE=12,∴AE=4,
∵∠ADC=45°,AE⊥CD,∴△ADE是等腰直角三角形,∴DE=AE=4,∴CE=CD﹣DE=2,
∵∠ABC=∠CAB=45°,∴∠ACB=90°,AC=BC,∴∠ACE=90°﹣∠BCF=∠CBF,
在△ACE和△CBF中,,∴△ACE≌△CBF(AAS),
∴BF=CE=2,∴S△BCD=CD BF=6.
【点睛】本题考查全等三角形的性质与判定,属于类比探究类的题目,掌握模型思想,准确作出辅助线构造全等三角形是解题的关键.
5.在一次课题学习活动中,老师提出了如下问题:如图,四边形是正方形,点是边的中点,,且交正方形外角平分线于点.请你探究与存在怎样的数量关系,并证明你的结论正确.经过探究,小明得出的结论是,而要证明结论,就需要证明和所在的两个三角形全等,但和显然不全等(一个是直角三角形,一个是钝角三角形),考虑到点是边的中点,小明想到的方法是如图2,取的中点,连接,证明.从而得到.请你参考小明的方法解决下列问题.
(1)如图3,若把条件“点是边的中点”改为“点是边上的任意一点”,其余条件不变,证明结论仍然成立;(2)如图4,若把条件“点是边的中点”改为:“点是边延长线上的一点”,其余条件仍不变,那么结论是否还成立?若成立,请完成证明过程,若不成立,请说明理由.
【答案】(1)正确,见解析;(2)正确,见解析
【分析】(1)在AB上取点,连接,证明△PAE≌△CEF即可;
(2)延长BA至,使=CE,连接,证明△ANE≌△ECF即可.
【详解】解:(1)正确.证明:在AB上取一点M,使AM=EC,连接ME.
四边形是正方形,
∴BM=BE,∴∠BME=45°,∴∠AME=135°,
∵CF是外角平分线,∴∠DCF=45°,∴∠ECF=135°,∴∠AME=∠ECF,
∵∠AEB+∠BAE=90°,∠AEB+∠CEF=90°,∴∠BAE=∠CEF,
∴△AME≌△ECF(ASA),∴AE=EF.
(2)正确.证明:在BA的延长线上取一点N.
使AN=CE,连接NE.∴BN=BE,∴∠N=∠NEC=45°,
∵CF平分∠DCG,∴∠FCE=45°,∴∠N=∠ECF,
∵四边形ABCD是正方形,∴AD∥BE,∴∠DAE=∠BEA,
即∠DAE+90°=∠BEA+90°,∴∠NAE=∠CEF,∴△ANE≌△ECF(ASA)∴AE=EF.
【点睛】本题考查的是构造三角形全等证明线段的相等,同时考查了正方形的性质,掌握构造全等三角形是解题关键.
6.平面内有一等腰直角三角板(∠ACB=90°)和一直线MN.过点C作CE⊥MN于点E,过点B作BF⊥MN于点F.当点E与点A重合时(如图1),易证:AF+BF=2CE.
(1)当三角板绕点A顺时针旋转至图2的位置时,上述结论是否仍然成立?若成立,请给予证明;若不成立,线段AF、BF、CE之间又有怎样的数量关系,请直接写出你的猜想,不需证明.
(2)当三角板绕点A顺时针旋转至图3的位置时,上述结论是否仍然成立?若成立,请给予证明;若不成立,线段AF、BF、CE之间又有怎样的数量关系,请直接写出你的猜想,不需证明.
【答案】(1)AF+BF=2CE仍成立 (2)AF-BF=2CE
【分析】(1)过B作BH⊥CE于点H,可证△ACE≌△CBH,通过线段的等量代换可得结论;
(2)过点B作BG⊥CE,交CE的延长线于点G,△ACE≌△CBG,通过线段的等量代换可得答案.
(1)解:图2,AF+BF=2CE仍成立,
证明:如图,过B作BH⊥CE于点H,
∵∠BCH+∠ACE=90°,又∵在直角△ACE中,∠ACE+∠CAE=90°,∴∠CAE=∠BCH,
又∵AC=BC,∠AEC=∠BHC=90°∴△ACE≌△CBH.∴CH=AE,BF=HE,CE=BH,
∴AF+BF=AE+EF+BF=CH+EF+HE=CE+EF=2EC.
(2)解:不成立,线段AF、BF、CE之间的数量关系为:AF-BF=2CE
证明:如图,过点B作BG⊥CE,交CE的延长线于点G,
∵∠BCG+∠ACE=90°,又∵在直角△ACE中,∠ACE+∠CAE=90°,∴∠CAE=∠BCG,
又∵AC=BC,∠AEC=∠BGC=90°∴△ACE≌△CBG.∴CG=AE,BF=GE,CE=BG,
∴AF-BF=AE+EF-BF=CG+EF-GE=CE+EF=2EC.
【点睛】本题考查全等三角形的判定,根据题意正确作出辅助线构造全等三角形是解题的关键.
7.如图1,在中,,,直线经过点,且于,于.(1)由图1,证明:;
(2)当直线绕点旋转到图2的位置时,请猜想出,,的等量关系并说明理由;
(3)当直线绕点旋转到图3的位置时,试问,,又具有怎样的等量关系?请直接写出这个等量关系(不必说明理由).
【答案】(1)证明见解析;(2),证明过程见解析;(3),证明过程见解析
【分析】(1)先证明△ADC≌△CEB,得到AD=CE,DC=BE,进而得到DE=CE+DC=AD+BE即可;
(2)同(1)中思路,证明△ADC≌△CEB,进而得到DE=CE-DC=AD-BE即可;
(3)同(1)中思路,证明△ADC≌△CEB,进而得到DE=DC-CE=BE-AD即可.
【详解】解:(1)证明:在中,∵,∴,
∵,∴,∴,
又∵,,∴,∴,,
∵直线经过点,∴;
(2),,的等量关系为:,理由如下:
∵于,于∴,
∴,,∴,
在和中,∴
∴,,∴;
(3)当旋转到图3的位置时,、、所满足的等量关系是,理由如下:
∵于,于∴,
∴,,∴,
在和中,∴
∴,,∴.
【点睛】本题考查了全等三角形的判定方法、等腰直角三角形的性质及等角的余角相等等知识点,熟练掌握三角形全等的判定方法是求解的关键.
8.(2023春·浙江·八年级期中)【初步探究】
(1)如图1,在四边形中,,E是边上一点,,连接.请判断的形状,并说明理由.
【问题解决】(2)若设,试利用图1验证勾股定理.
【拓展应用】(3)如图2,在平面直角坐标系中,已知点,点,点C在第一象限内,若为等腰直角三角形,求点C的坐标.
【答案】(1)是等腰直角三角形,理由见解析;(2)见解析;(3)点C的坐标为(1,2)或(3,3)或.
【分析】(1)利用全等三角形的判定证明≌,再由全等三角形的性质及直角三角形的性质即可得到结论;(2)利用图形的面积建立等式进行化简即可;
(3)分三种情况,作辅助线构造全等三角形求解即可.
【详解】解:(1)是等腰直角三角形,理由如下:
在和中,,∴≌,∴AE= DE,∠AEB=∠EDC,
∵在中,∠C=90°,∴∠EDC+∠DEC= 90°,∴∠AEB+∠DEC= 90°,
∵∠AEB+∠DEC+∠AED=180°,∴∠AED=90°,∴是等腰直角三角形;
(2)由题可知,四边形ABCD为梯形,
∵≌,,,,∴AB=CE=b,BE=CD=a,
∴,
又∵,
∴,∴,∴;
(3)①当∠CAB=90°,CA=AB时,如图,过点C作CF⊥x轴于点F,过点B作BE⊥x轴于点E,
∵点A(2,0),点B(4,1),∴BE=1,OA=2,OE=4,∴AE= 2,
∵∠CAB=90°,BE⊥x轴,∴∠CAF+∠BAE= 90°,∠BAE+∠ABE=90°,∴∠CAF=∠ABE,
又∵AC= AB,∠AFC=∠AEB=90°,∴≌,
∴CF=AE= 2,AF=BE=1,∴OF=OA-AF=1,∴点C坐标为(1,2);
②当∠ABC=90°,AB=BC时,如图,过点B作BE⊥x轴于点E,过点C作CF⊥BE交EB延长线于点F,
∵∠ABC=90°,BE⊥x轴,∴∠ABE+∠CBF= 90°,∠ABE+∠BAE=90°,∴∠BAE=∠CBF,
又∵BC= AB,∠AEB=∠CFB=90°,∴≌,
∴BE=CF=1,AE=BF= 2,∴EF=3,∴点C坐标为(3,3);
③当∠ACB=90°,CA=BC时,如图,过点C作CD⊥x轴于点D,过点B作BF⊥CD于点F,BE⊥x轴于点E,
∵∠ACB=90°,CD⊥x轴,∴∠ACD+∠BCF=90°,∠ACD+∠CAD=90°,∴∠BCF=∠CAD,
又∵AC= BC,∠CDA=∠BFC=90°,∴≌,∴CF=AD, BF=CD=DE,
∵AD+DE=AE=2,∴2=AD+CD=AD+CF+DF=2AD+1,∴,
∴,,∴点C坐标为,
综上所述,点C的坐标为(1,2)或(3,3)或.
【点睛】本题考查了全等三角形的判定与性质,勾股定理的验证,平面直角坐标系中等腰直角三角形的存在性问题,熟练掌握各性质及判定定理,正确作辅助线构造出全等三角形是解题的关键.
9.通过对下面数学模型的研究学习,解决下列问题:
【模型呈现】(1)如图,,,过点作于点,过点作于点.由,得.又,可以推理得到.进而得到___________,___________.我们把这个数学模型称为“字”模型或“一线三等角”模型;
【模型应用】(2)①如图,,,,连接,,且于点,与直线交于点.求证:点是的中点;②如图,在平面直角坐标系中,点的坐标为,点为平面内任一点.若是以为斜边的等腰直角三角形,请直接写出点的坐标.
【答案】(1);(2)①证明见解析;②或
【分析】(1)根据全等三角形的对应边相等解答;(2)①作于,于,证明,,根据全等三角形的性质得到,再证明,根据全等三角形的性质证明结论;②过点作轴于点,过点作轴于点,两直线交于点,过点作轴于点,交于点,利用(1)的结论即可解答.
【详解】(1)解:∵,∴,
在和中,,∴,
∴,.故答案为:;.
(2)①证明:如图,作于,于,
∵,,∴,∴,
在和中,,∴,∴,
∵,,∴,∴,
在和中,,∴,∴,∴,
∵,,∴,
在和中,∴,∴,∴点是的中点;
②解:如图,和是以为斜边的等腰直角三角形,
∴,,
过点作轴于点,过点作轴于点,两直线交于点,过点作轴于点,交于点,∴,
∵,∴四边形是矩形,∴,,,
∵是以为斜边的等腰直角三角形,∴,,
由(1)可知,,∴,,
∵点的坐标为,∴,,
又∵,∴,
解得:,,∴点的坐标为,
∵,,,由(1)可知,,
∴,,∴点的坐标为.
综上所述,是以为斜边的等腰直角三角形,点B的坐标为或.
【点睛】本题属于三角形综合题,考查全等三角形的判定和性质、坐标与图形性质.掌握全等三角形的判定定理和性质定理是解题的关键.
10.通过对数学模型“K字”模型或“一线三等角”模型的研究学习,解决下列问题:
[模型呈现]如图1,,,过点B作于点C,过点D作于点E.求证:.
[模型应用]如图2,且,且,请按照图中所标注的数据,计算图中实线所围成的图形的面积为________________.
[深入探究]如图3,,,,连接,,且于点F,与直线交于点G.若,,则的面积为_____________.
【答案】[模型呈现]见解析;[模型应用]50;[深入探究]63
【分析】[模型呈现]证明,根据全等三角形的对应边相等得到;
[模型应用]根据全等三角形的性质得到,,,根据梯形的面积公式计算,得到答案;
[深入探究]过点D作于P,过点E作交的延长线于Q,根据全等三角形的性质得到,证明,得到,进而求出,根据三角形的面积公式计算即可.
【详解】[模型呈现]证明:∵,∴,
∵,∴,
∴,∴,
在和中,,∴,∴;
[模型应用]解:由[模型呈现]可知,,
∴,
则,
故答案为:50;
[深入探究]过点D作于P,过点E作交AG的延长线于Q,
由[模型呈现]可知,,
∴,
在和中,,∴,∴,
∵,∴,∴,
∴,∴,故答案为:63.
【点睛】本题考查的是全等三角形的判定和性质、三角形的面积计算,熟记三角形确定的判定定理是解题的关键.
11.在中,,,为直线上一点,连接,过点作交于点,交于点,在直线上截取,连接.
(1)当点,都在线段上时,如图①,求证:;
(2)当点在线段的延长线上,点在线段的延长线上时,如图②;当点在线段的延长线上,点在线段的延长线上时,如图③,直接写出线段,,之间的数量关系,不需要证明.
【答案】(1)见解析;(2)图②:;图③:
【分析】(1)过点作交的延长线于点.证明,根据全等三角形的性质可得,.再证,由此即可证得结论;(2)图②:,类比(1)中的方法证明即可;图③:,类比(1)中的方法证明即可.
【详解】(1)证明:如图,过点作交的延长线于点.
∴.∵,∴,.
∵,∴.∴.
在和中,∴.∴,.
∵,,∴.
∴.∴.
∵,,∴.
在和中,∴.∴.
∵,∴.
(2)图②:.证明:过点作交于点.
∴.∵,∴,.
∵,∴.∴.
在和中,∴.∴,.
∵,,∴.∴,
∵∴.∴.
∵,,∴.
在和中,∴.∴.
∵,∴.
图③:.
证明:如图,过点作交的延长线于点.
∴.∵,∴,.
∵,∴.∴.
在和中,∴.∴,.
∵,,∴.∴.∴.
∵,,∴.
在和中,∴.∴.
∵,∴.
【点睛】本题是全等三角形的综合题,正确作出辅助线,构造全等三角形是解决问题的关键.
12.(1)如图,等腰直角中,,,线段经过点,过A作于点,过作于求证:≌.
(2)如图,已知在平面直角坐标系中,为坐标原点,点的坐标为,点的坐标为,点是平面直角坐标系中的一点,若是以为直角边的等腰直角三角形,求点的坐标;
(3)如图,已知在平面直角坐标系中,为坐标原点,在等腰直角中,,,点在线段上从向运动运动到点停止,以点为直角顶点向右上方做等腰直角,求点移动的距离.
【答案】(1)见解析;(2),,,;(3)8
【分析】(1)根据等腰直角三角形的性质证明即可;(2)分四种情况,由(1)的结论并结合等腰直角三角形的性质即可证明;(3)过点作轴于点,过点作于点,由(1)的结论和等腰直角三角形的性质即可证明.
【详解】解:(1)为等腰直角三角形,,
又,,,,
又,,即,≌;
(2)分四种情况讨论:当点为直角顶点时,且点在左侧时,如图,过点作轴于点.
为等腰直角三角形,由(1)可知:≌,
,,,,
,,,;
其余三种情况如图所示,
同理可求得:,,;
(3)过点作轴于点,过点作于点,如图,
为等腰直角三角形,由(1)可知:≌,
,,,
点在直线上运动,当点在点时,点的坐标是,
当点在点时,点的坐标是,点运动的距离是.
【点睛】本题考查了等腰直角三角形的性质和全等三角形的判定和性质,解决本题的关键是掌握等腰直角三角形的性质.
13.已知:CD是经过∠BCA的顶点C的一条直线,CA=CB,E、F是直线CD上两点,∠BEC=∠CFA=∠α.
(1)若直线CD经过∠BCA的内部,∠BCD>∠ACD.
①如图1,∠BCA=90°,∠α=90°,写出BE,EF,AF间的等量关系: .
②如图2,∠α与∠BCA具有怎样的数量关系,能使①中的结论仍然成立?写出∠α与∠BCA的数量关系 .
(2)如图3.若直线CD经过∠BCA的外部,∠α=∠BCA,①中的结论是否成立?若成立,进行证明;若不成立,写出新结论并进行证明.
【答案】(1)①EF= BE-AF;②∠α+ ∠BCA = 180°,理由见解析;(2)不成立,EF=BE+AF,证明见解析
【分析】(1)①求出∠BEC=∠AFC = 90°, ∠CBE=∠ACF,根据AAS证△BCE≌△CAF,推出BE=CF,CE = AF即可得出结论;②求出∠BEC =∠AFC,∠CBE=∠ACF,根据AAS证△BCE≌△CAF,推出BE= CF,CE = AF即可得出结论;
(2)求出∠BEC =∠AFC,∠CBE= ∠ACF,根据AAS证△BCE≌△CAF,推出BE= CF,CE=AF即可得出结论.
【详解】(1)①EF、BE、AF的数量关系:EF= BE-AF,
证明:当α =90°时,∠BEC = ∠CFA =90°,
∵∠BCA = 90°,
∴∠BCE+∠ACF= 90°,
∵∠BCE+∠CBE =90°,
∴∠ACF = ∠CBE,
∵AC = BC,
∴△BCE≌△CAF,
∴BE =CF,CE = AF,
∵CF =CE+EF,
∴EF= CF -CE=BE-AF;
②∠α与∠BCA关系:∠α+ ∠BCA = 180°
当∠α+ ∠BCA = 180°时,①中结论仍然成立;
理由是:如题图2,
∵∠BEC = ∠CFA = ∠α, ,∠α+∠ACB =180°,
又∵
∴∠CBE= ∠ACF,
在△BCE和△CAF中
∴△BCE≌△CAF (AAS),
∴BE =CF,CE = AF,
∴EF= CF-CE= BE -AF;
故答案为: ∠α+ ∠BCA = 180° ;
(2)EF、BE、AF的数量关系:EF=BE+AF,理由如下
∵∠BEC =∠CFA =∠α, ∠α= ∠BCA,
又∵∠EBC +∠BCE+∠BEC = 180° , ∠BCE+∠ACF+∠ACB =180° ,
∴∠EBC +∠BCE =∠BCE+∠ACF
∴∠EBC = ∠ACF,
在△BEC和△CFA中
∴△ABE≌△CFA(AAS)
∴AF = CE,BE = CF
∵EF= CE+CF,
∴EF= BE+AF.
【点睛】本题考查了全等三角形的性质和判定,证明△BCE≌△CAF是解题的关键.
14.如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(点D不与点B、C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.
(1)当∠BDA=105°时,∠EDC= °,∠DEC= °;点D从点B向点C运动时,∠BDA逐渐变 .(填“大”或“小”)。(2)当DC等于多少时,△ABD≌△DCE?请说明理由.
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数;若不可以,请说明理由.
【答案】(1),小;(2)2,理由见解析;(3)或80°
【分析】(1)根据已知条件, 三角形内角和定理和平角的定义,可得,,进而可得∠EDC,∠DEC,根据题意,可得当点D从点B向点C运动时,逐渐变大,根据三角形内角和定理,即可得∠BDA逐渐变小;
(2)由(1)可得,,只要,即可证明,进而可得;
(3)根据题意,分为顶角和底角两种情况讨论,进而计算的度数.
【详解】(1),,
,
,
,
,
,,
当∠BDA=105°时,
∠EDC=,
∠DEC=;
当点D从点B向点C运动时,逐渐变大,,则∠BDA逐渐变小,
故答案为:,小;
(2),,
当时,
(AAS),
,
(3)△ADE的形状可以是等腰三角形,或,
,
,
①当时,,
,
;
②当时,,
,
,
③当时,,
,
此时点与点重合,
由题意可知点D不与点B、C重合,
此种情况不存在,
综上所述,当△ADE是等腰三角形时,或.
【点睛】本题考查了全等三角形的性质与判定,等腰三角形的性质与判定,三角形的外角性质,三角形的内角和定理,分了他了是解题的关键.
15.如图,等腰直角△ABC中,BC=AC,∠ACB=90°,现将该三角形放置在平面直角坐标系中,点B坐标为(0,2),点C坐标为(6,0).
(1)过点A作AD⊥x轴,求OD的长及点A的坐标;
(2)连接OA,若Р为坐标平面内不同于点A的点,且以O、P、C为顶点的三角形与△OAC全等,请直接写出满足条件的点P的坐标;
(3)已知OA=10,试探究在x轴上是否存在点Q,使△OAQ是以OA为腰的等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
【答案】(1)OD=8,点A的坐标(8,6);(2)(8,-6)或(-2,6)或(-2,-6);(3)(16,0)或(10,0)或(-10,0)
【分析】(1)通过证明△BOC≌△CDA,可得CD=OB=2,即可求OD的长,进而即可得到A的坐标;
(2)分三种情况:①作△OAC关于x轴的对称图形得到△OP1C;作△OAC关于直线x=3的对称图形得到△OP2C;③作△OP2C关于x轴的对称图形得到△OP3C,分别求解,即可;
(3)分三种情况:①当以点A为顶角顶点时,且OA是腰;②当以点A为底角顶点时,且OA是腰,形成锐角三角形时;③当以点A为底角顶点时,且OA是腰,形成钝角三角形时,分别求解即可.
【详解】解:(1)∵点B坐标为(0,2),点C坐标为(6,0),∴OB=2,OC=6,
∵∠ACB=90°,∴∠BCO+∠ACD=90°,且∠BCO+∠OBC=90°,
∴∠ACD=∠OBC,且AC=BC,∠BOC=∠ADC=90°,
∴△BOC≌△CDA(AAS),∴CD=OB=2,∴OD=OC+CD=8,AD=OC=6,∴点A的坐标(8,6);
(2)①作△OAC关于x轴的对称图形得到△OP1C,∴△OAC△OP1C,∴P1(8,-6);
②∵点O,C关于直线x=3对称,∴作△OAC关于直线x=3的对称图形得到△OP2C,
∴△OAC△CP2O,∴P2(-2,6);
③作△OP2C关于x轴的对称图形得到△OP3C,
∴△OP2C△OP3C,即:△OP3C△OCA,∴P3(-2,-6),
综上所述:P的坐标为:(8,-6)或(-2,6)或(-2,-6);
(3)①当以点A为顶角顶点时,且OA是腰,
∵AD⊥x轴,∴点Q1,O关于直线AD对称,即:Q1(16,0);
②当以点A为底角顶点时,且OA是腰,形成锐角三角形时,
则OQ2=OA=10,∴Q2(10,0);
③当以点A为底角顶点时,且OA是腰,形成钝角三角形时,
则OQ3=OA=10,∴Q2(-10,0),
综上所述:Q的坐标为:(16,0)或(10,0)或(-10,0).
【点睛】本题考查了全等三角形的判定和性质,坐标与图形性质,等腰三角形的性质等知识,灵活运用这些性质进行推理,掌握分类讨论思想方法是本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
