浙教版八年级上全等模型专题3——手拉手模型(含解析)
文档属性
| 名称 | 浙教版八年级上全等模型专题3——手拉手模型(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 9.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-07 20:12:33 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
全等模型专题3——手拉手模型
全等三角形在中考数学几何模块中占据着重要地位,也是学生必须掌握的一块内容,本专题就全等三角形中的重要模型(手拉手(旋转)模型)进行梳理及对应试题分析,方便掌握。
模型1.手拉手模型(三角形)
【模型解读】
将两个三角形绕着公共顶点(即头)旋转某一角度后能完全重合,则这两个三角形构成手拉手全等,也叫旋转型全等,常用“边角边”判定定理证明全等。
公共顶点A记为“头”,每个三角形另两个顶点逆时针顺序数的第一个顶点记为“左手”,第二个顶点记为“右手”。
对应操作:左手拉左手(即连结BD),右手拉右手(即连结CE),得。
【常见模型及证法】
(等边)
(等腰直角)
(等腰)
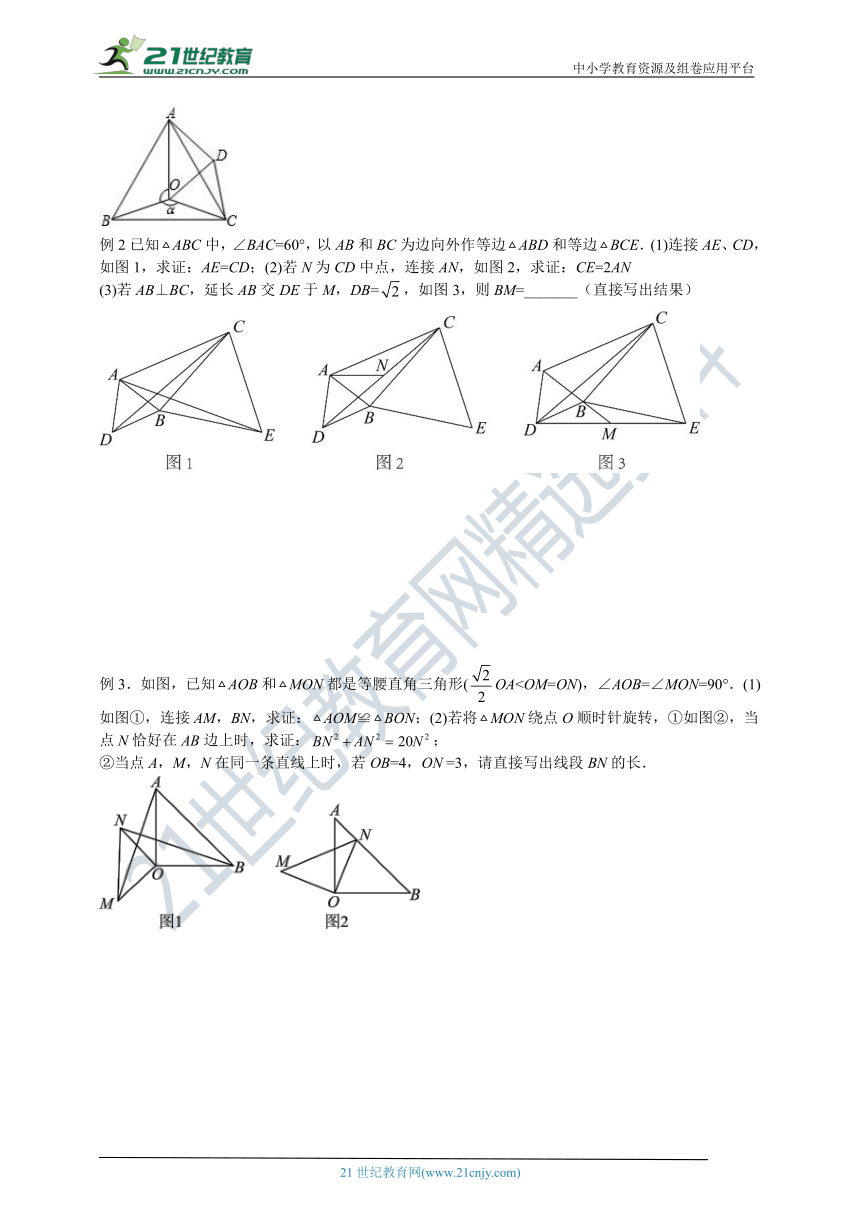
例1.如图,点O是等边三角形ABC内的一点,,将△BOC绕点C顺时针旋转60°得△ADC,连接OD.(1)当时, °;(2)当时, °;(3)若,,,则OA的长为 .
例2已知ABC中,∠BAC=60°,以AB和BC为边向外作等边ABD和等边BCE.(1)连接AE、CD,如图1,求证:AE=CD;(2)若N为CD中点,连接AN,如图2,求证:CE=2AN
(3)若AB⊥BC,延长AB交DE于M,DB=,如图3,则BM=_______(直接写出结果)
例3.如图,已知AOB和MON都是等腰直角三角形(OA②当点A,M,N在同一条直线上时,若OB=4,ON =3,请直接写出线段BN的长.
例4.在正方形中,点是边上的中点,连接,.
(1)如图1,过点作交的延长线于点,连接,求的面积;
(2)如图2,点是延长线上的一点,连接,过点作,,连接.点是的中点,分别连接,,求证:;
(3)如图3,点是直线上的一动点,连接,过点作,,连接.点是的中点,连接,.当的值最小时,直接写出的面积.
例5.综合与实践:已知是等腰三角形,.
(1)特殊情形:如图1,当∥时,______.(填“>”“<”或“=”);(2)发现结论:若将图1中的绕点顺时针旋转()到图2所示的位置,则(1)中的结论还成立吗?请说明理由.(3)拓展运用:某学习小组在解答问题:“如图3,点是等腰直角三角形内一点,,且,,,求的度数”时,小明发现可以利用旋转的知识,将绕点顺时针旋转90°得到△CAE,连接,构造新图形解决问题.请你根据小明的发现直接写出的度数.
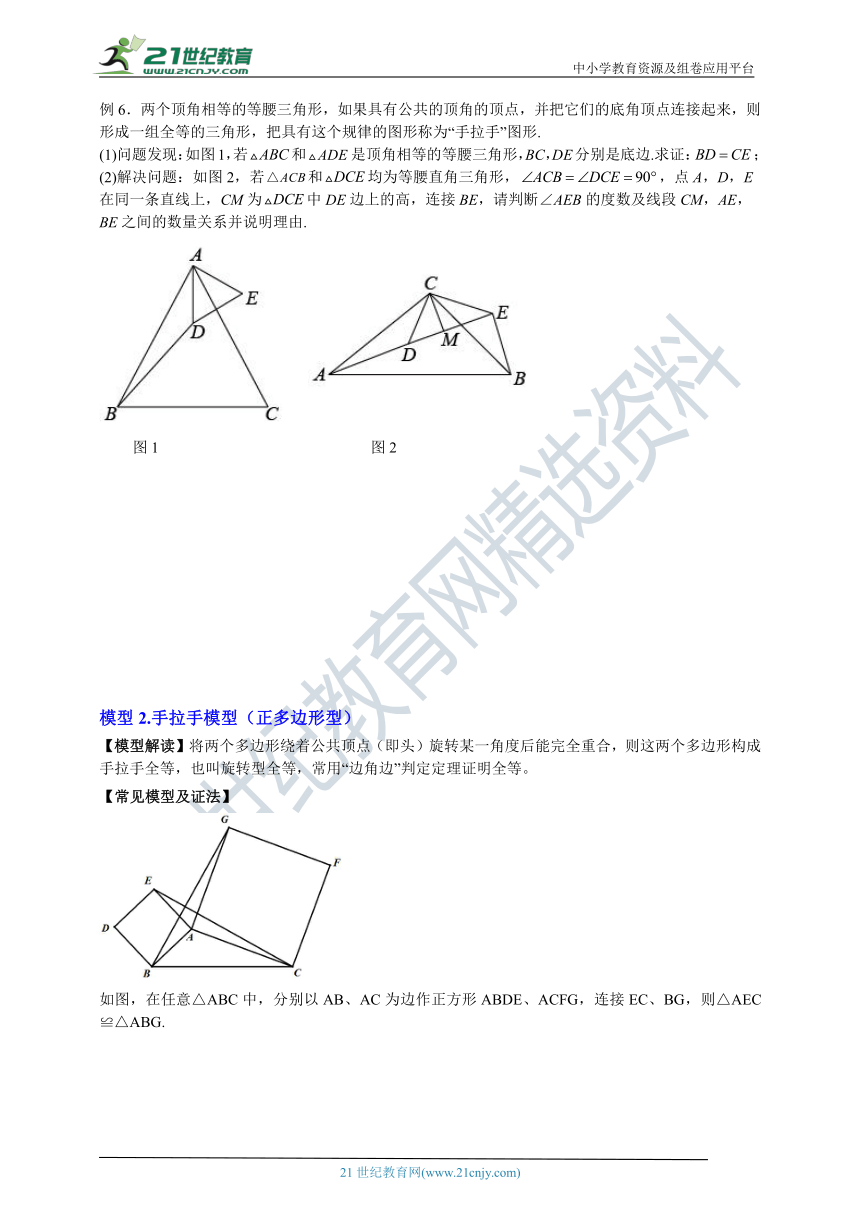
例6.两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,把具有这个规律的图形称为“手拉手”图形.
(1)问题发现:如图1,若和是顶角相等的等腰三角形,BC,DE分别是底边.求证:;
(2)解决问题:如图2,若和均为等腰直角三角形,,点A,D,E在同一条直线上,CM为中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系并说明理由.
图1 图2
模型2.手拉手模型(正多边形型)
【模型解读】将两个多边形绕着公共顶点(即头)旋转某一角度后能完全重合,则这两个多边形构成手拉手全等,也叫旋转型全等,常用“边角边”判定定理证明全等。
【常见模型及证法】
如图,在任意△ABC中,分别以AB、AC为边作正方形ABDE、ACFG,连接EC、BG,则△AEC≌△ABG.
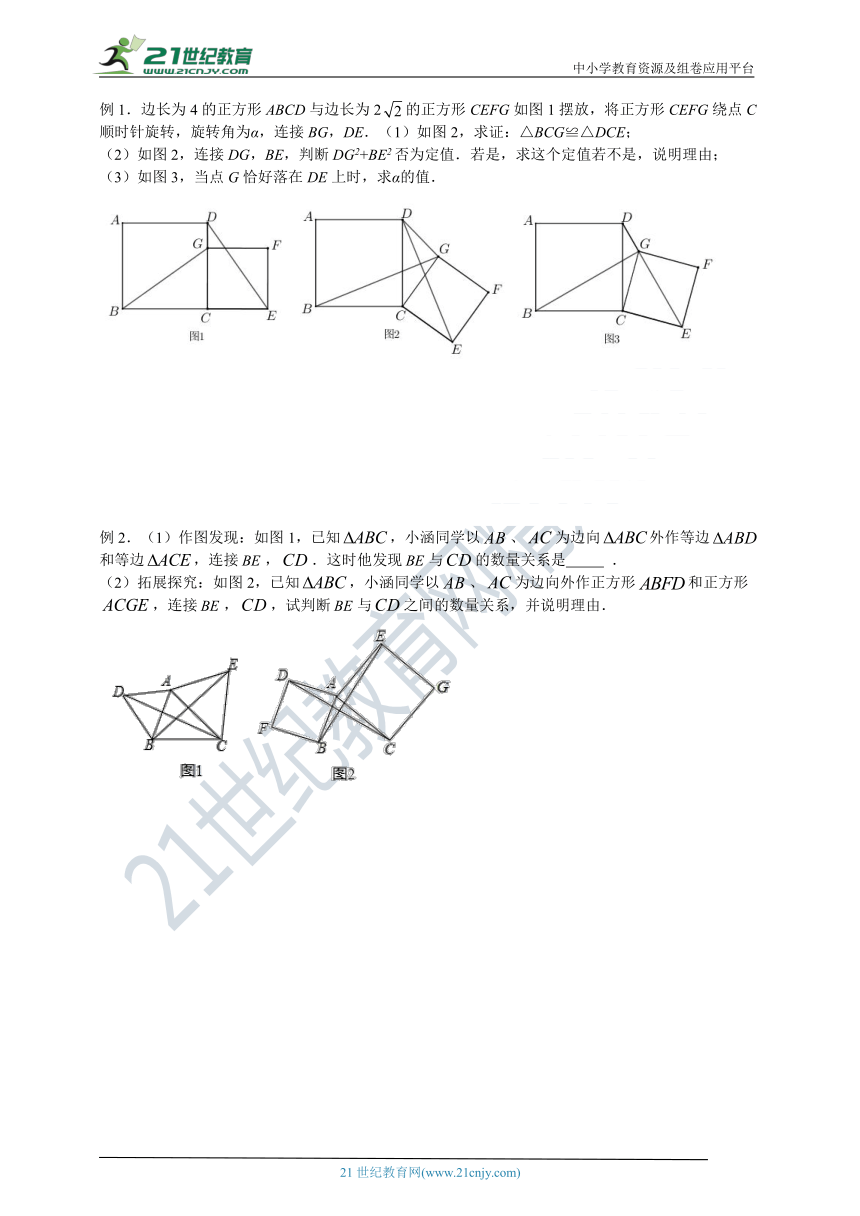
例1.边长为4的正方形ABCD与边长为2的正方形CEFG如图1摆放,将正方形CEFG绕点C顺时针旋转,旋转角为α,连接BG,DE.(1)如图2,求证:△BCG≌△DCE;
(2)如图2,连接DG,BE,判断DG2+BE2否为定值.若是,求这个定值若不是,说明理由;
(3)如图3,当点G恰好落在DE上时,求α的值.
例2.(1)作图发现:如图1,已知,小涵同学以、为边向外作等边和等边,连接,.这时他发现与的数量关系是 .
(2)拓展探究:如图2,已知,小涵同学以、为边向外作正方形和正方形,连接,,试判断与之间的数量关系,并说明理由.
例3.如图,和均为等边三角形,连接BE、CD.
(1)请判断:线段BE与CD的大小关系是 ;
(2)观察图,当和分别绕点A旋转时,BE、CD之间的大小关系是否会改变
(3)观察如图和4,若四边形ABCD、DEFG都是正方形,猜想类似的结论是________,在如图中证明你的猜想.
(4)这些结论可否推广到任意正多边形(不必证明),如图,BB1与EE1的关系是 ;它们分别在哪两个全等三角形中 ;请在如图中标出较小的正六边形AB1C1D1E1F1的另五个顶点,连接图中哪两个顶点,能构造出两个全等三角形?
例4.如图1,图2,图3,在中,分别以为边,向外作正三角形,正四边形,正五边形,相交于点.(正多边形的各边相等,各个内角也相等)
①如图1,求证:△ABE≌△ADC;②探究:如图1,∠BOD= ;
③如图2,∠BOD= ;④如图3,∠BOD= .
课后专项训练
1.如图,在△ABC中以AC,BC为边向外作正方形ACFG与正方形BCDE,连结DF,并过C点作CH⊥AB于H并交FD于M.若∠ACB=120°,AC=3,BC=2,则MD的长为( )
A. B. C. D.
第1题图 第2题图
2.如图,在中,,D是边上的一个动点,连接,并将线段绕点A逆时针旋转后得线段,连接,在点D运动过程中,线段长度的最小值是_________.
3.已知:如图,在△ABC中,AB=AC,在△ADE中,AD=AE,且∠BAC=∠DAE,连接BD,CE交于点F,连接AF.(1)求证:△ABD≌△ACE;(2)求证:FA平分∠BFE.
4.△ABC中,,,点在边上,将线段逆时针旋转得到,连接.
(1)当,时,求证:.(2)当,时,若,求的值.
5.已知:在△ABC中,CA=CB,∠ACB=90 ,D为△ABC外一点,且满足∠ADB=90°.(1)如图1,若,AD=1,求DB的长.(2)如图1,求证:.
(3)如图2所示,过C作CE⊥AD于E,BD=2,AD=6,求CE的长.
6.(1)如图1,在中,,,,则与的数量关系是 ,与延长线的夹角 ;(2)如图2,四边形中,,,,连接,猜想、、之间的数量关系,并证明你的猜想;(3)如图3,四边形中,,,,,,请直接写出的长为 .
7.如图,D为内一点,,,将绕着点A顺时针旋转能与线段重合.
(1)求证:;(2)若,求的度数.
8.两个顶角相等的等腰三角形,如果具有公共的顶角顶点,并将它们的底角顶点分别对应连接起来得到两个全等三角形,我们把这样的图形称为“手拉手”图形.如图1,在“手拉手”图形中,AB=AC,AD=AE,∠BAC=∠DAE,连接BD,CE,则△ABD≌△ACE.
(1)请证明图1的结论成立;(2)如图2,△ABC和△AED是等边三角形,连接BD,EC交于点O,求∠BOC的度数;(3)如图3,AB=BC,∠ABC=∠BDC=60°,试探究∠A与∠C的数量关系.
9.如图1,在Rt△ABC中,∠B=90°,AB=BC=4,点D,E分别为边AB,BC上的中点,且BD=BE=.
(1)如图2,将△BDE绕点B逆时针旋转任意角度α,连接AD,EC,则线段EC与AD的关系是 ;
(2)如图3,DE∥BC,连接AE,判断△EAC的形状,并求出EC的长;
(3)继续旋转△BDE,当∠AEC=90°时,请直接写出EC的长.
10.(1)如图1,在中,,,点D,E分别在边CA,CB上,且,连接AE,BD,F为AE的中点,连接CF交BD于点G,则线段CF所在直线与线段BD所在直线的位置关系是_______,线段CF和线段BD的数量关系为______.(2)将绕点C逆时针旋转至图2所示位置时,(1)中的结论是否仍然成立 若成立,请给出证明;若不成立,请说明理由.
(3)将绕点C逆时针在平面内旋转,在旋转过程中,当B,D,E三点在同一条直线上时,CF的长为________.
11.【问题背景】如图1,P是等边三角形ABC外一点,∠APB=30°,则PA2+PB2=PC2.小明为了证明这个结论,将△PAB绕点A逆时针旋转60°,请根据此思路完成其证明.
【迁移应用】如图2,在等腰直角三角形ABC中,BA=BC,∠ABC=90°,点P在△ABC外部,且∠BPC=45°,若△APC的面积为5.5,求PC.
12.问题发现:如图,在中,,为边所在直线上的动点(不与点、重合),连结,以为边作,且,根据,得到,结合,得出,发现线段与的数量关系为,位置关系为;
(1)探究证明:如图,在和中,,,且点在边上滑动(点不与点、重合),连接.①则线段,,之间满足的等量关系式为____ ;②求证: ;(2)拓展延伸:如图,在四边形中,.若,,求的长.
13.综合与实践:
【问题情景】综合与实践课上,王老师让同学们以“共顶点的等腰三角形的旋转”为主题开展数学探究活动.
【实践操作】王老师让同学们先画出两个等边和,将绕点旋转到某一位置,要求同学们观察图形,提出问题并加以解决.
(1)如图①,“慎思组”的同学们连接、,则与有何数量关系?与有何数量关系?请你探究后直接写出结论.
(2)如图②,得知“慎思组”的结论后,“博学组”的同学们又连接,他们认为,如果,且,,就可以求出的长,请写出求解过程.
【类比探究】(3)如图③,“智慧组”的同学们画出了两个等腰直角三角形和,其中,,;且点恰好落在上,那么、和之间一定存在某种数量关系,请你探究后直接写出它们之间的数量关系.
14.【问题发现】(1)如图1,△ABC和△ADE均为等边三角形,点B,D,E在同一直线上,连接,容易发现:①的度数为 ;②线段、之间的数量关系为 ;
【类比探究】(2)如图2,△ABC和△ADE均为等腰直角三角形,,点B,D,E在同一直线上,连接,试判断 的度数以及线段、、之间的数量关系,并说明理由;
【问题解决】(3)如图3,,,,,则的值为 .
15.如图甲,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.解答下列问题
(1)如果AB=AC,∠BAC=90°,①当点D在线段BC上时(与点B不重合),如图乙,线段CF、BD之间的位置关系为 ,数量关系为 .②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?(2)如果AB≠AC,∠BAC≠90°点D在线段BC上运动.试探究:当△ABC满足一个什么条件时,CF⊥BC(点C、F重合除外)?并说明理由.
16.正方形ABCD和正方形AEFG的边长分别为3和1,将正方形AEFG绕点A逆时针旋转.
(1)当旋转至图1位置时,连接BE,DG,则线段BE和DG的关系为 ;
(2)在图1中,连接BD,BF,DF,求在旋转过程中BDF的面积最大值;
(3)在旋转过程中,当点G,E,D在同一直线上时,求线段BE的长.
八年级全等模型专题3—— 手拉手模型
全等三角形在中考数学几何模块中占据着重要地位,也是学生必须掌握的一块内容,本专题就全等三角形中的重要模型(手拉手(旋转)模型)进行梳理及对应试题分析,方便掌握。
模型1.手拉手模型(三角形)
【模型解读】
将两个三角形绕着公共顶点(即头)旋转某一角度后能完全重合,则这两个三角形构成手拉手全等,也叫旋转型全等,常用“边角边”判定定理证明全等。
公共顶点A记为“头”,每个三角形另两个顶点逆时针顺序数的第一个顶点记为“左手”,第二个顶点记为“右手”。
对应操作:左手拉左手(即连结BD),右手拉右手(即连结CE),得。
【常见模型及证法】
(等边)
(等腰直角)
(等腰)
例1.(2022秋·吉林松原·九年级统考期中)如图,点O是等边三角形ABC内的一点,,将△BOC绕点C顺时针旋转60°得△ADC,连接OD.(1)当时, °;(2)当时, °;(3)若,,,则OA的长为 .
【答案】(1)40; (2)60;(3)
【分析】(1)证明△COD是等边三角形,得到∠ODC=60°,即可得到答案;
(2)利用∠ADC-∠ODC求出答案;(3)由△BOC≌△ADC,推出∠ADC=∠BOC=150°,AD=OB=8,根据△COD是等边三角形,得到∠ODC=60°,OD=,证得△AOD是直角三角形,利用勾股定理求出.
【详解】(1)解:∵CO=CD,∠OCD=60°,∴△COD是等边三角形;∴∠ODC=60°,
∵∠ADC=∠BOC=,∴∠ADC-∠ODC=40°,故答案为:40;
(2)∵∠ADC=∠BOC=,∴∠ADC-∠ODC=60°,故答案为:60;
(3)解:当,即∠BOC=150°,∴△AOD是直角三角形.
∵△BOC≌△ADC,∴∠ADC=∠BOC=150°,AD=OB=8,
又∵△COD是等边三角形,∴∠ODC=60°,OD=,∴∠ADO=90°,
即△AOD是直角三角形,∴,故答案为:.
【点睛】本题以“空间与图形”中的核心知识(如等边三角形的性质、全等三角形的性质与证明、直角三角形的判定、多边形内角和等)为载体,内容由浅入深,层层递进.试题中几何演绎推理的难度适宜,蕴含着丰富的思想方法(如运动变化、数形结合、分类讨论、方程思想等),能较好地考查学生的推理、探究及解决问题的能力.
例2.(2022·湖北武汉·八年级期末)已知ABC中,∠BAC=60°,以AB和BC为边向外作等边ABD和等边BCE.(1)连接AE、CD,如图1,求证:AE=CD;(2)若N为CD中点,连接AN,如图2,求证:CE=2AN
(3)若AB⊥BC,延长AB交DE于M,DB=,如图3,则BM=_______(直接写出结果)
【答案】(1)见解析(2)见解析(3)
【分析】(1)先判断出∠DBC=∠ABE,进而判断出△DBC≌△ABE,即可得出结论;
(2)先判断出△ADN≌△FCN,得出CF=AD,∠NCF=∠AND,进而判断出∠BAC=∠ACF,即可判断出△ABC≌△CFA,即可得出结论;(3)先判断出△ABC≌△HEB(ASA),得出,,再判断出△ADM≌△HEM (AAS),得出AM=HM,即可得出结论.
(1)解:∵△ABD和△BCE是等边三角形,∴BD=AB,BC=BE,∠ABD=∠CBE=60°,
∴∠ABD+∠ABC=∠CBE+∠ABC,∴∠DBC=∠ABE,∴△ABE≌△DBC(SAS),∴AE=CD;
(2)解:如图,延长AN使NF=AN,连接FC,
∵N为CD中点,∴DN=CN,
∵∠AND=∠FNC,∴△ADN≌△FCN(SAS),∴CF=AD,∠NCF=∠AND,
∵∠DAB=∠BAC=60°∴∠ACD +∠ADN=60°
∴∠ACF=∠ACD+∠NCF=60°,∴∠BAC=∠ACF,
∵△ABD是等边三角形,∴AB=AD,∴AB=CF,
∵AC=CA,∴△ABC≌△CFA (SAS),∴BC=AF,
∵△BCE是等边三角形,∴CE=BC=AF=2AN;
(3)解: ∵△ABD是等边三角形,∴,∠BAD=60°,
在Rt△ABC中,∠ACB=90°-∠BAC=30°,∴,
如图,过点E作EH // AD交AM的延长线于H,
∴∠H=∠BAD=60°,∵△BCE是等边三角形,∴BC=BE,∠CBE=60°,
∵∠ABC=90°,∴∠EBH=90°-∠CBE=30°=∠ACB,
∴∠BEH=180°-∠EBH-∠H=90°=∠ABC,
∴△ABC≌△HEB (ASA),∴,,∴AD=EH,
∵∠AMD=∠HME,∴△ADM≌△HEM (AAS),∴AM=HM,
∴
∵,,∴.故答案为:.
【点睛】此题是三角形综合题,主要考查了等边三角形的性质,含30°角的直角三角形的性质,全等三角形的判定和性质,构造出全等三角形是解本题的关键.
例3.(2022·湖北·襄阳市九年级阶段练习)如图,已知AOB和MON都是等腰直角三角形(OA②当点A,M,N在同一条直线上时,若OB=4,ON =3,请直接写出线段BN的长.
【答案】(1)见解析;(2)①见解析;②或.
【分析】(1)利用SAS定理证明即可;
(2)①连接,证明,即可证;②当点N在线段上时,连接,在中构造勾股定理的等量关系;当点M在线段上时,同理即可求得.
(1)证明:,,即.
和是等腰直角三角形,,(SAS) .
(2)解:①证明:如图,连接.
,,即.
和是等腰直角三角形,,
,,.
是等腰直角三角形,,.
②或.∵△AOB和△MON都是等腰直角三角形,OB=4,ON =3,∴.
当点N在线段上时,如图,连接,设,
由(1)可知.∴,.
∴,
∴,∴是直角三角形,.
又∵,∴,
解得:(舍去)∴;
当点M在线段上时,如图,连接,设,由(2)①可知.
∴,.
∴,
∴,∴是直角三角形,.
又∵,∴,
解得: (舍去)∴
综上所述:的长为或.
【点睛】本题主要考查全等三角形的判定与性质、等腰直角三角形的性质,三点共线分类讨论,对几何题目的综合把握是解题关键.
例4.(2023春·重庆巴南·八年级统考期末)在正方形中,点是边上的中点,连接,.
(1)如图1,过点作交的延长线于点,连接,求的面积;
(2)如图2,点是延长线上的一点,连接,过点作,,连接.点是的中点,分别连接,,求证:;
(3)如图3,点是直线上的一动点,连接,过点作,,连接.点是的中点,连接,.当的值最小时,直接写出的面积.
【答案】(1)(2)证明见解析(3)
【分析】(1)利用证明得,从而求出,由此即可求出的面积.(2)过点作交于点,连接,利用一线三直角模型可得(),从而可得:,再证明可得为等腰直角三角形,,进而得出结论;(3)由已知可得:是等腰直角三角形,进而可得,,即当E点在AM上时,最小,再由三角形全都转换线段关系得到,由勾股定理求出即可解题.
【详解】(1)解:∵;∴;
∵四边形是正方形;∴,;
∵点是的中点,;∴;
∵;
∴;∴;∴;
∴;
(2)证明:如解(2)图,过点作交于点,连接.
∵;∴∴;
∵;∴;∴,;
∵点是的中点,;∴,:
∴;∴;∴,;
∴;∴;∴;
(3)解:∵,,∴是等腰直角三角形,,
又∵点是的中点,∴,∴,
∴当E点在上时,最小,如解(3)图,过点作交的延长线于点,
同理(1)可得:;∴;,,
∴,
又∵∴,
又∵,∴,∴,
∴,
在中,,,
∴,解得:,∴
【点睛】本题主要考查了正方形的性质与判定,勾股定理,全等三角形的性质与判定,解题(3)的关键在于能够证明.
例5.(2022·山西大同·九年级期中)综合与实践:已知是等腰三角形,.
(1)特殊情形:如图1,当∥时,______.(填“>”“<”或“=”);(2)发现结论:若将图1中的绕点顺时针旋转()到图2所示的位置,则(1)中的结论还成立吗?请说明理由.(3)拓展运用:某学习小组在解答问题:“如图3,点是等腰直角三角形内一点,,且,,,求的度数”时,小明发现可以利用旋转的知识,将绕点顺时针旋转90°得到,连接,构造新图形解决问题.请你根据小明的发现直接写出的度数.
【答案】(1)=;(2)成立,理由见解析;(3)∠BPA=135°.
【分析】(1)由DE∥BC,得到∠ADE=∠B,∠AED=∠C,结合AB=AC,得到DB=EC;
(2)由旋转得到的结论判断出△DAB≌△EAC,得到DB=CE;(3)由旋转构造出△APB≌△AEC,再用勾股定理计算出PE,然后用勾股定理逆定理判断出△PEC是直角三角形,在简单计算即可.
【详解】解:(1)∵DE∥BC,∴∠ADE=∠B,∠AED=∠C,
∵AB=AC,∴∠B=∠C,∴∠ADE=∠AED,∴AD=AE,∴DB=EC,故答案为:=;
(2)成立.证明:由①易知AD=AE,∴由旋转性质可知∠DAB=∠EAC,
在△DAB和△EAC中,∴△DAB≌△EAC(SAS),∴DB=CE;
(3)如图,
将△APB绕点A旋转90°得△AEC,连接PE,∴△APB≌△AEC,
∴AE=AP=2,EC=BP=1,∠PAE=90°,∴∠AEP=∠APE=45°,
在Rt△PAE中,由勾股定理可得,PE=2,
在△PEC中,PE2=(2)2=8,CE2=12=1,PC2=32=9,
∵PE2+CE2=PA2,∴△PEC是直角三角形,∴∠PEC=90°,∴∠AEC=135°,
又∵△APB≌△AEC,∴∠BPA=∠CEA=135°.
【点睛】本题主要考查了旋转的性质,平行线的性质,全等三角形的性质和判定,勾股定理及其逆定理,解本题的关键是构造全等三角形,也是本题的难点.
例6.(2022·青海·中考真题)两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,把具有这个规律的图形称为“手拉手”图形.
(1)问题发现:如图1,若和是顶角相等的等腰三角形,BC,DE分别是底边.求证:;
(2)解决问题:如图2,若和均为等腰直角三角形,,点A,D,E在同一条直线上,CM为中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系并说明理由.
图1 图2
【答案】(1)见解析 (2);
【分析】(1)先判断出∠BAD=∠CAE,进而利用SAS判断出△BAD≌△CAE,即可得出结论;
(2)同(1)的方法判断出△BAD≌△CAE,得出AD=BE,∠ADC=∠BEC,最后用角的差,即可得出结论.
【解析】(1)证明:∵和是顶角相等的等腰三角形,
∴,,,
∴,∴.
在和中,,∴,∴.
(2)解:,,
理由如下:由(1)的方法得,,∴,,
∵是等腰直角三角形,∴,
∴,∴,
∴.
∵,,∴.∵,∴,
∴.∴.
【点睛】此题是三角形综合题,主要考查了全等三角形的判定和性质,等腰三角形,等边三角形,等腰直角三角形的性质,判断出△ACD≌△BCE是解本题的关键.
模型2.手拉手模型(正多边形型)
【模型解读】将两个多边形绕着公共顶点(即头)旋转某一角度后能完全重合,则这两个多边形构成手拉手全等,也叫旋转型全等,常用“边角边”判定定理证明全等。
【常见模型及证法】
如图,在任意△ABC中,分别以AB、AC为边作正方形ABDE、ACFG,连接EC、BG,则△AEC≌△ABG.
例1.(2023春·浙江·八年级专题练习)边长为4的正方形ABCD与边长为2的正方形CEFG如图1摆放,将正方形CEFG绕点C顺时针旋转,旋转角为α,连接BG,DE.
(1)如图2,求证:△BCG≌△DCE;
(2)如图2,连接DG,BE,判断DG2+BE2否为定值.若是,求这个定值若不是,说明理由;
(3)如图3,当点G恰好落在DE上时,求α的值.
【答案】(1)见解析;(2)48;(3)
【分析】(1)通过边角边判定三角形全等;(2)连接,设交于点,交于点,先证明,由勾股定理可得;(3)作于点,则,且,由含30度角的直角三角形的性质求解.
【详解】(1)四边形与为正方形,,,
,,,
在和中, (SAS),
(2)连接,设交于点,交于点,
,,,
在△和中,,
,,
,
由勾股定理得,,
,
,,,,
(3)作于点,如图,
△为等腰直角三角形,,且,
在中,,,,
..
【点睛】本题考查四边形与三角形的综合问题,解题关键是熟练掌握正方形与直角三角形的性质,通过添加辅助线求解.
例2.(2023·河南鹤壁市八年级月考)(1)作图发现:如图1,已知,小涵同学以、为边向外作等边和等边,连接,.这时他发现与的数量关系是 .
(2)拓展探究:如图2,已知,小涵同学以、为边向外作正方形和正方形,连接,,试判断与之间的数量关系,并说明理由.
【答案】(1)BE=CD;(2)BE=CD,理由见解析;
【分析】(1)利用等边三角形的性质得出,然后有,再利用SAS即可证明,则有;
(2)利用正方形的性质得出,然后有,再利用SAS即可证明,则有;
【详解】(1)如图1所示:
和都是等边三角形,,
,即,
在和中,,.
(2),四边形和均为正方形,
,,,
,
在和中,,,
例3.(2023·福建福州市·九年级月考)如图,和均为等边三角形,连接BE、CD.
(1)请判断:线段BE与CD的大小关系是 ;
(2)观察图,当和分别绕点A旋转时,BE、CD之间的大小关系是否会改变
(3)观察如图和4,若四边形ABCD、DEFG都是正方形,猜想类似的结论是________,在如图中证明你的猜想.
(4)这些结论可否推广到任意正多边形(不必证明),如图,BB1与EE1的关系是 ;它们分别在哪两个全等三角形中 ;请在如图中标出较小的正六边形AB1C1D1E1F1的另五个顶点,连接图中哪两个顶点,能构造出两个全等三角形?
【答案】(1) BE=CD (2)线段BE与CD的大小关系不会改变 (3)AE=CG,证明见解析 (4)这些结论可以推广到任意正多边形.如图5,BB1=EE1,它们分别在△AE1E和△AB1B中,如图6,连接FF1,可证△AB1B≌△AF1F.图形见解析.
【分析】本题是变式拓展题,图形由简单到复杂,需要从简单图形中探讨解题方法,并借鉴用到复杂图形中;证明三角形全等时,用旋转变换寻找三角形全等的条件.
【详解】(1)线段BE与CD的大小关系是BE=CD;(2)线段BE与CD的大小关系不会改变;
(3)AE=CG.证明:如图4,正方形ABCD与正方形DEFG中,∵AD=CD,DE=DG,∠ADC=∠GDE=90°,
又∠CDG=90°+∠ADG=∠ADE,∴△ADE≌△CDG,∴AE=CG.
(4)这些结论可以推广到任意正多边形.
如图5,BB1=EE1,它们分别在△AE1E和△AB1B中,如图6,连接FF1,可证△AB1B≌△AF1F.
【点睛】本题综合考查全等三角形、等边三角形和多边形有关知识.注意对三角形全等的证明方法的发散.
例4.(2023·江苏无锡·八年级校考阶段练习)如图1,图2,图3,在中,分别以为边,向外作正三角形,正四边形,正五边形,相交于点.(正多边形的各边相等,各个内角也相等)
①如图1,求证:△ABE≌△ADC;②探究:如图1,∠BOD= ;
③如图2,∠BOD= ;④如图3,∠BOD= .
【答案】①见解析;②60°;③90°;④108°
【分析】①根据等边三角形的性质可以得出△ABE≌△ADC.
②③④根据△ABE≌△ADC可得∠CDA=∠EBA,根据三角形内角和可得∠BOD=∠BAD,从而求解.
【详解】解:①证明:如图,
∵△ABD和△AEC是等边三角,∴AD=AB,AE=AC,∠DAB=∠EAC=∠ABD=∠ADB=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,即∠DAC=∠BAE.
在△ABE和△ADC中,,∴△ABE≌△ADC(SAS);
②,,∵∠AFD=∠OFB,∴∠BOD=∠BAD=60°;
③如图, 四边形和四边形是正方形,
,,,,
,即,
在和中,,,,
∵∠AHB=∠OHD,∴∠BOD=∠BAD=90°;
④如图,五边形和五边形是正五边形,
,,,
,,,
在和中,,,,
∵∠AMB=∠OMD,∴∠BOD=∠BAD=(5-2)×180°÷5=108°.
【点睛】本题考查了等边三角形的性质的运用,正方形的性质的运用,正五边形的性质的运用及正边形的性质的运用,全等三角形的判定及性质的运用,解答时根据正多边形的性质证明三角形全等是关键.
课后专项训练
1.(2022·浙江·温州一模)如图,在△ABC中以AC,BC为边向外作正方形ACFG与正方形BCDE,连结DF,并过C点作CH⊥AB于H并交FD于M.若∠ACB=120°,AC=3,BC=2,则MD的长为( )
A. B. C. D.
【答案】A
【分析】过D作DN⊥CF于点N,作DP⊥HM于点P,过点F作FQ⊥HM,交HM的延长线于点Q,依据勾股定理即可求得DF的长,再根据全等三角形的对应边相等得到FQ=DP,进而证明
△FQM≌△DPM,得到M是FD的中点,由此可得DM=DF.
【详解】如图所示,过D作DN⊥CF于点N,作DP⊥HM于点P,过点F作FQ⊥HM,交HM的延长线于点Q,
∵∠ACB=120°,∠ACF=∠BCD=90°,∴∠DCN=60°,∠CDN=30°,
又∵BC=DC=2,AC=FC=3,
∴CNCD=1,FN=CF﹣CN=3﹣1=2,DN,
Rt△DFN中,DF.
∵四边形BCDE是正方形,∴BC=CD,∠BCD=90°,
又∵CH⊥AB,∴∠DCP+∠BCH=∠CBH+∠BCH=90°,∴∠DCP=∠CBH,
又∵∠DPC=∠BHC=90°,∴△DCP≌△CBH(AAS),
∴DP=CH,同理可得△ACH≌△CFQ,∴FQ=CH,∴FQ=DP,
又∵∠Q=∠DPM=90°,∠FMQ=∠DMP,∴△FQM≌△DPM(AAS),
∴FM=DM,即M是FD的中点,
∴DMDF.故选:A
【点睛】本题考查了正方形的性质,全等三角形的判定与性质以及勾股定理的综合运用,通过作辅助线构造全等三角形,灵活运用全等三角形的对应边相等是解题的关键.
2.(2022·广东茂名·二模)如图,在中,,D是边上的一个动点,连接,并将线段绕点A逆时针旋转后得线段,连接,在点D运动过程中,线段长度的最小值是_________.
【答案】
【分析】过点作于点,在上取点,使,连接,先根据直角三角形的性质、勾股定理可得,根据等腰直角三角形的判定与性质可得,从而可得,再根据旋转的性质可得,然后根据三角形全等的判定证出,根据全等三角形的性质可得,最后根据垂线段最短可得当时,的长度最小,在中,解直角三角形即可得.
【详解】解:如图,过点作于点,在上取点,使,连接,
,,
,是等腰直角三角形,
,,
,
由旋转的性质得:,,
,,,
在和中,,,,
如图,由垂线段最短可知,当时,的长度最小,
在中,,
即线段长度的最小值是,故答案为:.
【点睛】本题考查了含角的直角三角形的性质、勾股定理、三角形全等的判定定理与性质、旋转的性质、解直角三角形等知识点,通过作辅助线,构造全等三角形是解题关键.
3.(2022·安徽芜湖·八年级期末)已知:如图,在△ABC中,AB=AC,在△ADE中,AD=AE,且∠BAC=∠DAE,连接BD,CE交于点F,连接AF.(1)求证:△ABD≌△ACE;(2)求证:FA平分∠BFE.
【答案】(1)见解析(2)见解析
【分析】(1)根据SAS证明结论即可;(2)作AM⊥BD于M,作AN⊥CE于N.由(1)可得BD=CE,S△BAD=S△CAE,然后根据角平分线的性质即可解决问题.
【解析】(1)证明:∵∠BAC=∠DAE,
∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,
在△BAD和△CAE中,,∴△BAD≌△CAE(SAS);
(2)证明:如图,作AM⊥BD于M,作AN⊥CE于N.
由△BAD≌△CAE,∴BD=CE,S△BAD=S△CAE,
∵,∴AM=AN,
∴点A在∠BFE平分线上,∴FA平分∠BFE.
【点睛】本题考查全等三角形的判定和性质、三角形的面积,解题的关键是熟练掌握全等三角形的判定和性质,学会转化的思想,巧用等积法进行证明.
4.(2023春·八年级单元测试)中,,,点在边上,将线段逆时针旋转得到,连接.
(1)当,时,求证:.(2)当,时,若,求的值.
【答案】(1)证明见解析(2)
【分析】(1)根据题意证明,得出,,,勾股定理即可得证;(2)在的延长线上取点,使,由同理得,设,根据勾股定理得出,作于,得出是等腰直角三角形,分别求得,即可求解.
【详解】(1)证明:如图,连接,
,,
在和中,,
,,,
,,
,;
(2)在的延长线上取点,使
,由同理得,,
,设,∴
作于,,是等腰直角三角形,
∴.
【点睛】本题考查了旋转的性质,勾股定理,含30度角的直角三角形的性质,等腰直角三角形的性质,全等三角形的性质与判定,掌握旋转的性质是解题的关键.
5.(2022·福建·长汀县第四中学八年级阶段练习)已知:在△ABC中,CA=CB,∠ACB=90 ,D为△ABC外一点,且满足∠ADB=90°.
(1)如图1,若,AD=1,求DB的长.(2)如图1,求证:.
(3)如图2所示,过C作CE⊥AD于E,BD=2,AD=6,求CE的长.
【答案】(1);(2)见解析;(3)2
【分析】(1)在Rt△ABC中,根据勾股定理,得AB=2,在Rt△ABD中,根据勾股定理,得;
(2)过C点作CF⊥CD,构造手拉手模型,运用等腰直角三角形的性质可得证;
(3)过C点作CF⊥CD,构造手拉手模型,运用三角形全等可得证.
【详解】(1)解:在Rt△ABC中,∵,∴,
∴在Rt△ABD中,.
(2)证明:如图,过C点作CF⊥CD交DB的延长线于点F.
∵∠ACB=∠DCF=90°,∴∠ACD=∠BCF,
∵∠CAD+∠CBD=360°-(∠ACB+∠ADB)=180°,∠CBF+∠CBD=180°,
∴∠CAD=∠CBF,又∵CA=CB,∴△CAD≌△CBF(ASA),
∴CD=CF,AD=BF,∴,
∵DF=DB+BF=DB+DA,∴.
(3)解:如图,过C点作CF⊥CD交AD与F点,
∵∠ACB=∠DCF=90°,即∠ACF+∠BCF=∠BCD+∠BCF=90°,∴∠ACF=∠BCD,
∵∠AFC=∠FCD+∠CDA=90°+∠CDA,∠CDB=∠CDA+∠ADB=90°+∠CDA,∴∠AFC=∠CDB,
又∵CA=CB,∴△CAF≌△CBD(AAS), ∴CF=CD,AF=BD,
∴△CDF是等腰直角三角形,
又∵CE⊥AD,∴E为DF中点,
∵AD=6,AF=BD=2,∴FD=AD-AF=4,
∴.
【点睛】本题考查了勾股定理,等腰直角三角形的性质,等腰三角形的性质,三角形的全等,手拉手模型的构造,熟练构造手拉手模型是解题的关键.
6.(2023春·湖北武汉·八年级校考阶段练习)
(1)如图1,在中,,,,则与的数量关系是 ,与延长线的夹角 ;(2)如图2,四边形中,,,,连接,猜想、、之间的数量关系,并证明你的猜想;(3)如图3,四边形中,,,,,,请直接写出的长为 .
【答案】(1),(2)(3)
【分析】(1)证明≌即可.
(2)由(1)的证明方法可知:将绕点顺时针旋转, 连接、,证明≌,再为直角三角形,用勾股定理即可.
(3)由(1)的证明方法可知:将绕点顺时针旋转, 连接、,延长交于,再证明,用勾股定理即可求解.
【详解】(1)与的数量关系:,
证明:,
,,
在和中,
≌,,
故与的数量关系:;,
≌,,即:,
在中:
.故.
(2)
结论:,
证明:如图,将绕点顺时针旋转,连接、,
,,是等边三角形,,
, ,,
在和中,
≌,,,
,,
,
,
在中,.
(3)
解:如图,将绕点顺时针旋转,连接、,延长交于,
,,是等腰直角三角形,
,,,
,,
,,
在和中,
≌,
,,
,
,,
设,,则有,,
在中,,
在中,,
由①②解得,,
在中,故的长为.
【点睛】本题考查了三角形全等及性质、勾股定理在旋转中典型模型“手拉手”的综合应用,掌握典型模型的解决方法是解题的关键.
7.(2023春·广东汕头·九年级校考开学考试)如图,D为内一点,,,将绕着点A顺时针旋转能与线段重合.
(1)求证:;(2)若,求的度数.
【答案】(1)见解析(2)
【分析】(1)根据将绕着点A顺时针旋转能与线段重合,得,,通过证明,即可证出;
(2)由得:,再根据,,得,即可求出答案.
【详解】(1)证明:∵将绕着点A顺时针旋转能与线段重合,
∴,,
∵,
∴,
∴,
在和中,
,
∴,
∴;
(2)解:由得:,
∵,
∴,
∵,,
∴,
∴.
【点睛】本题主要考查了旋转的性质、等腰三角形是性质、三角形全等的判定与性质等知识,证明出是解题的关键.
8.(2023春·全国·七年级专题练习)两个顶角相等的等腰三角形,如果具有公共的顶角顶点,并将它们的底角顶点分别对应连接起来得到两个全等三角形,我们把这样的图形称为“手拉手”图形.如图1,在“手拉手”图形中,AB=AC,AD=AE,∠BAC=∠DAE,连接BD,CE,则△ABD≌△ACE.
(1)请证明图1的结论成立;
(2)如图2,△ABC和△AED是等边三角形,连接BD,EC交于点O,求∠BOC的度数;
(3)如图3,AB=BC,∠ABC=∠BDC=60°,试探究∠A与∠C的数量关系.
【答案】(1)见解析(2)60°(3)∠A+∠BCD=180°,理由见解析
【分析】(1)利用等式的性质得出∠BAD=∠CAE,即可得出结论;
(2)同(1)的方法判断出△ABD≌△ACE,得出∠ADB=∠AEC,再利用对顶角和三角形的内角和定理判断出∠BOC=60°,即可得出答案;(3)先判断出△BDP是等边三角形,得出BD=BP,∠DBP=60°,进而判断出△ABD≌△CBP(SAS),即可得出结论.
【详解】(1)解:证明:∵∠BAC=∠DAE,
∴∠BAC+∠CAD=∠DAE+∠CAD,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS);
(2)如图2,
∵△ABC和△ADE是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴∠ADB=∠AEC,
令AD与CE交于点G,
∵∠AGE=∠DGO,
∴180°-∠ADB-∠DGO=180°-∠AEC-∠AGE,
∴∠DOE=∠DAE=60°,
∴∠BOC=60°;
(3)∠A+∠BCD=180°.理由:
如图3,延长DC至P,使DP=DB,
∵∠BDC=60°,
∴△BDP是等边三角形,
∴BD=BP,∠DBP=60°,
∵∠ABC=60°=∠DBP,
∴∠ABD=∠CBP,
∵AB=CB,
∴△ABD≌△CBP(SAS),
∴∠BCP=∠A,
∵∠BCD+∠BCP=180°,
∴∠A+∠BCD=180°.
【点睛】此题是三角形综合题,主要考查了等腰三角形的性质,等边三角形的性质,全等三角形的判定和性质,构造等边三角形是解本题的关键.
9.(2022春·湖南长沙·八年级长沙市湘郡培粹实验中学校考阶段练习)如图1,在Rt△ABC中,∠B=90°,AB=BC=4,点D,E分别为边AB,BC上的中点,且BD=BE=.
(1)如图2,将△BDE绕点B逆时针旋转任意角度α,连接AD,EC,则线段EC与AD的关系是 ;
(2)如图3,DE∥BC,连接AE,判断△EAC的形状,并求出EC的长;
(3)继续旋转△BDE,当∠AEC=90°时,请直接写出EC的长.
【答案】(1)EC=AD,EC⊥AD(2)等腰三角形,(3)
【分析】(1)延长CE交AD于F,交AB于O,证明△ABD≌△CBE(SAS),得∠BCE=∠BAD,CE=AD,再由∠AOF=∠BOC,可得∠AFC=∠ABC=90°,即可得到结论;(2)设DE与AB的交点为H,可得AB是DE的垂直平分线,利用勾股定理可求出AE的长,由(1)知CE=AD,从而得出答案;(3)分当点E在BC上方时和当点E在BC下方时,分别画图,利用勾股定理计算即可.
(1)EC与AD垂直且相等,理由如下:
延长CE交AD于F,交AB于O,
∵△BDE和△ABC都是等腰直角三角形,
∴BD=BE,AB=BC,∠DBE=∠ABC=90°,
∴∠ABD=∠CBE,
∴△ABD≌△CBE(SAS),
∴∠BCE=∠BAD,CE=AD,
∵∠AOF=∠BOC,
∴∠AFE=∠ABC=90°,
∴AD⊥CE,
∴故答案为:EC=AD,EC⊥AD;
(2)设DE与AB的交点为H,
∵DE∥BC,
∴∠AHE=∠ABC=90°,
∵BD=BE,
∴AB是DE的垂直平分线,
∴AD=AE,
由(1)知AD=CE,
∴AE=CE,
∴△ACE是等腰三角形,
∵BE=,
∴BH=HE=1,
∴AH=AB﹣BH=4﹣1=3,
在Rt△AHE中,由勾股定理得:AE=,
∴CE=AE=;
(3)
如图4,当点E在BC上方时,
过点B作BG⊥DE于G,
∵∠AEC=90°,CE⊥AD,
∴A、E、D三点共线,
∴AG=,
∴AD=AG+DG=,
∴CE=AD=+1;
如图,当点E在BC下方时,
同理可得CE=CG﹣GE=﹣1.
综上:CE=+1或﹣1.
【点睛】本题主要考查了等腰直角三角形的判定与性质,全等三角形的判定与性质,旋转的性质,勾股定理等知识,根据前面探索的结论解决新的问题是解题的关键.
10.(2022·河南焦作·二模)(1)如图1,在中,,,点D,E分别在边CA,CB上,且,连接AE,BD,F为AE的中点,连接CF交BD于点G,则线段CF所在直线与线段BD所在直线的位置关系是_______,线段CF和线段BD的数量关系为______.
(2)将绕点C逆时针旋转至图2所示位置时,(1)中的结论是否仍然成立 若成立,请给出证明;若不成立,请说明理由.
(3)将绕点C逆时针在平面内旋转,在旋转过程中,当B,D,E三点在同一条直线上时,CF的长为________.
【答案】(1)CF⊥BD;
(2)(1)中的结论仍然成立.理由见解析
(3)或
【分析】(1)延长CF到点M,使得FM=CF,连接AM.证,得,,所以,推出∠MAC=∠DCB=90°,再(SAS),得,,继而得到,则,故有结论CG⊥BD,BD=2CF.
(2)延长CF至M使则,连接AM,延长BC到N,先证明,得,,再证明,得,,从而得证,得到,即可得出(1)中的结论:,BD=2CF.
(3)分两种情形:如图3中,当点E在线段BD上时,如图4中,当点E在线段BD的延长线上时,分别求解即可.
【详解】解:(1)如图,延长CF至M使,则,连接AM,
∵F是AE的中点,,且,
∴,
∴,,
∴,
∴,
∵,
∴,
又∵,
∴,
∴(SAS),
∴,
∵,
∴,
∴,
∴,
故答案为:CG⊥BD,BD=2CF.
(2)证明:(1)中的结论仍然成立.
理由如下:如图,延长CF至M,使,则,连接AM,延长BC到N,
∵F是AE的中点,,且,
∴,
∴,,
∴,
∴,
∴,
又∵,,
∴,
∵,
∴,
∴,
∴,
∴,
∴,,
∵,
∴,
∴,
∴,
∴(1)中的结论:,BD=2CF仍然成立
(3)如图3中,当点E在线段BD上时,
延长CF至M使则,连接AM,
在Rt△DCE中,CD=CE=2,
∴DE=,
∵CG⊥DE,CD=CE,
∴CG平分DE,
∵∠DCE=90°,
∴DG=CG=DE=,
在Rt△CGB中,CB=6,CG=,
∴BG=,
∴BD=BG+DG=+,
由(2)知BD=2CF,
∴ CF=BD=;
如图4中,当点E在线段BD的延长线上时,
延长CF至M使则,连接AM,
在Rt△DCE中,CD=CE=2,
∴DE=,
∵CG⊥DE,CD=CE,
∴CG平分DE,
∵∠DCE=90°,
∴DG=CG=DE=,
在Rt△CGB中,CB=6,CG=,
∴BG=,
∴BD=BG-DG=-,
由(2)知BD=2CF,
∴ CF=BD=;
综上所述,满足条件的CF的值为或.
【点睛】本题考查全等三角形的判定与性质,等腰直角三角形的性质,勾股定理,本题属旋转综合题目,通过作辅助线构造全等三角形是解题的关键.
11.(2022·重庆市九年级阶段练习)【问题背景】如图1,P是等边三角形ABC外一点,∠APB=30°,则PA2+PB2=PC2.小明为了证明这个结论,将△PAB绕点A逆时针旋转60°,请根据此思路完成其证明.
【迁移应用】如图2,在等腰直角三角形ABC中,BA=BC,∠ABC=90°,点P在△ABC外部,且∠BPC=45°,若△APC的面积为5.5,求PC.
【答案】(1)【问题背景】见解析;(2)【迁移应用】
【分析】(1)【问题背景】将△PAB绕点A逆时针旋转60°得到△DAC,连接PD,由旋转及等边三角形的性质可得∠PDC=90゜,由勾股定理即可解决;
(2)【迁移应用】过B作BM⊥PB交PC的延长线于点M,连接AM,则易得△PBC≌△MBA,由全等三角形的性质易得∠AMP=90゜,再由面积条件即可求得PC的长.
【详解】(1)【问题背景】将△PAB绕点A逆时针旋转60°得到△DAC,连接PD,如图所示
由旋转的性质得:AD=PA,CD=PB,∠PAD=60゜,∠ADC=∠APB=30゜
∵AD=PA,∠PAD=60゜
∴△PAD是等边三角形
∴PD=PA,∠PDA=60゜
∴∠PDC=∠PDA+∠ADC=60゜+30゜=90゜
在Rt△PDC中,由勾股定理得:
∴
(2)【迁移应用】过B作BM⊥PB交PC的延长线于点M,连接AM,如图所示
则∠PBM=∠ABC=90゜
∴∠PBC+∠CBM=∠CBM+∠MBA
∴∠PBC=∠MBA
∵∠PBM =90゜,∠BPC=45゜
∴∠BMP=∠BPC=45゜
∴PB=MB
在△PBC和△MBA中
∴△PBC≌△MBA(SAS)
∴∠BMA=∠BPC=45゜,PC=AM
∴∠AMP=∠BMP+∠BMA=45゜+45゜=90゜
∵
∴
【点睛】本题考查了旋转的性质,等边三角形的判定与性质,全等三角形的判定与性质,等腰三角形的判定,勾股定理等知识,根据条件作图形的旋转或构造三角形全等是解决问题的关键与难点.
12.(2023·四川达州·八年级统考期末)问题发现:如图,在中,,为边所在直线上的动点(不与点、重合),连结,以为边作,且,根据,得到,结合,得出,发现线段与的数量关系为,位置关系为;
(1)探究证明:如图,在和中,,,且点在边上滑动(点不与点、重合),连接.
①则线段,,之间满足的等量关系式为_____;
②求证: ;
(2)拓展延伸:如图,在四边形中,.若,,求的长.
【答案】(1)①BC =CE+CD;②见解析;(2)AD=6.
【分析】(1)①根据题中示例方法,证明△BAD≌△CAE,得到BD=CE,从而得出BC=CE+CD;
②根据△BAD≌△CAE,得出∠ACE=45°,从而得到∠BCE=90°,则有DE2=CE2+CD2,再根据可得结论;
(2)过点A作AG⊥AD,使AG=AD,连接CG、DG,可证明△BAD≌△CAG,得到CG=BD,在直角△CDG中,根据CD的长求出DG的长,再由DG和AD的关系求出AD.
【详解】解:(1)①如图2,在Rt△ABC中,AB=AC,
∴∠B=∠ACB=45°,
∵∠BAC=∠DAE=90°,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴BD=CE,
∴ BC=BD+CD=CE+CD,
故答案为:BC=BD+CD=CE+CD.
②∵△BAD≌△CAE,
∴∠B=∠ACE=45°,
∵∠ACB=45°,
∴∠BCE=45°+45°=90°,
∴DE2=CE2+CD2,
∵AD=AE,∠DAE=90°,
∴,
∴2AD2=BD2+CD2;
(3)如图3,
过点A作AG⊥AD,使AG=AD,连接CG、DG,
则△DAG是等腰直角三角形,
∴∠ADG=45°,
∵∠ADC=45°,
∴∠GDC=90°,
同理得:△BAD≌△CAG,
∴CG=BD=13,
在Rt△CGD中,∠GDC=90°,
,
∵△DAG是等腰直角三角形,
∴,
∴AD==6.
【点睛】本题是四边形的综合题,考查的是全等三角形的判定和性质、勾股定理,掌握全等三角形的判定定理和性质定理是解题的关键.
13.(2023秋·河南南阳·八年级统考期末)综合与实践:
【问题情景】
综合与实践课上,王老师让同学们以“共顶点的等腰三角形的旋转”为主题开展数学探究活动.
【实践操作】
王老师让同学们先画出两个等边和,将绕点旋转到某一位置,要求同学们观察图形,提出问题并加以解决.
(1)如图①,“慎思组”的同学们连接、,则与有何数量关系?与有何数量关系?请你探究后直接写出结论.
(2)如图②,得知“慎思组”的结论后,“博学组”的同学们又连接,他们认为,如果,且,,就可以求出的长,请写出求解过程.
【类比探究】
(3)如图③,“智慧组”的同学们画出了两个等腰直角三角形和,其中,,;且点恰好落在上,那么、和之间一定存在某种数量关系,请你探究后直接写出它们之间的数量关系.
【答案】(1),
(2),过程见解析
(3)
【分析】(1)通过判定证明全等即可;
(2)由(1)可知边长与角度的关系,然后利用勾股定理求解即可;
(3)与(1)相同,证明全等后,利用勾股定理证明三边关系即可.
【详解】(1)证明:与均为等边三角形
又
在与中
,
(2)证明:由(1)可知 ,,
在等边中,由可得
则,
在中,
,
由勾股定理可得:
(3)连接,
,
在与中
,
【点睛】此题考查旋转模型以及勾股定理,解题关键是找准边与角的关系证明全等,然后利用勾股定理求解.
14.(2023·河南洛阳·八年级校考阶段练习)【问题发现】(1)如图1,和均为等边三角形,点B,D,E在同一直线上,连接,容易发现:①的度数为 ;②线段、之间的数量关系为 ;
【类比探究】
(2)如图2,和均为等腰直角三角形,,点B,D,E在同一直线上,连接,试判断 的度数以及线段、、之间的数量关系,并说明理由;
【问题解决】
(3)如图3,,,,,则的值为 .
【答案】(1)①;②;(2),,见解析;(3)8
【分析】(1)根据等边三角形的性质得到,得到,证明,根据全等三角形的性质证明结论;
(2)由“”可证,可得,即可求解;
(3)如图3,作辅助线构建全等三角形,由“”可证,可得,,可求,根据列方程可得x的值,最后由勾股定理可求解.
【详解】解:(1)∵和均为等边三角形,
∴,
∴,即,
在和中,
,
∴(),
∴,
∴,
故答案为:;
(2),
理由如下:∵,和均为等腰直角三角形,
∴,,
,
即,
在和中,
,
∴(),
∴,
∴,
∵,
∴;
(3)如图3,过点C作,交的延长线于F,过点B作于E,
∴,
∴四边形是矩形,
∴,
∵,
∴,
∵,
∴,
∵,
∴(),
∴,
设,则,,
∴
∴,
∴,,
∴,
∴在中,.
故答案为:.
【点睛】本题是三角形的综合题,考查的是等边三角形的性质,等腰直角三角形的性质,全等三角形的判定和性质,勾股定理等知识,掌握全等三角形的判定定理和性质定理是解题的关键.
15.(2022·福建八年级期中)如图甲,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.解答下列问题
(1)如果AB=AC,∠BAC=90°,①当点D在线段BC上时(与点B不重合),如图乙,线段CF、BD之间的位置关系为 ,数量关系为 .②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?(2)如果AB≠AC,∠BAC≠90°点D在线段BC上运动.试探究:当△ABC满足一个什么条件时,CF⊥BC(点C、F重合除外)?并说明理由.
【答案】(1)①垂直,相等;②成立,理由见解析(2)∠ACB=45°
【分析】(1)①证明△DAB≌△FAC,即可得到CF⊥BD,CF=BD.
②当点D在BC的延长线上时①的结论仍成立.由正方形ADEF的性质可推出△DAB≌△FAC,所以CF=BD,∠ACF=∠ABD.结合∠BAC=90°,AB=AC,得到∠BCF=∠ACB+∠ACF=90度.即CF⊥BD.
(2)当∠ACB=45°时,过点A作AG⊥AC交CB或CB的延长线于点G,则∠GAC=90°,可推出∠ACB=∠AGC,所以AC=AG,由(1)①可知CF⊥BD.
(1)①CF⊥BD,CF=BD
∵∠FAD=∠BAC=90°∴∠BAD=∠CAF 在△BAD与△CAF中,
∵∴△BAD≌△CAF(SAS)
∴CF=BD,∠ACF=∠ABD,
∵∴∠BCF=90°
∴CF⊥BD ;故答案为:垂直,相等;
②成立,理由如下:∵∠FAD=∠BAC=90°∴∠BAD=∠CAF
在△BAD与△CAF中,
∵,∴△BAD≌△CAF(SAS)
∴CF=BD,∠ACF=∠ACB=45°,∴∠BCF=90°,∴CF⊥BD;
(2)当∠ACB=45°时可得CF⊥BC,理由如下:
过点A作AC的垂线与CB所在直线交于G
∵∠ACB=45°∴AG=AC,∠AGC=∠ACG=45°
∵AG=AC,AD=AF,
∵∠GAD=∠GAC﹣∠DAC=90°﹣∠DAC,∠FAC=∠FAD﹣∠DAC=90°﹣∠DAC,
∴∠GAD=∠FAC,∴△GAD≌△CAF(SAS),
∴∠ACF=∠AGD=45°,∴∠GCF=∠GCA+∠ACF=90°,∴CF⊥BC.
【点睛】本题考查三角形全等的判定和直角三角形的判定,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.
15.(2022·福建福州·九年级校考期中)正方形ABCD和正方形AEFG的边长分别为3和1,将正方形AEFG绕点A逆时针旋转.
(1)当旋转至图1位置时,连接BE,DG,则线段BE和DG的关系为 ;
(2)在图1中,连接BD,BF,DF,求在旋转过程中BDF的面积最大值;
(3)在旋转过程中,当点G,E,D在同一直线上时,求线段BE的长.
【答案】(1),;(2)7.5;(3)或
【分析】(1)利用正方形的性质证明即可证得结论;
(2)连接,,,,,设交于点.利用勾股定理求出,,由推出当点F,A,K在同一直线上时,点到的最大距离,由此可得结论;
(3)分两种情形:如图中,当,,共线时,连接交于.如图中,当,,共线时,连接交于.利用勾股定理求出,可得结论.
【详解】解:(1),,理由如下:
如图1中,设交于点,交于点.
四边形、四边形都是正方形,
,,,
,
,
在和中,
,
,
,,
,
,
,
故答案为:BE=DG,BE⊥DG;
(2)如图1中,连接,,,,,设交于点.
四边形、四边形都是正方形,
,,,,
,,
,
,
当点F,A,K在同一直线上时,点到的最大距离,
的面积的最大值为;
(3)如图中,当,,共线时,连接交于.
四边形是正方形,
,,
,
,
,
,
;
如图中,当,,共线时,连接交于.
四边形是正方形,
,,
,
,
,
,;
综上所述,满足条件的的长为或.
【点睛】本题属于四边形综合题,考查了正方形的性质,全等三角形的判定和性质,勾股定理的应用等知识,解题的关键是正确寻找全等三角形解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
全等模型专题3——手拉手模型
全等三角形在中考数学几何模块中占据着重要地位,也是学生必须掌握的一块内容,本专题就全等三角形中的重要模型(手拉手(旋转)模型)进行梳理及对应试题分析,方便掌握。
模型1.手拉手模型(三角形)
【模型解读】
将两个三角形绕着公共顶点(即头)旋转某一角度后能完全重合,则这两个三角形构成手拉手全等,也叫旋转型全等,常用“边角边”判定定理证明全等。
公共顶点A记为“头”,每个三角形另两个顶点逆时针顺序数的第一个顶点记为“左手”,第二个顶点记为“右手”。
对应操作:左手拉左手(即连结BD),右手拉右手(即连结CE),得。
【常见模型及证法】
(等边)
(等腰直角)
(等腰)
例1.如图,点O是等边三角形ABC内的一点,,将△BOC绕点C顺时针旋转60°得△ADC,连接OD.(1)当时, °;(2)当时, °;(3)若,,,则OA的长为 .
例2已知ABC中,∠BAC=60°,以AB和BC为边向外作等边ABD和等边BCE.(1)连接AE、CD,如图1,求证:AE=CD;(2)若N为CD中点,连接AN,如图2,求证:CE=2AN
(3)若AB⊥BC,延长AB交DE于M,DB=,如图3,则BM=_______(直接写出结果)
例3.如图,已知AOB和MON都是等腰直角三角形(OA
例4.在正方形中,点是边上的中点,连接,.
(1)如图1,过点作交的延长线于点,连接,求的面积;
(2)如图2,点是延长线上的一点,连接,过点作,,连接.点是的中点,分别连接,,求证:;
(3)如图3,点是直线上的一动点,连接,过点作,,连接.点是的中点,连接,.当的值最小时,直接写出的面积.
例5.综合与实践:已知是等腰三角形,.
(1)特殊情形:如图1,当∥时,______.(填“>”“<”或“=”);(2)发现结论:若将图1中的绕点顺时针旋转()到图2所示的位置,则(1)中的结论还成立吗?请说明理由.(3)拓展运用:某学习小组在解答问题:“如图3,点是等腰直角三角形内一点,,且,,,求的度数”时,小明发现可以利用旋转的知识,将绕点顺时针旋转90°得到△CAE,连接,构造新图形解决问题.请你根据小明的发现直接写出的度数.
例6.两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,把具有这个规律的图形称为“手拉手”图形.
(1)问题发现:如图1,若和是顶角相等的等腰三角形,BC,DE分别是底边.求证:;
(2)解决问题:如图2,若和均为等腰直角三角形,,点A,D,E在同一条直线上,CM为中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系并说明理由.
图1 图2
模型2.手拉手模型(正多边形型)
【模型解读】将两个多边形绕着公共顶点(即头)旋转某一角度后能完全重合,则这两个多边形构成手拉手全等,也叫旋转型全等,常用“边角边”判定定理证明全等。
【常见模型及证法】
如图,在任意△ABC中,分别以AB、AC为边作正方形ABDE、ACFG,连接EC、BG,则△AEC≌△ABG.
例1.边长为4的正方形ABCD与边长为2的正方形CEFG如图1摆放,将正方形CEFG绕点C顺时针旋转,旋转角为α,连接BG,DE.(1)如图2,求证:△BCG≌△DCE;
(2)如图2,连接DG,BE,判断DG2+BE2否为定值.若是,求这个定值若不是,说明理由;
(3)如图3,当点G恰好落在DE上时,求α的值.
例2.(1)作图发现:如图1,已知,小涵同学以、为边向外作等边和等边,连接,.这时他发现与的数量关系是 .
(2)拓展探究:如图2,已知,小涵同学以、为边向外作正方形和正方形,连接,,试判断与之间的数量关系,并说明理由.
例3.如图,和均为等边三角形,连接BE、CD.
(1)请判断:线段BE与CD的大小关系是 ;
(2)观察图,当和分别绕点A旋转时,BE、CD之间的大小关系是否会改变
(3)观察如图和4,若四边形ABCD、DEFG都是正方形,猜想类似的结论是________,在如图中证明你的猜想.
(4)这些结论可否推广到任意正多边形(不必证明),如图,BB1与EE1的关系是 ;它们分别在哪两个全等三角形中 ;请在如图中标出较小的正六边形AB1C1D1E1F1的另五个顶点,连接图中哪两个顶点,能构造出两个全等三角形?
例4.如图1,图2,图3,在中,分别以为边,向外作正三角形,正四边形,正五边形,相交于点.(正多边形的各边相等,各个内角也相等)
①如图1,求证:△ABE≌△ADC;②探究:如图1,∠BOD= ;
③如图2,∠BOD= ;④如图3,∠BOD= .
课后专项训练
1.如图,在△ABC中以AC,BC为边向外作正方形ACFG与正方形BCDE,连结DF,并过C点作CH⊥AB于H并交FD于M.若∠ACB=120°,AC=3,BC=2,则MD的长为( )
A. B. C. D.
第1题图 第2题图
2.如图,在中,,D是边上的一个动点,连接,并将线段绕点A逆时针旋转后得线段,连接,在点D运动过程中,线段长度的最小值是_________.
3.已知:如图,在△ABC中,AB=AC,在△ADE中,AD=AE,且∠BAC=∠DAE,连接BD,CE交于点F,连接AF.(1)求证:△ABD≌△ACE;(2)求证:FA平分∠BFE.
4.△ABC中,,,点在边上,将线段逆时针旋转得到,连接.
(1)当,时,求证:.(2)当,时,若,求的值.
5.已知:在△ABC中,CA=CB,∠ACB=90 ,D为△ABC外一点,且满足∠ADB=90°.(1)如图1,若,AD=1,求DB的长.(2)如图1,求证:.
(3)如图2所示,过C作CE⊥AD于E,BD=2,AD=6,求CE的长.
6.(1)如图1,在中,,,,则与的数量关系是 ,与延长线的夹角 ;(2)如图2,四边形中,,,,连接,猜想、、之间的数量关系,并证明你的猜想;(3)如图3,四边形中,,,,,,请直接写出的长为 .
7.如图,D为内一点,,,将绕着点A顺时针旋转能与线段重合.
(1)求证:;(2)若,求的度数.
8.两个顶角相等的等腰三角形,如果具有公共的顶角顶点,并将它们的底角顶点分别对应连接起来得到两个全等三角形,我们把这样的图形称为“手拉手”图形.如图1,在“手拉手”图形中,AB=AC,AD=AE,∠BAC=∠DAE,连接BD,CE,则△ABD≌△ACE.
(1)请证明图1的结论成立;(2)如图2,△ABC和△AED是等边三角形,连接BD,EC交于点O,求∠BOC的度数;(3)如图3,AB=BC,∠ABC=∠BDC=60°,试探究∠A与∠C的数量关系.
9.如图1,在Rt△ABC中,∠B=90°,AB=BC=4,点D,E分别为边AB,BC上的中点,且BD=BE=.
(1)如图2,将△BDE绕点B逆时针旋转任意角度α,连接AD,EC,则线段EC与AD的关系是 ;
(2)如图3,DE∥BC,连接AE,判断△EAC的形状,并求出EC的长;
(3)继续旋转△BDE,当∠AEC=90°时,请直接写出EC的长.
10.(1)如图1,在中,,,点D,E分别在边CA,CB上,且,连接AE,BD,F为AE的中点,连接CF交BD于点G,则线段CF所在直线与线段BD所在直线的位置关系是_______,线段CF和线段BD的数量关系为______.(2)将绕点C逆时针旋转至图2所示位置时,(1)中的结论是否仍然成立 若成立,请给出证明;若不成立,请说明理由.
(3)将绕点C逆时针在平面内旋转,在旋转过程中,当B,D,E三点在同一条直线上时,CF的长为________.
11.【问题背景】如图1,P是等边三角形ABC外一点,∠APB=30°,则PA2+PB2=PC2.小明为了证明这个结论,将△PAB绕点A逆时针旋转60°,请根据此思路完成其证明.
【迁移应用】如图2,在等腰直角三角形ABC中,BA=BC,∠ABC=90°,点P在△ABC外部,且∠BPC=45°,若△APC的面积为5.5,求PC.
12.问题发现:如图,在中,,为边所在直线上的动点(不与点、重合),连结,以为边作,且,根据,得到,结合,得出,发现线段与的数量关系为,位置关系为;
(1)探究证明:如图,在和中,,,且点在边上滑动(点不与点、重合),连接.①则线段,,之间满足的等量关系式为____ ;②求证: ;(2)拓展延伸:如图,在四边形中,.若,,求的长.
13.综合与实践:
【问题情景】综合与实践课上,王老师让同学们以“共顶点的等腰三角形的旋转”为主题开展数学探究活动.
【实践操作】王老师让同学们先画出两个等边和,将绕点旋转到某一位置,要求同学们观察图形,提出问题并加以解决.
(1)如图①,“慎思组”的同学们连接、,则与有何数量关系?与有何数量关系?请你探究后直接写出结论.
(2)如图②,得知“慎思组”的结论后,“博学组”的同学们又连接,他们认为,如果,且,,就可以求出的长,请写出求解过程.
【类比探究】(3)如图③,“智慧组”的同学们画出了两个等腰直角三角形和,其中,,;且点恰好落在上,那么、和之间一定存在某种数量关系,请你探究后直接写出它们之间的数量关系.
14.【问题发现】(1)如图1,△ABC和△ADE均为等边三角形,点B,D,E在同一直线上,连接,容易发现:①的度数为 ;②线段、之间的数量关系为 ;
【类比探究】(2)如图2,△ABC和△ADE均为等腰直角三角形,,点B,D,E在同一直线上,连接,试判断 的度数以及线段、、之间的数量关系,并说明理由;
【问题解决】(3)如图3,,,,,则的值为 .
15.如图甲,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.解答下列问题
(1)如果AB=AC,∠BAC=90°,①当点D在线段BC上时(与点B不重合),如图乙,线段CF、BD之间的位置关系为 ,数量关系为 .②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?(2)如果AB≠AC,∠BAC≠90°点D在线段BC上运动.试探究:当△ABC满足一个什么条件时,CF⊥BC(点C、F重合除外)?并说明理由.
16.正方形ABCD和正方形AEFG的边长分别为3和1,将正方形AEFG绕点A逆时针旋转.
(1)当旋转至图1位置时,连接BE,DG,则线段BE和DG的关系为 ;
(2)在图1中,连接BD,BF,DF,求在旋转过程中BDF的面积最大值;
(3)在旋转过程中,当点G,E,D在同一直线上时,求线段BE的长.
八年级全等模型专题3—— 手拉手模型
全等三角形在中考数学几何模块中占据着重要地位,也是学生必须掌握的一块内容,本专题就全等三角形中的重要模型(手拉手(旋转)模型)进行梳理及对应试题分析,方便掌握。
模型1.手拉手模型(三角形)
【模型解读】
将两个三角形绕着公共顶点(即头)旋转某一角度后能完全重合,则这两个三角形构成手拉手全等,也叫旋转型全等,常用“边角边”判定定理证明全等。
公共顶点A记为“头”,每个三角形另两个顶点逆时针顺序数的第一个顶点记为“左手”,第二个顶点记为“右手”。
对应操作:左手拉左手(即连结BD),右手拉右手(即连结CE),得。
【常见模型及证法】
(等边)
(等腰直角)
(等腰)
例1.(2022秋·吉林松原·九年级统考期中)如图,点O是等边三角形ABC内的一点,,将△BOC绕点C顺时针旋转60°得△ADC,连接OD.(1)当时, °;(2)当时, °;(3)若,,,则OA的长为 .
【答案】(1)40; (2)60;(3)
【分析】(1)证明△COD是等边三角形,得到∠ODC=60°,即可得到答案;
(2)利用∠ADC-∠ODC求出答案;(3)由△BOC≌△ADC,推出∠ADC=∠BOC=150°,AD=OB=8,根据△COD是等边三角形,得到∠ODC=60°,OD=,证得△AOD是直角三角形,利用勾股定理求出.
【详解】(1)解:∵CO=CD,∠OCD=60°,∴△COD是等边三角形;∴∠ODC=60°,
∵∠ADC=∠BOC=,∴∠ADC-∠ODC=40°,故答案为:40;
(2)∵∠ADC=∠BOC=,∴∠ADC-∠ODC=60°,故答案为:60;
(3)解:当,即∠BOC=150°,∴△AOD是直角三角形.
∵△BOC≌△ADC,∴∠ADC=∠BOC=150°,AD=OB=8,
又∵△COD是等边三角形,∴∠ODC=60°,OD=,∴∠ADO=90°,
即△AOD是直角三角形,∴,故答案为:.
【点睛】本题以“空间与图形”中的核心知识(如等边三角形的性质、全等三角形的性质与证明、直角三角形的判定、多边形内角和等)为载体,内容由浅入深,层层递进.试题中几何演绎推理的难度适宜,蕴含着丰富的思想方法(如运动变化、数形结合、分类讨论、方程思想等),能较好地考查学生的推理、探究及解决问题的能力.
例2.(2022·湖北武汉·八年级期末)已知ABC中,∠BAC=60°,以AB和BC为边向外作等边ABD和等边BCE.(1)连接AE、CD,如图1,求证:AE=CD;(2)若N为CD中点,连接AN,如图2,求证:CE=2AN
(3)若AB⊥BC,延长AB交DE于M,DB=,如图3,则BM=_______(直接写出结果)
【答案】(1)见解析(2)见解析(3)
【分析】(1)先判断出∠DBC=∠ABE,进而判断出△DBC≌△ABE,即可得出结论;
(2)先判断出△ADN≌△FCN,得出CF=AD,∠NCF=∠AND,进而判断出∠BAC=∠ACF,即可判断出△ABC≌△CFA,即可得出结论;(3)先判断出△ABC≌△HEB(ASA),得出,,再判断出△ADM≌△HEM (AAS),得出AM=HM,即可得出结论.
(1)解:∵△ABD和△BCE是等边三角形,∴BD=AB,BC=BE,∠ABD=∠CBE=60°,
∴∠ABD+∠ABC=∠CBE+∠ABC,∴∠DBC=∠ABE,∴△ABE≌△DBC(SAS),∴AE=CD;
(2)解:如图,延长AN使NF=AN,连接FC,
∵N为CD中点,∴DN=CN,
∵∠AND=∠FNC,∴△ADN≌△FCN(SAS),∴CF=AD,∠NCF=∠AND,
∵∠DAB=∠BAC=60°∴∠ACD +∠ADN=60°
∴∠ACF=∠ACD+∠NCF=60°,∴∠BAC=∠ACF,
∵△ABD是等边三角形,∴AB=AD,∴AB=CF,
∵AC=CA,∴△ABC≌△CFA (SAS),∴BC=AF,
∵△BCE是等边三角形,∴CE=BC=AF=2AN;
(3)解: ∵△ABD是等边三角形,∴,∠BAD=60°,
在Rt△ABC中,∠ACB=90°-∠BAC=30°,∴,
如图,过点E作EH // AD交AM的延长线于H,
∴∠H=∠BAD=60°,∵△BCE是等边三角形,∴BC=BE,∠CBE=60°,
∵∠ABC=90°,∴∠EBH=90°-∠CBE=30°=∠ACB,
∴∠BEH=180°-∠EBH-∠H=90°=∠ABC,
∴△ABC≌△HEB (ASA),∴,,∴AD=EH,
∵∠AMD=∠HME,∴△ADM≌△HEM (AAS),∴AM=HM,
∴
∵,,∴.故答案为:.
【点睛】此题是三角形综合题,主要考查了等边三角形的性质,含30°角的直角三角形的性质,全等三角形的判定和性质,构造出全等三角形是解本题的关键.
例3.(2022·湖北·襄阳市九年级阶段练习)如图,已知AOB和MON都是等腰直角三角形(OA
【答案】(1)见解析;(2)①见解析;②或.
【分析】(1)利用SAS定理证明即可;
(2)①连接,证明,即可证;②当点N在线段上时,连接,在中构造勾股定理的等量关系;当点M在线段上时,同理即可求得.
(1)证明:,,即.
和是等腰直角三角形,,(SAS) .
(2)解:①证明:如图,连接.
,,即.
和是等腰直角三角形,,
,,.
是等腰直角三角形,,.
②或.∵△AOB和△MON都是等腰直角三角形,OB=4,ON =3,∴.
当点N在线段上时,如图,连接,设,
由(1)可知.∴,.
∴,
∴,∴是直角三角形,.
又∵,∴,
解得:(舍去)∴;
当点M在线段上时,如图,连接,设,由(2)①可知.
∴,.
∴,
∴,∴是直角三角形,.
又∵,∴,
解得: (舍去)∴
综上所述:的长为或.
【点睛】本题主要考查全等三角形的判定与性质、等腰直角三角形的性质,三点共线分类讨论,对几何题目的综合把握是解题关键.
例4.(2023春·重庆巴南·八年级统考期末)在正方形中,点是边上的中点,连接,.
(1)如图1,过点作交的延长线于点,连接,求的面积;
(2)如图2,点是延长线上的一点,连接,过点作,,连接.点是的中点,分别连接,,求证:;
(3)如图3,点是直线上的一动点,连接,过点作,,连接.点是的中点,连接,.当的值最小时,直接写出的面积.
【答案】(1)(2)证明见解析(3)
【分析】(1)利用证明得,从而求出,由此即可求出的面积.(2)过点作交于点,连接,利用一线三直角模型可得(),从而可得:,再证明可得为等腰直角三角形,,进而得出结论;(3)由已知可得:是等腰直角三角形,进而可得,,即当E点在AM上时,最小,再由三角形全都转换线段关系得到,由勾股定理求出即可解题.
【详解】(1)解:∵;∴;
∵四边形是正方形;∴,;
∵点是的中点,;∴;
∵;
∴;∴;∴;
∴;
(2)证明:如解(2)图,过点作交于点,连接.
∵;∴∴;
∵;∴;∴,;
∵点是的中点,;∴,:
∴;∴;∴,;
∴;∴;∴;
(3)解:∵,,∴是等腰直角三角形,,
又∵点是的中点,∴,∴,
∴当E点在上时,最小,如解(3)图,过点作交的延长线于点,
同理(1)可得:;∴;,,
∴,
又∵∴,
又∵,∴,∴,
∴,
在中,,,
∴,解得:,∴
【点睛】本题主要考查了正方形的性质与判定,勾股定理,全等三角形的性质与判定,解题(3)的关键在于能够证明.
例5.(2022·山西大同·九年级期中)综合与实践:已知是等腰三角形,.
(1)特殊情形:如图1,当∥时,______.(填“>”“<”或“=”);(2)发现结论:若将图1中的绕点顺时针旋转()到图2所示的位置,则(1)中的结论还成立吗?请说明理由.(3)拓展运用:某学习小组在解答问题:“如图3,点是等腰直角三角形内一点,,且,,,求的度数”时,小明发现可以利用旋转的知识,将绕点顺时针旋转90°得到,连接,构造新图形解决问题.请你根据小明的发现直接写出的度数.
【答案】(1)=;(2)成立,理由见解析;(3)∠BPA=135°.
【分析】(1)由DE∥BC,得到∠ADE=∠B,∠AED=∠C,结合AB=AC,得到DB=EC;
(2)由旋转得到的结论判断出△DAB≌△EAC,得到DB=CE;(3)由旋转构造出△APB≌△AEC,再用勾股定理计算出PE,然后用勾股定理逆定理判断出△PEC是直角三角形,在简单计算即可.
【详解】解:(1)∵DE∥BC,∴∠ADE=∠B,∠AED=∠C,
∵AB=AC,∴∠B=∠C,∴∠ADE=∠AED,∴AD=AE,∴DB=EC,故答案为:=;
(2)成立.证明:由①易知AD=AE,∴由旋转性质可知∠DAB=∠EAC,
在△DAB和△EAC中,∴△DAB≌△EAC(SAS),∴DB=CE;
(3)如图,
将△APB绕点A旋转90°得△AEC,连接PE,∴△APB≌△AEC,
∴AE=AP=2,EC=BP=1,∠PAE=90°,∴∠AEP=∠APE=45°,
在Rt△PAE中,由勾股定理可得,PE=2,
在△PEC中,PE2=(2)2=8,CE2=12=1,PC2=32=9,
∵PE2+CE2=PA2,∴△PEC是直角三角形,∴∠PEC=90°,∴∠AEC=135°,
又∵△APB≌△AEC,∴∠BPA=∠CEA=135°.
【点睛】本题主要考查了旋转的性质,平行线的性质,全等三角形的性质和判定,勾股定理及其逆定理,解本题的关键是构造全等三角形,也是本题的难点.
例6.(2022·青海·中考真题)两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,把具有这个规律的图形称为“手拉手”图形.
(1)问题发现:如图1,若和是顶角相等的等腰三角形,BC,DE分别是底边.求证:;
(2)解决问题:如图2,若和均为等腰直角三角形,,点A,D,E在同一条直线上,CM为中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系并说明理由.
图1 图2
【答案】(1)见解析 (2);
【分析】(1)先判断出∠BAD=∠CAE,进而利用SAS判断出△BAD≌△CAE,即可得出结论;
(2)同(1)的方法判断出△BAD≌△CAE,得出AD=BE,∠ADC=∠BEC,最后用角的差,即可得出结论.
【解析】(1)证明:∵和是顶角相等的等腰三角形,
∴,,,
∴,∴.
在和中,,∴,∴.
(2)解:,,
理由如下:由(1)的方法得,,∴,,
∵是等腰直角三角形,∴,
∴,∴,
∴.
∵,,∴.∵,∴,
∴.∴.
【点睛】此题是三角形综合题,主要考查了全等三角形的判定和性质,等腰三角形,等边三角形,等腰直角三角形的性质,判断出△ACD≌△BCE是解本题的关键.
模型2.手拉手模型(正多边形型)
【模型解读】将两个多边形绕着公共顶点(即头)旋转某一角度后能完全重合,则这两个多边形构成手拉手全等,也叫旋转型全等,常用“边角边”判定定理证明全等。
【常见模型及证法】
如图,在任意△ABC中,分别以AB、AC为边作正方形ABDE、ACFG,连接EC、BG,则△AEC≌△ABG.
例1.(2023春·浙江·八年级专题练习)边长为4的正方形ABCD与边长为2的正方形CEFG如图1摆放,将正方形CEFG绕点C顺时针旋转,旋转角为α,连接BG,DE.
(1)如图2,求证:△BCG≌△DCE;
(2)如图2,连接DG,BE,判断DG2+BE2否为定值.若是,求这个定值若不是,说明理由;
(3)如图3,当点G恰好落在DE上时,求α的值.
【答案】(1)见解析;(2)48;(3)
【分析】(1)通过边角边判定三角形全等;(2)连接,设交于点,交于点,先证明,由勾股定理可得;(3)作于点,则,且,由含30度角的直角三角形的性质求解.
【详解】(1)四边形与为正方形,,,
,,,
在和中, (SAS),
(2)连接,设交于点,交于点,
,,,
在△和中,,
,,
,
由勾股定理得,,
,
,,,,
(3)作于点,如图,
△为等腰直角三角形,,且,
在中,,,,
..
【点睛】本题考查四边形与三角形的综合问题,解题关键是熟练掌握正方形与直角三角形的性质,通过添加辅助线求解.
例2.(2023·河南鹤壁市八年级月考)(1)作图发现:如图1,已知,小涵同学以、为边向外作等边和等边,连接,.这时他发现与的数量关系是 .
(2)拓展探究:如图2,已知,小涵同学以、为边向外作正方形和正方形,连接,,试判断与之间的数量关系,并说明理由.
【答案】(1)BE=CD;(2)BE=CD,理由见解析;
【分析】(1)利用等边三角形的性质得出,然后有,再利用SAS即可证明,则有;
(2)利用正方形的性质得出,然后有,再利用SAS即可证明,则有;
【详解】(1)如图1所示:
和都是等边三角形,,
,即,
在和中,,.
(2),四边形和均为正方形,
,,,
,
在和中,,,
例3.(2023·福建福州市·九年级月考)如图,和均为等边三角形,连接BE、CD.
(1)请判断:线段BE与CD的大小关系是 ;
(2)观察图,当和分别绕点A旋转时,BE、CD之间的大小关系是否会改变
(3)观察如图和4,若四边形ABCD、DEFG都是正方形,猜想类似的结论是________,在如图中证明你的猜想.
(4)这些结论可否推广到任意正多边形(不必证明),如图,BB1与EE1的关系是 ;它们分别在哪两个全等三角形中 ;请在如图中标出较小的正六边形AB1C1D1E1F1的另五个顶点,连接图中哪两个顶点,能构造出两个全等三角形?
【答案】(1) BE=CD (2)线段BE与CD的大小关系不会改变 (3)AE=CG,证明见解析 (4)这些结论可以推广到任意正多边形.如图5,BB1=EE1,它们分别在△AE1E和△AB1B中,如图6,连接FF1,可证△AB1B≌△AF1F.图形见解析.
【分析】本题是变式拓展题,图形由简单到复杂,需要从简单图形中探讨解题方法,并借鉴用到复杂图形中;证明三角形全等时,用旋转变换寻找三角形全等的条件.
【详解】(1)线段BE与CD的大小关系是BE=CD;(2)线段BE与CD的大小关系不会改变;
(3)AE=CG.证明:如图4,正方形ABCD与正方形DEFG中,∵AD=CD,DE=DG,∠ADC=∠GDE=90°,
又∠CDG=90°+∠ADG=∠ADE,∴△ADE≌△CDG,∴AE=CG.
(4)这些结论可以推广到任意正多边形.
如图5,BB1=EE1,它们分别在△AE1E和△AB1B中,如图6,连接FF1,可证△AB1B≌△AF1F.
【点睛】本题综合考查全等三角形、等边三角形和多边形有关知识.注意对三角形全等的证明方法的发散.
例4.(2023·江苏无锡·八年级校考阶段练习)如图1,图2,图3,在中,分别以为边,向外作正三角形,正四边形,正五边形,相交于点.(正多边形的各边相等,各个内角也相等)
①如图1,求证:△ABE≌△ADC;②探究:如图1,∠BOD= ;
③如图2,∠BOD= ;④如图3,∠BOD= .
【答案】①见解析;②60°;③90°;④108°
【分析】①根据等边三角形的性质可以得出△ABE≌△ADC.
②③④根据△ABE≌△ADC可得∠CDA=∠EBA,根据三角形内角和可得∠BOD=∠BAD,从而求解.
【详解】解:①证明:如图,
∵△ABD和△AEC是等边三角,∴AD=AB,AE=AC,∠DAB=∠EAC=∠ABD=∠ADB=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,即∠DAC=∠BAE.
在△ABE和△ADC中,,∴△ABE≌△ADC(SAS);
②,,∵∠AFD=∠OFB,∴∠BOD=∠BAD=60°;
③如图, 四边形和四边形是正方形,
,,,,
,即,
在和中,,,,
∵∠AHB=∠OHD,∴∠BOD=∠BAD=90°;
④如图,五边形和五边形是正五边形,
,,,
,,,
在和中,,,,
∵∠AMB=∠OMD,∴∠BOD=∠BAD=(5-2)×180°÷5=108°.
【点睛】本题考查了等边三角形的性质的运用,正方形的性质的运用,正五边形的性质的运用及正边形的性质的运用,全等三角形的判定及性质的运用,解答时根据正多边形的性质证明三角形全等是关键.
课后专项训练
1.(2022·浙江·温州一模)如图,在△ABC中以AC,BC为边向外作正方形ACFG与正方形BCDE,连结DF,并过C点作CH⊥AB于H并交FD于M.若∠ACB=120°,AC=3,BC=2,则MD的长为( )
A. B. C. D.
【答案】A
【分析】过D作DN⊥CF于点N,作DP⊥HM于点P,过点F作FQ⊥HM,交HM的延长线于点Q,依据勾股定理即可求得DF的长,再根据全等三角形的对应边相等得到FQ=DP,进而证明
△FQM≌△DPM,得到M是FD的中点,由此可得DM=DF.
【详解】如图所示,过D作DN⊥CF于点N,作DP⊥HM于点P,过点F作FQ⊥HM,交HM的延长线于点Q,
∵∠ACB=120°,∠ACF=∠BCD=90°,∴∠DCN=60°,∠CDN=30°,
又∵BC=DC=2,AC=FC=3,
∴CNCD=1,FN=CF﹣CN=3﹣1=2,DN,
Rt△DFN中,DF.
∵四边形BCDE是正方形,∴BC=CD,∠BCD=90°,
又∵CH⊥AB,∴∠DCP+∠BCH=∠CBH+∠BCH=90°,∴∠DCP=∠CBH,
又∵∠DPC=∠BHC=90°,∴△DCP≌△CBH(AAS),
∴DP=CH,同理可得△ACH≌△CFQ,∴FQ=CH,∴FQ=DP,
又∵∠Q=∠DPM=90°,∠FMQ=∠DMP,∴△FQM≌△DPM(AAS),
∴FM=DM,即M是FD的中点,
∴DMDF.故选:A
【点睛】本题考查了正方形的性质,全等三角形的判定与性质以及勾股定理的综合运用,通过作辅助线构造全等三角形,灵活运用全等三角形的对应边相等是解题的关键.
2.(2022·广东茂名·二模)如图,在中,,D是边上的一个动点,连接,并将线段绕点A逆时针旋转后得线段,连接,在点D运动过程中,线段长度的最小值是_________.
【答案】
【分析】过点作于点,在上取点,使,连接,先根据直角三角形的性质、勾股定理可得,根据等腰直角三角形的判定与性质可得,从而可得,再根据旋转的性质可得,然后根据三角形全等的判定证出,根据全等三角形的性质可得,最后根据垂线段最短可得当时,的长度最小,在中,解直角三角形即可得.
【详解】解:如图,过点作于点,在上取点,使,连接,
,,
,是等腰直角三角形,
,,
,
由旋转的性质得:,,
,,,
在和中,,,,
如图,由垂线段最短可知,当时,的长度最小,
在中,,
即线段长度的最小值是,故答案为:.
【点睛】本题考查了含角的直角三角形的性质、勾股定理、三角形全等的判定定理与性质、旋转的性质、解直角三角形等知识点,通过作辅助线,构造全等三角形是解题关键.
3.(2022·安徽芜湖·八年级期末)已知:如图,在△ABC中,AB=AC,在△ADE中,AD=AE,且∠BAC=∠DAE,连接BD,CE交于点F,连接AF.(1)求证:△ABD≌△ACE;(2)求证:FA平分∠BFE.
【答案】(1)见解析(2)见解析
【分析】(1)根据SAS证明结论即可;(2)作AM⊥BD于M,作AN⊥CE于N.由(1)可得BD=CE,S△BAD=S△CAE,然后根据角平分线的性质即可解决问题.
【解析】(1)证明:∵∠BAC=∠DAE,
∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,
在△BAD和△CAE中,,∴△BAD≌△CAE(SAS);
(2)证明:如图,作AM⊥BD于M,作AN⊥CE于N.
由△BAD≌△CAE,∴BD=CE,S△BAD=S△CAE,
∵,∴AM=AN,
∴点A在∠BFE平分线上,∴FA平分∠BFE.
【点睛】本题考查全等三角形的判定和性质、三角形的面积,解题的关键是熟练掌握全等三角形的判定和性质,学会转化的思想,巧用等积法进行证明.
4.(2023春·八年级单元测试)中,,,点在边上,将线段逆时针旋转得到,连接.
(1)当,时,求证:.(2)当,时,若,求的值.
【答案】(1)证明见解析(2)
【分析】(1)根据题意证明,得出,,,勾股定理即可得证;(2)在的延长线上取点,使,由同理得,设,根据勾股定理得出,作于,得出是等腰直角三角形,分别求得,即可求解.
【详解】(1)证明:如图,连接,
,,
在和中,,
,,,
,,
,;
(2)在的延长线上取点,使
,由同理得,,
,设,∴
作于,,是等腰直角三角形,
∴.
【点睛】本题考查了旋转的性质,勾股定理,含30度角的直角三角形的性质,等腰直角三角形的性质,全等三角形的性质与判定,掌握旋转的性质是解题的关键.
5.(2022·福建·长汀县第四中学八年级阶段练习)已知:在△ABC中,CA=CB,∠ACB=90 ,D为△ABC外一点,且满足∠ADB=90°.
(1)如图1,若,AD=1,求DB的长.(2)如图1,求证:.
(3)如图2所示,过C作CE⊥AD于E,BD=2,AD=6,求CE的长.
【答案】(1);(2)见解析;(3)2
【分析】(1)在Rt△ABC中,根据勾股定理,得AB=2,在Rt△ABD中,根据勾股定理,得;
(2)过C点作CF⊥CD,构造手拉手模型,运用等腰直角三角形的性质可得证;
(3)过C点作CF⊥CD,构造手拉手模型,运用三角形全等可得证.
【详解】(1)解:在Rt△ABC中,∵,∴,
∴在Rt△ABD中,.
(2)证明:如图,过C点作CF⊥CD交DB的延长线于点F.
∵∠ACB=∠DCF=90°,∴∠ACD=∠BCF,
∵∠CAD+∠CBD=360°-(∠ACB+∠ADB)=180°,∠CBF+∠CBD=180°,
∴∠CAD=∠CBF,又∵CA=CB,∴△CAD≌△CBF(ASA),
∴CD=CF,AD=BF,∴,
∵DF=DB+BF=DB+DA,∴.
(3)解:如图,过C点作CF⊥CD交AD与F点,
∵∠ACB=∠DCF=90°,即∠ACF+∠BCF=∠BCD+∠BCF=90°,∴∠ACF=∠BCD,
∵∠AFC=∠FCD+∠CDA=90°+∠CDA,∠CDB=∠CDA+∠ADB=90°+∠CDA,∴∠AFC=∠CDB,
又∵CA=CB,∴△CAF≌△CBD(AAS), ∴CF=CD,AF=BD,
∴△CDF是等腰直角三角形,
又∵CE⊥AD,∴E为DF中点,
∵AD=6,AF=BD=2,∴FD=AD-AF=4,
∴.
【点睛】本题考查了勾股定理,等腰直角三角形的性质,等腰三角形的性质,三角形的全等,手拉手模型的构造,熟练构造手拉手模型是解题的关键.
6.(2023春·湖北武汉·八年级校考阶段练习)
(1)如图1,在中,,,,则与的数量关系是 ,与延长线的夹角 ;(2)如图2,四边形中,,,,连接,猜想、、之间的数量关系,并证明你的猜想;(3)如图3,四边形中,,,,,,请直接写出的长为 .
【答案】(1),(2)(3)
【分析】(1)证明≌即可.
(2)由(1)的证明方法可知:将绕点顺时针旋转, 连接、,证明≌,再为直角三角形,用勾股定理即可.
(3)由(1)的证明方法可知:将绕点顺时针旋转, 连接、,延长交于,再证明,用勾股定理即可求解.
【详解】(1)与的数量关系:,
证明:,
,,
在和中,
≌,,
故与的数量关系:;,
≌,,即:,
在中:
.故.
(2)
结论:,
证明:如图,将绕点顺时针旋转,连接、,
,,是等边三角形,,
, ,,
在和中,
≌,,,
,,
,
,
在中,.
(3)
解:如图,将绕点顺时针旋转,连接、,延长交于,
,,是等腰直角三角形,
,,,
,,
,,
在和中,
≌,
,,
,
,,
设,,则有,,
在中,,
在中,,
由①②解得,,
在中,故的长为.
【点睛】本题考查了三角形全等及性质、勾股定理在旋转中典型模型“手拉手”的综合应用,掌握典型模型的解决方法是解题的关键.
7.(2023春·广东汕头·九年级校考开学考试)如图,D为内一点,,,将绕着点A顺时针旋转能与线段重合.
(1)求证:;(2)若,求的度数.
【答案】(1)见解析(2)
【分析】(1)根据将绕着点A顺时针旋转能与线段重合,得,,通过证明,即可证出;
(2)由得:,再根据,,得,即可求出答案.
【详解】(1)证明:∵将绕着点A顺时针旋转能与线段重合,
∴,,
∵,
∴,
∴,
在和中,
,
∴,
∴;
(2)解:由得:,
∵,
∴,
∵,,
∴,
∴.
【点睛】本题主要考查了旋转的性质、等腰三角形是性质、三角形全等的判定与性质等知识,证明出是解题的关键.
8.(2023春·全国·七年级专题练习)两个顶角相等的等腰三角形,如果具有公共的顶角顶点,并将它们的底角顶点分别对应连接起来得到两个全等三角形,我们把这样的图形称为“手拉手”图形.如图1,在“手拉手”图形中,AB=AC,AD=AE,∠BAC=∠DAE,连接BD,CE,则△ABD≌△ACE.
(1)请证明图1的结论成立;
(2)如图2,△ABC和△AED是等边三角形,连接BD,EC交于点O,求∠BOC的度数;
(3)如图3,AB=BC,∠ABC=∠BDC=60°,试探究∠A与∠C的数量关系.
【答案】(1)见解析(2)60°(3)∠A+∠BCD=180°,理由见解析
【分析】(1)利用等式的性质得出∠BAD=∠CAE,即可得出结论;
(2)同(1)的方法判断出△ABD≌△ACE,得出∠ADB=∠AEC,再利用对顶角和三角形的内角和定理判断出∠BOC=60°,即可得出答案;(3)先判断出△BDP是等边三角形,得出BD=BP,∠DBP=60°,进而判断出△ABD≌△CBP(SAS),即可得出结论.
【详解】(1)解:证明:∵∠BAC=∠DAE,
∴∠BAC+∠CAD=∠DAE+∠CAD,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS);
(2)如图2,
∵△ABC和△ADE是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴∠ADB=∠AEC,
令AD与CE交于点G,
∵∠AGE=∠DGO,
∴180°-∠ADB-∠DGO=180°-∠AEC-∠AGE,
∴∠DOE=∠DAE=60°,
∴∠BOC=60°;
(3)∠A+∠BCD=180°.理由:
如图3,延长DC至P,使DP=DB,
∵∠BDC=60°,
∴△BDP是等边三角形,
∴BD=BP,∠DBP=60°,
∵∠ABC=60°=∠DBP,
∴∠ABD=∠CBP,
∵AB=CB,
∴△ABD≌△CBP(SAS),
∴∠BCP=∠A,
∵∠BCD+∠BCP=180°,
∴∠A+∠BCD=180°.
【点睛】此题是三角形综合题,主要考查了等腰三角形的性质,等边三角形的性质,全等三角形的判定和性质,构造等边三角形是解本题的关键.
9.(2022春·湖南长沙·八年级长沙市湘郡培粹实验中学校考阶段练习)如图1,在Rt△ABC中,∠B=90°,AB=BC=4,点D,E分别为边AB,BC上的中点,且BD=BE=.
(1)如图2,将△BDE绕点B逆时针旋转任意角度α,连接AD,EC,则线段EC与AD的关系是 ;
(2)如图3,DE∥BC,连接AE,判断△EAC的形状,并求出EC的长;
(3)继续旋转△BDE,当∠AEC=90°时,请直接写出EC的长.
【答案】(1)EC=AD,EC⊥AD(2)等腰三角形,(3)
【分析】(1)延长CE交AD于F,交AB于O,证明△ABD≌△CBE(SAS),得∠BCE=∠BAD,CE=AD,再由∠AOF=∠BOC,可得∠AFC=∠ABC=90°,即可得到结论;(2)设DE与AB的交点为H,可得AB是DE的垂直平分线,利用勾股定理可求出AE的长,由(1)知CE=AD,从而得出答案;(3)分当点E在BC上方时和当点E在BC下方时,分别画图,利用勾股定理计算即可.
(1)EC与AD垂直且相等,理由如下:
延长CE交AD于F,交AB于O,
∵△BDE和△ABC都是等腰直角三角形,
∴BD=BE,AB=BC,∠DBE=∠ABC=90°,
∴∠ABD=∠CBE,
∴△ABD≌△CBE(SAS),
∴∠BCE=∠BAD,CE=AD,
∵∠AOF=∠BOC,
∴∠AFE=∠ABC=90°,
∴AD⊥CE,
∴故答案为:EC=AD,EC⊥AD;
(2)设DE与AB的交点为H,
∵DE∥BC,
∴∠AHE=∠ABC=90°,
∵BD=BE,
∴AB是DE的垂直平分线,
∴AD=AE,
由(1)知AD=CE,
∴AE=CE,
∴△ACE是等腰三角形,
∵BE=,
∴BH=HE=1,
∴AH=AB﹣BH=4﹣1=3,
在Rt△AHE中,由勾股定理得:AE=,
∴CE=AE=;
(3)
如图4,当点E在BC上方时,
过点B作BG⊥DE于G,
∵∠AEC=90°,CE⊥AD,
∴A、E、D三点共线,
∴AG=,
∴AD=AG+DG=,
∴CE=AD=+1;
如图,当点E在BC下方时,
同理可得CE=CG﹣GE=﹣1.
综上:CE=+1或﹣1.
【点睛】本题主要考查了等腰直角三角形的判定与性质,全等三角形的判定与性质,旋转的性质,勾股定理等知识,根据前面探索的结论解决新的问题是解题的关键.
10.(2022·河南焦作·二模)(1)如图1,在中,,,点D,E分别在边CA,CB上,且,连接AE,BD,F为AE的中点,连接CF交BD于点G,则线段CF所在直线与线段BD所在直线的位置关系是_______,线段CF和线段BD的数量关系为______.
(2)将绕点C逆时针旋转至图2所示位置时,(1)中的结论是否仍然成立 若成立,请给出证明;若不成立,请说明理由.
(3)将绕点C逆时针在平面内旋转,在旋转过程中,当B,D,E三点在同一条直线上时,CF的长为________.
【答案】(1)CF⊥BD;
(2)(1)中的结论仍然成立.理由见解析
(3)或
【分析】(1)延长CF到点M,使得FM=CF,连接AM.证,得,,所以,推出∠MAC=∠DCB=90°,再(SAS),得,,继而得到,则,故有结论CG⊥BD,BD=2CF.
(2)延长CF至M使则,连接AM,延长BC到N,先证明,得,,再证明,得,,从而得证,得到,即可得出(1)中的结论:,BD=2CF.
(3)分两种情形:如图3中,当点E在线段BD上时,如图4中,当点E在线段BD的延长线上时,分别求解即可.
【详解】解:(1)如图,延长CF至M使,则,连接AM,
∵F是AE的中点,,且,
∴,
∴,,
∴,
∴,
∵,
∴,
又∵,
∴,
∴(SAS),
∴,
∵,
∴,
∴,
∴,
故答案为:CG⊥BD,BD=2CF.
(2)证明:(1)中的结论仍然成立.
理由如下:如图,延长CF至M,使,则,连接AM,延长BC到N,
∵F是AE的中点,,且,
∴,
∴,,
∴,
∴,
∴,
又∵,,
∴,
∵,
∴,
∴,
∴,
∴,
∴,,
∵,
∴,
∴,
∴,
∴(1)中的结论:,BD=2CF仍然成立
(3)如图3中,当点E在线段BD上时,
延长CF至M使则,连接AM,
在Rt△DCE中,CD=CE=2,
∴DE=,
∵CG⊥DE,CD=CE,
∴CG平分DE,
∵∠DCE=90°,
∴DG=CG=DE=,
在Rt△CGB中,CB=6,CG=,
∴BG=,
∴BD=BG+DG=+,
由(2)知BD=2CF,
∴ CF=BD=;
如图4中,当点E在线段BD的延长线上时,
延长CF至M使则,连接AM,
在Rt△DCE中,CD=CE=2,
∴DE=,
∵CG⊥DE,CD=CE,
∴CG平分DE,
∵∠DCE=90°,
∴DG=CG=DE=,
在Rt△CGB中,CB=6,CG=,
∴BG=,
∴BD=BG-DG=-,
由(2)知BD=2CF,
∴ CF=BD=;
综上所述,满足条件的CF的值为或.
【点睛】本题考查全等三角形的判定与性质,等腰直角三角形的性质,勾股定理,本题属旋转综合题目,通过作辅助线构造全等三角形是解题的关键.
11.(2022·重庆市九年级阶段练习)【问题背景】如图1,P是等边三角形ABC外一点,∠APB=30°,则PA2+PB2=PC2.小明为了证明这个结论,将△PAB绕点A逆时针旋转60°,请根据此思路完成其证明.
【迁移应用】如图2,在等腰直角三角形ABC中,BA=BC,∠ABC=90°,点P在△ABC外部,且∠BPC=45°,若△APC的面积为5.5,求PC.
【答案】(1)【问题背景】见解析;(2)【迁移应用】
【分析】(1)【问题背景】将△PAB绕点A逆时针旋转60°得到△DAC,连接PD,由旋转及等边三角形的性质可得∠PDC=90゜,由勾股定理即可解决;
(2)【迁移应用】过B作BM⊥PB交PC的延长线于点M,连接AM,则易得△PBC≌△MBA,由全等三角形的性质易得∠AMP=90゜,再由面积条件即可求得PC的长.
【详解】(1)【问题背景】将△PAB绕点A逆时针旋转60°得到△DAC,连接PD,如图所示
由旋转的性质得:AD=PA,CD=PB,∠PAD=60゜,∠ADC=∠APB=30゜
∵AD=PA,∠PAD=60゜
∴△PAD是等边三角形
∴PD=PA,∠PDA=60゜
∴∠PDC=∠PDA+∠ADC=60゜+30゜=90゜
在Rt△PDC中,由勾股定理得:
∴
(2)【迁移应用】过B作BM⊥PB交PC的延长线于点M,连接AM,如图所示
则∠PBM=∠ABC=90゜
∴∠PBC+∠CBM=∠CBM+∠MBA
∴∠PBC=∠MBA
∵∠PBM =90゜,∠BPC=45゜
∴∠BMP=∠BPC=45゜
∴PB=MB
在△PBC和△MBA中
∴△PBC≌△MBA(SAS)
∴∠BMA=∠BPC=45゜,PC=AM
∴∠AMP=∠BMP+∠BMA=45゜+45゜=90゜
∵
∴
【点睛】本题考查了旋转的性质,等边三角形的判定与性质,全等三角形的判定与性质,等腰三角形的判定,勾股定理等知识,根据条件作图形的旋转或构造三角形全等是解决问题的关键与难点.
12.(2023·四川达州·八年级统考期末)问题发现:如图,在中,,为边所在直线上的动点(不与点、重合),连结,以为边作,且,根据,得到,结合,得出,发现线段与的数量关系为,位置关系为;
(1)探究证明:如图,在和中,,,且点在边上滑动(点不与点、重合),连接.
①则线段,,之间满足的等量关系式为_____;
②求证: ;
(2)拓展延伸:如图,在四边形中,.若,,求的长.
【答案】(1)①BC =CE+CD;②见解析;(2)AD=6.
【分析】(1)①根据题中示例方法,证明△BAD≌△CAE,得到BD=CE,从而得出BC=CE+CD;
②根据△BAD≌△CAE,得出∠ACE=45°,从而得到∠BCE=90°,则有DE2=CE2+CD2,再根据可得结论;
(2)过点A作AG⊥AD,使AG=AD,连接CG、DG,可证明△BAD≌△CAG,得到CG=BD,在直角△CDG中,根据CD的长求出DG的长,再由DG和AD的关系求出AD.
【详解】解:(1)①如图2,在Rt△ABC中,AB=AC,
∴∠B=∠ACB=45°,
∵∠BAC=∠DAE=90°,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴BD=CE,
∴ BC=BD+CD=CE+CD,
故答案为:BC=BD+CD=CE+CD.
②∵△BAD≌△CAE,
∴∠B=∠ACE=45°,
∵∠ACB=45°,
∴∠BCE=45°+45°=90°,
∴DE2=CE2+CD2,
∵AD=AE,∠DAE=90°,
∴,
∴2AD2=BD2+CD2;
(3)如图3,
过点A作AG⊥AD,使AG=AD,连接CG、DG,
则△DAG是等腰直角三角形,
∴∠ADG=45°,
∵∠ADC=45°,
∴∠GDC=90°,
同理得:△BAD≌△CAG,
∴CG=BD=13,
在Rt△CGD中,∠GDC=90°,
,
∵△DAG是等腰直角三角形,
∴,
∴AD==6.
【点睛】本题是四边形的综合题,考查的是全等三角形的判定和性质、勾股定理,掌握全等三角形的判定定理和性质定理是解题的关键.
13.(2023秋·河南南阳·八年级统考期末)综合与实践:
【问题情景】
综合与实践课上,王老师让同学们以“共顶点的等腰三角形的旋转”为主题开展数学探究活动.
【实践操作】
王老师让同学们先画出两个等边和,将绕点旋转到某一位置,要求同学们观察图形,提出问题并加以解决.
(1)如图①,“慎思组”的同学们连接、,则与有何数量关系?与有何数量关系?请你探究后直接写出结论.
(2)如图②,得知“慎思组”的结论后,“博学组”的同学们又连接,他们认为,如果,且,,就可以求出的长,请写出求解过程.
【类比探究】
(3)如图③,“智慧组”的同学们画出了两个等腰直角三角形和,其中,,;且点恰好落在上,那么、和之间一定存在某种数量关系,请你探究后直接写出它们之间的数量关系.
【答案】(1),
(2),过程见解析
(3)
【分析】(1)通过判定证明全等即可;
(2)由(1)可知边长与角度的关系,然后利用勾股定理求解即可;
(3)与(1)相同,证明全等后,利用勾股定理证明三边关系即可.
【详解】(1)证明:与均为等边三角形
又
在与中
,
(2)证明:由(1)可知 ,,
在等边中,由可得
则,
在中,
,
由勾股定理可得:
(3)连接,
,
在与中
,
【点睛】此题考查旋转模型以及勾股定理,解题关键是找准边与角的关系证明全等,然后利用勾股定理求解.
14.(2023·河南洛阳·八年级校考阶段练习)【问题发现】(1)如图1,和均为等边三角形,点B,D,E在同一直线上,连接,容易发现:①的度数为 ;②线段、之间的数量关系为 ;
【类比探究】
(2)如图2,和均为等腰直角三角形,,点B,D,E在同一直线上,连接,试判断 的度数以及线段、、之间的数量关系,并说明理由;
【问题解决】
(3)如图3,,,,,则的值为 .
【答案】(1)①;②;(2),,见解析;(3)8
【分析】(1)根据等边三角形的性质得到,得到,证明,根据全等三角形的性质证明结论;
(2)由“”可证,可得,即可求解;
(3)如图3,作辅助线构建全等三角形,由“”可证,可得,,可求,根据列方程可得x的值,最后由勾股定理可求解.
【详解】解:(1)∵和均为等边三角形,
∴,
∴,即,
在和中,
,
∴(),
∴,
∴,
故答案为:;
(2),
理由如下:∵,和均为等腰直角三角形,
∴,,
,
即,
在和中,
,
∴(),
∴,
∴,
∵,
∴;
(3)如图3,过点C作,交的延长线于F,过点B作于E,
∴,
∴四边形是矩形,
∴,
∵,
∴,
∵,
∴,
∵,
∴(),
∴,
设,则,,
∴
∴,
∴,,
∴,
∴在中,.
故答案为:.
【点睛】本题是三角形的综合题,考查的是等边三角形的性质,等腰直角三角形的性质,全等三角形的判定和性质,勾股定理等知识,掌握全等三角形的判定定理和性质定理是解题的关键.
15.(2022·福建八年级期中)如图甲,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.解答下列问题
(1)如果AB=AC,∠BAC=90°,①当点D在线段BC上时(与点B不重合),如图乙,线段CF、BD之间的位置关系为 ,数量关系为 .②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?(2)如果AB≠AC,∠BAC≠90°点D在线段BC上运动.试探究:当△ABC满足一个什么条件时,CF⊥BC(点C、F重合除外)?并说明理由.
【答案】(1)①垂直,相等;②成立,理由见解析(2)∠ACB=45°
【分析】(1)①证明△DAB≌△FAC,即可得到CF⊥BD,CF=BD.
②当点D在BC的延长线上时①的结论仍成立.由正方形ADEF的性质可推出△DAB≌△FAC,所以CF=BD,∠ACF=∠ABD.结合∠BAC=90°,AB=AC,得到∠BCF=∠ACB+∠ACF=90度.即CF⊥BD.
(2)当∠ACB=45°时,过点A作AG⊥AC交CB或CB的延长线于点G,则∠GAC=90°,可推出∠ACB=∠AGC,所以AC=AG,由(1)①可知CF⊥BD.
(1)①CF⊥BD,CF=BD
∵∠FAD=∠BAC=90°∴∠BAD=∠CAF 在△BAD与△CAF中,
∵∴△BAD≌△CAF(SAS)
∴CF=BD,∠ACF=∠ABD,
∵∴∠BCF=90°
∴CF⊥BD ;故答案为:垂直,相等;
②成立,理由如下:∵∠FAD=∠BAC=90°∴∠BAD=∠CAF
在△BAD与△CAF中,
∵,∴△BAD≌△CAF(SAS)
∴CF=BD,∠ACF=∠ACB=45°,∴∠BCF=90°,∴CF⊥BD;
(2)当∠ACB=45°时可得CF⊥BC,理由如下:
过点A作AC的垂线与CB所在直线交于G
∵∠ACB=45°∴AG=AC,∠AGC=∠ACG=45°
∵AG=AC,AD=AF,
∵∠GAD=∠GAC﹣∠DAC=90°﹣∠DAC,∠FAC=∠FAD﹣∠DAC=90°﹣∠DAC,
∴∠GAD=∠FAC,∴△GAD≌△CAF(SAS),
∴∠ACF=∠AGD=45°,∴∠GCF=∠GCA+∠ACF=90°,∴CF⊥BC.
【点睛】本题考查三角形全等的判定和直角三角形的判定,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.
15.(2022·福建福州·九年级校考期中)正方形ABCD和正方形AEFG的边长分别为3和1,将正方形AEFG绕点A逆时针旋转.
(1)当旋转至图1位置时,连接BE,DG,则线段BE和DG的关系为 ;
(2)在图1中,连接BD,BF,DF,求在旋转过程中BDF的面积最大值;
(3)在旋转过程中,当点G,E,D在同一直线上时,求线段BE的长.
【答案】(1),;(2)7.5;(3)或
【分析】(1)利用正方形的性质证明即可证得结论;
(2)连接,,,,,设交于点.利用勾股定理求出,,由推出当点F,A,K在同一直线上时,点到的最大距离,由此可得结论;
(3)分两种情形:如图中,当,,共线时,连接交于.如图中,当,,共线时,连接交于.利用勾股定理求出,可得结论.
【详解】解:(1),,理由如下:
如图1中,设交于点,交于点.
四边形、四边形都是正方形,
,,,
,
,
在和中,
,
,
,,
,
,
,
故答案为:BE=DG,BE⊥DG;
(2)如图1中,连接,,,,,设交于点.
四边形、四边形都是正方形,
,,,,
,,
,
,
当点F,A,K在同一直线上时,点到的最大距离,
的面积的最大值为;
(3)如图中,当,,共线时,连接交于.
四边形是正方形,
,,
,
,
,
,
;
如图中,当,,共线时,连接交于.
四边形是正方形,
,,
,
,
,
,;
综上所述,满足条件的的长为或.
【点睛】本题属于四边形综合题,考查了正方形的性质,全等三角形的判定和性质,勾股定理的应用等知识,解题的关键是正确寻找全等三角形解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
