浙教版数学八年级上册 1.5全等三角形的判定第3课时 “角边角”课件(共19张PPT)
文档属性
| 名称 | 浙教版数学八年级上册 1.5全等三角形的判定第3课时 “角边角”课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 659.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-09 12:09:00 | ||
图片预览



文档简介
(共19张PPT)
第一章 三角形的初步认识
1.5 全等三角形的判定
第3课时 “角边角”
学习目标
探索并理解“角边角”判定方法;
会用“角边角”判定方法证明三角形全等 ;
能用“角边角”的判定方法解决实际问题.
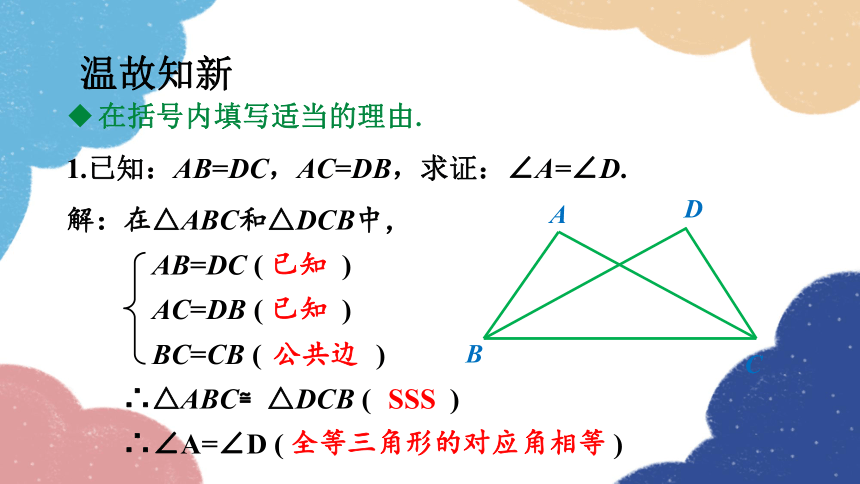
在括号内填写适当的理由.
1.已知:AB=DC,AC=DB,求证:∠A=∠D.
解:在△ABC和△DCB中,
AB=DC ( )
AC=DB ( )
BC=CB ( )
∴△ABC≌△DCB ( )
∴∠A=∠D ( )
温故知新
A
B
C
D
已知
已知
公共边
SSS
全等三角形的对应角相等
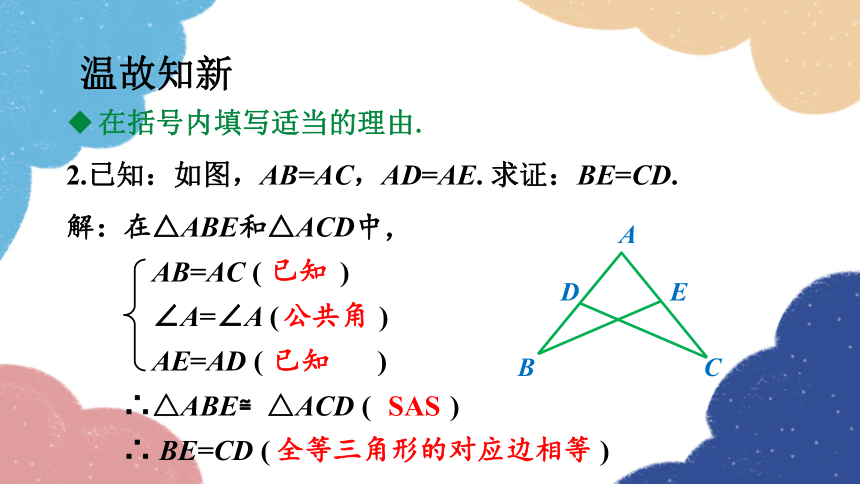
在括号内填写适当的理由.
2.已知:如图,AB=AC,AD=AE. 求证:BE=CD.
解:在△ABE和△ACD中,
AB=AC ( )
∠A=∠A ( )
AE=AD ( )
∴△ABE≌△ACD ( )
∴ BE=CD ( )
温故知新
已知
公共角
已知
SAS
全等三角形的对应边相等
B
E
A
C
D
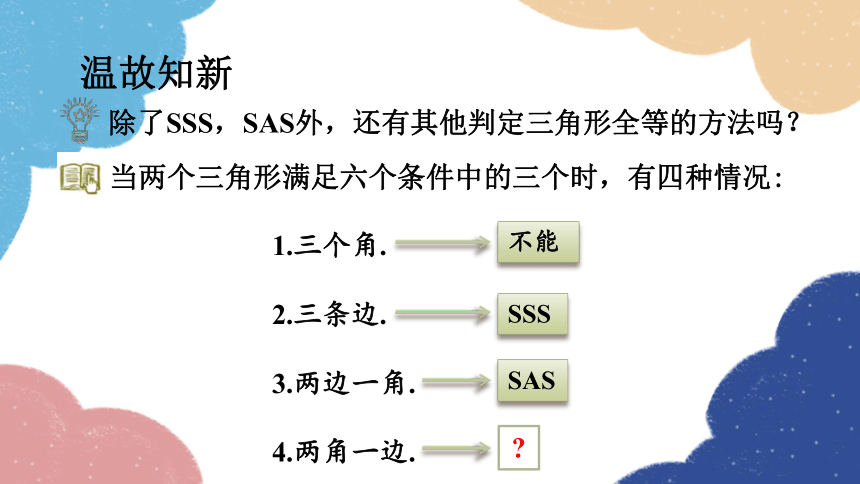
温故知新
SSS
不能
1.三个角.
2.三条边.
3.两边一角.
4.两角一边.
除了SSS,SAS外,还有其他判定三角形全等的方法吗?
当两个三角形满足六个条件中的三个时,有四种情况:
SAS
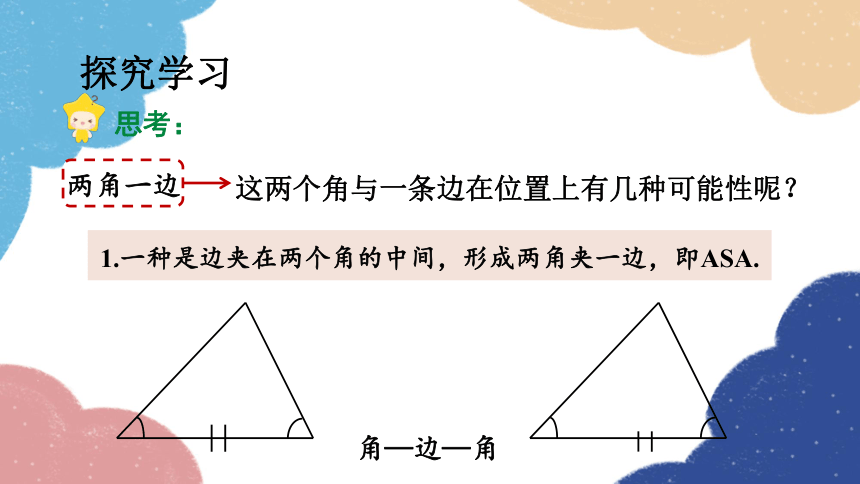
探究学习
两角一边
1.一种是边夹在两个角的中间,形成两角夹一边,即ASA.
思考:
这两个角与一条边在位置上有几种可能性呢?
角—边—角
探究学习
两角一边
2.另一种是边不夹在两角的中间,形成两角一对边,即AAS.
思考:
这两个角与一条边在位置上有几种可能性呢?
角—角—边
探究一:
角边角:若三角形的两个内角分别是60°和80°,它们所夹的边为2cm,你能画出这个三角形吗
2cm
60°
80°
探究一:
角边角:若三角形的两个内角分别是60°和80°,它们所夹的边为2cm,你能画出这个三角形吗
你画的三角形与其他同学画的一定全等吗
80°
2cm
60°
60°
两角及其夹边对应相等的两个三角形全等. 简写成“角边角”或“ASA”.
角边角(ASA)
A
B
C
A′
B′
C′
几何语言:
在△ABC 和△A′B′C′中,
∴△ABC≌△A′B′C′(ASA).
∠A =∠A′
AC =A′C′ ,
∠C =∠C′
典例讲解
例1 已知:点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C.求证:AD=AE.
证明 :在△ADC和△AEB中
∠A=∠A(公共角)
AC=AB(已知),
∠C=∠B(已知)
∴△ACD≌△ABE(ASA),
∴AD=AE(全等三角形的对应边相等).
D
B
E
A
O
C
例2 如图,AB=AC,∠ABE=∠ACD,∠BAC=∠DAE.
求证:△ABE≌△ACD.
证明:∵∠BAC=∠DAE,
∴∠BAC-∠CAE=∠DAE-∠CAE,
∠BAE=∠CAD,
AB=AC(已知),
∠ABE=∠ACD(已知),
∴∠BAE=∠CAD.
在△ABE和△ACD中,
∴△ABE≌△ACD(ASA).
例3 一块三角形玻璃碎成三片(如图),只需带上其中一块去玻璃店,玻璃店的师傅就能重新配一块与原来相同的三角形玻璃.你知道应带哪一块碎玻璃吗?请说明理由.
答:由“ASA”公理可知,只带“1”号玻璃去玻璃店,就可以买到一块完全一样的玻璃.
1.如图,已知∠1 = ∠2,∠ABC = ∠ABD. 那么AC = AD吗?为什么?
解:在△ABC和△ABD中
∠1 = ∠2(已知),
AB = AB (公共边),
∠ABC = ∠ABD (已知),
∴△ABC≌△ABD(ASA).
∴AC = AD(全等三角形对应边相等).
随堂练习
证明: ∵AB∥CD, AF∥DE,
∴∠B=∠C,∠AFB=∠DEC(两直线平行内错角相等).
∵ BE=CF,
∴BE+EF=CF+EF,即BF=CE.
在△ABF和△DCE中,
∴ △ABF≌△DCE(ASA).
2.如图,AB∥CD,AF∥DE,BE=CF. 证明: △ABF≌△DCE.
∠B=∠C
BF=CE,
∠AFB=∠DEC
2.若△ABC中,∠A=30°,∠B=70°,AB=5cm,
△DEF中,∠E=70°,∠F=80°,DE=5cm,
试说明AC与DF相等.
30°
70°
5cm
A
B
C
80°
70°
5cm
D
E
F
30°
70°
5cm
A
B
C
80°
70°
5cm
D
E
F
证明:
∵∠D=180°-∠E-∠F=180°-70°-80°=30°
∴∠A=∠D
在△ABC和△DEF中,
∠A=∠D,
AB=DE(已知),
∠B=∠E(已知),
∴△ABC≌△DEF(ASA)
∴AC=DF(全等三角形的对应边相等).
课堂小结
三角形全等的判定方法1
三边对应相等的两个三角形全等 (SSS).
三角形全等的判定方法2
两边及其夹角对应相等的两个三角形全等(SAS).
三角形全等的判定方法3
两角及其夹边对应相等的两个三角形全等(ASA).
到目前为止,我们一共探索出判定三角形全等的3种方法,它们分别是:
感谢观看!
第一章 三角形的初步认识
1.5 全等三角形的判定
第3课时 “角边角”
学习目标
探索并理解“角边角”判定方法;
会用“角边角”判定方法证明三角形全等 ;
能用“角边角”的判定方法解决实际问题.
在括号内填写适当的理由.
1.已知:AB=DC,AC=DB,求证:∠A=∠D.
解:在△ABC和△DCB中,
AB=DC ( )
AC=DB ( )
BC=CB ( )
∴△ABC≌△DCB ( )
∴∠A=∠D ( )
温故知新
A
B
C
D
已知
已知
公共边
SSS
全等三角形的对应角相等
在括号内填写适当的理由.
2.已知:如图,AB=AC,AD=AE. 求证:BE=CD.
解:在△ABE和△ACD中,
AB=AC ( )
∠A=∠A ( )
AE=AD ( )
∴△ABE≌△ACD ( )
∴ BE=CD ( )
温故知新
已知
公共角
已知
SAS
全等三角形的对应边相等
B
E
A
C
D
温故知新
SSS
不能
1.三个角.
2.三条边.
3.两边一角.
4.两角一边.
除了SSS,SAS外,还有其他判定三角形全等的方法吗?
当两个三角形满足六个条件中的三个时,有四种情况:
SAS
探究学习
两角一边
1.一种是边夹在两个角的中间,形成两角夹一边,即ASA.
思考:
这两个角与一条边在位置上有几种可能性呢?
角—边—角
探究学习
两角一边
2.另一种是边不夹在两角的中间,形成两角一对边,即AAS.
思考:
这两个角与一条边在位置上有几种可能性呢?
角—角—边
探究一:
角边角:若三角形的两个内角分别是60°和80°,它们所夹的边为2cm,你能画出这个三角形吗
2cm
60°
80°
探究一:
角边角:若三角形的两个内角分别是60°和80°,它们所夹的边为2cm,你能画出这个三角形吗
你画的三角形与其他同学画的一定全等吗
80°
2cm
60°
60°
两角及其夹边对应相等的两个三角形全等. 简写成“角边角”或“ASA”.
角边角(ASA)
A
B
C
A′
B′
C′
几何语言:
在△ABC 和△A′B′C′中,
∴△ABC≌△A′B′C′(ASA).
∠A =∠A′
AC =A′C′ ,
∠C =∠C′
典例讲解
例1 已知:点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C.求证:AD=AE.
证明 :在△ADC和△AEB中
∠A=∠A(公共角)
AC=AB(已知),
∠C=∠B(已知)
∴△ACD≌△ABE(ASA),
∴AD=AE(全等三角形的对应边相等).
D
B
E
A
O
C
例2 如图,AB=AC,∠ABE=∠ACD,∠BAC=∠DAE.
求证:△ABE≌△ACD.
证明:∵∠BAC=∠DAE,
∴∠BAC-∠CAE=∠DAE-∠CAE,
∠BAE=∠CAD,
AB=AC(已知),
∠ABE=∠ACD(已知),
∴∠BAE=∠CAD.
在△ABE和△ACD中,
∴△ABE≌△ACD(ASA).
例3 一块三角形玻璃碎成三片(如图),只需带上其中一块去玻璃店,玻璃店的师傅就能重新配一块与原来相同的三角形玻璃.你知道应带哪一块碎玻璃吗?请说明理由.
答:由“ASA”公理可知,只带“1”号玻璃去玻璃店,就可以买到一块完全一样的玻璃.
1.如图,已知∠1 = ∠2,∠ABC = ∠ABD. 那么AC = AD吗?为什么?
解:在△ABC和△ABD中
∠1 = ∠2(已知),
AB = AB (公共边),
∠ABC = ∠ABD (已知),
∴△ABC≌△ABD(ASA).
∴AC = AD(全等三角形对应边相等).
随堂练习
证明: ∵AB∥CD, AF∥DE,
∴∠B=∠C,∠AFB=∠DEC(两直线平行内错角相等).
∵ BE=CF,
∴BE+EF=CF+EF,即BF=CE.
在△ABF和△DCE中,
∴ △ABF≌△DCE(ASA).
2.如图,AB∥CD,AF∥DE,BE=CF. 证明: △ABF≌△DCE.
∠B=∠C
BF=CE,
∠AFB=∠DEC
2.若△ABC中,∠A=30°,∠B=70°,AB=5cm,
△DEF中,∠E=70°,∠F=80°,DE=5cm,
试说明AC与DF相等.
30°
70°
5cm
A
B
C
80°
70°
5cm
D
E
F
30°
70°
5cm
A
B
C
80°
70°
5cm
D
E
F
证明:
∵∠D=180°-∠E-∠F=180°-70°-80°=30°
∴∠A=∠D
在△ABC和△DEF中,
∠A=∠D,
AB=DE(已知),
∠B=∠E(已知),
∴△ABC≌△DEF(ASA)
∴AC=DF(全等三角形的对应边相等).
课堂小结
三角形全等的判定方法1
三边对应相等的两个三角形全等 (SSS).
三角形全等的判定方法2
两边及其夹角对应相等的两个三角形全等(SAS).
三角形全等的判定方法3
两角及其夹边对应相等的两个三角形全等(ASA).
到目前为止,我们一共探索出判定三角形全等的3种方法,它们分别是:
感谢观看!
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
