2023—2024学年浙教版数学八年级上册周测十四(5.5)(含答案)
文档属性
| 名称 | 2023—2024学年浙教版数学八年级上册周测十四(5.5)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 579.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-08 23:23:58 | ||
图片预览



文档简介
2023-2024学年度第一学期八年级数学(浙教版)周测十四(5.5)
学校:___________姓名:___________班级:___________考号:___________
一、选择题(共30分)
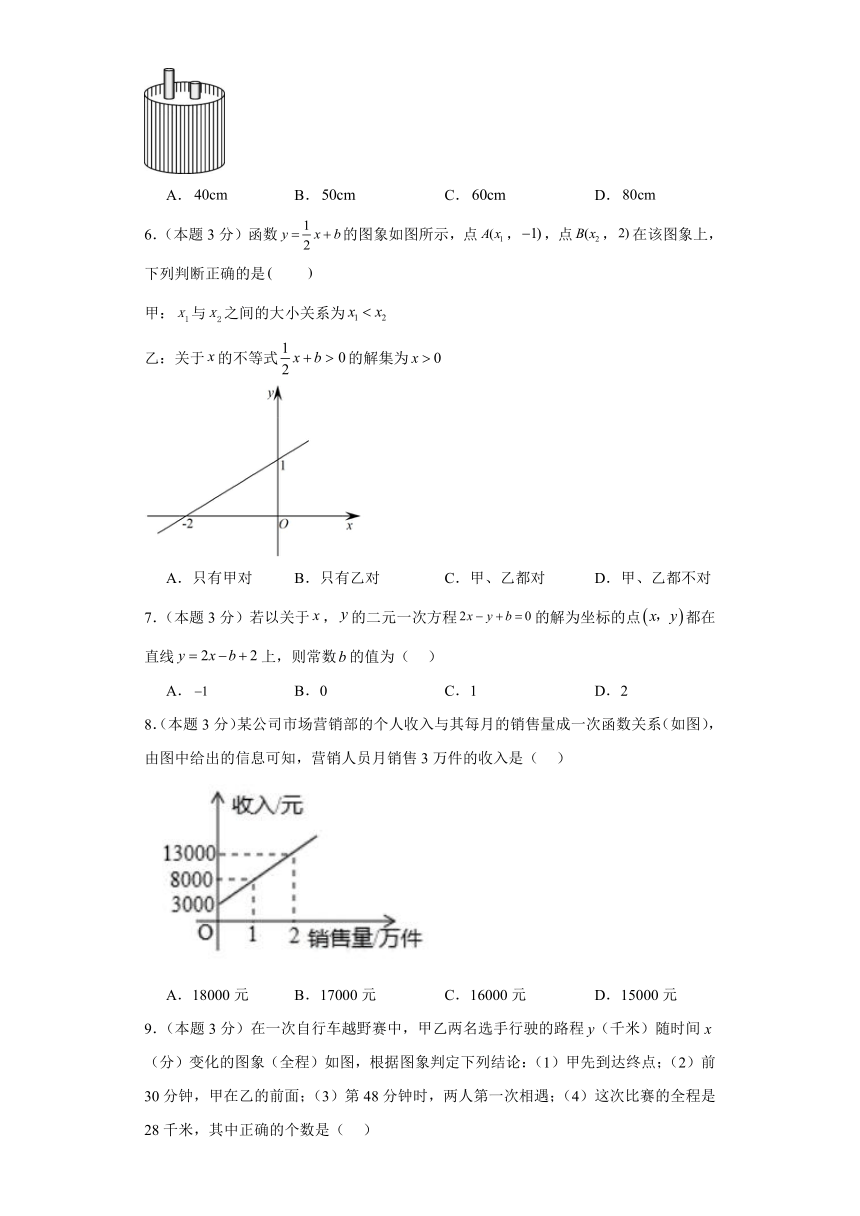
1.(本题3分)一次函数的图象如图所示,当时,的取值范围是( )
A. B. C. D.
2.(本题3分)用图象法解二元一次方程组时,小亮所画图象如图所示,则方程组的解为( )
A. B. C. D.
3.(本题3分)汽车开始行驶时,油箱内有油40升,如果每小时耗油5升,则油箱内余油量y(升)与行驶时间x(时)之间的函数关系式为( )
A. B. C. D.
4.(本题3分)已知一次函数与图象的交点是,则方程组的解为( )
A. B. C. D.
5.(本题3分)如图,两根铁棒直立于桶底水平的木桶中,在木桶中加入水后,一根高出水面的长度是它的,另一根高出水面的长度是它的.若两根铁棒长度之和为,则此时木桶中水的深度是( )
A. B. C. D.
6.(本题3分)函数的图象如图所示,点,,点,在该图象上,下列判断正确的是
甲:与之间的大小关系为
乙:关于的不等式的解集为
A.只有甲对 B.只有乙对 C.甲、乙都对 D.甲、乙都不对
7.(本题3分)若以关于,的二元一次方程的解为坐标的点都在直线上,则常数的值为( )
A. B.0 C.1 D.2
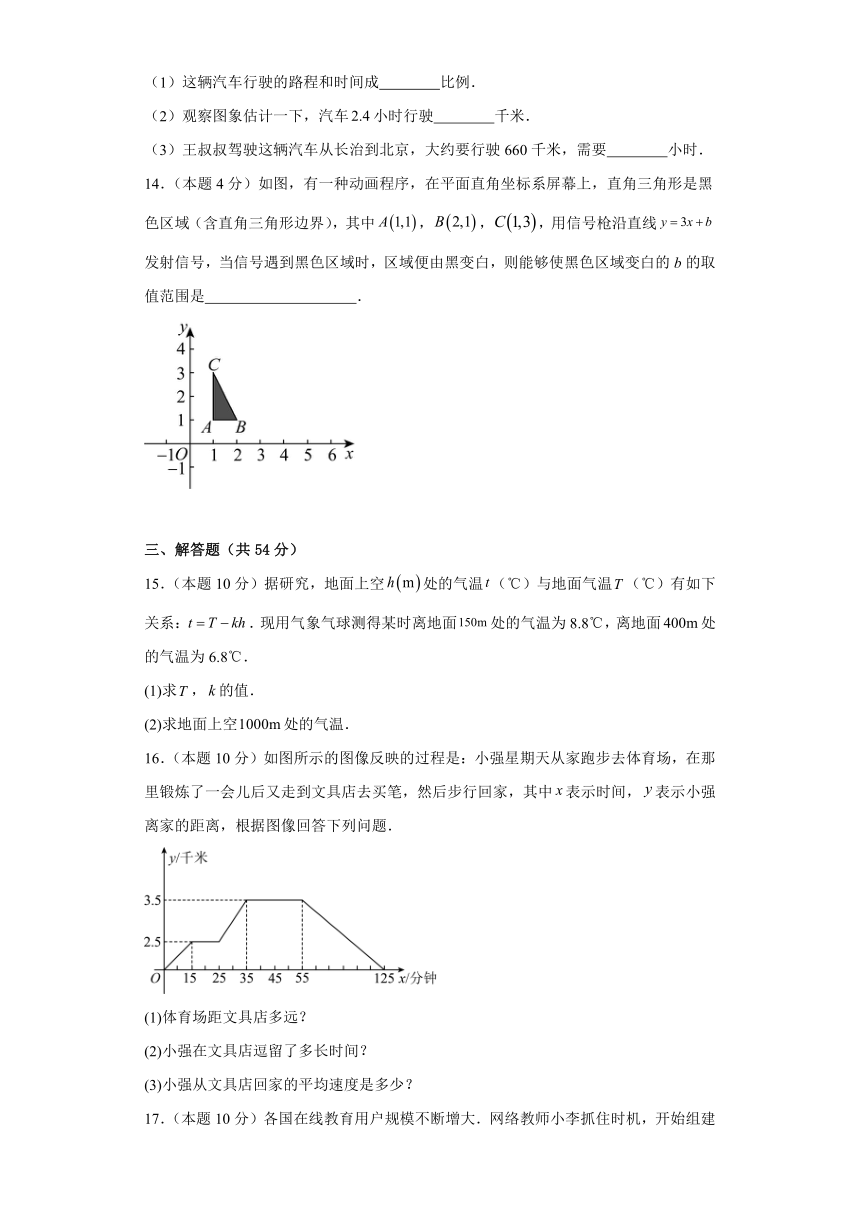
8.(本题3分)某公司市场营销部的个人收入与其每月的销售量成一次函数关系(如图),由图中给出的信息可知,营销人员月销售3万件的收入是( )
A.18000元 B.17000元 C.16000元 D.15000元
9.(本题3分)在一次自行车越野赛中,甲乙两名选手行驶的路程y(千米)随时间x(分)变化的图象(全程)如图,根据图象判定下列结论:(1)甲先到达终点;(2)前30分钟,甲在乙的前面;(3)第48分钟时,两人第一次相遇;(4)这次比赛的全程是28千米,其中正确的个数是( )
A. B. C. D.
10.(本题3分)一次函数与的图象如图所示,下列结论中正确的有( )
①对于函数来说,随的增大而减小;
②函数的图象不经过第一象限;
③;
④
A.1个 B.2个 C.3个 D.4个
二、填空题(共16分)
11.(本题4分)某市为鼓励市民节约使用燃气,对燃气进行分段收费,每月使用立方米以内(包括立方米)每立方米收费元,超过部分按每立方米元收取.如果某户的燃气使用量是立方米(超过),那么燃气费用与的函数关系式是 .
12.(本题4分)一次函数的图象与轴的交点A的坐标为,与轴的交点为,在轴上有一点,且的面积为5,求的坐标为 .
13.(本题4分)右面是一辆汽车从长治到北京所行驶路程和时间的图象.
(1)这辆汽车行驶的路程和时间成 比例.
(2)观察图象估计一下,汽车小时行驶 千米.
(3)王叔叔驾驶这辆汽车从长治到北京,大约要行驶660千米,需要 小时.
14.(本题4分)如图,有一种动画程序,在平面直角坐标系屏幕上,直角三角形是黑色区域(含直角三角形边界),其中,,,用信号枪沿直线发射信号,当信号遇到黑色区域时,区域便由黑变白,则能够使黑色区域变白的b的取值范围是 .
三、解答题(共54分)
15.(本题10分)据研究,地面上空处的气温(℃)与地面气温(℃)有如下关系:.现用气象气球测得某时离地面处的气温为8.8℃,离地面处的气温为6.8℃.
(1)求,的值.
(2)求地面上空处的气温.
16.(本题10分)如图所示的图像反映的过程是:小强星期天从家跑步去体育场,在那里锻炼了一会儿后又走到文具店去买笔,然后步行回家,其中表示时间,表示小强离家的距离,根据图像回答下列问题.
(1)体育场距文具店多远?
(2)小强在文具店逗留了多长时间?
(3)小强从文具店回家的平均速度是多少?
17.(本题10分)各国在线教育用户规模不断增大.网络教师小李抓住时机,开始组建团队,制作面向两个不同需求学生群体的微课视频.已知制作3个A类微课和5个B类微课需要元成本,制作5个A类微课和10个B类微课需要元成本.李老师又把做好的微课出售给某视频播放网站,每个A类微课售价元,每个B类微课售价元.该团队每天可以制作1个A类微课或者个B类微课,且团队每月制作的B类微课数不少于A类微课数的2倍(注:每月制作的两类微课的个数均为整数).假设团队每月有天制作微课,其中制作A类微课a天,制作两类微课的月利润为w元.
(1)求团队制作一个A类微课和一个B类微课的成本分别是多少元?
(2)求w与a之间的函数关系式,并写出a的取值范围;
(3)每月制作A类微课多少个时,该团队月利润w最大,最大利润是多少元?
18.(本题12分)如图,根据图中信息回答下列问题:
(1)关于的不等式的解集是______;
(2)关于的不等式的解集是______;
(3)当时,的取值范围是______.
19.(本题12分)如图,在平面直角坐标系中,直线与轴,轴分别交于点,点,点在轴的负半轴上,若将沿直线折叠,点恰好落在轴正半轴上的点处.
(1)直接写出点,,的坐标;
(2)求直线的解析式;
(3)直线与直线相交于点,求的面积.
参考答案:
1.B
2.A
3.D
4.D
5.C
6.A
7.C
8.A
9.C
10.C
11.
12.或
13. 正 192 /
14.
15.(1)解:根据题意列方程组
解得,.
(2)解:由(1)得:.
故当时,℃
16.(1)解:由图像看出体育场距文具店(千米).
(2)解:由图像看出小强在文具店逗留了(分).
(3)解:文具店到家的距离是千米,小强回家的时间为分钟,
∴小强从文具店回家的平均速度是(千米/分).
17.(1)解:设团队制作一个类微课的成本为元,制作一个类微课的成本为元,根据题意得:
,
解得,
团队制作一个类微课的成本为元,制作一个类微课的成本为元;
(2)解:由题意得;
;
解得,
每月制作的两类微课的个数均为整数,
的值为:;
(3)解:由(2)得:,
,
随的增大而增大,
当时,有最大值,
(元),
每月制作类微课8个时,该团队月利润最大,最大利润是元.
18.(1)∵直线与x轴的交点是,且随着x的增大而减小,
∴当时,,即不等式的解集是;
故答案是:;
(2)∵直线与y轴的交点是,且随着x的增大而增大,
∴当时,,即不等式的解集是;
故答案是:;
(3)由一次函数的图象知,两条直线的交点坐标是,
当函数的图象在的下面时,有;当时,,
所以当时,;
故答案为:;
19.(1)当时,,
∴B点的坐标为,
∴,
当,则,解得,
∵A点的坐标为,
∴,
∴,
∵折叠,
∴,
∴,
∴,
(2)设点,则,
在中,
,
即,
解得,
∴,
设直线的解析式为,
则
解得.
∴直线的解析式为.
(3)解:如图所示,
∵直线与直线相交于点
联立
解得:
∴
∵,,,,
∴, ,
∴
.
学校:___________姓名:___________班级:___________考号:___________
一、选择题(共30分)
1.(本题3分)一次函数的图象如图所示,当时,的取值范围是( )
A. B. C. D.
2.(本题3分)用图象法解二元一次方程组时,小亮所画图象如图所示,则方程组的解为( )
A. B. C. D.
3.(本题3分)汽车开始行驶时,油箱内有油40升,如果每小时耗油5升,则油箱内余油量y(升)与行驶时间x(时)之间的函数关系式为( )
A. B. C. D.
4.(本题3分)已知一次函数与图象的交点是,则方程组的解为( )
A. B. C. D.
5.(本题3分)如图,两根铁棒直立于桶底水平的木桶中,在木桶中加入水后,一根高出水面的长度是它的,另一根高出水面的长度是它的.若两根铁棒长度之和为,则此时木桶中水的深度是( )
A. B. C. D.
6.(本题3分)函数的图象如图所示,点,,点,在该图象上,下列判断正确的是
甲:与之间的大小关系为
乙:关于的不等式的解集为
A.只有甲对 B.只有乙对 C.甲、乙都对 D.甲、乙都不对
7.(本题3分)若以关于,的二元一次方程的解为坐标的点都在直线上,则常数的值为( )
A. B.0 C.1 D.2
8.(本题3分)某公司市场营销部的个人收入与其每月的销售量成一次函数关系(如图),由图中给出的信息可知,营销人员月销售3万件的收入是( )
A.18000元 B.17000元 C.16000元 D.15000元
9.(本题3分)在一次自行车越野赛中,甲乙两名选手行驶的路程y(千米)随时间x(分)变化的图象(全程)如图,根据图象判定下列结论:(1)甲先到达终点;(2)前30分钟,甲在乙的前面;(3)第48分钟时,两人第一次相遇;(4)这次比赛的全程是28千米,其中正确的个数是( )
A. B. C. D.
10.(本题3分)一次函数与的图象如图所示,下列结论中正确的有( )
①对于函数来说,随的增大而减小;
②函数的图象不经过第一象限;
③;
④
A.1个 B.2个 C.3个 D.4个
二、填空题(共16分)
11.(本题4分)某市为鼓励市民节约使用燃气,对燃气进行分段收费,每月使用立方米以内(包括立方米)每立方米收费元,超过部分按每立方米元收取.如果某户的燃气使用量是立方米(超过),那么燃气费用与的函数关系式是 .
12.(本题4分)一次函数的图象与轴的交点A的坐标为,与轴的交点为,在轴上有一点,且的面积为5,求的坐标为 .
13.(本题4分)右面是一辆汽车从长治到北京所行驶路程和时间的图象.
(1)这辆汽车行驶的路程和时间成 比例.
(2)观察图象估计一下,汽车小时行驶 千米.
(3)王叔叔驾驶这辆汽车从长治到北京,大约要行驶660千米,需要 小时.
14.(本题4分)如图,有一种动画程序,在平面直角坐标系屏幕上,直角三角形是黑色区域(含直角三角形边界),其中,,,用信号枪沿直线发射信号,当信号遇到黑色区域时,区域便由黑变白,则能够使黑色区域变白的b的取值范围是 .
三、解答题(共54分)
15.(本题10分)据研究,地面上空处的气温(℃)与地面气温(℃)有如下关系:.现用气象气球测得某时离地面处的气温为8.8℃,离地面处的气温为6.8℃.
(1)求,的值.
(2)求地面上空处的气温.
16.(本题10分)如图所示的图像反映的过程是:小强星期天从家跑步去体育场,在那里锻炼了一会儿后又走到文具店去买笔,然后步行回家,其中表示时间,表示小强离家的距离,根据图像回答下列问题.
(1)体育场距文具店多远?
(2)小强在文具店逗留了多长时间?
(3)小强从文具店回家的平均速度是多少?
17.(本题10分)各国在线教育用户规模不断增大.网络教师小李抓住时机,开始组建团队,制作面向两个不同需求学生群体的微课视频.已知制作3个A类微课和5个B类微课需要元成本,制作5个A类微课和10个B类微课需要元成本.李老师又把做好的微课出售给某视频播放网站,每个A类微课售价元,每个B类微课售价元.该团队每天可以制作1个A类微课或者个B类微课,且团队每月制作的B类微课数不少于A类微课数的2倍(注:每月制作的两类微课的个数均为整数).假设团队每月有天制作微课,其中制作A类微课a天,制作两类微课的月利润为w元.
(1)求团队制作一个A类微课和一个B类微课的成本分别是多少元?
(2)求w与a之间的函数关系式,并写出a的取值范围;
(3)每月制作A类微课多少个时,该团队月利润w最大,最大利润是多少元?
18.(本题12分)如图,根据图中信息回答下列问题:
(1)关于的不等式的解集是______;
(2)关于的不等式的解集是______;
(3)当时,的取值范围是______.
19.(本题12分)如图,在平面直角坐标系中,直线与轴,轴分别交于点,点,点在轴的负半轴上,若将沿直线折叠,点恰好落在轴正半轴上的点处.
(1)直接写出点,,的坐标;
(2)求直线的解析式;
(3)直线与直线相交于点,求的面积.
参考答案:
1.B
2.A
3.D
4.D
5.C
6.A
7.C
8.A
9.C
10.C
11.
12.或
13. 正 192 /
14.
15.(1)解:根据题意列方程组
解得,.
(2)解:由(1)得:.
故当时,℃
16.(1)解:由图像看出体育场距文具店(千米).
(2)解:由图像看出小强在文具店逗留了(分).
(3)解:文具店到家的距离是千米,小强回家的时间为分钟,
∴小强从文具店回家的平均速度是(千米/分).
17.(1)解:设团队制作一个类微课的成本为元,制作一个类微课的成本为元,根据题意得:
,
解得,
团队制作一个类微课的成本为元,制作一个类微课的成本为元;
(2)解:由题意得;
;
解得,
每月制作的两类微课的个数均为整数,
的值为:;
(3)解:由(2)得:,
,
随的增大而增大,
当时,有最大值,
(元),
每月制作类微课8个时,该团队月利润最大,最大利润是元.
18.(1)∵直线与x轴的交点是,且随着x的增大而减小,
∴当时,,即不等式的解集是;
故答案是:;
(2)∵直线与y轴的交点是,且随着x的增大而增大,
∴当时,,即不等式的解集是;
故答案是:;
(3)由一次函数的图象知,两条直线的交点坐标是,
当函数的图象在的下面时,有;当时,,
所以当时,;
故答案为:;
19.(1)当时,,
∴B点的坐标为,
∴,
当,则,解得,
∵A点的坐标为,
∴,
∴,
∵折叠,
∴,
∴,
∴,
(2)设点,则,
在中,
,
即,
解得,
∴,
设直线的解析式为,
则
解得.
∴直线的解析式为.
(3)解:如图所示,
∵直线与直线相交于点
联立
解得:
∴
∵,,,,
∴, ,
∴
.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
