2023—2024学年浙教版数学八年级上册周测六(2.6—2.8)(含答案)
文档属性
| 名称 | 2023—2024学年浙教版数学八年级上册周测六(2.6—2.8)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 660.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-09 17:38:56 | ||
图片预览


文档简介
2023-2024学年度第一学期八年级数学(浙教版)周测七(2.6—2.8)
学校:___________姓名:___________班级:___________考号:___________
一、选择题(共30分)
1.(本题3分)若直角三角形的一个锐角等于,则它的另外一个锐角等于( )
A. B. C. D.
2.(本题3分)以下列各组数为边长,不能构成直角三角形的是( )
A., B.,, C.,, D.,,
3.(本题3分)如图,已知,,.则的理由是( )
A. B. C. D.
4.(本题3分)如图,在中,,为边上的中线,过点作于点,,则的度数为( )
A. B. C. D.
5.(本题3分)若a,b,c是的三边长,则下列条件不能判定为直角三角形的是( )
A. B.
C. D.
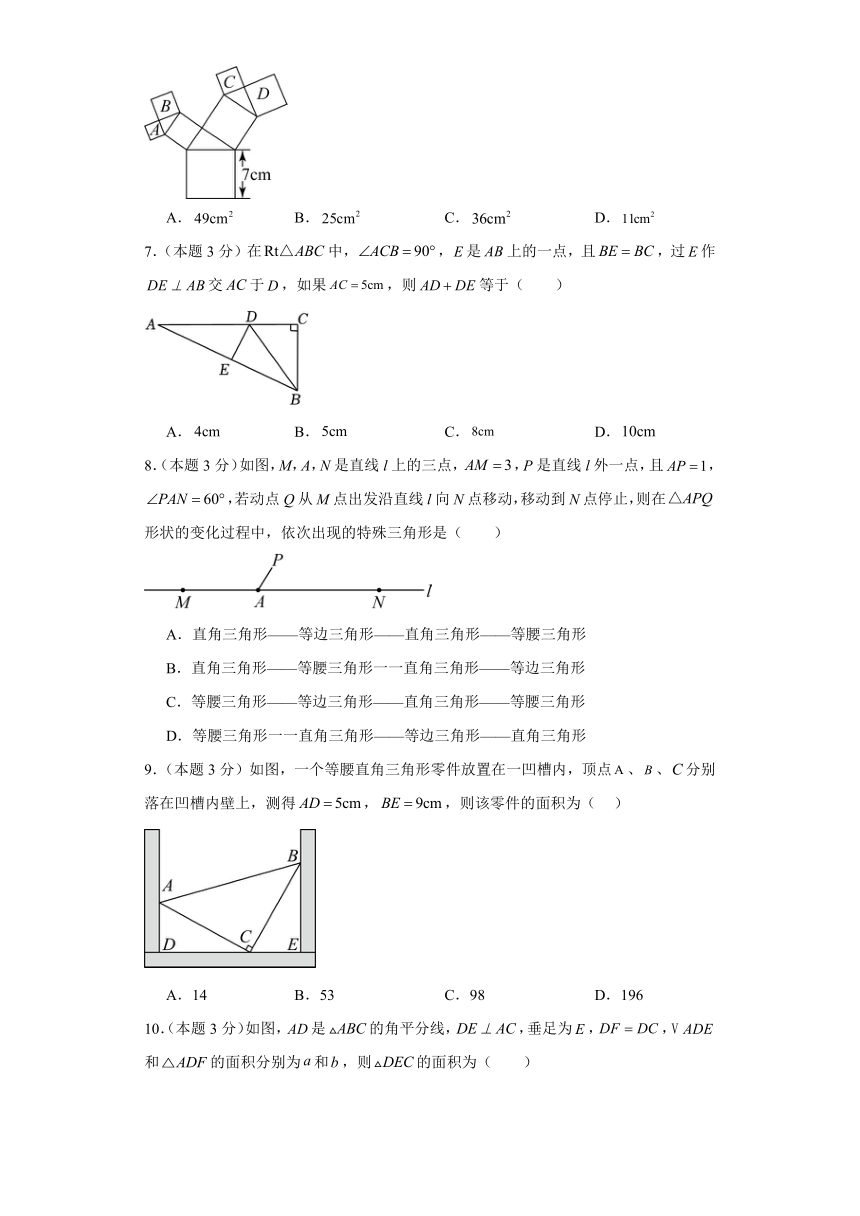
6.(本题3分)如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7 cm,则正方形A、B、C、D的面积的和是( )
A. B. C. D.
7.(本题3分)在中,,是上的一点,且,过作交于,如果,则等于( )
A. B. C. D.
8.(本题3分)如图,M,A,N是直线l上的三点,,P是直线l外一点,且,,若动点Q从M点出发沿直线l向N点移动,移动到N点停止,则在形状的变化过程中,依次出现的特殊三角形是( )
A.直角三角形——等边三角形——直角三角形——等腰三角形
B.直角三角形——等腰三角形一一直角三角形——等边三角形
C.等腰三角形——等边三角形——直角三角形——等腰三角形
D.等腰三角形一一直角三角形——等边三角形——直角三角形
9.(本题3分)如图,一个等腰直角三角形零件放置在一凹槽内,顶点、、分别落在凹槽内壁上,测得,,则该零件的面积为( )
A.14 B.53 C.98 D.196
10.(本题3分)如图,是的角平分线,,垂足为,,和的面积分别为和,则的面积为( )
A. B. C. D.
二、填空题(共16分)
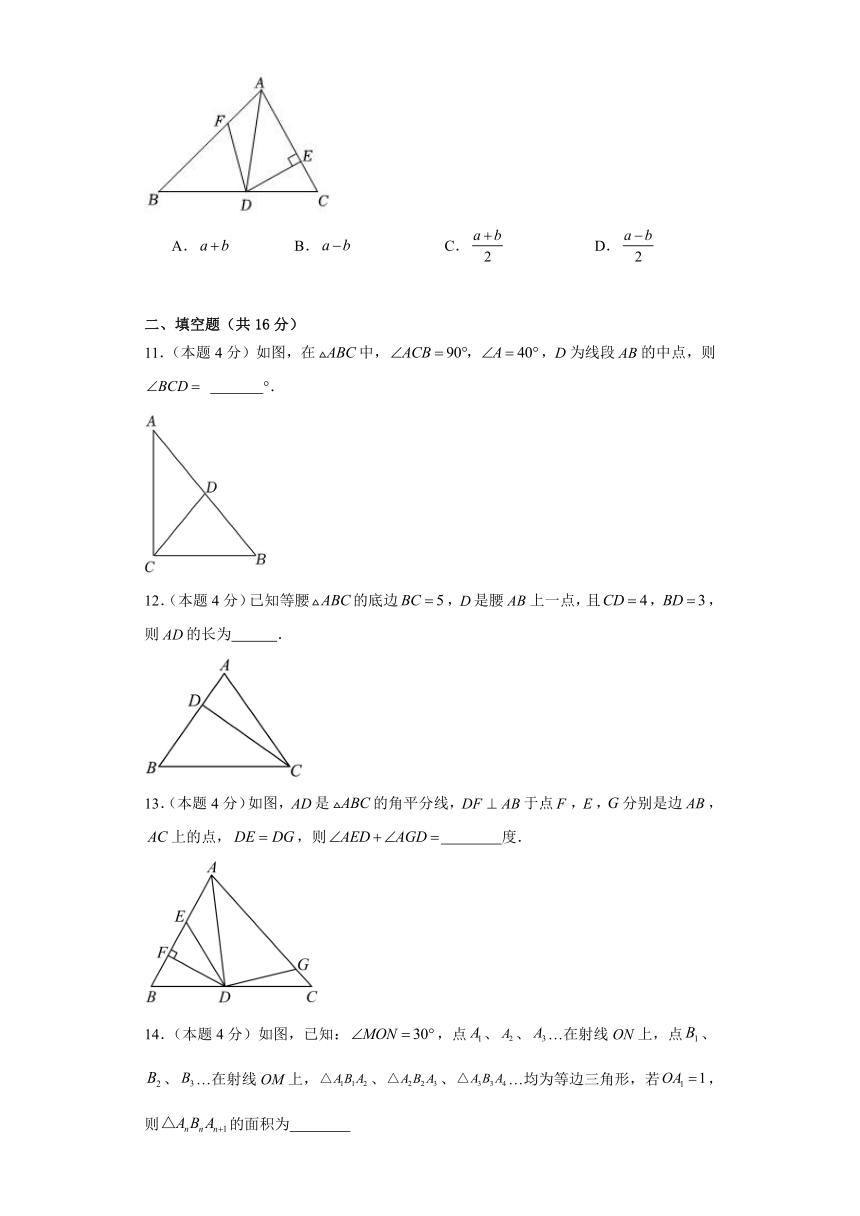
11.(本题4分)如图,在中,,D为线段的中点,则 °.
12.(本题4分)已知等腰的底边,是腰上一点,且,,则的长为 .
13.(本题4分)如图,是的角平分线,于点,,分别是边,上的点,,则 度.
14.(本题4分)如图,已知:,点、、…在射线ON上,点、、…在射线OM上,、、…均为等边三角形,若,则的面积为
三、解答题(共54分)
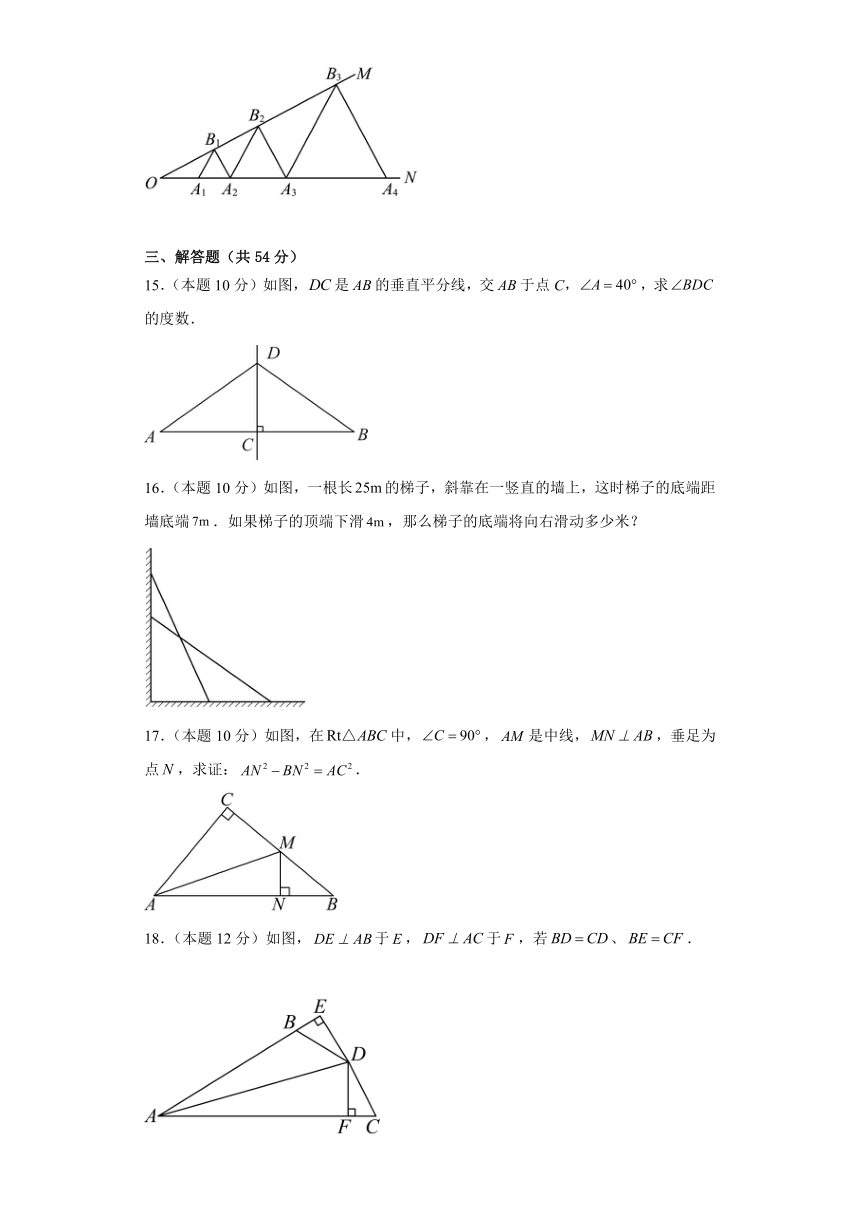
15.(本题10分)如图,是的垂直平分线,交于点C,,求的度数.
16.(本题10分)如图,一根长的梯子,斜靠在一竖直的墙上,这时梯子的底端距墙底端.如果梯子的顶端下滑,那么梯子的底端将向右滑动多少米?
17.(本题10分)如图,在中,,是中线,,垂足为点,求证:.
18.(本题12分)如图,于,于,若、.
(1)求证:平分;
(2)已知,,求的长.
19.(本题12分)(1)问题再现:学习二次根式时,老师给同学们提出了一个求代数式最小值的问题,如,“求代数式的最小值”.小强同学发现可看作两直角边分别为x和2的直角三角形斜边长,可看作两直角边分别是和4的直角三角形的斜边长.于是构造出如图所示,将问题转化为求线段AB的长,进而求得的最小值是______.
(2)类比迁移:已知a,b均为正数,且.求的最小值.
(3)方法应用:已知a,b均为正数,且,,是三角形的三边长,求这个三角形的面积(用含a,b的代数式表示).
参考答案:
1.B
2.D
3.A
4.A
5.B
6.A
7.B
8.D
9.B
10.B
11.50
12./
13.
14.
15.解:∵是的垂直平分线,
∴,
∴,
∴在中,.
16.解:如图,
由题意得:,
在中,,
∴,
在中,,
∴,
答:梯子的底端将向右滑动米.
17.解:证明:于,
,
,
又,
,
又,
,
即.
18.(1)解:证明:,,
,
在与中,
,
,
,
又,,
平分;
(2),,
,
,
,
在与中,
,
,
,
.
19.解:(1)如图所示,,,,,
在直角三角形中,,
在直角三角形中,,
∴,
∴要想的值最小,则的值最小,
∴当A、D、B三点共线时,的值最小,最小值为,
过点B作交延长线于F,
∵,,,
∴由长方形的性质得,,
∴,
∴,
∴的最小值为10,
故答案为:10;
(2)如图所示,,,,,
在直角三角形中,,
在直角三角形中,,
∴,
∴要想的值最小,则的值最小,
∴当A、D、B三点共线时,的值最小,最小值为,
过点B作交延长线于F,
∵,,,
∴由长方形的性质,,
∴,
∴,
∴的最小值为13,
故答案为:13;
(3)如图所示,,,,
,
∴,,,
∴的面积即为所求,
∴
.
学校:___________姓名:___________班级:___________考号:___________
一、选择题(共30分)
1.(本题3分)若直角三角形的一个锐角等于,则它的另外一个锐角等于( )
A. B. C. D.
2.(本题3分)以下列各组数为边长,不能构成直角三角形的是( )
A., B.,, C.,, D.,,
3.(本题3分)如图,已知,,.则的理由是( )
A. B. C. D.
4.(本题3分)如图,在中,,为边上的中线,过点作于点,,则的度数为( )
A. B. C. D.
5.(本题3分)若a,b,c是的三边长,则下列条件不能判定为直角三角形的是( )
A. B.
C. D.
6.(本题3分)如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7 cm,则正方形A、B、C、D的面积的和是( )
A. B. C. D.
7.(本题3分)在中,,是上的一点,且,过作交于,如果,则等于( )
A. B. C. D.
8.(本题3分)如图,M,A,N是直线l上的三点,,P是直线l外一点,且,,若动点Q从M点出发沿直线l向N点移动,移动到N点停止,则在形状的变化过程中,依次出现的特殊三角形是( )
A.直角三角形——等边三角形——直角三角形——等腰三角形
B.直角三角形——等腰三角形一一直角三角形——等边三角形
C.等腰三角形——等边三角形——直角三角形——等腰三角形
D.等腰三角形一一直角三角形——等边三角形——直角三角形
9.(本题3分)如图,一个等腰直角三角形零件放置在一凹槽内,顶点、、分别落在凹槽内壁上,测得,,则该零件的面积为( )
A.14 B.53 C.98 D.196
10.(本题3分)如图,是的角平分线,,垂足为,,和的面积分别为和,则的面积为( )
A. B. C. D.
二、填空题(共16分)
11.(本题4分)如图,在中,,D为线段的中点,则 °.
12.(本题4分)已知等腰的底边,是腰上一点,且,,则的长为 .
13.(本题4分)如图,是的角平分线,于点,,分别是边,上的点,,则 度.
14.(本题4分)如图,已知:,点、、…在射线ON上,点、、…在射线OM上,、、…均为等边三角形,若,则的面积为
三、解答题(共54分)
15.(本题10分)如图,是的垂直平分线,交于点C,,求的度数.
16.(本题10分)如图,一根长的梯子,斜靠在一竖直的墙上,这时梯子的底端距墙底端.如果梯子的顶端下滑,那么梯子的底端将向右滑动多少米?
17.(本题10分)如图,在中,,是中线,,垂足为点,求证:.
18.(本题12分)如图,于,于,若、.
(1)求证:平分;
(2)已知,,求的长.
19.(本题12分)(1)问题再现:学习二次根式时,老师给同学们提出了一个求代数式最小值的问题,如,“求代数式的最小值”.小强同学发现可看作两直角边分别为x和2的直角三角形斜边长,可看作两直角边分别是和4的直角三角形的斜边长.于是构造出如图所示,将问题转化为求线段AB的长,进而求得的最小值是______.
(2)类比迁移:已知a,b均为正数,且.求的最小值.
(3)方法应用:已知a,b均为正数,且,,是三角形的三边长,求这个三角形的面积(用含a,b的代数式表示).
参考答案:
1.B
2.D
3.A
4.A
5.B
6.A
7.B
8.D
9.B
10.B
11.50
12./
13.
14.
15.解:∵是的垂直平分线,
∴,
∴,
∴在中,.
16.解:如图,
由题意得:,
在中,,
∴,
在中,,
∴,
答:梯子的底端将向右滑动米.
17.解:证明:于,
,
,
又,
,
又,
,
即.
18.(1)解:证明:,,
,
在与中,
,
,
,
又,,
平分;
(2),,
,
,
,
在与中,
,
,
,
.
19.解:(1)如图所示,,,,,
在直角三角形中,,
在直角三角形中,,
∴,
∴要想的值最小,则的值最小,
∴当A、D、B三点共线时,的值最小,最小值为,
过点B作交延长线于F,
∵,,,
∴由长方形的性质得,,
∴,
∴,
∴的最小值为10,
故答案为:10;
(2)如图所示,,,,,
在直角三角形中,,
在直角三角形中,,
∴,
∴要想的值最小,则的值最小,
∴当A、D、B三点共线时,的值最小,最小值为,
过点B作交延长线于F,
∵,,,
∴由长方形的性质,,
∴,
∴,
∴的最小值为13,
故答案为:13;
(3)如图所示,,,,
,
∴,,,
∴的面积即为所求,
∴
.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
