浙教版数学八年级上册 1.5全等三角形的判定 第1课时“边边边”课件(共25张PPT)
文档属性
| 名称 | 浙教版数学八年级上册 1.5全等三角形的判定 第1课时“边边边”课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-09 12:47:28 | ||
图片预览



文档简介
(共25张PPT)
第一章 三角形的初步认识
1.5 全等三角形的判定
第1课时 “边边边”
学习目标
探索并理解“边边边”判定方法,会用“边边边”判定方法证明三角形全等;
了解三角形的稳定性及其应用;
会用尺规作已知角的角平分线,了解作图的道理.
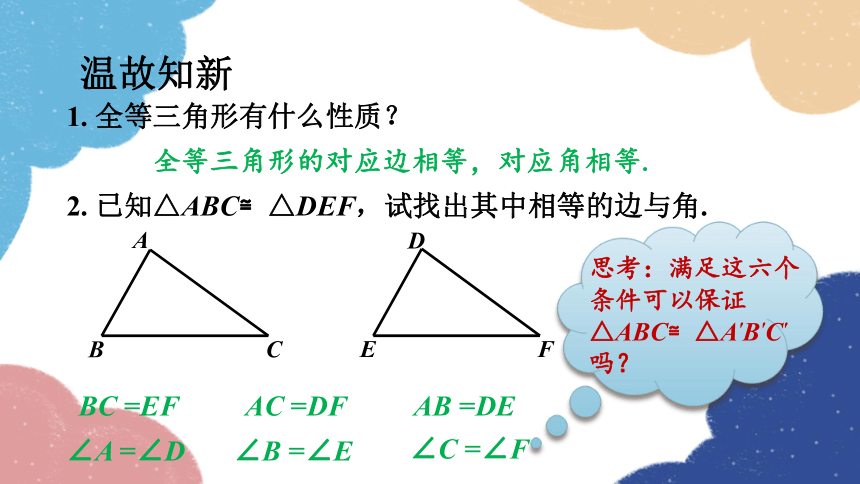
温故知新
1. 全等三角形有什么性质?
全等三角形的对应边相等,对应角相等.
2. 已知△ABC≌△DEF,试找出其中相等的边与角.
∠A =∠D
AB =DE
∠B =∠E
BC =EF
∠C =∠F
AC =DF
思考:满足这六个条件可以保证△ABC≌△A′B′C′吗?
A
B
C
D
E
F
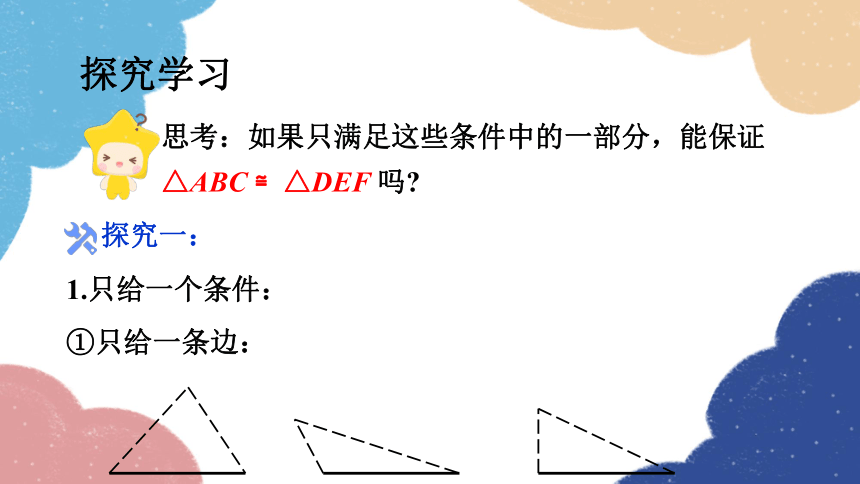
探究学习
1.只给一个条件:
①只给一条边:
探究一:
思考:如果只满足这些条件中的一部分,能保证△ABC ≌△DEF 吗
②只给一个角:
1.只给一个条件:
60°
60°
60°
探究一:
结论:
只有一条边或一个角对应相等的两个三角形不一定全等.
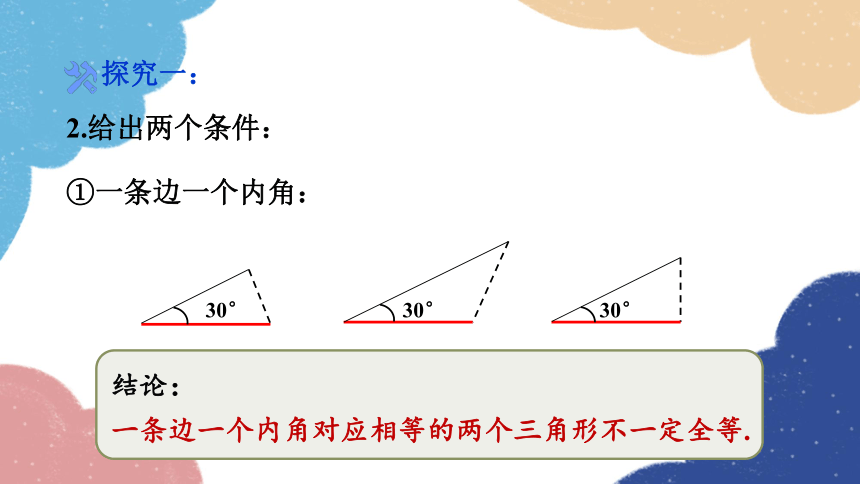
2.给出两个条件:
①一条边一个内角:
30°
30°
30°
探究一:
结论:
一条边一个内角对应相等的两个三角形不一定全等.
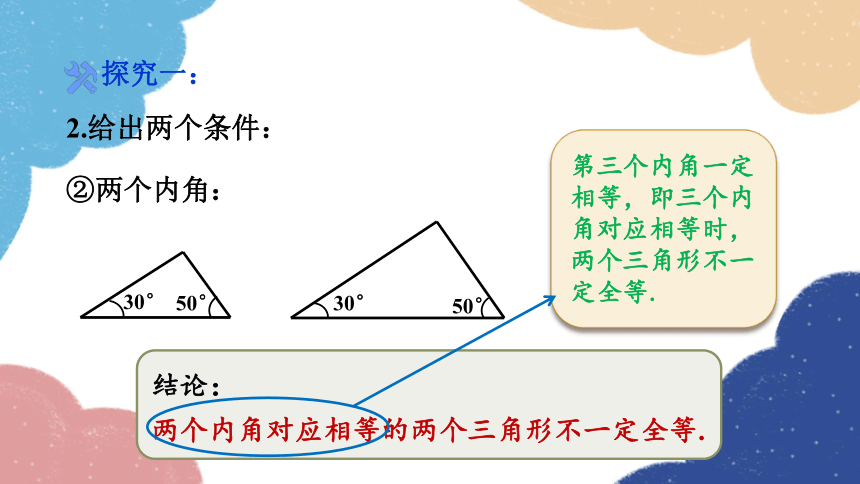
2.给出两个条件:
探究一:
②两个内角:
30°
50°
结论:
两个内角对应相等的两个三角形不一定全等.
50°
30°
第三个内角一定相等,即三个内角对应相等时,两个三角形不一定全等.
2.给出两个条件:
探究一:
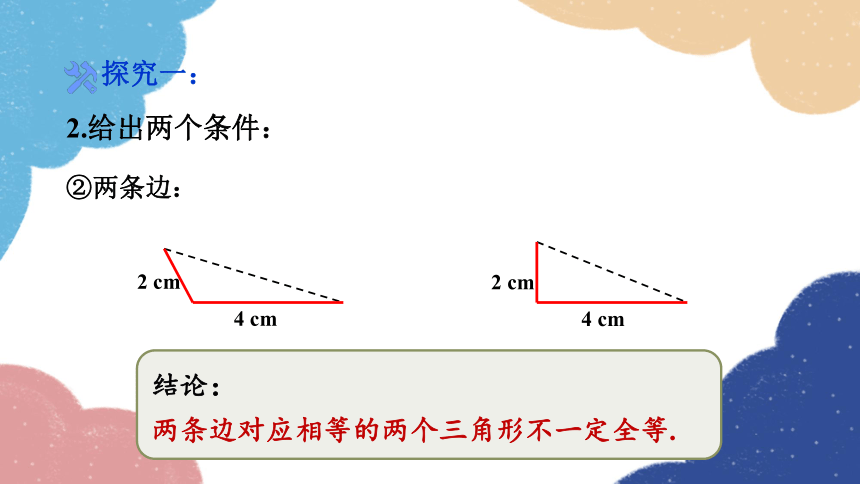
②两条边:
结论:
两条边对应相等的两个三角形不一定全等.
2 cm
4 cm
2 cm
4 cm
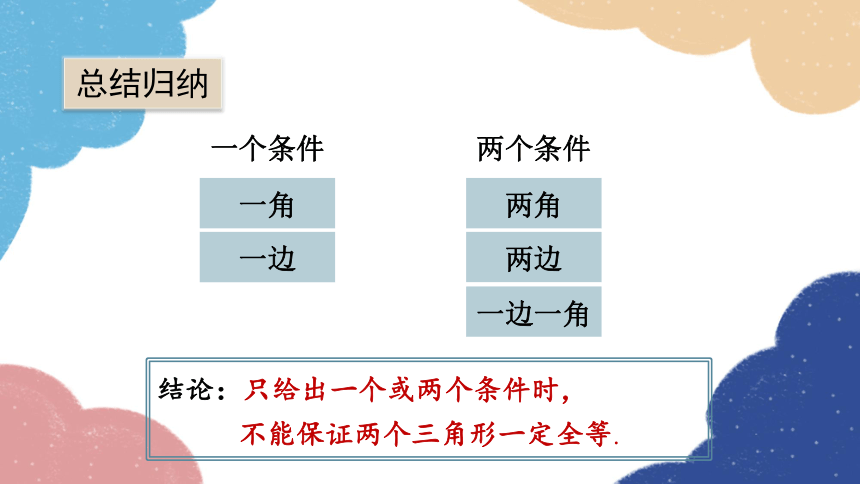
结论:只给出一个或两个条件时,
不能保证两个三角形一定全等.
一边一角
一边
总结归纳
一个条件
一角
两个条件
两角
两边
① 三个角;
② 三条边;
③ 两条边一个内角;
④ 两个内角一条边.
两个条件的探究中,已发现不能保证三角形全等.
① 三个角;
交流讨论:
如果满足三个条件,你能说出有哪几种可能的情况?
先任意画出一个△ABC,再画出一个△A′B′C′ ,使A′B′=
AB,B′C′=BC,A′C′=AC. 把画好的△A′B′C′剪下,放到△ABC上,它们全等吗?
A
B
C
探究二:
画法:
1.画线段 B′C′=BC;
2.分别以 B′ 、C′为圆心,BA、
BC为半径画弧,两弧交于点A′;
3. 连接线段 A′B′, A′C′,得到△A′B′C′.
B′
C′
A′
先任意画出一个△ABC,再画出一个△A′B′C′ ,使A′B′=
AB,B′C′=BC,A′C′=AC. 把画好的△A′B′C′剪下,放到△ABC上,它们全等吗?
把画好的△A′B′C′剪下,放到△ABC上.
两个三角形完全重合,说明△ABC 与△A′B′C′全等.
A
B
C
B′
A′
C′
探究二:
三边对应相等的两个三角形全等,
简写为“边边边”或“SSS”.
注:这说明只要三角形三边的长度确定了,这个三角形的形状和大小就完全确定了.此定理也是三角形具有稳定性的原理.
边边边(SSS)
例1 如图:AB=AC,AE=AD,BD=CE,说明△AEB≌△ADC.
C
A
B
D
E
解: ∵BD=CE,
∴BD-ED=CE-ED,即BE=CD.
BE=CD
AB=AC (已知) , AE=AD (已知)
分析:两个三角形中已知两组对应边相等,只需要再说明第三组对应边相等即可.
在△AEB和△ADC中,
∴△AEB≌△ADC (SSS).
典例精讲
探究学习
多边形不稳定
三角形具有稳定性
探究三:
你能举例说明三角形的稳定性在实际生活中的应用吗?
性质应用
典例精讲
例2 要使下列木架不变形各至少需要多少根木条
1根
2根
3根
将多边形变成稳定图形的原理:三角形的稳定性.
被分割的小图形中除了三角形外,不能存在其他多边形.
探究学习
探究四:
尺规作图
作已知角∠AOB的平分线
O
B
A
N
M
C
典例精讲
例3 上述作图得OC平分∠AOB,请说明该做法正确的理由.
O
B
A
N
M
C
解:如图,连结MC、NC .
由作图方法可知:OM = ON,MC = NC,
∴在△OCM和△OCN中,
∴△OCM≌△OCN (SSS),
∴∠AOC =∠BOC (全等三角形的对应角相等),
即OC平分∠AOB.
OM = ON (已知)
MC = NC (已知) ,
OC = OC (公共边)
随堂练习
1. 如图,D、F是线段BC上的两点,AB
=CE,AF=DE,要使△ABF≌△ECD ,还需要条件 .
BF=DC
或 BD=FC
2. 如图,AB=ED,AC=EC,C是BD的中点,若∠A=36°,则∠E= .
【解析】∵C是BD的中点,∴BC=DC.
根据“SSS”说明△ABC≌△EDC,所以∠E=∠A=36°.
36°
A
E
B D F C
A
E
B
C
D
随堂练习
3. 如图,工人师傅砌门时,常用木条 EF 和 EG 来固定门框ABCD,使其不变形,这种做法的根据是( )
A. 两点之间线段最短
B. 长方形的对称性
C. 长方形的四个角都是直角
D. 三角形的稳定性
D
随堂练习
4. 如图,△ABC,用尺规作图作∠ ACB 平分线CD. (保留作图痕迹,不要求写作法)
A
B
C
M
N
D
O
随堂练习
5. 已知: 如图,AC=AD ,BC=BD. 求证: ∠C=∠D.
解:连结AB.
在△ACB 和 △ADB中,
∴△ACB≌△ADB
(SSS),
A
B
C
D
∴∠C=∠D
(全等三角形对应角相等).
AC = AD
BC = BD ,
AB = AB (公共边)
课堂小结
三角形全等的判定
1. 只给出一个或两个条件时,不能保证
两个三角形一定全等.
2. 三边对应相等的两个三角形全等,简
写为“边边边” 或“SSS”.
三角形的稳定性
尺规作图:作已知角的平分线
感谢观看!
第一章 三角形的初步认识
1.5 全等三角形的判定
第1课时 “边边边”
学习目标
探索并理解“边边边”判定方法,会用“边边边”判定方法证明三角形全等;
了解三角形的稳定性及其应用;
会用尺规作已知角的角平分线,了解作图的道理.
温故知新
1. 全等三角形有什么性质?
全等三角形的对应边相等,对应角相等.
2. 已知△ABC≌△DEF,试找出其中相等的边与角.
∠A =∠D
AB =DE
∠B =∠E
BC =EF
∠C =∠F
AC =DF
思考:满足这六个条件可以保证△ABC≌△A′B′C′吗?
A
B
C
D
E
F
探究学习
1.只给一个条件:
①只给一条边:
探究一:
思考:如果只满足这些条件中的一部分,能保证△ABC ≌△DEF 吗
②只给一个角:
1.只给一个条件:
60°
60°
60°
探究一:
结论:
只有一条边或一个角对应相等的两个三角形不一定全等.
2.给出两个条件:
①一条边一个内角:
30°
30°
30°
探究一:
结论:
一条边一个内角对应相等的两个三角形不一定全等.
2.给出两个条件:
探究一:
②两个内角:
30°
50°
结论:
两个内角对应相等的两个三角形不一定全等.
50°
30°
第三个内角一定相等,即三个内角对应相等时,两个三角形不一定全等.
2.给出两个条件:
探究一:
②两条边:
结论:
两条边对应相等的两个三角形不一定全等.
2 cm
4 cm
2 cm
4 cm
结论:只给出一个或两个条件时,
不能保证两个三角形一定全等.
一边一角
一边
总结归纳
一个条件
一角
两个条件
两角
两边
① 三个角;
② 三条边;
③ 两条边一个内角;
④ 两个内角一条边.
两个条件的探究中,已发现不能保证三角形全等.
① 三个角;
交流讨论:
如果满足三个条件,你能说出有哪几种可能的情况?
先任意画出一个△ABC,再画出一个△A′B′C′ ,使A′B′=
AB,B′C′=BC,A′C′=AC. 把画好的△A′B′C′剪下,放到△ABC上,它们全等吗?
A
B
C
探究二:
画法:
1.画线段 B′C′=BC;
2.分别以 B′ 、C′为圆心,BA、
BC为半径画弧,两弧交于点A′;
3. 连接线段 A′B′, A′C′,得到△A′B′C′.
B′
C′
A′
先任意画出一个△ABC,再画出一个△A′B′C′ ,使A′B′=
AB,B′C′=BC,A′C′=AC. 把画好的△A′B′C′剪下,放到△ABC上,它们全等吗?
把画好的△A′B′C′剪下,放到△ABC上.
两个三角形完全重合,说明△ABC 与△A′B′C′全等.
A
B
C
B′
A′
C′
探究二:
三边对应相等的两个三角形全等,
简写为“边边边”或“SSS”.
注:这说明只要三角形三边的长度确定了,这个三角形的形状和大小就完全确定了.此定理也是三角形具有稳定性的原理.
边边边(SSS)
例1 如图:AB=AC,AE=AD,BD=CE,说明△AEB≌△ADC.
C
A
B
D
E
解: ∵BD=CE,
∴BD-ED=CE-ED,即BE=CD.
BE=CD
AB=AC (已知) , AE=AD (已知)
分析:两个三角形中已知两组对应边相等,只需要再说明第三组对应边相等即可.
在△AEB和△ADC中,
∴△AEB≌△ADC (SSS).
典例精讲
探究学习
多边形不稳定
三角形具有稳定性
探究三:
你能举例说明三角形的稳定性在实际生活中的应用吗?
性质应用
典例精讲
例2 要使下列木架不变形各至少需要多少根木条
1根
2根
3根
将多边形变成稳定图形的原理:三角形的稳定性.
被分割的小图形中除了三角形外,不能存在其他多边形.
探究学习
探究四:
尺规作图
作已知角∠AOB的平分线
O
B
A
N
M
C
典例精讲
例3 上述作图得OC平分∠AOB,请说明该做法正确的理由.
O
B
A
N
M
C
解:如图,连结MC、NC .
由作图方法可知:OM = ON,MC = NC,
∴在△OCM和△OCN中,
∴△OCM≌△OCN (SSS),
∴∠AOC =∠BOC (全等三角形的对应角相等),
即OC平分∠AOB.
OM = ON (已知)
MC = NC (已知) ,
OC = OC (公共边)
随堂练习
1. 如图,D、F是线段BC上的两点,AB
=CE,AF=DE,要使△ABF≌△ECD ,还需要条件 .
BF=DC
或 BD=FC
2. 如图,AB=ED,AC=EC,C是BD的中点,若∠A=36°,则∠E= .
【解析】∵C是BD的中点,∴BC=DC.
根据“SSS”说明△ABC≌△EDC,所以∠E=∠A=36°.
36°
A
E
B D F C
A
E
B
C
D
随堂练习
3. 如图,工人师傅砌门时,常用木条 EF 和 EG 来固定门框ABCD,使其不变形,这种做法的根据是( )
A. 两点之间线段最短
B. 长方形的对称性
C. 长方形的四个角都是直角
D. 三角形的稳定性
D
随堂练习
4. 如图,△ABC,用尺规作图作∠ ACB 平分线CD. (保留作图痕迹,不要求写作法)
A
B
C
M
N
D
O
随堂练习
5. 已知: 如图,AC=AD ,BC=BD. 求证: ∠C=∠D.
解:连结AB.
在△ACB 和 △ADB中,
∴△ACB≌△ADB
(SSS),
A
B
C
D
∴∠C=∠D
(全等三角形对应角相等).
AC = AD
BC = BD ,
AB = AB (公共边)
课堂小结
三角形全等的判定
1. 只给出一个或两个条件时,不能保证
两个三角形一定全等.
2. 三边对应相等的两个三角形全等,简
写为“边边边” 或“SSS”.
三角形的稳定性
尺规作图:作已知角的平分线
感谢观看!
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
