圆的基本性质复习(浙江省杭州市)

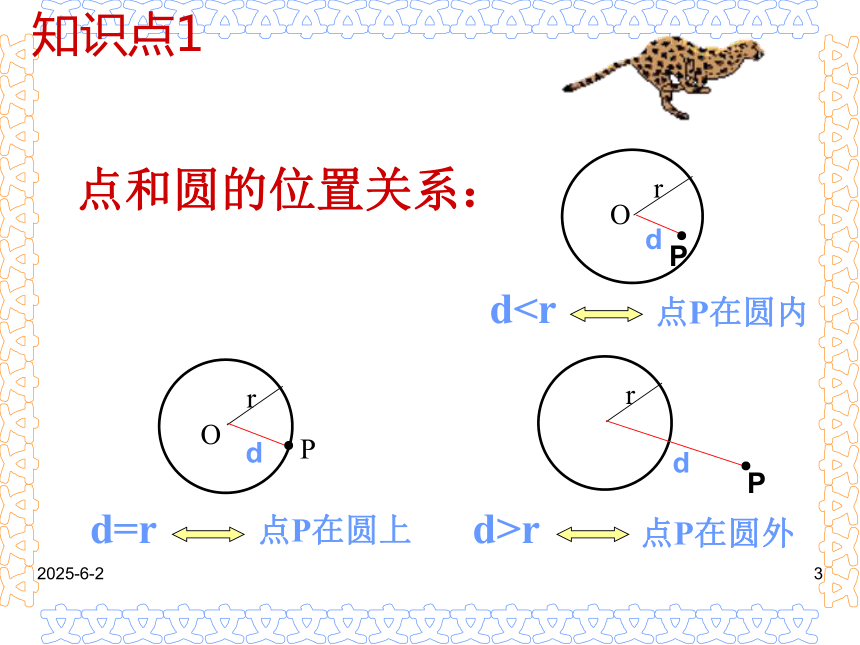
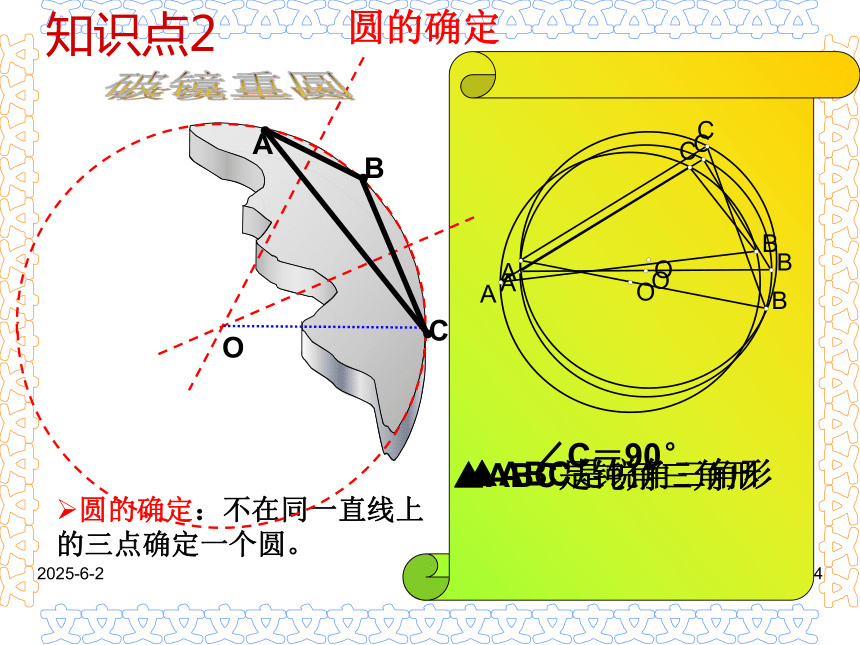
课件22张PPT。2019-3-141复习课题:圆的基本性质复习2019-3-1412019-3-141点和圆的位置关系：知识点12019-3-141圆的确定：不在同一直线上的三点确定一个圆。圆的确定O破镜重圆知识点22019-3-141仔细辩一辩判断：
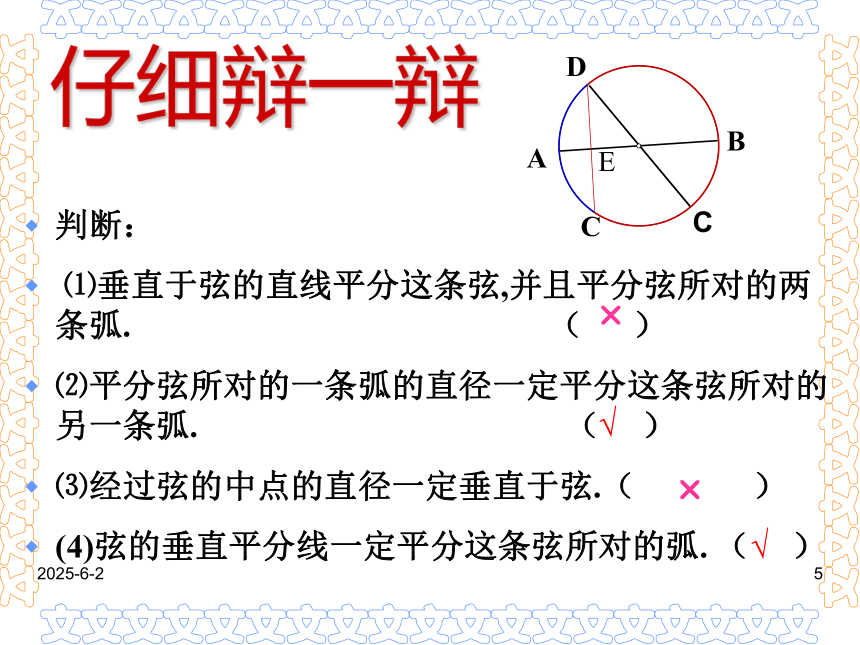
⑴垂直于弦的直线平分这条弦,并且平分弦所对的两条弧. （ ）
⑵平分弦所对的一条弧的直径一定平分这条弦所对的另一条弧. （ ）
⑶经过弦的中点的直径一定垂直于弦.（ ）
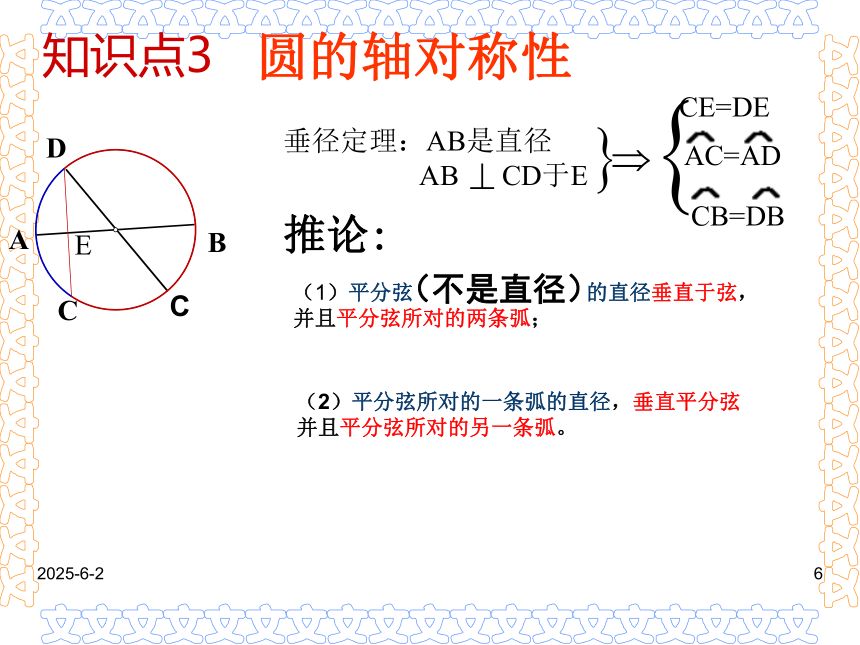
(4)弦的垂直平分线一定平分这条弦所对的弧. （ ）√??√EDAB2019-3-141圆的轴对称性EDBA垂径定理：AB是直径
AB CD于E推论:
知识点3

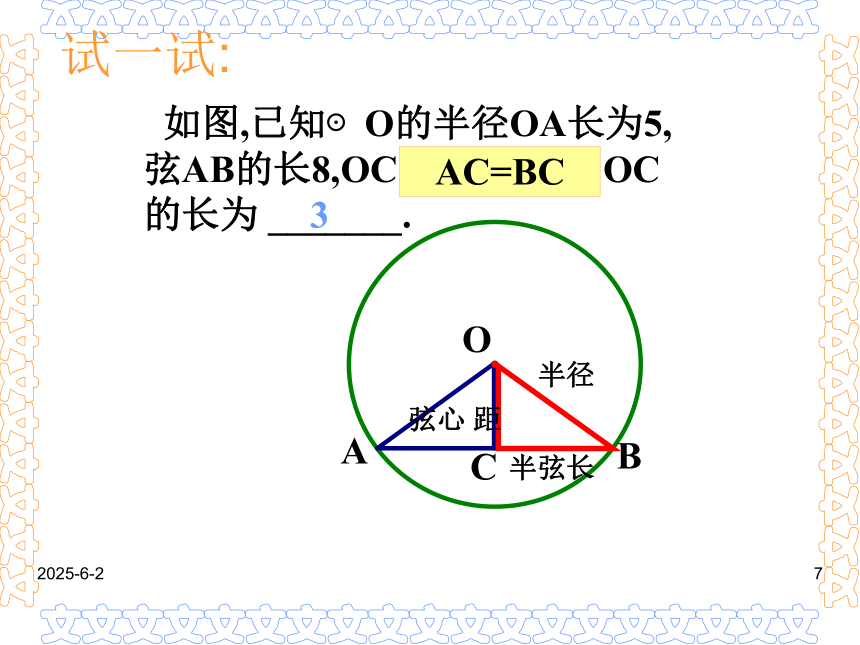
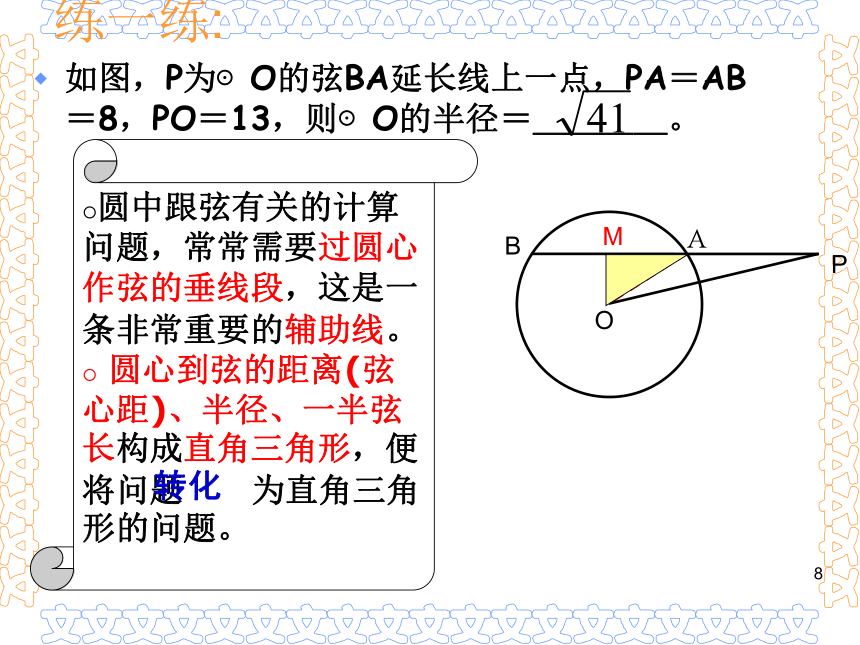
（2）平分弦所对的一条弧的直径，垂直平分弦并且平分弦所对的另一条弧。（1）平分弦 的直径垂直于弦，并且平分弦所对的两条弧；（不是直径）2019-3-141 如图,已知⊙O的半径OA长为5,弦AB的长8,OC⊥AB于C,则OC的长为 _______.3AC=BC试一试:2019-3-141如图，P为⊙O的弦BA延长线上一点，PA＝AB＝8，PO＝13，则⊙O的半径＝＿＿＿＿。圆中跟弦有关的计算问题，常常需要过圆心作弦的垂线段，这是一条非常重要的辅助线。
圆心到弦的距离(弦心距)、半径、一半弦长构成直角三角形，便将问题 为直角三角形的问题。Ａ练一练:转化2019-3-141圆心角、弧、弦、弦心距之间的关系圆的旋转不变性知识点42019-3-141如图,在同圆中,OC⊥AB于C,OC`⊥A`B`于C` 。∵ ，
∴ AB = A`B`
（填写一个条件．你有几种填法？你的根据是什么？） 　　　　　
如果两个圆心角、两条弧、
两条弦或两条弦的弦心距中有
一组量相等，那么它们所对应
的其余各组量都分别相等。在同圆或等圆中：2019-3-141⑴圆周角 与圆心角如图：
⑴ 如果∠AOB=100°，则∠C= 。ABCO⑵ 当∠C= 时，A、O、B三点在同一直线上。　　　　　圆周角定理 一条弧所对的圆周角等于它所对的圆心角的一半。　　　　　推论：半圆（或直径）所对的圆周角是直角；90°的圆周角所对弦是直径。 50°90°知识点52019-3-141⌒⌒120°125°练一练：2019-3-141如图，比较∠C、∠D、∠E的大小
同弧所对的圆周角相等如图，如果弧AB＝弧CD，那么∠E和∠F是什么关系？反过来呢？
等弧所对的圆周角相等；在同圆中，相等的圆周角所对的弧也相等如图，⊙O1和⊙O2是等圆，如果弧AB＝弧CD，那么∠E和∠F是什么关系？反过来呢？等圆也成立⑵圆周角与弧2019-3-141例: 如图， ⊙O 中，弦AB=CD，AB 与CD交于点M，BCADMO2019-3-141∠AOB=______ 度， 已知：如图，△ABC内接于⊙O ，点A、B、C把⊙O三等分，则 弧AB=______ 度 ，∠ ACB=______ 度第(5)题注意: 弧的度数和角的度数的相互转化120°120°60°2019-3-1411、如图，弦AB、CD相交于点E，若AC为80 ° ，BD为40 ° ，则∠ AEC=________度⌒⌒2、如图，E为圆外的一点，EA交圆于点B，EC交圆于点D，若AC为80 ° BD为40° ，则
∠ AEC=________度⌒⌒6020弧的度数和角的度数的转化圆周角或圆心角2019-3-141 回顾与小结(1): 我们复习了圆的哪些基本性质?(2): 在应用这些基本性质时,你觉得哪些 地方容易犯错误?大家说一说,评一评2019-3-141检测反馈:请同学们准备好测试卷，
限时7分钟完成，
比一比哪个组的同学速度最快，
效率最高！2019-3-141CC∟E2019-3-141直径PQ⊥弦CD证明:直径PQ⊥弦ABAE=BE∵∴∴∴∴∵即或连AD,∵∴∴∵直径PQ⊥弦CD∴直径PQ⊥弦AB∴AE=BE2019-3-141
OABCEFD应用提高:2019-3-141感谢同学们的参与