4.1 比例线段 (2) 课件(共23张PPT)
文档属性
| 名称 | 4.1 比例线段 (2) 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-11 00:00:00 | ||
图片预览



文档简介
(共23张PPT)
浙教版九年级上册
4.1 比例线段 (2)
第四章 相似三角形
AB=
.
=
.
A1B1=
.
=
.
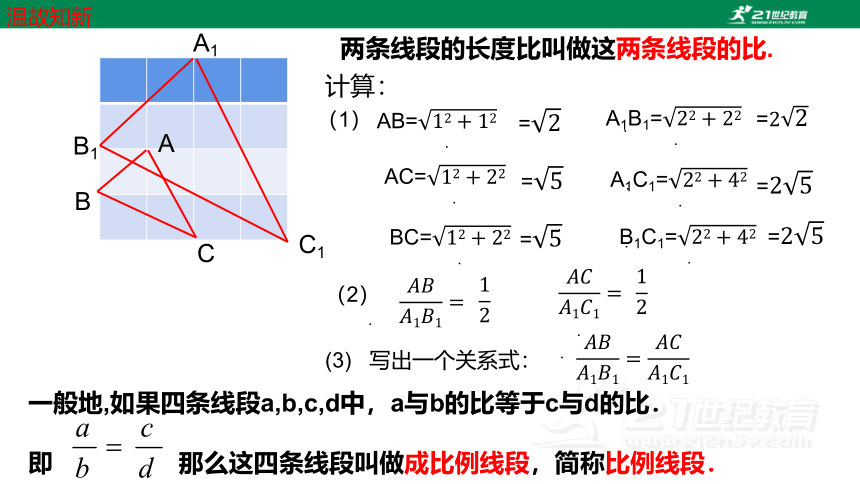
计算:
AC=
.
=
.
A1C1=
.
=
.
BC=
.
=
.
B1C1=
.
=
.
.
(1)
(2)
两条线段的长度比叫做这两条线段的比.
(3) 写出一个关系式:
一般地,如果四条线段a,b,c,d中,a与b的比等于c与d的比.
即 那么这四条线段叫做成比例线段,简称比例线段.
A
B
C
A1
B1
C1
温故知新
.
.
C′
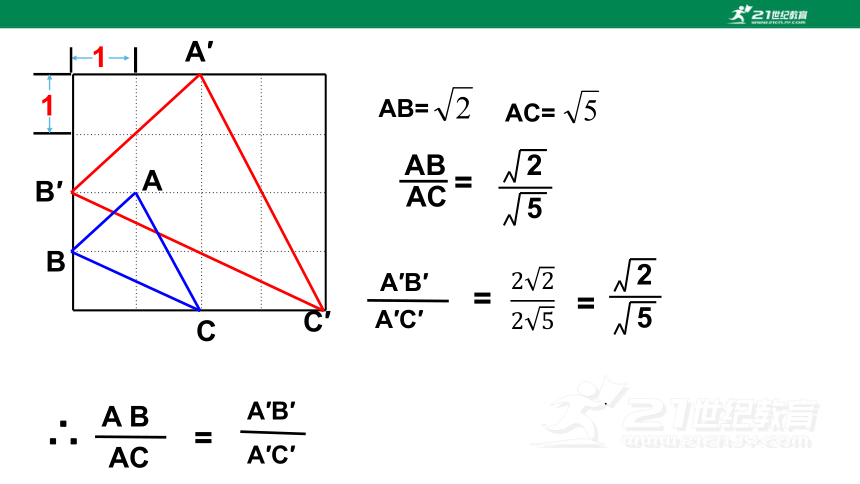
AB
AC
=
5
2
A′B′
=
A′C′
∴
A B
A′B′
=
AC
A′C′
A
B
C
A′
B′
1
1
AB=
AC=
5
2
=
.
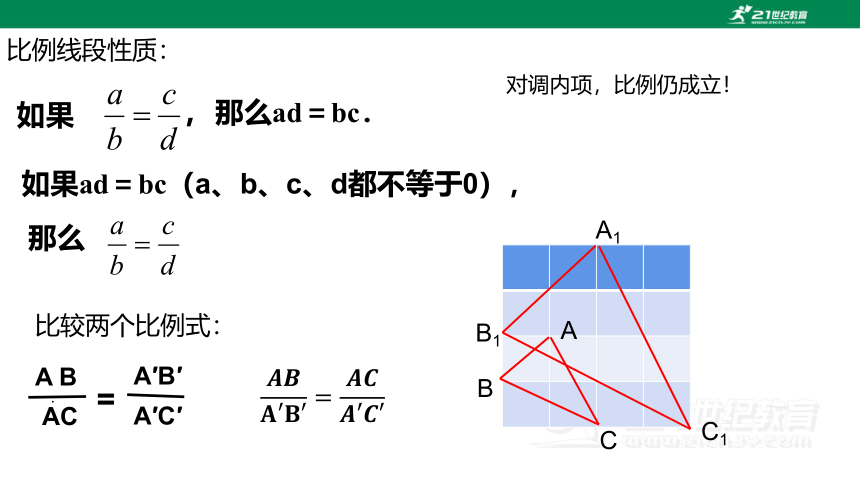
如果
,那么ad=bc.
比例线段性质:
如果ad=bc(a、b、c、d都不等于0),
那么
A
B
C
A1
B1
C1
.
A B
A′B′
=
AC
A′C′
比较两个比例式:
对调内项,比例仍成立!
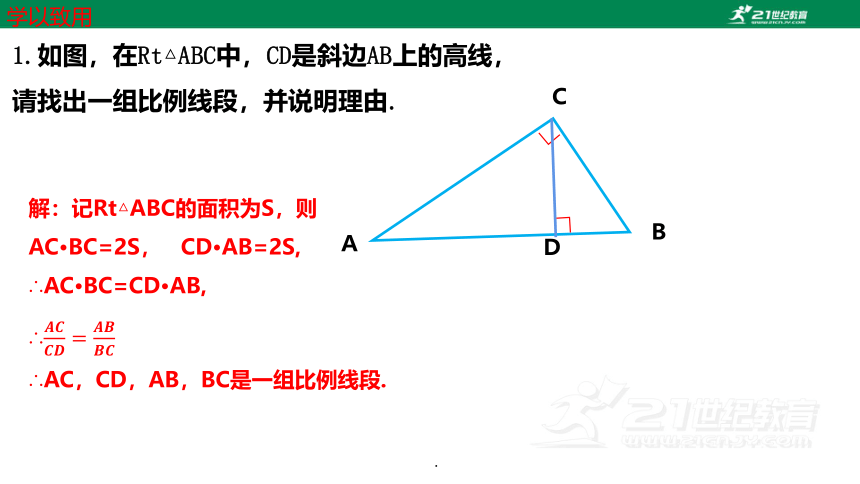
1.如图,在Rt△ABC中,CD是斜边AB上的高线,
请找出一组比例线段,并说明理由.
∟
∟
A
B
C
D
学以致用
解:记Rt△ABC的面积为S,则
AC·BC=2S, CD·AB=2S,
∴AC·BC=CD·AB,
∴
∴AC,CD,AB,BC是一组比例线段.
.
2.如图,已知AD,CE是△ABC中BC、AB上的高线,
求证:AD:CE=AB:BC
┛
┛
解:记△ABC的面积为S,则
BC·AD=2S,AB·CE=2S,
∴BC·AD=AB·CE,
∴,AD:CE=AB:BC
∴AC,CD,AB,BC是一组比例线段.
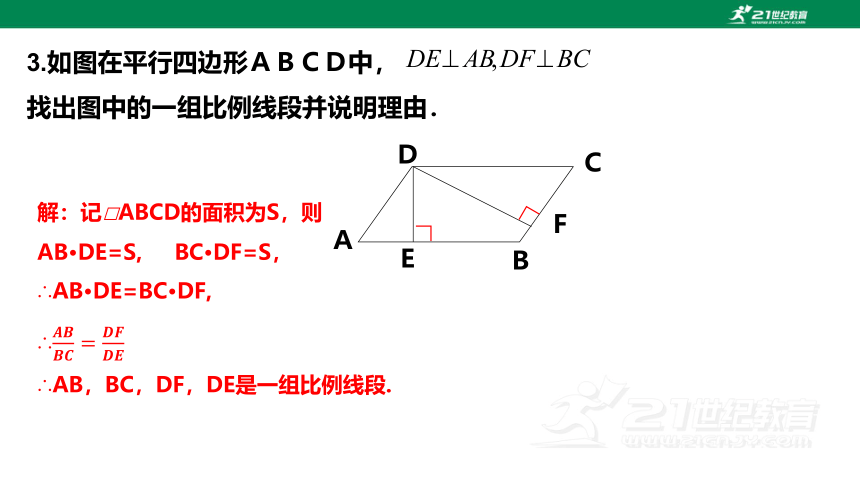
3.如图在平行四边形ABCD中,
找出图中的一组比例线段并说明理由.
F
E
D
C
B
A
∟
∟
解:记□ABCD的面积为S,则
AB·DE=S, BC·DF=S,
∴AB·DE=BC·DF,
∴
∴AB,BC,DF,DE是一组比例线段.
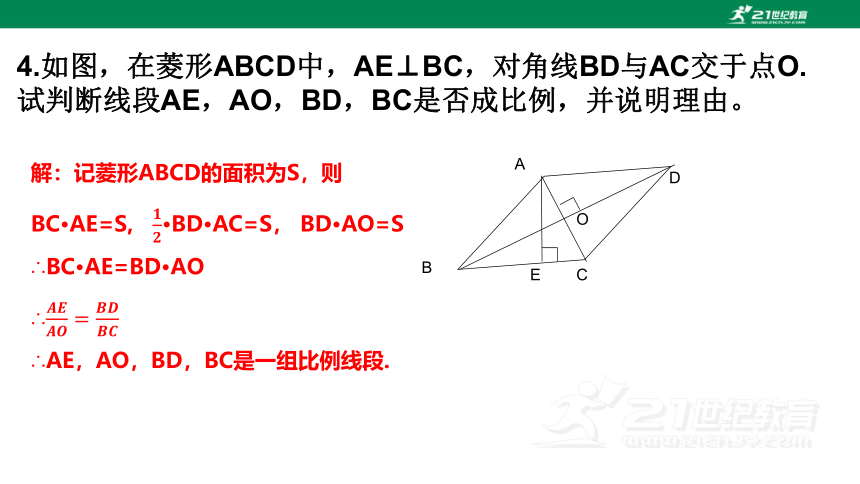
4.如图,在菱形ABCD中,AE⊥BC,对角线BD与AC交于点O.试判断线段AE,AO,BD,BC是否成比例,并说明理由。
A
B
C
D
O
E
解:记菱形ABCD的面积为S,则
BC·AE=S, ·BD·AC=S, BD·AO=S
∴BC·AE=BD·AO
∴
∴AE,AO,BD,BC是一组比例线段.
5、如图,是我国台湾省的几个城市的位置图,问基隆市在高雄市的哪一个方向?到高雄市的实际距离是多少km?(比例尺1:9000000)
解:从图上量出高雄市到基隆市的距离约35mm,设实际距离为s,则
35
s
=
1
9000000
∴S=35×9000000=315000000(mm)
即s=315(km)
如果量得图中,我们还能确定基隆市在高雄市的北偏东28的315km处.
A
B
C
AB=2
.
.
AC=
.
=
.
=
.
BC=
.
=
.
.
=
.
=
.
.
.
.
.
.
.
1.计算:
夯实基础,稳扎稳打
.
.
.
2.在比例尺1:10000的地图上,相距2cm的A、B两地,
它们的实际距离为多少
米?
.
x=2×10000
x=20000 (cm)
=200 (m)
A
B
C
┛
450
A1
B1
C1
┛
450
4.配套数字
1: 1 :
.
请写出几组比例线段
.
.
.
.
.
A
B
C
┛
300
A1
B1
C1
┛
300
5.配套数字
1: :2
.
请写出几组比例线段
.
.
.
.
.
6.配套数字
1:1 :
.
请写出几组比例线段
.
.
.
.
.
A1
B1
C1
300
300
1200
A
B
C
300
300
1200
A
连续递推,豁然开朗
8.如图,DE是△ABC的中位线.请尽可能多地写出比例线段.
对每一组比例线段,写出一个比例式(至少要写出两组).
A
B
C
D
E
┛
B
A
思维拓展,更上一层
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
浙教版九年级上册
4.1 比例线段 (2)
第四章 相似三角形
AB=
.
=
.
A1B1=
.
=
.
计算:
AC=
.
=
.
A1C1=
.
=
.
BC=
.
=
.
B1C1=
.
=
.
.
(1)
(2)
两条线段的长度比叫做这两条线段的比.
(3) 写出一个关系式:
一般地,如果四条线段a,b,c,d中,a与b的比等于c与d的比.
即 那么这四条线段叫做成比例线段,简称比例线段.
A
B
C
A1
B1
C1
温故知新
.
.
C′
AB
AC
=
5
2
A′B′
=
A′C′
∴
A B
A′B′
=
AC
A′C′
A
B
C
A′
B′
1
1
AB=
AC=
5
2
=
.
如果
,那么ad=bc.
比例线段性质:
如果ad=bc(a、b、c、d都不等于0),
那么
A
B
C
A1
B1
C1
.
A B
A′B′
=
AC
A′C′
比较两个比例式:
对调内项,比例仍成立!
1.如图,在Rt△ABC中,CD是斜边AB上的高线,
请找出一组比例线段,并说明理由.
∟
∟
A
B
C
D
学以致用
解:记Rt△ABC的面积为S,则
AC·BC=2S, CD·AB=2S,
∴AC·BC=CD·AB,
∴
∴AC,CD,AB,BC是一组比例线段.
.
2.如图,已知AD,CE是△ABC中BC、AB上的高线,
求证:AD:CE=AB:BC
┛
┛
解:记△ABC的面积为S,则
BC·AD=2S,AB·CE=2S,
∴BC·AD=AB·CE,
∴,AD:CE=AB:BC
∴AC,CD,AB,BC是一组比例线段.
3.如图在平行四边形ABCD中,
找出图中的一组比例线段并说明理由.
F
E
D
C
B
A
∟
∟
解:记□ABCD的面积为S,则
AB·DE=S, BC·DF=S,
∴AB·DE=BC·DF,
∴
∴AB,BC,DF,DE是一组比例线段.
4.如图,在菱形ABCD中,AE⊥BC,对角线BD与AC交于点O.试判断线段AE,AO,BD,BC是否成比例,并说明理由。
A
B
C
D
O
E
解:记菱形ABCD的面积为S,则
BC·AE=S, ·BD·AC=S, BD·AO=S
∴BC·AE=BD·AO
∴
∴AE,AO,BD,BC是一组比例线段.
5、如图,是我国台湾省的几个城市的位置图,问基隆市在高雄市的哪一个方向?到高雄市的实际距离是多少km?(比例尺1:9000000)
解:从图上量出高雄市到基隆市的距离约35mm,设实际距离为s,则
35
s
=
1
9000000
∴S=35×9000000=315000000(mm)
即s=315(km)
如果量得图中,我们还能确定基隆市在高雄市的北偏东28的315km处.
A
B
C
AB=2
.
.
AC=
.
=
.
=
.
BC=
.
=
.
.
=
.
=
.
.
.
.
.
.
.
1.计算:
夯实基础,稳扎稳打
.
.
.
2.在比例尺1:10000的地图上,相距2cm的A、B两地,
它们的实际距离为多少
米?
.
x=2×10000
x=20000 (cm)
=200 (m)
A
B
C
┛
450
A1
B1
C1
┛
450
4.配套数字
1: 1 :
.
请写出几组比例线段
.
.
.
.
.
A
B
C
┛
300
A1
B1
C1
┛
300
5.配套数字
1: :2
.
请写出几组比例线段
.
.
.
.
.
6.配套数字
1:1 :
.
请写出几组比例线段
.
.
.
.
.
A1
B1
C1
300
300
1200
A
B
C
300
300
1200
A
连续递推,豁然开朗
8.如图,DE是△ABC的中位线.请尽可能多地写出比例线段.
对每一组比例线段,写出一个比例式(至少要写出两组).
A
B
C
D
E
┛
B
A
思维拓展,更上一层
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
