2.4 等腰三角形的判定定理 课件(18张PPT)
文档属性
| 名称 | 2.4 等腰三角形的判定定理 课件(18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 456.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 08:47:19 | ||
图片预览


文档简介
(共18张PPT)
等腰三角形的判定
等腰三角形的判定
浙教版 八上
目录
目录
等角对等边
01
等边三角形的判定1
03
判定和性质的关系
02
等边三角形的判定2
04
直观感知——操作确认——推理论证
情境导入
在△ABC中,AB=AC,倘若不留神,它的一部分被墨水涂没了,只留下一条底边BC和一个底角∠C, 有没有办法把原来的等腰三角形画出来?
B
C
导入新知
如图所示,量出AC的长,就可算出河的宽度AB,你知道为什么吗?
A
B
C
60°
30°
建立数学模型
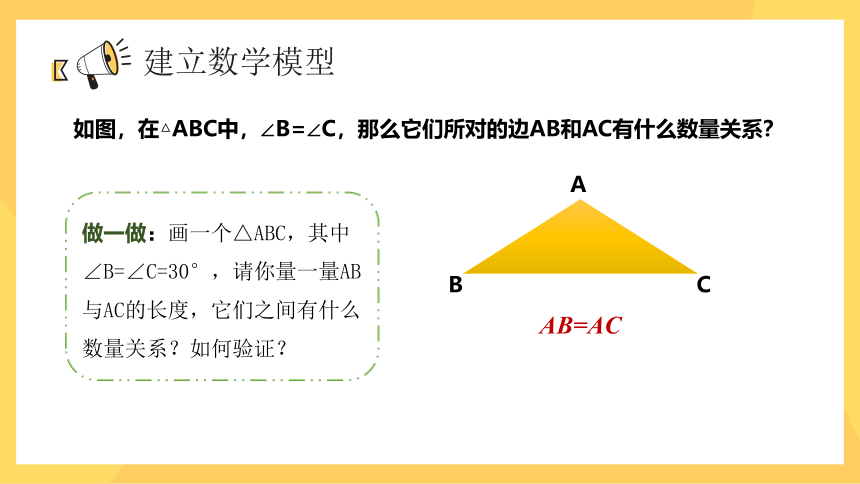
如图,在△ABC中,∠B=∠C,那么它们所对的边AB和AC有什么数量关系?
B
C
A
做一做:画一个△ABC,其中∠B=∠C=30°,请你量一量AB与AC的长度,它们之间有什么数量关系?如何验证?
AB=AC
建立数学模型
B
C
A
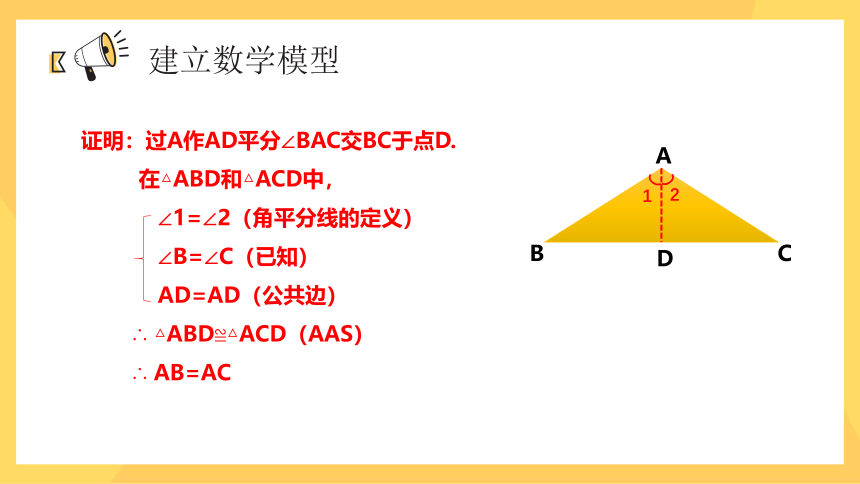
证明:过A作AD平分∠BAC交BC于点D.
在△ABD和△ACD中,
∠1=∠2(角平分线的定义)
∠B=∠C(已知)
AD=AD(公共边)
∴ △ABD≌△ACD(AAS)
∴ AB=AC
D
1
2
知识要点
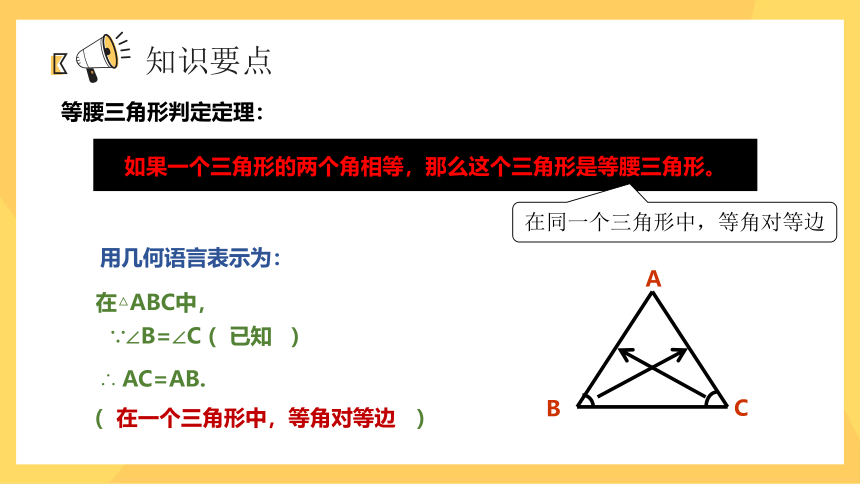
等腰三角形判定定理:
如果一个三角形的两个角相等,那么这个三角形是等腰三角形。
在同一个三角形中,等角对等边
用几何语言表示为:
在△ABC中,
∵∠B=∠C ( 已知 )
∴ AC=AB. ( )
在一个三角形中,等角对等边
A
B
C
在同一个三角形中,
等角对等边
问:如图,下列推理正确吗
A
B
C
D
2
1
∵∠1=∠2 ∴ BD=DC
(等角对等边)
∵∠1=∠2 ∴ DC=BC
A
B
C
D
2
1
(等角对等边)
错,因为都不是在同一个三角形中。
例题学习
一次数学实践活动的内容是测量河宽,如图,即测量A,B之间的距离.同学们想出了许多方法,其中小聪的方法是:从点A出发,沿着与直线AB成60°角的AC方向前进至C,在C处测得∠C=30°.量出AC的长,它就是河的宽度AB(即A,B之间的距离).这个方法正确吗?请说明理由.
解:这一方法正确。理由如下:
∵ ∠CAD=∠B+∠C(三角形的外角等于与它不相邻的两个内角的和)
∴ ∠B=∠CAD-∠C=60°-30°=30°
∴ ∠B=∠C
∴ AB=AC(在同一个三角形中,等角对等边)
归纳小结
名称 图形 性质 判定 注意事项
等腰三角形
2.等边对等角
3. 三线合一
4.是轴对称图形
2.等角对等边
1.两边相等
1.两腰相等
这是根据等腰三角形的定义进行判断的
通过计算三角形各角的度数也可得到角相等.在运用时要找准“边”与“角”
归纳小结
三个角都相等的三角形是等边三角形
证明:∵∠A=∠B=∠C=60°
∴AB=AC=BC
∴△ABC是等边三角形
A
B
C
三条边都相等的三角形是等边三角形
等边三角形的判定定理1:
等边三角形的定义:
归纳小结
等边三角形的判定定理2:
有一个角是60°的三角形是等边三角形
点拨:
有一个角是60°,在等腰三角形中有两种情况:(1)这个角是底角;(2)这个角是顶角.
A
C
B
60°
证明: ∵AB=AC,∠B=60°(已知),
∴∠C=∠B=60°(在同一个三角形中,等角对等边)
∴∠A=60°(三角形内角和定理).
∴∠A=∠B =∠C=60°.
∴△ABC是等边三角形(三个角都相等的三角形是等边三角形)
第一种情况:有一个底角是60°;
归纳小结
第二种情况:有一个顶角是60°;
证明:∵AB=AC,∠A=60°(已知),
∴∠C=∠B=60°(在同一个三角形中,等角对等边)
∴∠A=∠B=∠C =60°,
∴△ABC是等边三角形(三个角都相等的三角形是等边三角形).
A
C
B
60°
练一练
A
B
C
D
E
1
2
如图,已知DE∥BC,∠1=∠2. 求证:△ABC 是等腰三角形.
证明:
∵ ∠1=∠2(已知)
∴ AD=AE(在同一个三角形中,等角对等边)
∵ DE∥BC(已知)
∴ ∠1=∠B,∠2=∠C
∴ ∠B=∠C
∴ AB=AC(在同一个三角形中,等角对等边)
∴ AB-AD=AE-AC
即 BD=CE
举一反三
1. 如图,上午8时,一艘船从A处出发以15海里/时的速度向正北方向航行,9时45分到达B处. 从A处测得灯塔C在北偏西26°方向, 从B处测得灯塔C在北偏西52°方向, 求B处到灯塔C的距离.
A
B
C
E
北
26°
52°
解:∵∠A=26° ∠C=52°-26°=26°
∴∠A=∠C
∴△ABC是一个等腰三角形
∴AB=BC
AB=15×1.75=25.85海里
举一反三
2. 如图,AD平分△ABC的外角∠EAC,AD//BC,则△ ABC是等腰三角形吗?证明你的判断。
A
E
B
C
1
2
D
证明:∵AD∥BC,
∴∠1=∠B(两直线平行,同位角相等)
∠2=∠C(两直线平行,内错角相等)
∵ ∠1=∠2,
∴ ∠B=∠C
∴ AB=AC(等角对等边)
举一反三
在△ABC中,已知 AB =AC ,BO平分∠ABC,CO平分∠ACB
③猜想线段DE和线段DB,EC之间的关系 并说明理由。
B
O
C
A
D
E
DE=DB+CE
②过点O作DE∥BC,则图中有 个等腰三角形。
①则△OBC是 三角形
等腰
5
∵BO平分∠ABC, CO平分∠ACB
∴∠DBO=∠CBO,∠ECO=∠OCB
∵DE∥BC
∴∠DOB=∠CBO,∠EOC=∠OCB
∴∠DOB=∠DBO,∠EOC=∠ECO
∴DB=DO,EC=EO
∵DE=DO+EO
∴DE=DB+CE
请多指教
请多指教
谢谢
等腰三角形的判定
等腰三角形的判定
浙教版 八上
目录
目录
等角对等边
01
等边三角形的判定1
03
判定和性质的关系
02
等边三角形的判定2
04
直观感知——操作确认——推理论证
情境导入
在△ABC中,AB=AC,倘若不留神,它的一部分被墨水涂没了,只留下一条底边BC和一个底角∠C, 有没有办法把原来的等腰三角形画出来?
B
C
导入新知
如图所示,量出AC的长,就可算出河的宽度AB,你知道为什么吗?
A
B
C
60°
30°
建立数学模型
如图,在△ABC中,∠B=∠C,那么它们所对的边AB和AC有什么数量关系?
B
C
A
做一做:画一个△ABC,其中∠B=∠C=30°,请你量一量AB与AC的长度,它们之间有什么数量关系?如何验证?
AB=AC
建立数学模型
B
C
A
证明:过A作AD平分∠BAC交BC于点D.
在△ABD和△ACD中,
∠1=∠2(角平分线的定义)
∠B=∠C(已知)
AD=AD(公共边)
∴ △ABD≌△ACD(AAS)
∴ AB=AC
D
1
2
知识要点
等腰三角形判定定理:
如果一个三角形的两个角相等,那么这个三角形是等腰三角形。
在同一个三角形中,等角对等边
用几何语言表示为:
在△ABC中,
∵∠B=∠C ( 已知 )
∴ AC=AB. ( )
在一个三角形中,等角对等边
A
B
C
在同一个三角形中,
等角对等边
问:如图,下列推理正确吗
A
B
C
D
2
1
∵∠1=∠2 ∴ BD=DC
(等角对等边)
∵∠1=∠2 ∴ DC=BC
A
B
C
D
2
1
(等角对等边)
错,因为都不是在同一个三角形中。
例题学习
一次数学实践活动的内容是测量河宽,如图,即测量A,B之间的距离.同学们想出了许多方法,其中小聪的方法是:从点A出发,沿着与直线AB成60°角的AC方向前进至C,在C处测得∠C=30°.量出AC的长,它就是河的宽度AB(即A,B之间的距离).这个方法正确吗?请说明理由.
解:这一方法正确。理由如下:
∵ ∠CAD=∠B+∠C(三角形的外角等于与它不相邻的两个内角的和)
∴ ∠B=∠CAD-∠C=60°-30°=30°
∴ ∠B=∠C
∴ AB=AC(在同一个三角形中,等角对等边)
归纳小结
名称 图形 性质 判定 注意事项
等腰三角形
2.等边对等角
3. 三线合一
4.是轴对称图形
2.等角对等边
1.两边相等
1.两腰相等
这是根据等腰三角形的定义进行判断的
通过计算三角形各角的度数也可得到角相等.在运用时要找准“边”与“角”
归纳小结
三个角都相等的三角形是等边三角形
证明:∵∠A=∠B=∠C=60°
∴AB=AC=BC
∴△ABC是等边三角形
A
B
C
三条边都相等的三角形是等边三角形
等边三角形的判定定理1:
等边三角形的定义:
归纳小结
等边三角形的判定定理2:
有一个角是60°的三角形是等边三角形
点拨:
有一个角是60°,在等腰三角形中有两种情况:(1)这个角是底角;(2)这个角是顶角.
A
C
B
60°
证明: ∵AB=AC,∠B=60°(已知),
∴∠C=∠B=60°(在同一个三角形中,等角对等边)
∴∠A=60°(三角形内角和定理).
∴∠A=∠B =∠C=60°.
∴△ABC是等边三角形(三个角都相等的三角形是等边三角形)
第一种情况:有一个底角是60°;
归纳小结
第二种情况:有一个顶角是60°;
证明:∵AB=AC,∠A=60°(已知),
∴∠C=∠B=60°(在同一个三角形中,等角对等边)
∴∠A=∠B=∠C =60°,
∴△ABC是等边三角形(三个角都相等的三角形是等边三角形).
A
C
B
60°
练一练
A
B
C
D
E
1
2
如图,已知DE∥BC,∠1=∠2. 求证:△ABC 是等腰三角形.
证明:
∵ ∠1=∠2(已知)
∴ AD=AE(在同一个三角形中,等角对等边)
∵ DE∥BC(已知)
∴ ∠1=∠B,∠2=∠C
∴ ∠B=∠C
∴ AB=AC(在同一个三角形中,等角对等边)
∴ AB-AD=AE-AC
即 BD=CE
举一反三
1. 如图,上午8时,一艘船从A处出发以15海里/时的速度向正北方向航行,9时45分到达B处. 从A处测得灯塔C在北偏西26°方向, 从B处测得灯塔C在北偏西52°方向, 求B处到灯塔C的距离.
A
B
C
E
北
26°
52°
解:∵∠A=26° ∠C=52°-26°=26°
∴∠A=∠C
∴△ABC是一个等腰三角形
∴AB=BC
AB=15×1.75=25.85海里
举一反三
2. 如图,AD平分△ABC的外角∠EAC,AD//BC,则△ ABC是等腰三角形吗?证明你的判断。
A
E
B
C
1
2
D
证明:∵AD∥BC,
∴∠1=∠B(两直线平行,同位角相等)
∠2=∠C(两直线平行,内错角相等)
∵ ∠1=∠2,
∴ ∠B=∠C
∴ AB=AC(等角对等边)
举一反三
在△ABC中,已知 AB =AC ,BO平分∠ABC,CO平分∠ACB
③猜想线段DE和线段DB,EC之间的关系 并说明理由。
B
O
C
A
D
E
DE=DB+CE
②过点O作DE∥BC,则图中有 个等腰三角形。
①则△OBC是 三角形
等腰
5
∵BO平分∠ABC, CO平分∠ACB
∴∠DBO=∠CBO,∠ECO=∠OCB
∵DE∥BC
∴∠DOB=∠CBO,∠EOC=∠OCB
∴∠DOB=∠DBO,∠EOC=∠ECO
∴DB=DO,EC=EO
∵DE=DO+EO
∴DE=DB+CE
请多指教
请多指教
谢谢
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
