一次函数复习(浙江省金华市)

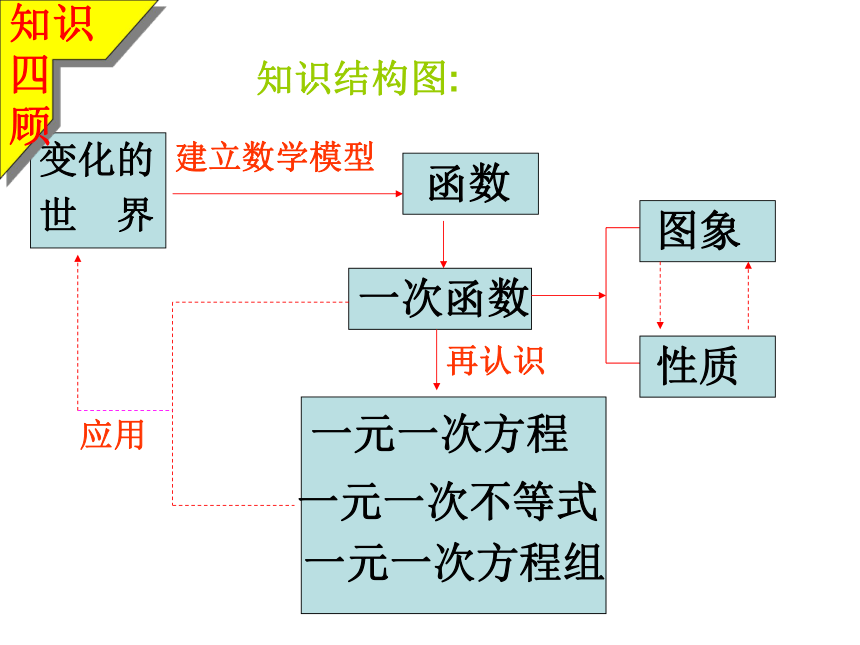
课件25张PPT。妈妈，智慧堡是不是快到了？因为我已经学会了一次函数及其应用呀！为什么你这样认为呢？你会了吗？不就是分三步走吗？可你知道第三步怎么“走”吗？函数Y=KX+b（K，b都是常数,且K≠0)叫做一次函数. x为自变量，y为因变量）．一次函数y=kx+b(k≠0)的图象是一条直线.性质:一次函数y=kx+b(k、b为常数，且k≠0),当k>0时，y随着x的增大而增大；当k<0时，y随着x的增大而减小。知识结构图:变化的
世　界函数一次函数图象性质一元一次方程一元一次不等式一元一次方程组再认识建立数学模型应用知识四
顾八年级 数学第十一章 函数求出下列函数中自变量的取值范围?自变量的取值范围请你理
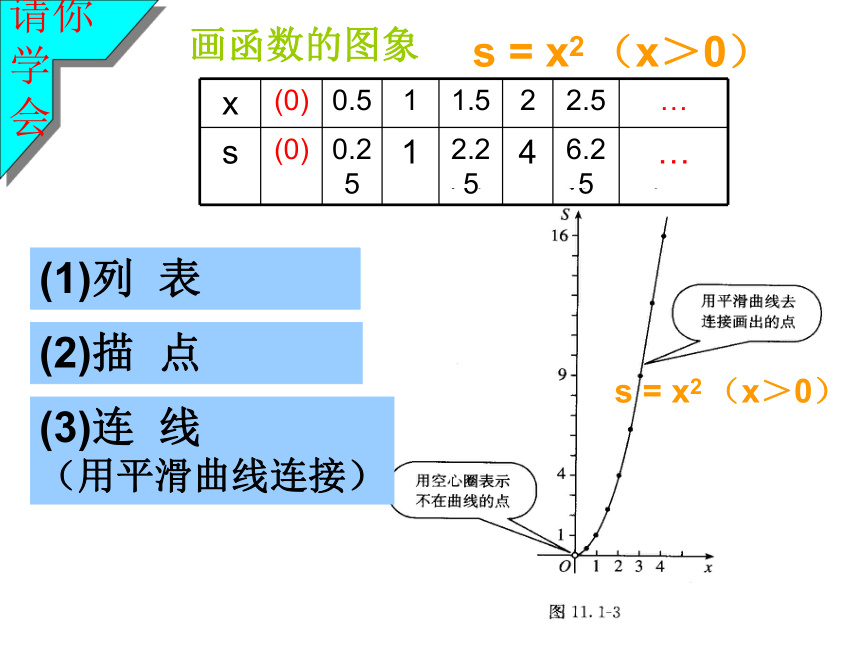
解八年级 数学第十一章 函数 画函数的图象s = x2 （x＞0）s = x2 （x＞0）请你学
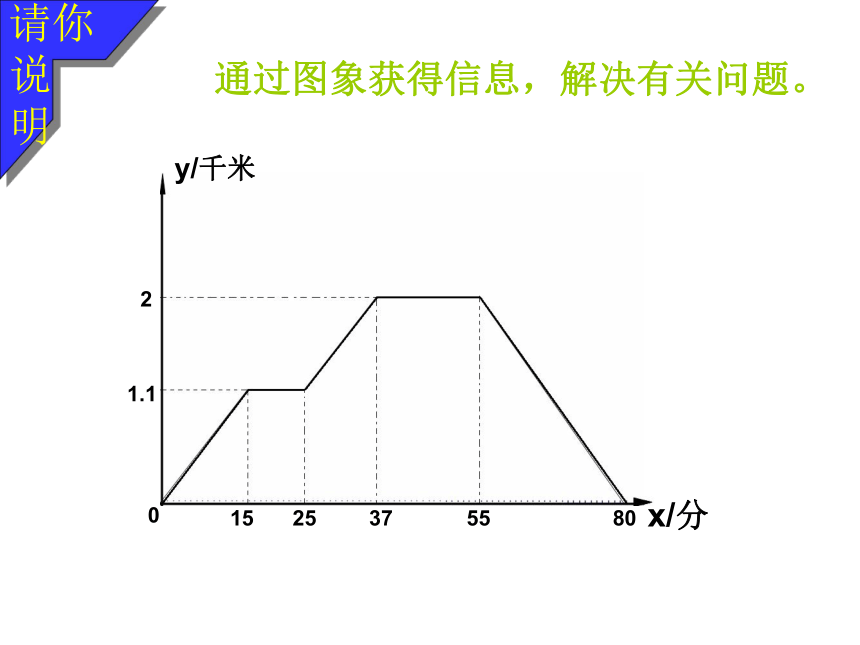
会 通过图象获得信息，解决有关问题。 请你说
明第十一章 函数一次函数的概念：一般地，形如y=kx+b(k,b为常数，且k≠0)
的函数叫做一次函数. 当b =0 时,y=kx+b 即为 y=kx,
所以正比例函数，是一次函数的特例.熟练理
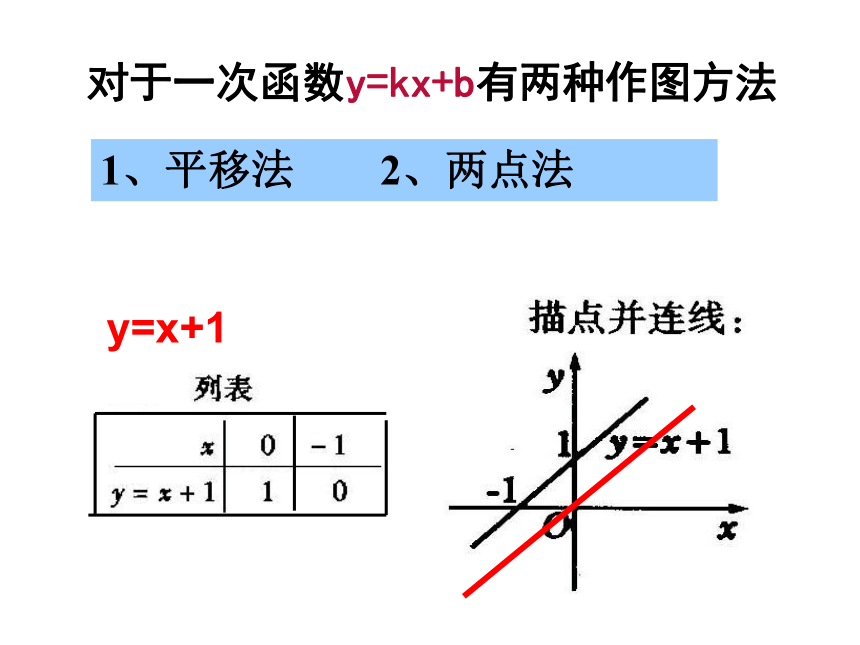
解对于一次函数y=kx+b有两种作图方法1、平移法 2、两点法y=x+1一次函数的图象与性质:一次函数y=kx+b的图象是一条直线,
k>0, y随x的增大而增大;
k<0 ,y随x的增大而减小.注意：k,b决定图象所经过的象限.
k决定上升与下降
b决定图象与y轴的交点位置. 与y轴的交点为 (0 , b )
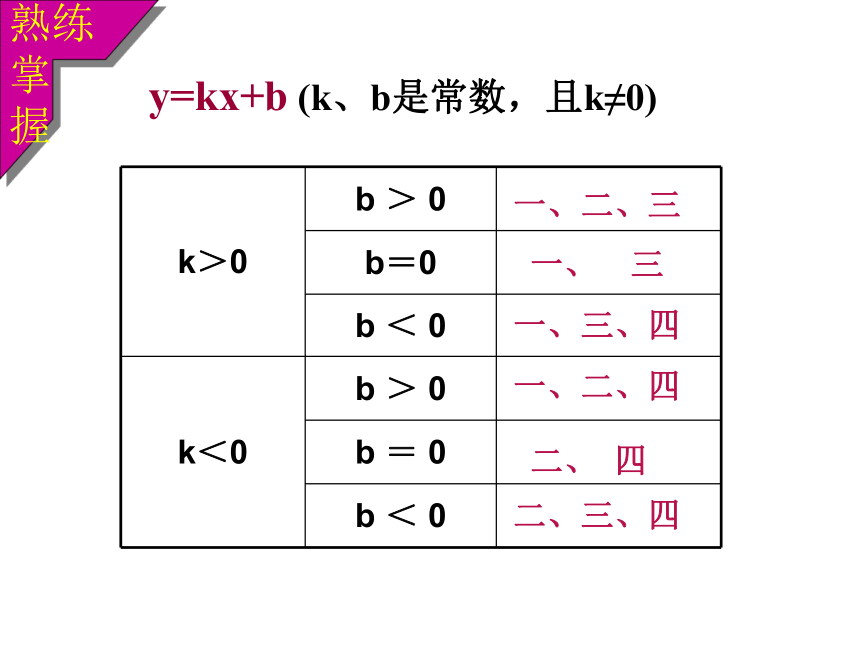
与x轴的交点为 (－b/k , 0 )y=kx+b (k、b是常数，且k≠0)一、二、三 一、 三一、三、四二、三、四 二、 四一、二、四熟练掌
握直线y=kx+b经过一、二、四象限，则
K 0, b 0．＜＞此时，直线y=bx-k的图象只能是( ) D请你判
断１.若一次函数y=x+b的图象过点A（1，-1），则b=__________。 -22 .根据如图所示的条件，求直线的表达式。 与y轴的交点为 (0 , b )
与x轴的交点为 (－b/k , 0 )先设出函数解析式，再根据条件确定解析式中未知的系数，从而具体写出这个式子的方法， －－待定系数法 求函数解析式的方法:要求理
解 3. 某一次函数的图象经过点A（5，１），且与直线y=2x-3无交点，
（1）求此一次函数表达式；
（2）求此一次函数与x轴、y轴的交点坐标；
（3）求此一次函数的图象与两坐标轴所围成的三角形的面积。
y=2x-94.一次函数y=k1x-4与正比例函数y=k2x的图象经过点（2，-1），
（1）分别求出这两个函数的表达式；
（2）求这两个函数的图象与x轴围成的三角形的面积。
5.
已知y-1与x成正比例，且x=2时，y=5.
(1)、写出y与x之间的函数关系式；
(2)、当x=-1时，求y的值；
(3)、当y=0时，求x的值。 6. 张大伯出去散步，从家走了20分钟，到了一个离家900米的阅报亭，看了10分钟报纸后，用了15分钟返回到家。下面哪个图象表示张大伯离家时间与距离之间的关系？ （ ）
时间（分）距离（米）0D请你判
断开启
智
慧 7.某医药研究所开发了一种新药，在试验药效时发现，如果成人按规定剂量服用，那么服药的一定时间内每毫升血液中含药量y（微克）随时间x（时）逐步增加,变化情况如图所示.6 2Ox/时y/微克（1）当x≤2时,y与x之间的函数关系式
是 。
y=3x（3）如果每毫升血液中含药量4微克或4微克以上时在治疗疾病是有效的，那么这个有效时间是多长?

（2）服药后2时，血液中含药量最高达每毫升6微克，接着每小时逐步衰减 微克。

求出当x≥2时y与x之间的函数关系式.
（1）说出甲、乙两物体的初始位置，并说明开始时谁前谁后？8.已知甲、乙两物体沿同一条直线同时、同向匀速运动，它们所经过的路程s与所需时间t之间的关系如图
所示.甲物体在离起点2米处，乙物体在起点。甲在前乙在后.请试一
试（3）求出两图象的交点坐标，并说明实际意义.2秒时乙物体追上甲物体。2秒前甲先乙后
2秒后乙先甲后。（2）分别求出甲、乙的路程s关于时间t的函数解析式.(2,3)（3）用恰当的方式表示费用y与路程s之间的关系。9.某市出租车计费方法如图所示，请根据图象回答下面的问题：（1）出租车的起步价是多少元？在多少路程内只收起步价？（2）起步价里程走完之后，每行驶1km需多少车费？（4）某外地客人坐出租车游览本市，车费为31元，试求出他乘车的里程。5元3km请练一
练 10.如图为甲、乙两名选手在一次自行车越野赛中，
路程y（千米）随时间x（分）变化的图象（
全程）．根据图象回答下列问题：
（１）比赛开始多少时间时，两人第一次相遇？
（２）这次比赛全程是多少千米？
（３）比赛开始多少时间时，两人第二次相遇？
挑战一下请你会
用１.梳理本章知识脉络，加强知识点的巩固和理解．
２.进一步学会函数的研究方法，提高解题的灵活性．
３.对综合性题目，会合理使用数学思想方法探究解决．用待定系数法解一次函数的解析式。一次函数y=kx+b的图象是一条直线,
k>0, y随x的增大而增大;
k<0 ,y随x的增大而减小.你今天的收获是什么呢？学会一次函数的应用. 学会一次函数的画图。k,b决定图象所经过的象限.k决定上升与下降b决定图象与y轴的交点位置.结束寄语严格性之于数学家,犹如道德之于人.
由“因”导“果”,执“果”索“因”.是探索证明思路的基本方法.