4.6图形的位似
图片预览




文档简介
课件16张PPT。课题:4.6 图形的位似
姓名:卢建章
学校:镇海应行久外语实验学校使用说明:
(1)运行环境:Microsoft Office PowerPoint 2003版本。
(2)内容介绍:本课件主要分:“知识回顾、情景引入、概念与定理、例题与练习、拓展与应用、课堂小结”六部分依次展开;操作时可依次点击进行教学; 制作者:卢建章
镇海应行久外语实验学校义务教育课程标准实验教科书浙江版数学4.6 图形的位似1. 前面我们已经学习了图形的哪些变换?平移:平移的方向,平移的距离.
旋转:旋转中心,旋转方向,旋转角度.
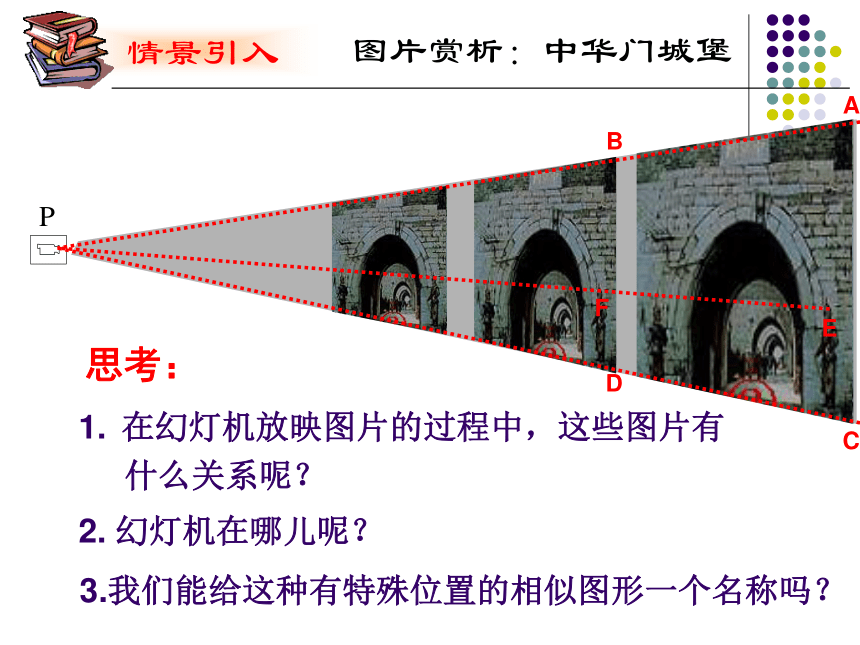
相似:相似比.对称(轴对称与轴对称图形,中心对称与中心对称图形):对称轴,对称中心.注:图形这些不同的变换是我们学习几何必不可少的重要工具,它不但装点了我们的生活,而且是学习后续知识的基础.下面请欣赏如下图形的变换ABCDEF图片赏析:中华门城堡在幻灯机放映图片的过程中,这些图片有
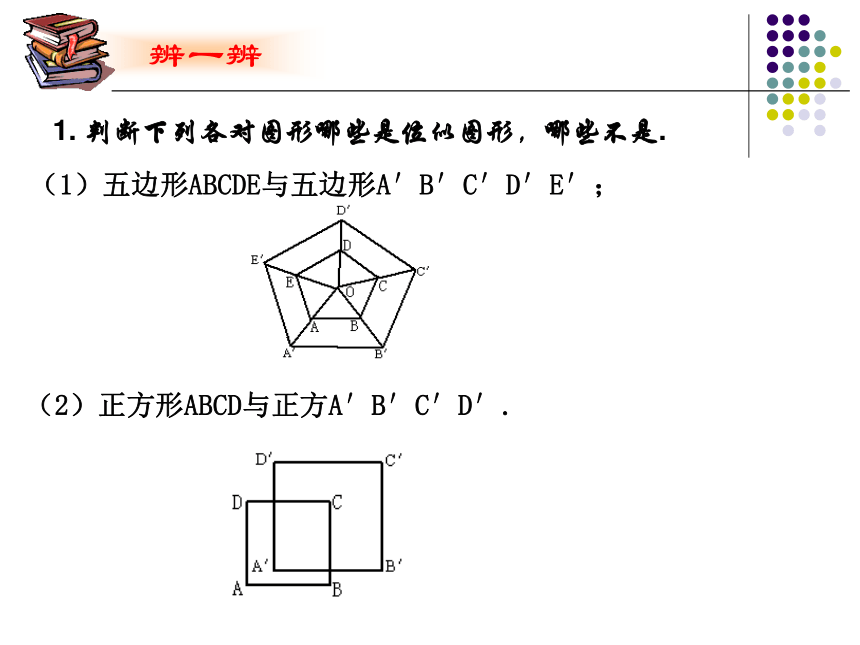
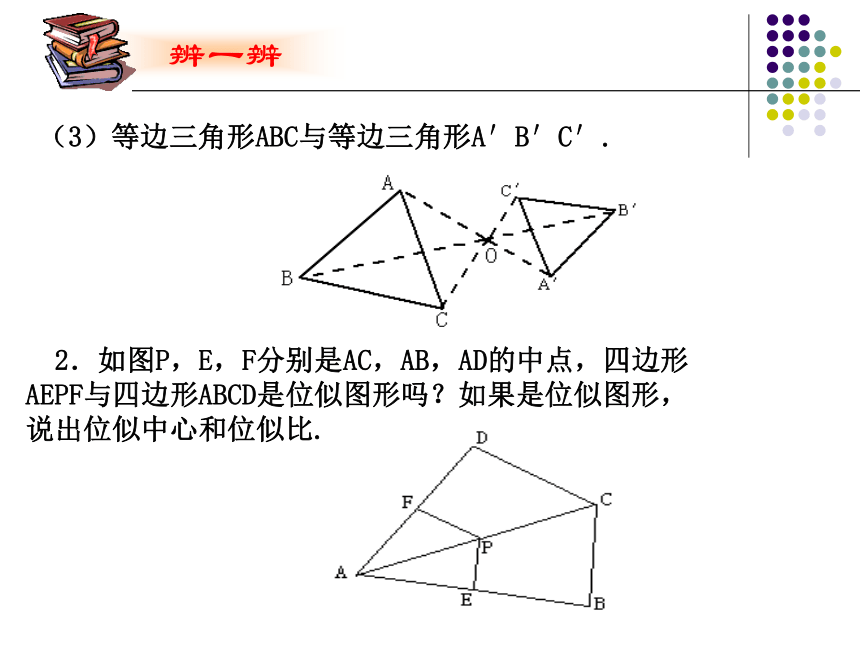
什么关系呢?2. 幻灯机在哪儿呢?思考:3.我们能给这种有特殊位置的相似图形一个名称吗?相似图形的特例1.位似图形的概念如果两个图形不仅形状相同,而且每组对应点所在的直线都经过同一点,那么这样的两个图形叫做位似图形,这个点叫做位似中心.如下面两个图形就是位似图形:显然,位似图形是相似图形的特殊情形,其相似比又叫做它们的位似比. 1. 判断下列各对图形哪些是位似图形,哪些不是. (1)五边形ABCDE与五边形A′B′C′D′E′; (2)正方形ABCD与正方A′B′C′D′. 2.如图P,E,F分别是AC,AB,AD的中点,四边形AEPF与四边形ABCD是位似图形吗?如果是位似图形,说出位似中心和位似比. (3)等边三角形ABC与等边三角形A′B′C′.2. 位似图形的性质 一般地,位似图形有以下性质:
位似图形上任意一对对应点到位似中心的距离之比等于位似比. 作位似图形 例:如图,请以坐标原点O为位似中心,作□ ABCD的位似图形,并把它的边长放大3倍. 分析:根据位似图形上任意一对对应点到位似中心的距离之比等于位似比,我们只要连结位似中心O和□ ABCD的各顶点,并把线段延长(或反向延长)到原来的3倍,就得到所求作图形的各个顶点.
作法如下:作法 1. 连结OA,OB,OC,OD.2. 分别延长OA,OB,OC,OD至G,C,E,F,使3. 依次连结GC,CE,EF,FG四边形GCEF就是所求作的四边形.
如果反向延长OA,OB,OC,OD,就得到四边形G’C’E’F’,也是所求作的四边形.作法如下:以坐标原点为位似中心的位似变换有以下性质:
若原图形上点的坐标为(x,y),像与原图形的位似比为k,则像上的对应点的坐标为(kx,ky)或(―kx,―ky). 想一想: 1.四边形GCEF与四边形G′C′E′F′具有怎样的对称性?
2.怎样运用像与原像对应点的坐标关系,画出以原点为位似中心的位似图形?开启智慧的钥匙课内练习: 1.如图,已知△ABC和点O.以O为位似中心,求作△ABC的位似图形,并把△ABC的边长缩小到原来的一半. 3. 已知图形F如图.选取适当的一点为位似中心,适当的比为位似比,作图形F的位似图形.使它和原图形组成一幅轴对称的图形.回味无穷位似图形的概念:
如果两个图形不仅形状相同,而且每组对应顶点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比.
位似图形的性质:
1.位似图形上的任意一对对应点到位似中心的距离之比等于位似比
2.以坐标原点为位似中心的位似变换有以下性质:若原图形上点的坐标为(x,y),像与原图形的位似比为k,则像上的对应点的坐标为(kx,ky)或(―kx,―ky)图形的变换:
对称,平移,旋转,相似,位似,…… 可以帮助我们真正了解数学的内在关系.下课了! 谢谢结束寄语
姓名:卢建章
学校:镇海应行久外语实验学校使用说明:
(1)运行环境:Microsoft Office PowerPoint 2003版本。
(2)内容介绍:本课件主要分:“知识回顾、情景引入、概念与定理、例题与练习、拓展与应用、课堂小结”六部分依次展开;操作时可依次点击进行教学; 制作者:卢建章
镇海应行久外语实验学校义务教育课程标准实验教科书浙江版数学4.6 图形的位似1. 前面我们已经学习了图形的哪些变换?平移:平移的方向,平移的距离.
旋转:旋转中心,旋转方向,旋转角度.
相似:相似比.对称(轴对称与轴对称图形,中心对称与中心对称图形):对称轴,对称中心.注:图形这些不同的变换是我们学习几何必不可少的重要工具,它不但装点了我们的生活,而且是学习后续知识的基础.下面请欣赏如下图形的变换ABCDEF图片赏析:中华门城堡在幻灯机放映图片的过程中,这些图片有
什么关系呢?2. 幻灯机在哪儿呢?思考:3.我们能给这种有特殊位置的相似图形一个名称吗?相似图形的特例1.位似图形的概念如果两个图形不仅形状相同,而且每组对应点所在的直线都经过同一点,那么这样的两个图形叫做位似图形,这个点叫做位似中心.如下面两个图形就是位似图形:显然,位似图形是相似图形的特殊情形,其相似比又叫做它们的位似比. 1. 判断下列各对图形哪些是位似图形,哪些不是. (1)五边形ABCDE与五边形A′B′C′D′E′; (2)正方形ABCD与正方A′B′C′D′. 2.如图P,E,F分别是AC,AB,AD的中点,四边形AEPF与四边形ABCD是位似图形吗?如果是位似图形,说出位似中心和位似比. (3)等边三角形ABC与等边三角形A′B′C′.2. 位似图形的性质 一般地,位似图形有以下性质:
位似图形上任意一对对应点到位似中心的距离之比等于位似比. 作位似图形 例:如图,请以坐标原点O为位似中心,作□ ABCD的位似图形,并把它的边长放大3倍. 分析:根据位似图形上任意一对对应点到位似中心的距离之比等于位似比,我们只要连结位似中心O和□ ABCD的各顶点,并把线段延长(或反向延长)到原来的3倍,就得到所求作图形的各个顶点.
作法如下:作法 1. 连结OA,OB,OC,OD.2. 分别延长OA,OB,OC,OD至G,C,E,F,使3. 依次连结GC,CE,EF,FG四边形GCEF就是所求作的四边形.
如果反向延长OA,OB,OC,OD,就得到四边形G’C’E’F’,也是所求作的四边形.作法如下:以坐标原点为位似中心的位似变换有以下性质:
若原图形上点的坐标为(x,y),像与原图形的位似比为k,则像上的对应点的坐标为(kx,ky)或(―kx,―ky). 想一想: 1.四边形GCEF与四边形G′C′E′F′具有怎样的对称性?
2.怎样运用像与原像对应点的坐标关系,画出以原点为位似中心的位似图形?开启智慧的钥匙课内练习: 1.如图,已知△ABC和点O.以O为位似中心,求作△ABC的位似图形,并把△ABC的边长缩小到原来的一半. 3. 已知图形F如图.选取适当的一点为位似中心,适当的比为位似比,作图形F的位似图形.使它和原图形组成一幅轴对称的图形.回味无穷位似图形的概念:
如果两个图形不仅形状相同,而且每组对应顶点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比.
位似图形的性质:
1.位似图形上的任意一对对应点到位似中心的距离之比等于位似比
2.以坐标原点为位似中心的位似变换有以下性质:若原图形上点的坐标为(x,y),像与原图形的位似比为k,则像上的对应点的坐标为(kx,ky)或(―kx,―ky)图形的变换:
对称,平移,旋转,相似,位似,…… 可以帮助我们真正了解数学的内在关系.下课了! 谢谢结束寄语
同课章节目录
