浙教版数学八年级上册 第1章——补充证明过程训练(3) (无答案)
文档属性
| 名称 | 浙教版数学八年级上册 第1章——补充证明过程训练(3) (无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 194.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 14:58:19 | ||
图片预览




文档简介
浙教版数学八年级上册第1章
补充证明过程训练3
1.把下面的说理过程补充完整:
已知:如图,,,.线段AB和线段DE平行吗?请说明理由.
解:理由:
(已知).
(________)
即
又(________)
(________)
(________).
(________).
2.阅读、填空并将说理过程补充完整:如图,已知点D、E分别在△ABC的边AB、AC上,且∠AED=∠B,延长DE与BC的延长线交于点F,∠BAC和∠BFD的角平分线交于点G.那么AG与FG的位置关系如何?为什么?
解:AG⊥FG.将AG、DF的交点记为点P,延长AG交BC于点Q.
因为AG、FG分别平分∠BAC和∠BFD(已知)
所以∠BAG= , (角平分线定义)
又因为∠FPQ= +∠AED, = +∠B
(三角形的一个外角等于与它不相邻的两个内角的和)
∠AED=∠B(已知)
所以∠FPQ= (等式性质)
(请完成以下说理过程)
3.填空:把下面的推理过程补充完整,并在括号内注明理由,
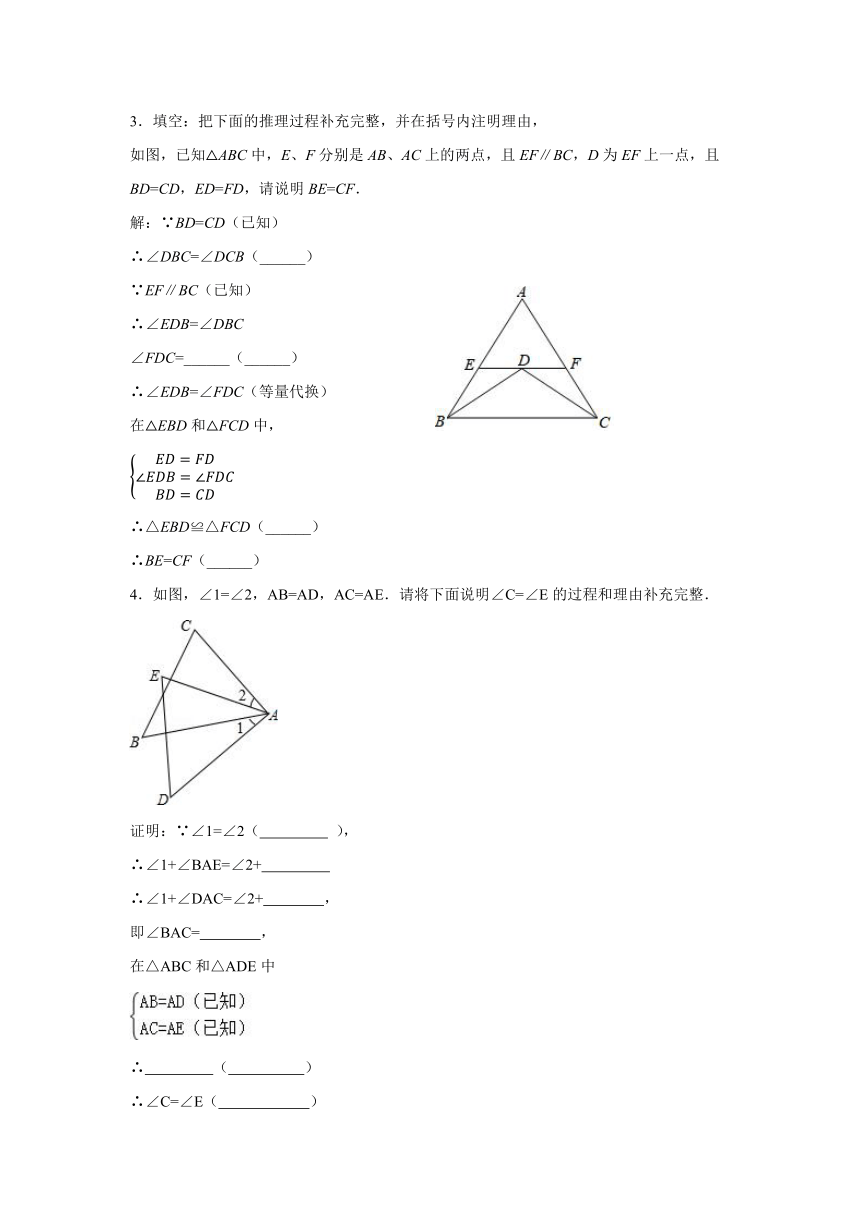
如图,已知△ABC中,E、F分别是AB、AC上的两点,且EF∥BC,D为EF上一点,且BD=CD,ED=FD,请说明BE=CF.
解:∵BD=CD(已知)
∴∠DBC=∠DCB(______)
∵EF∥BC(已知)
∴∠EDB=∠DBC
∠FDC=______(______)
∴∠EDB=∠FDC(等量代换)
在△EBD和△FCD中,
∴△EBD≌△FCD(______)
∴BE=CF(______)
4.如图,∠1=∠2,AB=AD,AC=AE.请将下面说明∠C=∠E的过程和理由补充完整.
证明:∵∠1=∠2( ),
∴∠1+∠BAE=∠2+
∴∠1+∠DAC=∠2+ ,
即∠BAC= ,
在△ABC和△ADE中
∴ ( )
∴∠C=∠E( )
5.把下面推理过程补充完整,在括号内注明理由:
已知:如图,BC//EF,AB=DE,BC=EF,试说明∠C=∠F;
解:∵BC//EF(已知)
∴∠ABC=∠__________ _________________________
在△ABC与△DEF中,
∵
∴△ABC≌△DEF _______
∴∠C=∠F ____________________________
6.把下面的推理过程补充完整,并在括号内注明理由.
如图,点B、D在线段AE上,BC∥EF,AD=BE,BC=EF,
试说明:(1)∠C=∠F;(2)AC∥DF.
解:(1)∵AD=BE(已知)
∴AD+DB=DB+BE( )
即AB=DE
∵BC∥EF(已知)
∴∠ABC=∠ ( )
又∵BC=EF(已知)
∴△ABC≌△DEF( )
∴∠C=∠F,∠A=∠FDE( )
∴AC∥DF( )
7.已知:如图,点B、E、C、F在同一条直线上,且AB=DE,AC=DF,BE=CF.求证:AB∥DE.请将下面的过程和理由补充完整
证明:∵BE=CF ( )
∴BE+EC=CF+EC即 .
在△ABC和△DEF中,
AB=DE( 已知)
AC=DF( )
BC= ( )
∴△ABC≌△DEF( )
∴∠ABC=∠DEF ( )
∴AB∥DE ( )
8.填空:(将下面的推理过程及依据补充完整)
已知:△ABC的高AD所在直线与高BE所在直线相交于点F,过点F作FGBC,交直线AB于点G.如图,且∠ABC=45°.
求证:①△BDF≌△ADC;②FG+DC=AD;
①证明:∵AD,BE为高
∴∠ADB=∠BEC=90°
∵∠ABC=45°
∴∠BAD=∠ =45°
∴AD= ;
∵∠BEC=90°
∴∠CBE+∠C=90°( )
又∵∠DAC+∠C=90°
∴∠CBE=∠DAC( )
在△FDB和△CDA中,
∵∠FDB=∠CDA=90°,
AD=BD
∠CBE=∠DAC
∴△FDB≌△CDA( )
②∵△FDB≌△CDA,
∴DF=DC( )
∵GFBC
∴∠AGF=∠ABC=45°,( )
∴∠AGF=∠ ,
∴FA=FG;
∴FG+DC=FA+DF=AD.
9.如图,在中,,、分别是、边上的点,且平分,
(1)试说明,请将下面的推理过程补充完整.
解:∵
∴
∵
∴
∵平分
∴______(__________________________)
在和中,
∵
∴(_____________)
∴(___________________)
(2)若,,且的面积为6.
①______;
②点在直线上运动,如果的面积为,则的长为______.
10.请将以下推导过程补充完整.
如图,点在线段上,,,,平分.
求证:.
证明:∵
∴
在和中
∴(________)
∴(___________)
∵平分
∴________
在和中
∴
11.如图,点E、F在BD上,且,,,试说明:点O是AC的中点.请你在横线上补充其推理过程或理由.
解:因为
所以,即
因为,
所以 (理由:SSS)
所以(理由: )
因为(理由: )
所以(理由: )
所以 (理由:全等三角形对应边相等)
所以点O是AC的中点.
12.请将下面的说理过程和理由补充完整.
已知:如图,AB∥DE,,.说明AC∥DF的理由.
解:∵AB∥DE,
∴______.( )
在和中,.
∴( )
∴______.( )
∵,
∴______.( )
∴AC∥DF.( )
13.如图,点在线段上,//,,.
(1)求作的平分线(要求:尺规作图,保留作图痕迹,不写作法);
(2)若的平分线交于点,试证明:.请将以下推导过程补充完整.
证明:∵AB//CE
在和中
( )
平分
__________
在和中
.
14.如图,在长方形中,,垂直平分分别交,于,,求证:.(请你将下面的推理过程中的横线空白处补充完整.)
解:∵(____________)
∴(____________)
∵垂直平分(已知)
∴(线段垂直平分线的定义)
在和中,
,
∴(____________)
∴(____________)
又∵垂直平分(已知)
∴__________(线段垂直平分线上的点到线段两端的距离相等)
∴(__________).
15.如图,,点D,E分别在AC,AB上,且.
求证:.
请将下列证明过程补充完整:
证明:在和中,
∵
∴( )
∴(____________)
16.如图,与中,与交于点,且.求证∶.请将下列证明过程补充完整∶
证明∶在和中,
(________)
_______=_______(对顶角相等)
=(________)(已知)
(________)
(_______________)
补充证明过程训练3
1.把下面的说理过程补充完整:
已知:如图,,,.线段AB和线段DE平行吗?请说明理由.
解:理由:
(已知).
(________)
即
又(________)
(________)
(________).
(________).
2.阅读、填空并将说理过程补充完整:如图,已知点D、E分别在△ABC的边AB、AC上,且∠AED=∠B,延长DE与BC的延长线交于点F,∠BAC和∠BFD的角平分线交于点G.那么AG与FG的位置关系如何?为什么?
解:AG⊥FG.将AG、DF的交点记为点P,延长AG交BC于点Q.
因为AG、FG分别平分∠BAC和∠BFD(已知)
所以∠BAG= , (角平分线定义)
又因为∠FPQ= +∠AED, = +∠B
(三角形的一个外角等于与它不相邻的两个内角的和)
∠AED=∠B(已知)
所以∠FPQ= (等式性质)
(请完成以下说理过程)
3.填空:把下面的推理过程补充完整,并在括号内注明理由,
如图,已知△ABC中,E、F分别是AB、AC上的两点,且EF∥BC,D为EF上一点,且BD=CD,ED=FD,请说明BE=CF.
解:∵BD=CD(已知)
∴∠DBC=∠DCB(______)
∵EF∥BC(已知)
∴∠EDB=∠DBC
∠FDC=______(______)
∴∠EDB=∠FDC(等量代换)
在△EBD和△FCD中,
∴△EBD≌△FCD(______)
∴BE=CF(______)
4.如图,∠1=∠2,AB=AD,AC=AE.请将下面说明∠C=∠E的过程和理由补充完整.
证明:∵∠1=∠2( ),
∴∠1+∠BAE=∠2+
∴∠1+∠DAC=∠2+ ,
即∠BAC= ,
在△ABC和△ADE中
∴ ( )
∴∠C=∠E( )
5.把下面推理过程补充完整,在括号内注明理由:
已知:如图,BC//EF,AB=DE,BC=EF,试说明∠C=∠F;
解:∵BC//EF(已知)
∴∠ABC=∠__________ _________________________
在△ABC与△DEF中,
∵
∴△ABC≌△DEF _______
∴∠C=∠F ____________________________
6.把下面的推理过程补充完整,并在括号内注明理由.
如图,点B、D在线段AE上,BC∥EF,AD=BE,BC=EF,
试说明:(1)∠C=∠F;(2)AC∥DF.
解:(1)∵AD=BE(已知)
∴AD+DB=DB+BE( )
即AB=DE
∵BC∥EF(已知)
∴∠ABC=∠ ( )
又∵BC=EF(已知)
∴△ABC≌△DEF( )
∴∠C=∠F,∠A=∠FDE( )
∴AC∥DF( )
7.已知:如图,点B、E、C、F在同一条直线上,且AB=DE,AC=DF,BE=CF.求证:AB∥DE.请将下面的过程和理由补充完整
证明:∵BE=CF ( )
∴BE+EC=CF+EC即 .
在△ABC和△DEF中,
AB=DE( 已知)
AC=DF( )
BC= ( )
∴△ABC≌△DEF( )
∴∠ABC=∠DEF ( )
∴AB∥DE ( )
8.填空:(将下面的推理过程及依据补充完整)
已知:△ABC的高AD所在直线与高BE所在直线相交于点F,过点F作FGBC,交直线AB于点G.如图,且∠ABC=45°.
求证:①△BDF≌△ADC;②FG+DC=AD;
①证明:∵AD,BE为高
∴∠ADB=∠BEC=90°
∵∠ABC=45°
∴∠BAD=∠ =45°
∴AD= ;
∵∠BEC=90°
∴∠CBE+∠C=90°( )
又∵∠DAC+∠C=90°
∴∠CBE=∠DAC( )
在△FDB和△CDA中,
∵∠FDB=∠CDA=90°,
AD=BD
∠CBE=∠DAC
∴△FDB≌△CDA( )
②∵△FDB≌△CDA,
∴DF=DC( )
∵GFBC
∴∠AGF=∠ABC=45°,( )
∴∠AGF=∠ ,
∴FA=FG;
∴FG+DC=FA+DF=AD.
9.如图,在中,,、分别是、边上的点,且平分,
(1)试说明,请将下面的推理过程补充完整.
解:∵
∴
∵
∴
∵平分
∴______(__________________________)
在和中,
∵
∴(_____________)
∴(___________________)
(2)若,,且的面积为6.
①______;
②点在直线上运动,如果的面积为,则的长为______.
10.请将以下推导过程补充完整.
如图,点在线段上,,,,平分.
求证:.
证明:∵
∴
在和中
∴(________)
∴(___________)
∵平分
∴________
在和中
∴
11.如图,点E、F在BD上,且,,,试说明:点O是AC的中点.请你在横线上补充其推理过程或理由.
解:因为
所以,即
因为,
所以 (理由:SSS)
所以(理由: )
因为(理由: )
所以(理由: )
所以 (理由:全等三角形对应边相等)
所以点O是AC的中点.
12.请将下面的说理过程和理由补充完整.
已知:如图,AB∥DE,,.说明AC∥DF的理由.
解:∵AB∥DE,
∴______.( )
在和中,.
∴( )
∴______.( )
∵,
∴______.( )
∴AC∥DF.( )
13.如图,点在线段上,//,,.
(1)求作的平分线(要求:尺规作图,保留作图痕迹,不写作法);
(2)若的平分线交于点,试证明:.请将以下推导过程补充完整.
证明:∵AB//CE
在和中
( )
平分
__________
在和中
.
14.如图,在长方形中,,垂直平分分别交,于,,求证:.(请你将下面的推理过程中的横线空白处补充完整.)
解:∵(____________)
∴(____________)
∵垂直平分(已知)
∴(线段垂直平分线的定义)
在和中,
,
∴(____________)
∴(____________)
又∵垂直平分(已知)
∴__________(线段垂直平分线上的点到线段两端的距离相等)
∴(__________).
15.如图,,点D,E分别在AC,AB上,且.
求证:.
请将下列证明过程补充完整:
证明:在和中,
∵
∴( )
∴(____________)
16.如图,与中,与交于点,且.求证∶.请将下列证明过程补充完整∶
证明∶在和中,
(________)
_______=_______(对顶角相等)
=(________)(已知)
(________)
(_______________)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
