浙教版七年级数学每日一题56-60角的旋转探究问题(含答案)
文档属性
| 名称 | 浙教版七年级数学每日一题56-60角的旋转探究问题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 23:36:59 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
七年级每日一题56——角的旋转探究问题
班级 姓名 学号
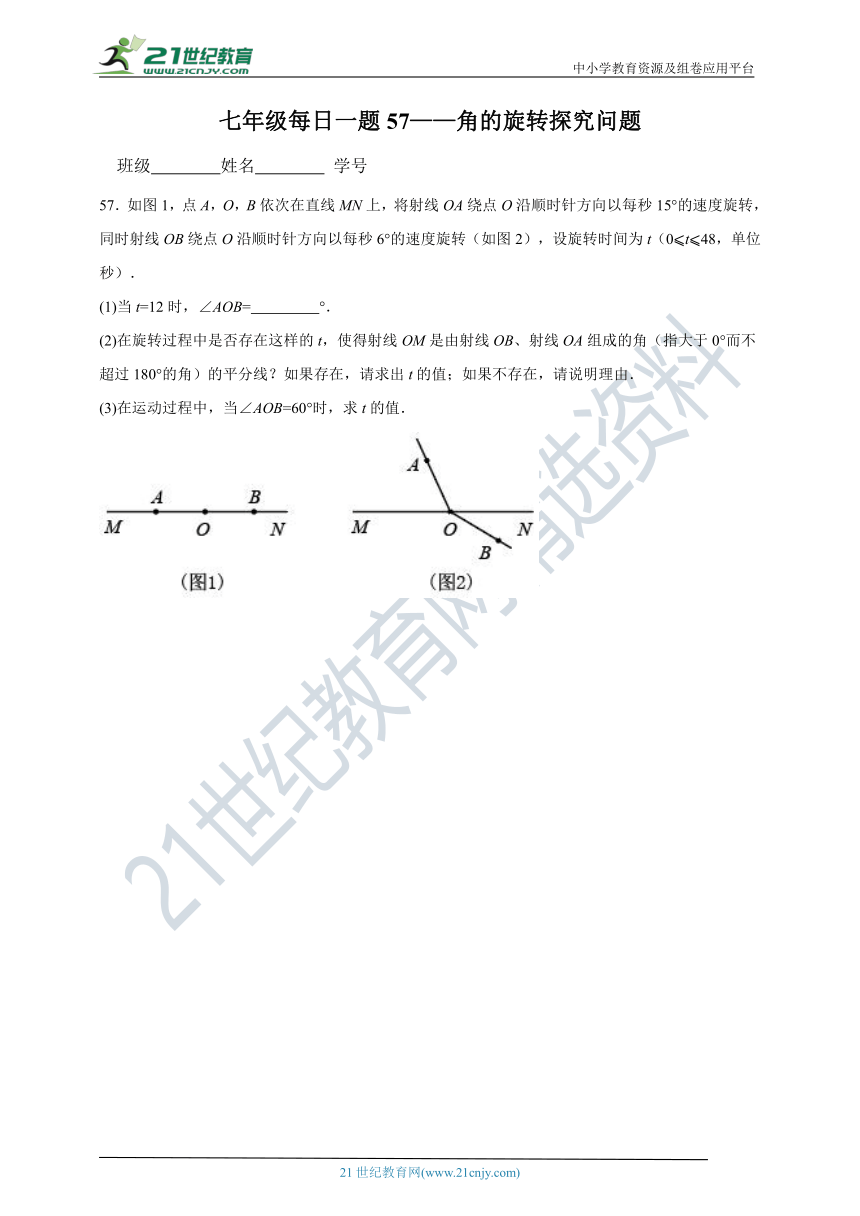
56.如图1,点O为直线上一点,过点O作射线,使,将一直角三角板的直角顶点放在点O处,一边在射线上,另一边在直线的下方.
(1)将图1中的三角板绕点O逆时针旋转至图2,使点N在的反向延长线上,请直接写出图中的度数;
(2)将图1中的三角板绕点O顺时针旋转至图3,使一边在的内部,且恰好平分,求的度数;
(3)将图1中的三角尺绕点O顺时针旋转至图4,使在内部,请探究与之间的数量关系,并说明理由.
七年级每日一题57——角的旋转探究问题
班级 姓名 学号
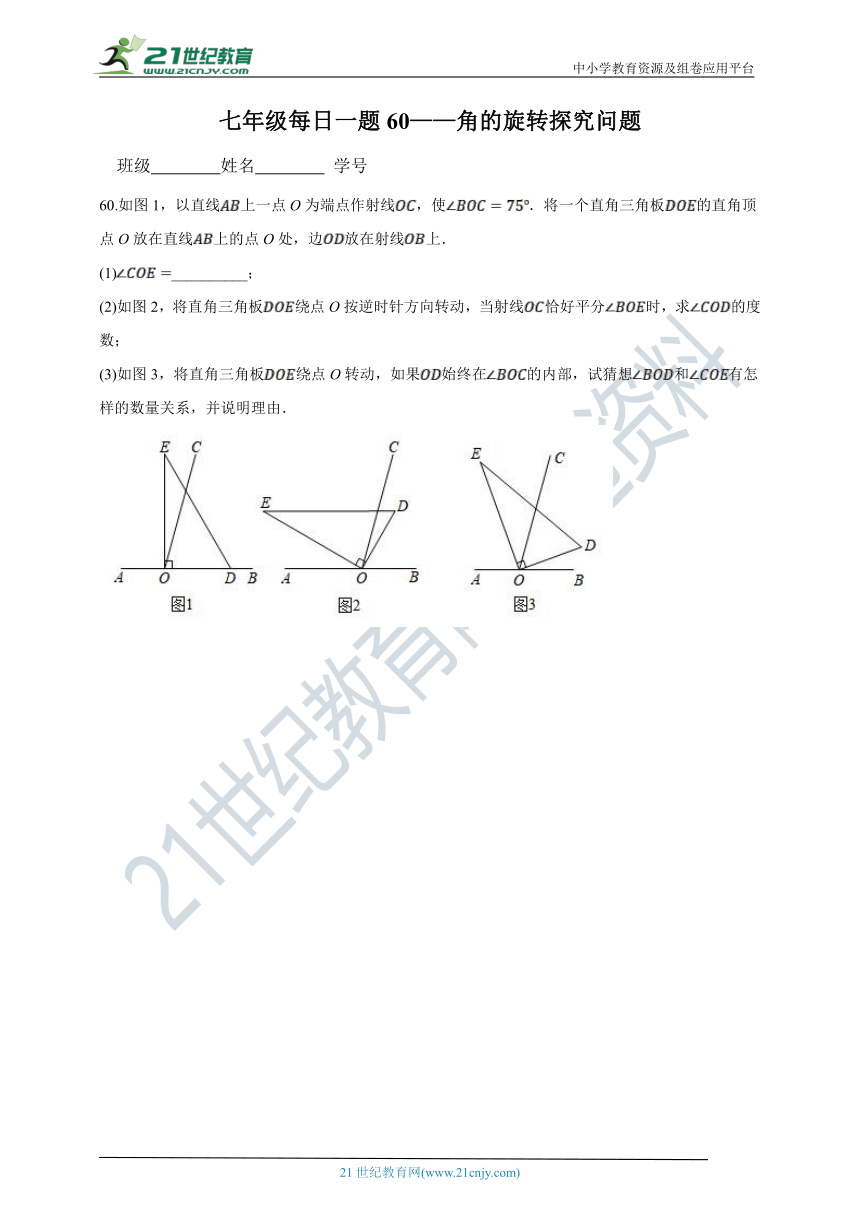
57.如图1,点A,O,B依次在直线MN上,将射线OA绕点O沿顺时针方向以每秒15°的速度旋转,同时射线OB绕点O沿顺时针方向以每秒6°的速度旋转(如图2),设旋转时间为t(0 t 48,单位秒).
(1)当t=12时,∠AOB= °.
(2)在旋转过程中是否存在这样的t,使得射线OM是由射线OB、射线OA组成的角(指大于0°而不超过180°的角)的平分线?如果存在,请求出t的值;如果不存在,请说明理由.
(3)在运动过程中,当∠AOB=60°时,求t的值.
七年级每日一题58——角的旋转探究问题
班级 姓名 学号
58.如图,直线CD,EF相交于点O,射线OA在∠COF的内部,∠DOF=∠AOD.
(1)如图1,若∠AOC=120°,求∠EOC的度数;
(2)如图2,若∠AOC=α(60°<α<180°),将射线OA绕点O逆时针旋转60°,到OB,
①求∠EOB的度数(用含α的式子表示);
②观察①中的结果,直接写出∠AOC,∠EOB之间的数量关系.
(3) 如图3 ,0°<∠AOC <120°,将射线OA绕点O顺时针旋转60°,到OB,请直接写出∠AOC,∠EOB之间的数量关系.
七年级每日一题59——角的旋转探究问题
班级 姓名 学号
59.已知O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图①,若∠AOC=30°,求∠COE,∠DOB的度数.
(2)如图①,若∠AOC=α,求∠DOE的度数(用含α的代数式表示).
(3)将图①中的∠COD绕顶点O顺时针旋转至图②的位置,探究∠AOC与∠DOE的度数之间的数量关系,并说明理由.
七年级每日一题60——角的旋转探究问题
班级 姓名 学号
60.如图1,以直线上一点O为端点作射线,使.将一个直角三角板的直角顶点O放在直线上的点O处,边放在射线上.
(1)__________;
(2)如图2,将直角三角板绕点O按逆时针方向转动,当射线恰好平分时,求的度数;
(3)如图3,将直角三角板绕点O转动,如果始终在的内部,试猜想和有怎样的数量关系,并说明理由.
七年级每日一题56 答案
56.(1)解:∵,
∴,
∴,
∵,
∴;
(2)解:∵,平分,
∴,
∵,
∴;
(3)解:,
理由是:∵,,
∴,,
∴,
∴,
故与之间的数量关系为:.
七年级每日一题57 答案
57.【详解】(1)解:当t=12时,∠AOM=15°×12=180°,∠BON=5°×12=60°,
∴∠AOB=180° ∠AOM+∠BON=60°,
故答案为:60°.
(2)存在满足条件的t值。
①∵OA旋转一周所需时间为:360°÷15°=24(秒),
此时,∠BON=5°×24=120°,即OA已经旋转过OB的位置,
若OM平分∠AOB且0°<∠AOB<180°,位置如图1,
∴∠AOM=(15t 360)°,∠BOM=(180 5t)°,
∴15t 360=180 5t,解得:t=27,
②若OM平分∠BOA且0°<∠BOA<180°,位置如下图2,
∴∠AOM=(720-15t)°,∠BOM=(5t-180)°,
∴720-15t=5t-180,解得:t=45,
(3)(3)①如图3,当∠AOB第一次达到60°时,OA比OB多转了(180 60)°,得:
15t 5t=180° 60°,解得:t=12,
②如图3,当∠AOB第二次达到60°时,OA比OB多转了(180+60)°,得:
15t 5t=180°+60°,解得:t=24,
③如图5,当∠AOB第三次达到60°时,OA比OB多转了(180+360 60)°,
得:15t 5t=180°+360° 60°,
解得:t=48,符合题意,
综上所述,当∠AOB=60°时,t=12或24或48.
七年级每日一题58 答案
58.(1)解:∵∠AOC=120°,
∴∠AOD=180°-∠AOC=180°-120°=60°,
∴∠DOF=∠AOD=20°, ∴∠EOC=∠DOF=20°;
(2)解:①∵∠AOC=α, ∴∠AOD=180°-α,
∴∠DOF=∠AOD=60°-, ∴∠EOC=∠DOF=60°-,
由题意得:∠AOB=60°, ∴∠BOC=α-60°,
∴∠EOB=∠EOC+∠BOC=60°-+α-60°=;
②观察①中结果可得:∠EOB=,
证明:∵∠AOD=180°-∠AOC,∠BOC=∠AOC-∠AOB=∠AOC-60°,
∴∠DOF=∠AOD=60°-∠AOC,
∴∠EOC=∠DOF=60°-∠AOC,
∴∠EOB=∠EOC+∠BOC=60°-∠AOC+∠AOC-60°=∠AOC;
(3)解:①当0°<∠AOC ≤90°时,
如图,∵∠AOD=180°-∠AOC,∠BOC=∠AOC+∠AOB=∠AOC+60°,
∴∠DOF=∠AOD=60°-∠AOC,
∴∠EOC=∠DOF=60°-∠AOC,
∴∠EOB=∠EOC+∠BOC=60°-∠AOC+∠AOC+60°=∠AOC+120°.
②当90°<∠AOC ≤120°时,
如图,∵∠AOD=180°-∠AOC,∠BOC=∠AOC+∠AOB=∠AOC+60°,
∴∠DOF=∠AOD=60°-∠AOC,
∴∠EOC=∠DOF=60°-∠AOC,
∴∠EOC+∠BOC=60°-∠AOC+∠AOC+60°=∠AOC+120°,
∴∠EOB=360°-(∠EOC+∠BOC)=360°-∠AOC-120°=240°-∠AOC.
七年级每日一题59 答案
59.(1)解:,是直角,
,,
,
平分,
;
(2),是直角,
,,
,
平分,
;
.
(3).理由如下:
设,
是直角,
,,
平分,
;
.
即.
七年级每日一题60 答案
【详解】(1)解:(1)如图①,∠COE=∠DOE-∠BOC=90°-75°=15°.
故答案为:15°.
(2)解:∵OC平分∠BOE,∠BOC=75°
∴∠EOB=2∠EOC=150°,
∴∠EOC=75°
∵∠DOE=90°
∴∠COD=∠DOE-∠EOC=90°-75°=15°.
(3)解:∠COE-∠BOD=15°,理由如下:
如图③,∵∠BOD+∠COD=∠BOC=75°,∠COE+∠COD=∠DOE=90°,
∴(∠COE+∠COD)-(∠BOD+∠COD)
=∠COE+∠COD-∠BOD-∠COD
=∠DOE-∠BOC
=90°-75°
=15°,
即∠COE-∠BOD=15°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
七年级每日一题56——角的旋转探究问题
班级 姓名 学号
56.如图1,点O为直线上一点,过点O作射线,使,将一直角三角板的直角顶点放在点O处,一边在射线上,另一边在直线的下方.
(1)将图1中的三角板绕点O逆时针旋转至图2,使点N在的反向延长线上,请直接写出图中的度数;
(2)将图1中的三角板绕点O顺时针旋转至图3,使一边在的内部,且恰好平分,求的度数;
(3)将图1中的三角尺绕点O顺时针旋转至图4,使在内部,请探究与之间的数量关系,并说明理由.
七年级每日一题57——角的旋转探究问题
班级 姓名 学号
57.如图1,点A,O,B依次在直线MN上,将射线OA绕点O沿顺时针方向以每秒15°的速度旋转,同时射线OB绕点O沿顺时针方向以每秒6°的速度旋转(如图2),设旋转时间为t(0 t 48,单位秒).
(1)当t=12时,∠AOB= °.
(2)在旋转过程中是否存在这样的t,使得射线OM是由射线OB、射线OA组成的角(指大于0°而不超过180°的角)的平分线?如果存在,请求出t的值;如果不存在,请说明理由.
(3)在运动过程中,当∠AOB=60°时,求t的值.
七年级每日一题58——角的旋转探究问题
班级 姓名 学号
58.如图,直线CD,EF相交于点O,射线OA在∠COF的内部,∠DOF=∠AOD.
(1)如图1,若∠AOC=120°,求∠EOC的度数;
(2)如图2,若∠AOC=α(60°<α<180°),将射线OA绕点O逆时针旋转60°,到OB,
①求∠EOB的度数(用含α的式子表示);
②观察①中的结果,直接写出∠AOC,∠EOB之间的数量关系.
(3) 如图3 ,0°<∠AOC <120°,将射线OA绕点O顺时针旋转60°,到OB,请直接写出∠AOC,∠EOB之间的数量关系.
七年级每日一题59——角的旋转探究问题
班级 姓名 学号
59.已知O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图①,若∠AOC=30°,求∠COE,∠DOB的度数.
(2)如图①,若∠AOC=α,求∠DOE的度数(用含α的代数式表示).
(3)将图①中的∠COD绕顶点O顺时针旋转至图②的位置,探究∠AOC与∠DOE的度数之间的数量关系,并说明理由.
七年级每日一题60——角的旋转探究问题
班级 姓名 学号
60.如图1,以直线上一点O为端点作射线,使.将一个直角三角板的直角顶点O放在直线上的点O处,边放在射线上.
(1)__________;
(2)如图2,将直角三角板绕点O按逆时针方向转动,当射线恰好平分时,求的度数;
(3)如图3,将直角三角板绕点O转动,如果始终在的内部,试猜想和有怎样的数量关系,并说明理由.
七年级每日一题56 答案
56.(1)解:∵,
∴,
∴,
∵,
∴;
(2)解:∵,平分,
∴,
∵,
∴;
(3)解:,
理由是:∵,,
∴,,
∴,
∴,
故与之间的数量关系为:.
七年级每日一题57 答案
57.【详解】(1)解:当t=12时,∠AOM=15°×12=180°,∠BON=5°×12=60°,
∴∠AOB=180° ∠AOM+∠BON=60°,
故答案为:60°.
(2)存在满足条件的t值。
①∵OA旋转一周所需时间为:360°÷15°=24(秒),
此时,∠BON=5°×24=120°,即OA已经旋转过OB的位置,
若OM平分∠AOB且0°<∠AOB<180°,位置如图1,
∴∠AOM=(15t 360)°,∠BOM=(180 5t)°,
∴15t 360=180 5t,解得:t=27,
②若OM平分∠BOA且0°<∠BOA<180°,位置如下图2,
∴∠AOM=(720-15t)°,∠BOM=(5t-180)°,
∴720-15t=5t-180,解得:t=45,
(3)(3)①如图3,当∠AOB第一次达到60°时,OA比OB多转了(180 60)°,得:
15t 5t=180° 60°,解得:t=12,
②如图3,当∠AOB第二次达到60°时,OA比OB多转了(180+60)°,得:
15t 5t=180°+60°,解得:t=24,
③如图5,当∠AOB第三次达到60°时,OA比OB多转了(180+360 60)°,
得:15t 5t=180°+360° 60°,
解得:t=48,符合题意,
综上所述,当∠AOB=60°时,t=12或24或48.
七年级每日一题58 答案
58.(1)解:∵∠AOC=120°,
∴∠AOD=180°-∠AOC=180°-120°=60°,
∴∠DOF=∠AOD=20°, ∴∠EOC=∠DOF=20°;
(2)解:①∵∠AOC=α, ∴∠AOD=180°-α,
∴∠DOF=∠AOD=60°-, ∴∠EOC=∠DOF=60°-,
由题意得:∠AOB=60°, ∴∠BOC=α-60°,
∴∠EOB=∠EOC+∠BOC=60°-+α-60°=;
②观察①中结果可得:∠EOB=,
证明:∵∠AOD=180°-∠AOC,∠BOC=∠AOC-∠AOB=∠AOC-60°,
∴∠DOF=∠AOD=60°-∠AOC,
∴∠EOC=∠DOF=60°-∠AOC,
∴∠EOB=∠EOC+∠BOC=60°-∠AOC+∠AOC-60°=∠AOC;
(3)解:①当0°<∠AOC ≤90°时,
如图,∵∠AOD=180°-∠AOC,∠BOC=∠AOC+∠AOB=∠AOC+60°,
∴∠DOF=∠AOD=60°-∠AOC,
∴∠EOC=∠DOF=60°-∠AOC,
∴∠EOB=∠EOC+∠BOC=60°-∠AOC+∠AOC+60°=∠AOC+120°.
②当90°<∠AOC ≤120°时,
如图,∵∠AOD=180°-∠AOC,∠BOC=∠AOC+∠AOB=∠AOC+60°,
∴∠DOF=∠AOD=60°-∠AOC,
∴∠EOC=∠DOF=60°-∠AOC,
∴∠EOC+∠BOC=60°-∠AOC+∠AOC+60°=∠AOC+120°,
∴∠EOB=360°-(∠EOC+∠BOC)=360°-∠AOC-120°=240°-∠AOC.
七年级每日一题59 答案
59.(1)解:,是直角,
,,
,
平分,
;
(2),是直角,
,,
,
平分,
;
.
(3).理由如下:
设,
是直角,
,,
平分,
;
.
即.
七年级每日一题60 答案
【详解】(1)解:(1)如图①,∠COE=∠DOE-∠BOC=90°-75°=15°.
故答案为:15°.
(2)解:∵OC平分∠BOE,∠BOC=75°
∴∠EOB=2∠EOC=150°,
∴∠EOC=75°
∵∠DOE=90°
∴∠COD=∠DOE-∠EOC=90°-75°=15°.
(3)解:∠COE-∠BOD=15°,理由如下:
如图③,∵∠BOD+∠COD=∠BOC=75°,∠COE+∠COD=∠DOE=90°,
∴(∠COE+∠COD)-(∠BOD+∠COD)
=∠COE+∠COD-∠BOD-∠COD
=∠DOE-∠BOC
=90°-75°
=15°,
即∠COE-∠BOD=15°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
