浙教版七年级数学每日一题61-65几何新定义问题(含答案)
文档属性
| 名称 | 浙教版七年级数学每日一题61-65几何新定义问题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 23:34:53 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
七年级每日一题61——几何新定义问题探究
班级 姓名 学号
61.对于数轴上给定的两点M,N(M在N的左侧),若数轴上存在点P,使得,则称点P为点M,N的“k和点”.例如,如图1,点M,N表示的数分别为0,2,点P表示的数为1,因为,所以点P是点M,N的“4和点”.
(1)如图2,已知点A表示的数为,点B表示的数为2.
①若点O表示的数为0,点O为点A,B的“k和点”,则k的值______.
②若点C在线段AB上,且点C是点A,B的“5和点”,则点C表示的数为______.
③若点D是点A,B的“k和点”,且,求k的值.
(2) 数轴上点E表示的数为a,点F在点E的右侧,,点T是点E,F的“6和点”,请求出点T表示的数t的值(用含a的代数式表示).
七年级每日一题62——几何新定义问题探究
班级 姓名 学号
62.定义:在数轴上,若C到A的距离刚好是2,则C点叫做A的“喜悦点”;若C到A、B的距离之和为6,则C叫做A、B的“喜悦中心”.
(1)如图1,点A表示的数为-1,则A的喜悦点C所表示的数应该是______;如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为-2,点C是M、N的喜悦中心,则C所表示的所有整数中,整数和是______.
(2)如图3,A、B、P为数轴上三点,点A所表示的数为-1,点B所表示的数为4,点P所表示的数为8,现有一只电子蚂蚁从点P出发,以3个单位每秒的速度向左运动,当经过多少秒时,电子蚂蚁是A和B的喜悦中心?
七年级每日一题63——几何新定义问题探究
班级 姓名 学号
63. 如图(1).点在线段上.图中共有三条线段: 线段, 线段, 线段, 若其中有一条线段的长度是另一条线段长度的两掊, 则称点为线段的 “奇分点”.若,如图(2),点从点开始以每秒3cm的速度向A运动,当点M到达A点时停止运动,运动的时间为t秒.
(1)当t=_____________秒,M是线的“奇分点" (写出一种情况即可)。
(2)如果同时点从点A的位置开始以每秒2cm的速度向点B运动, 如图(3)所示, 井与点同时停止, 则当为几秒时,M是线段AN的“奇分点”?
七年级每日一题64——几何新定义问题探究
班级 姓名 学号
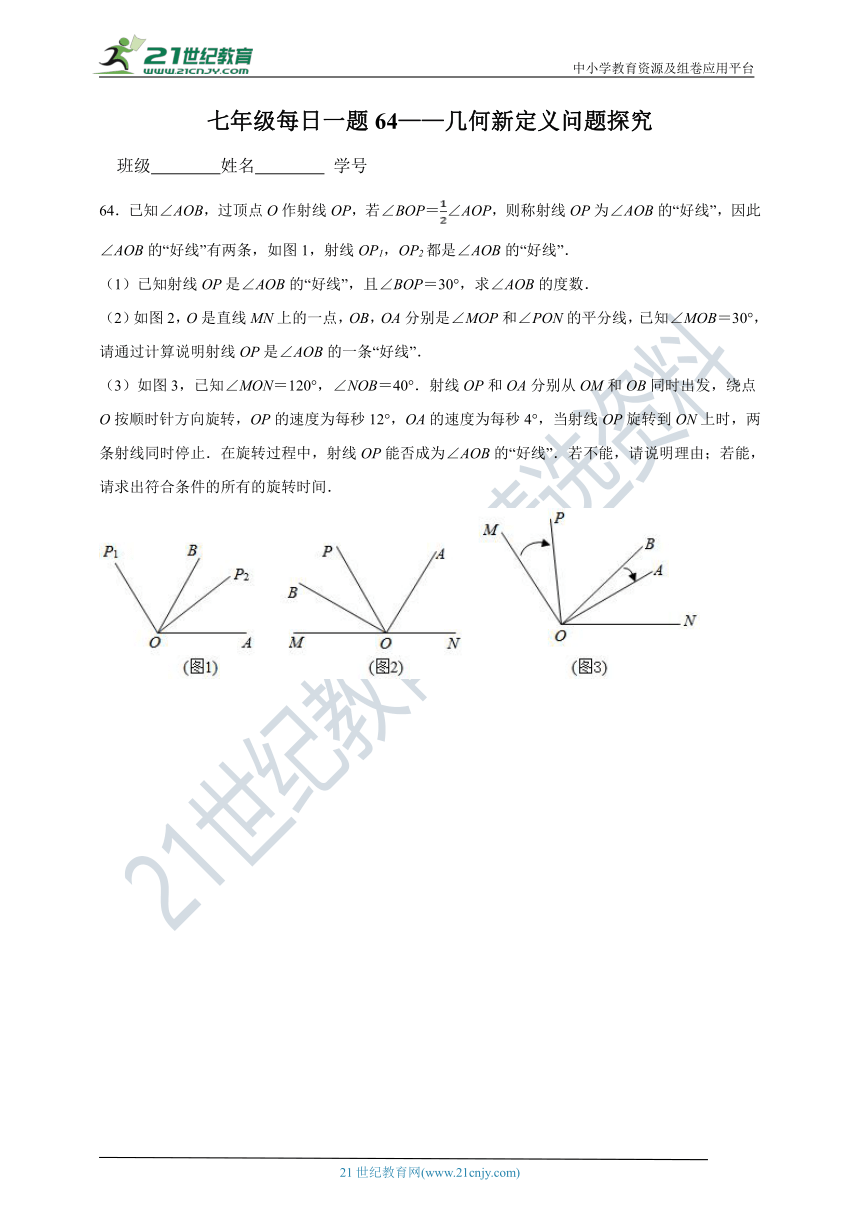
64.已知∠AOB,过顶点O作射线OP,若∠BOP=∠AOP,则称射线OP为∠AOB的“好线”,因此∠AOB的“好线”有两条,如图1,射线OP1,OP2都是∠AOB的“好线”.
(1)已知射线OP是∠AOB的“好线”,且∠BOP=30°,求∠AOB的度数.
(2)如图2,O是直线MN上的一点,OB,OA分别是∠MOP和∠PON的平分线,已知∠MOB=30°,请通过计算说明射线OP是∠AOB的一条“好线”.
(3)如图3,已知∠MON=120°,∠NOB=40°.射线OP和OA分别从OM和OB同时出发,绕点O按顺时针方向旋转,OP的速度为每秒12°,OA的速度为每秒4°,当射线OP旋转到ON上时,两条射线同时停止.在旋转过程中,射线OP能否成为∠AOB的“好线”.若不能,请说明理由;若能,请求出符合条件的所有的旋转时间.
七年级每日一题65——角的旋转探究问题
班级 姓名 学号
65.【概念学习】
点A,B,C为数轴上的三点,如果点C到A的距离是点C到B的距离的2倍,那么我们就称点C是的偶点.
如图1,点A表示的数为,点B表示的数为1,表示0的点C到点A的距离是2,到点B的距离是1,那么点C是的偶点;表示的点D到点A的距离是1,到点B的距离是2,那么点D就不是的偶点,但点D是的偶点.
【初步探究】
已知如图2,M,N为数轴上两点,点M表示的数为,点N表示的数为5,若点F是的偶点,回答下列问题:
(1)当F在点M,N之间,点F表示的数为__________;
(2)当F为数轴上一点,点F表示的数为____________;
【深入思考】
(3)如图3,P、Q为数轴上两点,点P表示的数为,点Q表示的数为40,现有一个动点E从点Q出发,以每秒2个单位的速度向左运动,到达点P停止,若运动时间为t,求当t为何值时,P,Q,E中恰有一个点为其余两点的偶点?
七年级每日一题61—答案
61.(1)解:①∵点O为点A,B的“k和点”,
∴OA+3OB=k,∴点A表示的数为,点B表示的数为2.
∴OA=2,OB=2,∴k=8,故答案为:8;
②设点C表示的数为c,
∵点C是点A,B的“5和点”,∴AC+3BC=5,∴c+2+3(2-c)=5,
解得c=1.5,故答案为:1.5;
③当点D在AB之间,
∵,∴,,
∴;
点D位于点B右侧,
∵,∴,∴,
∴.故k的值为或20;
(2)
解:①当点T位于点E左侧,即时,显然不满足条件.
②当点T在线段EF上时,
∵,
∴.
又∵点T是点E,F的“6和点”,
∴,
∴,,
∴.
③当点T位于点F右侧时,
∵,
∴,
又∵点T是点E,F的“6和点”,
∴,
∴,,
∴,
综上所述,t的值为或.
七年级每日一题62—答案
62.(1)解:当点在点的右边时,
则,
,
点C表示的数是1,
当点在点的左边时,
则,
,
点C表示的数是,
点C表示的数是1或,
点M所表示的数为4,点N所表示的数为-2,
,
设点表示的数为,
点C是M、N的喜悦中心,
只能在之间,
,
则C所表示的所有整数为:
整数和,
故答案为:1或-3;7
(2)解:设经过x秒时,电子蚂蚁是A和B的喜悦中心,依题意有:
①喜悦中心在点B右侧时,8-3x-4+(8-3x+1)=6,
解得x=;
②喜悦中心在点A左侧时,4-(8-3x)+[-1-(8-3x)]=6,
解得x=,
故当经过秒或秒时,电子蚂蚁是A和B的喜悦中心.
七年级每日一题63—答案
【答案】 或或; 或或
【分析】画出图形根据“奇分点”定义列出三个等式即可求解.
【详解】根据题意:,,,
(1)当M是线段的“奇分点"时
①AM=2BM,此时,解得;
②BM=2AM,此时,解得;
③AB=2BM,此时,解得;
∴当M是线段的“奇分点"时,t的值为或或;
(2)∵M是线段AN的“奇分点”.
∴M点在线段AN上,即,
∴,
①AN=2MN,此时M为AN中点,,解得;
②AM =2MN,此时,解得;
③MN=2AM,此时,解得;
∴当M是线的“奇分点"时,t的值为或或;
七年级每日一题64—答案
64.【详解】解:(1)∵射线OP是∠AOB的好线,且∠BOP=30°
∴∠AOP=2∠BOP=60°
∴当OP在∠AOB内部时, ∠AOB =∠BOP +∠AOP =90° ,
当OP在∠AOB外部时,∠AOB = ∠AOP-∠BOP=30°
∴∠AOB =90°或30°;
(2) ∵OB,OA别是∠MOP和∠PON的平分线
∴∠AOB=∠BOP+∠AOP= (∠MOP+∠NOP)=,∠BOP=∠BOM=30°,
∴∠AOP=90°-30°=60°
∴∠BOP=∠AOP
∴OP是∠AOB的一条“好线” ;
(3) 设运动时间为t ,则∠MOP=12t ,∠BOA=4t ,
当OP在OB上方时,∠BOP=80°-12t ,∠AOP=80°+4t-12t=80°-8t ,
∴
解得:t=5;
当OP在OB下方时,∠BOP= 12t-80°, ∠AOP=80°+4t-12t=80°-8t ,
∴,
解得:t=
综上所述:运动时间为5秒或秒.
七年级每日一题65—答案
【详解】(1)解: 设点F表示的数是x,
点F是的偶点,F在点M,N之间,
即,
即点F表示的数是3;
故答案为:3.
(2)解:设点F表示的数是x,依题,得
或
解得:或11;
故答案为:3或11.
(3)解:点E从点Q出发,以每秒2个单位的速度向左运动,到达点P停止,若运动时间为t,则动点E的表示的数为, ,.
分四种情况讨论:
①当点E是的偶点时,,
,
解得:(秒);
②当点E是的偶点时,,
,
解得:(秒);
③当点Q是的偶点时,,
,
解得:(秒);
④点P是的偶点时,,
,
解得:(秒)
综上所述,当为10秒、15秒或20秒时,E、P、Q中恰有一个点为其余两点的偶点.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
七年级每日一题61——几何新定义问题探究
班级 姓名 学号
61.对于数轴上给定的两点M,N(M在N的左侧),若数轴上存在点P,使得,则称点P为点M,N的“k和点”.例如,如图1,点M,N表示的数分别为0,2,点P表示的数为1,因为,所以点P是点M,N的“4和点”.
(1)如图2,已知点A表示的数为,点B表示的数为2.
①若点O表示的数为0,点O为点A,B的“k和点”,则k的值______.
②若点C在线段AB上,且点C是点A,B的“5和点”,则点C表示的数为______.
③若点D是点A,B的“k和点”,且,求k的值.
(2) 数轴上点E表示的数为a,点F在点E的右侧,,点T是点E,F的“6和点”,请求出点T表示的数t的值(用含a的代数式表示).
七年级每日一题62——几何新定义问题探究
班级 姓名 学号
62.定义:在数轴上,若C到A的距离刚好是2,则C点叫做A的“喜悦点”;若C到A、B的距离之和为6,则C叫做A、B的“喜悦中心”.
(1)如图1,点A表示的数为-1,则A的喜悦点C所表示的数应该是______;如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为-2,点C是M、N的喜悦中心,则C所表示的所有整数中,整数和是______.
(2)如图3,A、B、P为数轴上三点,点A所表示的数为-1,点B所表示的数为4,点P所表示的数为8,现有一只电子蚂蚁从点P出发,以3个单位每秒的速度向左运动,当经过多少秒时,电子蚂蚁是A和B的喜悦中心?
七年级每日一题63——几何新定义问题探究
班级 姓名 学号
63. 如图(1).点在线段上.图中共有三条线段: 线段, 线段, 线段, 若其中有一条线段的长度是另一条线段长度的两掊, 则称点为线段的 “奇分点”.若,如图(2),点从点开始以每秒3cm的速度向A运动,当点M到达A点时停止运动,运动的时间为t秒.
(1)当t=_____________秒,M是线的“奇分点" (写出一种情况即可)。
(2)如果同时点从点A的位置开始以每秒2cm的速度向点B运动, 如图(3)所示, 井与点同时停止, 则当为几秒时,M是线段AN的“奇分点”?
七年级每日一题64——几何新定义问题探究
班级 姓名 学号
64.已知∠AOB,过顶点O作射线OP,若∠BOP=∠AOP,则称射线OP为∠AOB的“好线”,因此∠AOB的“好线”有两条,如图1,射线OP1,OP2都是∠AOB的“好线”.
(1)已知射线OP是∠AOB的“好线”,且∠BOP=30°,求∠AOB的度数.
(2)如图2,O是直线MN上的一点,OB,OA分别是∠MOP和∠PON的平分线,已知∠MOB=30°,请通过计算说明射线OP是∠AOB的一条“好线”.
(3)如图3,已知∠MON=120°,∠NOB=40°.射线OP和OA分别从OM和OB同时出发,绕点O按顺时针方向旋转,OP的速度为每秒12°,OA的速度为每秒4°,当射线OP旋转到ON上时,两条射线同时停止.在旋转过程中,射线OP能否成为∠AOB的“好线”.若不能,请说明理由;若能,请求出符合条件的所有的旋转时间.
七年级每日一题65——角的旋转探究问题
班级 姓名 学号
65.【概念学习】
点A,B,C为数轴上的三点,如果点C到A的距离是点C到B的距离的2倍,那么我们就称点C是的偶点.
如图1,点A表示的数为,点B表示的数为1,表示0的点C到点A的距离是2,到点B的距离是1,那么点C是的偶点;表示的点D到点A的距离是1,到点B的距离是2,那么点D就不是的偶点,但点D是的偶点.
【初步探究】
已知如图2,M,N为数轴上两点,点M表示的数为,点N表示的数为5,若点F是的偶点,回答下列问题:
(1)当F在点M,N之间,点F表示的数为__________;
(2)当F为数轴上一点,点F表示的数为____________;
【深入思考】
(3)如图3,P、Q为数轴上两点,点P表示的数为,点Q表示的数为40,现有一个动点E从点Q出发,以每秒2个单位的速度向左运动,到达点P停止,若运动时间为t,求当t为何值时,P,Q,E中恰有一个点为其余两点的偶点?
七年级每日一题61—答案
61.(1)解:①∵点O为点A,B的“k和点”,
∴OA+3OB=k,∴点A表示的数为,点B表示的数为2.
∴OA=2,OB=2,∴k=8,故答案为:8;
②设点C表示的数为c,
∵点C是点A,B的“5和点”,∴AC+3BC=5,∴c+2+3(2-c)=5,
解得c=1.5,故答案为:1.5;
③当点D在AB之间,
∵,∴,,
∴;
点D位于点B右侧,
∵,∴,∴,
∴.故k的值为或20;
(2)
解:①当点T位于点E左侧,即时,显然不满足条件.
②当点T在线段EF上时,
∵,
∴.
又∵点T是点E,F的“6和点”,
∴,
∴,,
∴.
③当点T位于点F右侧时,
∵,
∴,
又∵点T是点E,F的“6和点”,
∴,
∴,,
∴,
综上所述,t的值为或.
七年级每日一题62—答案
62.(1)解:当点在点的右边时,
则,
,
点C表示的数是1,
当点在点的左边时,
则,
,
点C表示的数是,
点C表示的数是1或,
点M所表示的数为4,点N所表示的数为-2,
,
设点表示的数为,
点C是M、N的喜悦中心,
只能在之间,
,
则C所表示的所有整数为:
整数和,
故答案为:1或-3;7
(2)解:设经过x秒时,电子蚂蚁是A和B的喜悦中心,依题意有:
①喜悦中心在点B右侧时,8-3x-4+(8-3x+1)=6,
解得x=;
②喜悦中心在点A左侧时,4-(8-3x)+[-1-(8-3x)]=6,
解得x=,
故当经过秒或秒时,电子蚂蚁是A和B的喜悦中心.
七年级每日一题63—答案
【答案】 或或; 或或
【分析】画出图形根据“奇分点”定义列出三个等式即可求解.
【详解】根据题意:,,,
(1)当M是线段的“奇分点"时
①AM=2BM,此时,解得;
②BM=2AM,此时,解得;
③AB=2BM,此时,解得;
∴当M是线段的“奇分点"时,t的值为或或;
(2)∵M是线段AN的“奇分点”.
∴M点在线段AN上,即,
∴,
①AN=2MN,此时M为AN中点,,解得;
②AM =2MN,此时,解得;
③MN=2AM,此时,解得;
∴当M是线的“奇分点"时,t的值为或或;
七年级每日一题64—答案
64.【详解】解:(1)∵射线OP是∠AOB的好线,且∠BOP=30°
∴∠AOP=2∠BOP=60°
∴当OP在∠AOB内部时, ∠AOB =∠BOP +∠AOP =90° ,
当OP在∠AOB外部时,∠AOB = ∠AOP-∠BOP=30°
∴∠AOB =90°或30°;
(2) ∵OB,OA别是∠MOP和∠PON的平分线
∴∠AOB=∠BOP+∠AOP= (∠MOP+∠NOP)=,∠BOP=∠BOM=30°,
∴∠AOP=90°-30°=60°
∴∠BOP=∠AOP
∴OP是∠AOB的一条“好线” ;
(3) 设运动时间为t ,则∠MOP=12t ,∠BOA=4t ,
当OP在OB上方时,∠BOP=80°-12t ,∠AOP=80°+4t-12t=80°-8t ,
∴
解得:t=5;
当OP在OB下方时,∠BOP= 12t-80°, ∠AOP=80°+4t-12t=80°-8t ,
∴,
解得:t=
综上所述:运动时间为5秒或秒.
七年级每日一题65—答案
【详解】(1)解: 设点F表示的数是x,
点F是的偶点,F在点M,N之间,
即,
即点F表示的数是3;
故答案为:3.
(2)解:设点F表示的数是x,依题,得
或
解得:或11;
故答案为:3或11.
(3)解:点E从点Q出发,以每秒2个单位的速度向左运动,到达点P停止,若运动时间为t,则动点E的表示的数为, ,.
分四种情况讨论:
①当点E是的偶点时,,
,
解得:(秒);
②当点E是的偶点时,,
,
解得:(秒);
③当点Q是的偶点时,,
,
解得:(秒);
④点P是的偶点时,,
,
解得:(秒)
综上所述,当为10秒、15秒或20秒时,E、P、Q中恰有一个点为其余两点的偶点.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
