2023—2024学年浙教版数学九年级上册周测十(3.8)(含答案)
文档属性
| 名称 | 2023—2024学年浙教版数学九年级上册周测十(3.8)(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 825.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-14 15:12:47 | ||
图片预览




文档简介
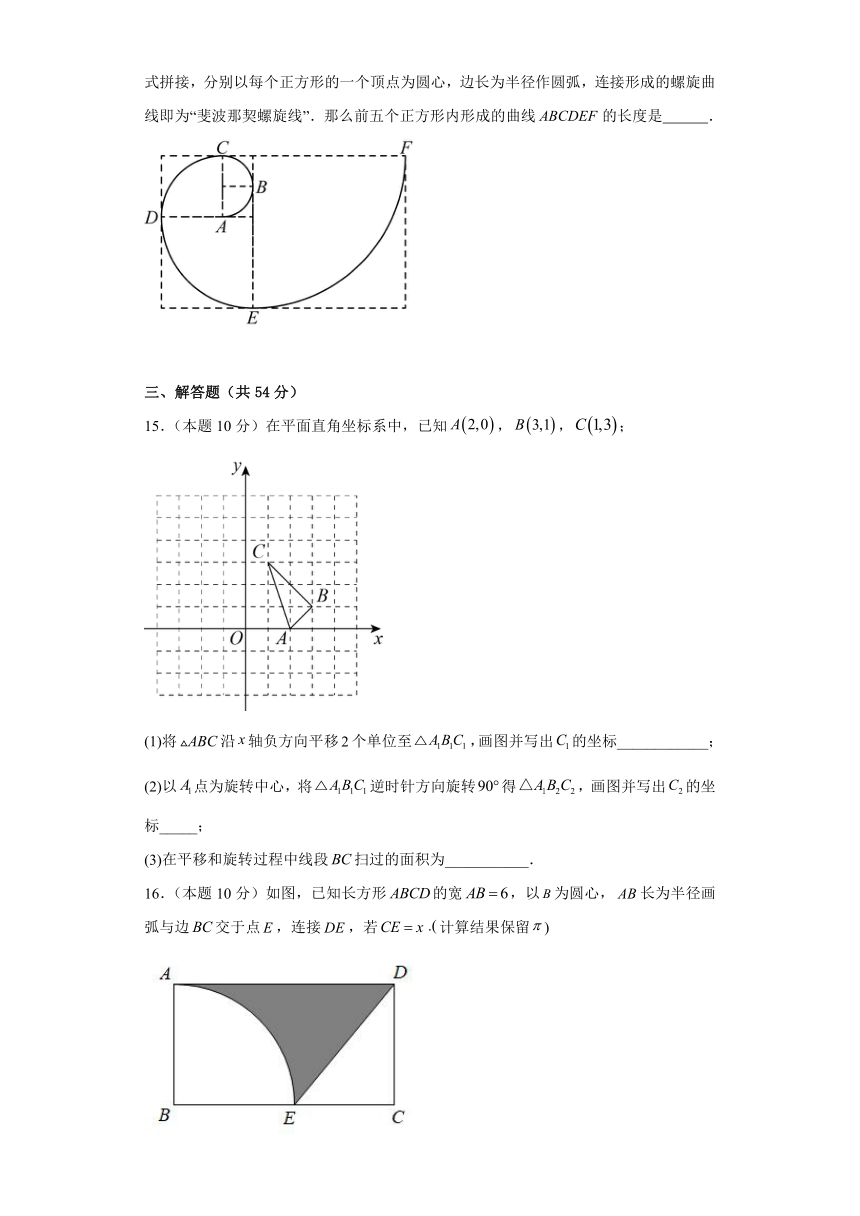
2023-2024学年度第一学期九年级数学(浙教版)周测十(3.8)
学校:___________姓名:___________班级:___________考号:___________
一、单选题(共30分)
1.(本题3分)已知圆锥的底面半径为,母线长为,则其侧面积为 ( )
A. B. C. D.
2.(本题3分)如图是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图2所示,它是以为圆心.,长分别为半径,圆心角形成的扇面,若,,则阴影部分的面积是( )
A. B. C. D.
3.(本题3分)如图,两个大小一样的传送轮连接着一条传送带,则这条传送带的长为( )
A. B. C. D.
4.(本题3分)一个扇形的半径为6,弧长等于,则扇形的圆心角度数为( )
A. B. C. D.
5.(本题3分)如图,在中,,,,以点B为圆心,长为半径画弧,交于点D,图中阴影部分的面积是( )
A. B. C. D.
6.(本题3分)如图,有一块长为、宽为的矩形木板在桌面上按顺时针方向无滑动地翻滚,木板上顶点的位置变化为,其中,第二次翻滚时被桌面上一个小木块挡住,使木板边沿与桌面成角,则点翻滚到点的位置经过的路径长为( )
A. B. C. D.
7.(本题3分)如图,是的直径,,则( )
A. B. C. D.
8.(本题3分)如图在中,,以为直径作半圆,形成了3部分封闭且不重合的图形,其中两部分面积分别为和.则和的关系为( )
A. B. C. D.不能确定
9.(本题3分)从两张同样大小的正方形铁皮上分别剪下不同规格的圆片(如图),剩下的废料相比较,( )
A.剪法1比较多 B.剪法2比较多 C.两种剪法同样多 D.无法比较
10.(本题3分)如图,在中,,,,将绕点顺时针旋转后得到,点经过的路径为,将线段绕点顺时针旋转后,点恰好落在上的点处,点经过的路径为,则图中阴影部分的面积是( )
A. B. C. D.
二、填空题(共16分)
11.(本题4分)扇形的半径为,面积为,则该扇形的圆心角为 .
12.(本题4分)如图,用一个半径为10cm的定滑轮带动重物上升,滑轮上一点P旋转了,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了 cm.
13.(本题4分)如图.在边长为2的正方形中,对角线、交于点O,分别以点A、B、C、D为圆心,为半径画弧,弧分别与边、、、交于点E、F、G、H,则阴影部分的面积为 .
14.(本题4分)“斐波那契螺旋线”(也称“黄金螺旋”)是根据斐波那契数列画出来的螺旋曲线,人类耳朵的形状也符合这种螺旋形状,这种形状的构造帮助人类可以更好地接收声波,从而增强听觉.现依次取边长为1,1,2,3,5……的正方形按如图所示方式拼接,分别以每个正方形的一个顶点为圆心,边长为半径作圆弧,连接形成的螺旋曲线即为“斐波那契螺旋线”.那么前五个正方形内形成的曲线的长度是 .
三、解答题(共54分)
15.(本题10分)在平面直角坐标系中,已知,,;
(1)将沿轴负方向平移个单位至,画图并写出的坐标____________;
(2)以点为旋转中心,将逆时针方向旋转得,画图并写出的坐标_____;
(3)在平移和旋转过程中线段扫过的面积为___________.
16.(本题10分)如图,已知长方形的宽,以为圆心,长为半径画弧与边交于点,连接,若计算结果保留)
(1)用含的代数式表示图中阴影部分的面积;
(2)当时,求图中阴影部分的面积.
17.(本题10分)如图,四边形内接于,且的半径为r,.
(1)若,求的长.
(2)若,求证:.
18.(本题12分)如图,在中,弦,相交于点E,连结,已知.
(1)求证:;
(2)连结、,若,的半径为2,求的长.
19.(本题12分)如图①,矩形与以为直径的半圆在直线的上方,线段与点、都在直线上,且,,.点以个单位/秒的速度从点处出发,沿射线方向运动,矩形随之运动,运动时间为秒.
(1)如图②,当时,求半圆在矩形内的弧的长度;
(2)在点运动的过程中,当、都与半圆相交时,设这两个交点为、.连接、,若为直角,求此时的值.
参考答案:
1.D
2.C
3.B
4.C
5.A
6.B
7.D
8.B
9.C
10.A
11./60度
12.
13.
14.
15.(1)解:如图所示:即为所求,,
故答案为:;
(2)如图所示:即为所求,,
故答案为:;
(3)根据题意,每个小正方形的边长为,
∴,
,
∵将沿轴负方向平移个单位至,
∴,,
∴四边形是平行四边形,
∴在平移和旋转过程中线段扫过的面积为: ,
故答案为:.
16.(1)解:设,,
∴,
∴
,即阴影部分的面积是.
(2)解:由(1)可知,,
∴,
即时,阴影部分的面积是.
17.(1)解:连接,,,
四边形内接于,,
,
,
的长为;
(2)证明:,
,
,
,
,
,
,
为等边三角形,
.
18.(1)证:∵,
∴,
∴,
∴,
∴;
(2)解:∵,
∴,
∴,
∴,
∵的半径为2,
∴.
19.(1)解:设与交于点,连接,
当时,,
∵,
∴,
∴,
∴,
在矩形中,,
∴,
又∵,
∴,
∴是等边三角形,
∴,
∴,
即半圆在矩形内的弧的长度为;
(2)连接,,
∵,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∵,
∴,
∴,
在中,,
∴,
解得:,,
即的值为18或16.
学校:___________姓名:___________班级:___________考号:___________
一、单选题(共30分)
1.(本题3分)已知圆锥的底面半径为,母线长为,则其侧面积为 ( )
A. B. C. D.
2.(本题3分)如图是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图2所示,它是以为圆心.,长分别为半径,圆心角形成的扇面,若,,则阴影部分的面积是( )
A. B. C. D.
3.(本题3分)如图,两个大小一样的传送轮连接着一条传送带,则这条传送带的长为( )
A. B. C. D.
4.(本题3分)一个扇形的半径为6,弧长等于,则扇形的圆心角度数为( )
A. B. C. D.
5.(本题3分)如图,在中,,,,以点B为圆心,长为半径画弧,交于点D,图中阴影部分的面积是( )
A. B. C. D.
6.(本题3分)如图,有一块长为、宽为的矩形木板在桌面上按顺时针方向无滑动地翻滚,木板上顶点的位置变化为,其中,第二次翻滚时被桌面上一个小木块挡住,使木板边沿与桌面成角,则点翻滚到点的位置经过的路径长为( )
A. B. C. D.
7.(本题3分)如图,是的直径,,则( )
A. B. C. D.
8.(本题3分)如图在中,,以为直径作半圆,形成了3部分封闭且不重合的图形,其中两部分面积分别为和.则和的关系为( )
A. B. C. D.不能确定
9.(本题3分)从两张同样大小的正方形铁皮上分别剪下不同规格的圆片(如图),剩下的废料相比较,( )
A.剪法1比较多 B.剪法2比较多 C.两种剪法同样多 D.无法比较
10.(本题3分)如图,在中,,,,将绕点顺时针旋转后得到,点经过的路径为,将线段绕点顺时针旋转后,点恰好落在上的点处,点经过的路径为,则图中阴影部分的面积是( )
A. B. C. D.
二、填空题(共16分)
11.(本题4分)扇形的半径为,面积为,则该扇形的圆心角为 .
12.(本题4分)如图,用一个半径为10cm的定滑轮带动重物上升,滑轮上一点P旋转了,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了 cm.
13.(本题4分)如图.在边长为2的正方形中,对角线、交于点O,分别以点A、B、C、D为圆心,为半径画弧,弧分别与边、、、交于点E、F、G、H,则阴影部分的面积为 .
14.(本题4分)“斐波那契螺旋线”(也称“黄金螺旋”)是根据斐波那契数列画出来的螺旋曲线,人类耳朵的形状也符合这种螺旋形状,这种形状的构造帮助人类可以更好地接收声波,从而增强听觉.现依次取边长为1,1,2,3,5……的正方形按如图所示方式拼接,分别以每个正方形的一个顶点为圆心,边长为半径作圆弧,连接形成的螺旋曲线即为“斐波那契螺旋线”.那么前五个正方形内形成的曲线的长度是 .
三、解答题(共54分)
15.(本题10分)在平面直角坐标系中,已知,,;
(1)将沿轴负方向平移个单位至,画图并写出的坐标____________;
(2)以点为旋转中心,将逆时针方向旋转得,画图并写出的坐标_____;
(3)在平移和旋转过程中线段扫过的面积为___________.
16.(本题10分)如图,已知长方形的宽,以为圆心,长为半径画弧与边交于点,连接,若计算结果保留)
(1)用含的代数式表示图中阴影部分的面积;
(2)当时,求图中阴影部分的面积.
17.(本题10分)如图,四边形内接于,且的半径为r,.
(1)若,求的长.
(2)若,求证:.
18.(本题12分)如图,在中,弦,相交于点E,连结,已知.
(1)求证:;
(2)连结、,若,的半径为2,求的长.
19.(本题12分)如图①,矩形与以为直径的半圆在直线的上方,线段与点、都在直线上,且,,.点以个单位/秒的速度从点处出发,沿射线方向运动,矩形随之运动,运动时间为秒.
(1)如图②,当时,求半圆在矩形内的弧的长度;
(2)在点运动的过程中,当、都与半圆相交时,设这两个交点为、.连接、,若为直角,求此时的值.
参考答案:
1.D
2.C
3.B
4.C
5.A
6.B
7.D
8.B
9.C
10.A
11./60度
12.
13.
14.
15.(1)解:如图所示:即为所求,,
故答案为:;
(2)如图所示:即为所求,,
故答案为:;
(3)根据题意,每个小正方形的边长为,
∴,
,
∵将沿轴负方向平移个单位至,
∴,,
∴四边形是平行四边形,
∴在平移和旋转过程中线段扫过的面积为: ,
故答案为:.
16.(1)解:设,,
∴,
∴
,即阴影部分的面积是.
(2)解:由(1)可知,,
∴,
即时,阴影部分的面积是.
17.(1)解:连接,,,
四边形内接于,,
,
,
的长为;
(2)证明:,
,
,
,
,
,
,
为等边三角形,
.
18.(1)证:∵,
∴,
∴,
∴,
∴;
(2)解:∵,
∴,
∴,
∴,
∵的半径为2,
∴.
19.(1)解:设与交于点,连接,
当时,,
∵,
∴,
∴,
∴,
在矩形中,,
∴,
又∵,
∴,
∴是等边三角形,
∴,
∴,
即半圆在矩形内的弧的长度为;
(2)连接,,
∵,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∵,
∴,
∴,
在中,,
∴,
解得:,,
即的值为18或16.
同课章节目录
