2023—2024学年浙教版数学九年级上册周测七(3.2-3.3)(含答案)
文档属性
| 名称 | 2023—2024学年浙教版数学九年级上册周测七(3.2-3.3)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 916.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-14 15:16:13 | ||
图片预览




文档简介
2023-2024学年度第一学期九年级数学(浙教版)周测七(3.2-3.3)
学校:___________姓名:___________班级:___________考号:___________
一、单选题(共30分)
1.(本题3分)如图,将绕点按逆时针方向旋转后得到,若,则的度数是( )
A. B. C. D.
2.(本题3分)如图,是由旋转后得到的,下列说法正确的是( )
A.旋转中心不是点 B.
C.旋转方向是顺时针 D.
3.(本题3分)如图,线段是的直径,于点E,若长为16,长为6,则半径是( )
A.5 B.6 C.8 D.10
4.(本题3分)下列说法正确的是( )
A.角平分线上的点到角两边的距离相等
B.平行四边形既是轴对称图形,又是中心对称图形
C.平分弦的直径垂直于这条弦
D.经过平面内点可以作一个圆
5.(本题3分)如图,在平面直角坐标系中,已知线段在y轴上,点,原点O是线段的中点,将线段绕点O逆时针旋转得到线段,连接形成四边形,分别交x轴于E、F两点,则四边形的面积为( )
A.4 B. C. D.
6.(本题3分)如图,在中,,将绕点逆时针旋转得到,点的对应点为点,若点,,恰好在同一条直线上,则的度数为( )
A. B. C. D.
7.(本题3分)如图,点是上两点,,点P是上的动点(P与不重合),连接,过点O分别作交于点E,交于点F,则等于( )
A.2 B.3 C.5 D.6
8.(本题3分)如图,已知的直径为26,弦,动点在上,弦,若点分别是弦的中点,则线段的取值范围是( )
A. B. C. D.
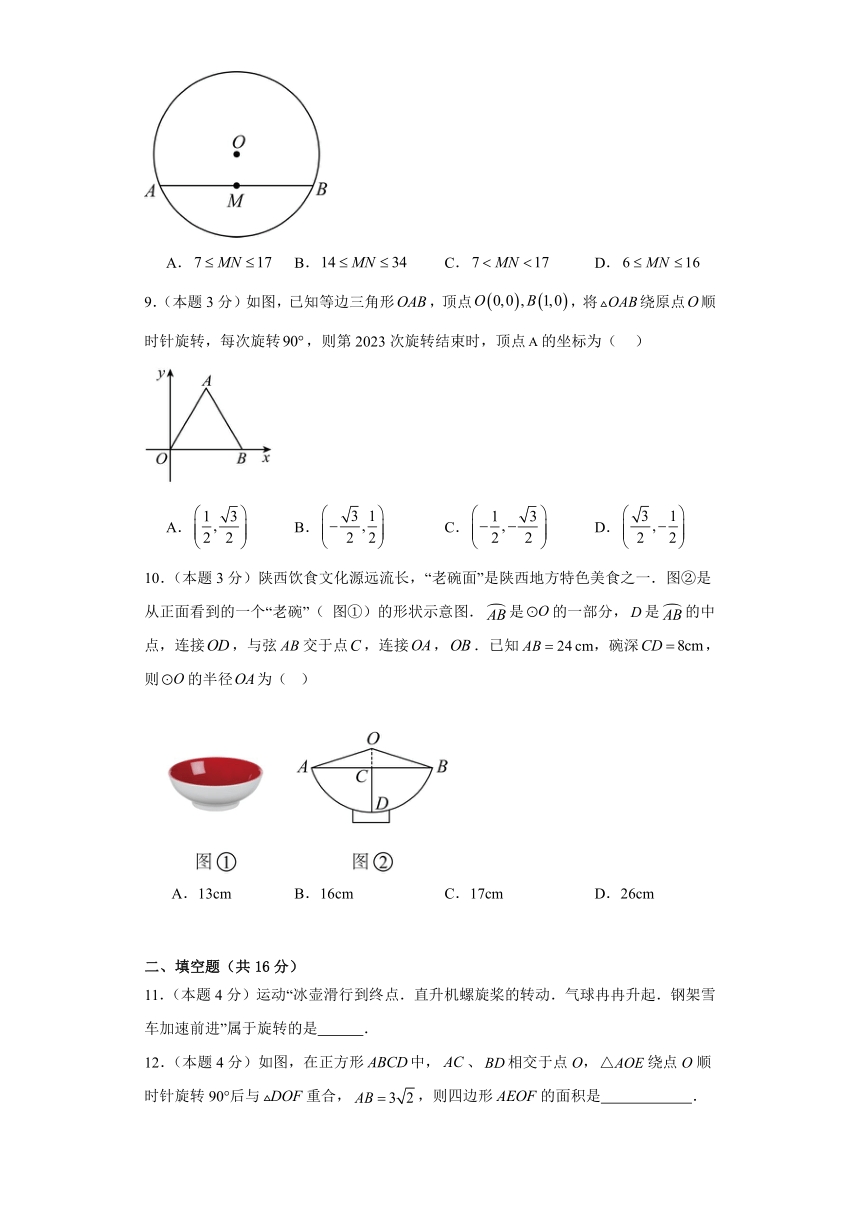
9.(本题3分)如图,已知等边三角形,顶点,将绕原点顺时针旋转,每次旋转,则第2023次旋转结束时,顶点的坐标为( )
A. B. C. D.
10.(本题3分)陕西饮食文化源远流长,“老碗面”是陕西地方特色美食之一.图②是从正面看到的一个“老碗”( 图①)的形状示意图.是的一部分,是的中点,连接,与弦交于点,连接,.已知cm,碗深,则的半径为( )
A.13cm B.16cm C.17cm D.26cm
二、填空题(共16分)
11.(本题4分)运动“冰壶滑行到终点.直升机螺旋桨的转动.气球冉冉升起.钢架雪车加速前进”属于旋转的是 .
12.(本题4分)如图,在正方形中,、相交于点O,绕点O顺时针旋转90°后与重合,,则四边形的面积是 .
13.(本题4分)如图,是的直径,弦,垂足为,连接,若,,则弦的长为 .
14.(本题4分)《九章算术》是我国古代著名数学著作,书中记载:“今有圆材,埋在壁中,不知大小以锯锯之,深一寸,锯道长一尺,问径几何?”用数学语言可表述为:“如图,为的直径,弦于,寸,寸,求直径的长.”则 寸.
三、解答题(共54分)
15.(本题10分)利用图中的网格线(最小的正方形的边长为1)画图.
(1)作出关于原点对称的中心对称图形.
(2)将绕点顺时针能转得到.
16.(本题10分)如图1是博物馆展出的古代车轮实物,《周礼·考工记》记载:“……故兵车之轮六尺有六寸,田车之轮六尺有三寸……”据此,我们可以通过计算车轮的半径来验证车轮类型,请将以下推理过程补充完整.
如图2所示,在车轮上取A,B两点,设所在圆的圆心为O,半径为.
作弦AB的垂线OC,D为垂足,则___________.
经测量,,则___________;用含r的代数式表示___________.
在中,由勾股定理可列出关于r的方程:___________.解得.
通过换算,车轮直径约为六尺六寸,可验证此车轮为___________之轮.(填“兵车”或“田车”)
17.(本题10分)如图,在中,,,,逆时针旋转一定角度后与重合,且点C恰好成为的中点.
(1)旋转中心为点 ,并求出旋转角= 度;
(2)求出的度数和的长.
18.(本题12分)筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2,已知圆心O在水面上方,且⊙O被水面截得的弦为6米,⊙O半径长为4米.若点C为运行轨道的最低点,求点C到弦所在直线的距离.
19.(本题12分)如图,有两条公路相交成角,沿公路方向离点160米处有一所学校,当重型运输卡车沿道路方向行驶时,在以为圆心,100米为半径的圆形区域内都会受到卡车噪声的影响,且卡车与学校的距离越近噪声影响越大.若已知重型运输卡车沿道路方向行驶的速度为36千米/时.
(1)求对学校的噪声影响最大时卡车与学校的距离是多少米?
(2)重型运输卡车沿道路方向行驶一次给学校带来噪声影响的时间是多少秒?
参考答案:
1.A
2.D
3.D
4.A
5.B
6.C
7.C
8.A
9.B
10.A
11.直升机螺旋桨的转动
12.
13.
14.26
15.(1)如图:即为所求
(2)如图;即为所求
16.解:根据垂直弦的直径平分弦可知:,
∵,
∴,,
∴,
解得:,
∴此车轮为:兵车之轮;
故答案为:,,,,兵车.
17.(1)解:,
即,
逆时针旋转一定角度后与重合,
∴旋转中心为点A,旋转的度数为130;
故答案为:A;130
(2)解:逆时针旋转一定角度后与重合,
,,,
,
∵点C恰好成为AD的中点,
,
.
18.解:如图2,连接交于,连接,
点为运行轨道的最低点,
,米,
(米,
在中,(米,
点到弦所在直线的距离米,
点C到弦所在直线的距离为米.
19.(1)解:如图,作于,
,,
,
即对学校的噪声影响最大时卡车与学校的距离m;
(2)解:如图,以为圆心m为半径画圆,交于、两点,连接,
,
,,
,
在中,m,
m,
重型运输卡车的速度为36千米时米秒,
重型运输卡车经过的时间(秒,
故卡车沿道路方向行驶一次给学校带来噪声影响的时间为12秒.
学校:___________姓名:___________班级:___________考号:___________
一、单选题(共30分)
1.(本题3分)如图,将绕点按逆时针方向旋转后得到,若,则的度数是( )
A. B. C. D.
2.(本题3分)如图,是由旋转后得到的,下列说法正确的是( )
A.旋转中心不是点 B.
C.旋转方向是顺时针 D.
3.(本题3分)如图,线段是的直径,于点E,若长为16,长为6,则半径是( )
A.5 B.6 C.8 D.10
4.(本题3分)下列说法正确的是( )
A.角平分线上的点到角两边的距离相等
B.平行四边形既是轴对称图形,又是中心对称图形
C.平分弦的直径垂直于这条弦
D.经过平面内点可以作一个圆
5.(本题3分)如图,在平面直角坐标系中,已知线段在y轴上,点,原点O是线段的中点,将线段绕点O逆时针旋转得到线段,连接形成四边形,分别交x轴于E、F两点,则四边形的面积为( )
A.4 B. C. D.
6.(本题3分)如图,在中,,将绕点逆时针旋转得到,点的对应点为点,若点,,恰好在同一条直线上,则的度数为( )
A. B. C. D.
7.(本题3分)如图,点是上两点,,点P是上的动点(P与不重合),连接,过点O分别作交于点E,交于点F,则等于( )
A.2 B.3 C.5 D.6
8.(本题3分)如图,已知的直径为26,弦,动点在上,弦,若点分别是弦的中点,则线段的取值范围是( )
A. B. C. D.
9.(本题3分)如图,已知等边三角形,顶点,将绕原点顺时针旋转,每次旋转,则第2023次旋转结束时,顶点的坐标为( )
A. B. C. D.
10.(本题3分)陕西饮食文化源远流长,“老碗面”是陕西地方特色美食之一.图②是从正面看到的一个“老碗”( 图①)的形状示意图.是的一部分,是的中点,连接,与弦交于点,连接,.已知cm,碗深,则的半径为( )
A.13cm B.16cm C.17cm D.26cm
二、填空题(共16分)
11.(本题4分)运动“冰壶滑行到终点.直升机螺旋桨的转动.气球冉冉升起.钢架雪车加速前进”属于旋转的是 .
12.(本题4分)如图,在正方形中,、相交于点O,绕点O顺时针旋转90°后与重合,,则四边形的面积是 .
13.(本题4分)如图,是的直径,弦,垂足为,连接,若,,则弦的长为 .
14.(本题4分)《九章算术》是我国古代著名数学著作,书中记载:“今有圆材,埋在壁中,不知大小以锯锯之,深一寸,锯道长一尺,问径几何?”用数学语言可表述为:“如图,为的直径,弦于,寸,寸,求直径的长.”则 寸.
三、解答题(共54分)
15.(本题10分)利用图中的网格线(最小的正方形的边长为1)画图.
(1)作出关于原点对称的中心对称图形.
(2)将绕点顺时针能转得到.
16.(本题10分)如图1是博物馆展出的古代车轮实物,《周礼·考工记》记载:“……故兵车之轮六尺有六寸,田车之轮六尺有三寸……”据此,我们可以通过计算车轮的半径来验证车轮类型,请将以下推理过程补充完整.
如图2所示,在车轮上取A,B两点,设所在圆的圆心为O,半径为.
作弦AB的垂线OC,D为垂足,则___________.
经测量,,则___________;用含r的代数式表示___________.
在中,由勾股定理可列出关于r的方程:___________.解得.
通过换算,车轮直径约为六尺六寸,可验证此车轮为___________之轮.(填“兵车”或“田车”)
17.(本题10分)如图,在中,,,,逆时针旋转一定角度后与重合,且点C恰好成为的中点.
(1)旋转中心为点 ,并求出旋转角= 度;
(2)求出的度数和的长.
18.(本题12分)筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2,已知圆心O在水面上方,且⊙O被水面截得的弦为6米,⊙O半径长为4米.若点C为运行轨道的最低点,求点C到弦所在直线的距离.
19.(本题12分)如图,有两条公路相交成角,沿公路方向离点160米处有一所学校,当重型运输卡车沿道路方向行驶时,在以为圆心,100米为半径的圆形区域内都会受到卡车噪声的影响,且卡车与学校的距离越近噪声影响越大.若已知重型运输卡车沿道路方向行驶的速度为36千米/时.
(1)求对学校的噪声影响最大时卡车与学校的距离是多少米?
(2)重型运输卡车沿道路方向行驶一次给学校带来噪声影响的时间是多少秒?
参考答案:
1.A
2.D
3.D
4.A
5.B
6.C
7.C
8.A
9.B
10.A
11.直升机螺旋桨的转动
12.
13.
14.26
15.(1)如图:即为所求
(2)如图;即为所求
16.解:根据垂直弦的直径平分弦可知:,
∵,
∴,,
∴,
解得:,
∴此车轮为:兵车之轮;
故答案为:,,,,兵车.
17.(1)解:,
即,
逆时针旋转一定角度后与重合,
∴旋转中心为点A,旋转的度数为130;
故答案为:A;130
(2)解:逆时针旋转一定角度后与重合,
,,,
,
∵点C恰好成为AD的中点,
,
.
18.解:如图2,连接交于,连接,
点为运行轨道的最低点,
,米,
(米,
在中,(米,
点到弦所在直线的距离米,
点C到弦所在直线的距离为米.
19.(1)解:如图,作于,
,,
,
即对学校的噪声影响最大时卡车与学校的距离m;
(2)解:如图,以为圆心m为半径画圆,交于、两点,连接,
,
,,
,
在中,m,
m,
重型运输卡车的速度为36千米时米秒,
重型运输卡车经过的时间(秒,
故卡车沿道路方向行驶一次给学校带来噪声影响的时间为12秒.
同课章节目录
