4.2 由平行线截得的比例线段 课件(29张ppt)
文档属性
| 名称 | 4.2 由平行线截得的比例线段 课件(29张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 23:49:19 | ||
图片预览








文档简介
(共29张PPT)
浙教版九年级上册
4.2 由平行线截得的比例线段
第四章 相似三角形
1.观察有横格线的练习簿页(如图),这些横格线有什么特征 在图中任意画几条直线,使之与横格线相交.这些横格线在每一条所画的直线上截得的线段有什么规律
┍
A
B
┍
C
D
┍
E
F
┍
G
H
AB=CD=EF=GH
等距:
等分线段:
┍
A
B
┍
C
D
┍
E
F
┍
G
H
K
AC=CE=EG=GK
┍
A
B
┍
C
D
┍
E
F
┍
G
H
K
△ABC≌△CDE≌△EFG≌△GHK (AAS)
结论:等距的一组平行线等分线段
温故知新:
结论:等距的一组平行线等分线段
l1
l2
l3
l4
l5
A
B
C
D
E
A1
B1
C1
D1
E1
写出含AB的几组比例线段:
.
.
.
.
.
.
…………
l1
l2
l3
l4
l5
l1
l4
l5
A
B
C
D
E
A1
B1
C1
D1
E1
l1
l3
l4
l5
A
C
D
E
A1
C1
D1
E1
A
D
E
A1
D1
E1
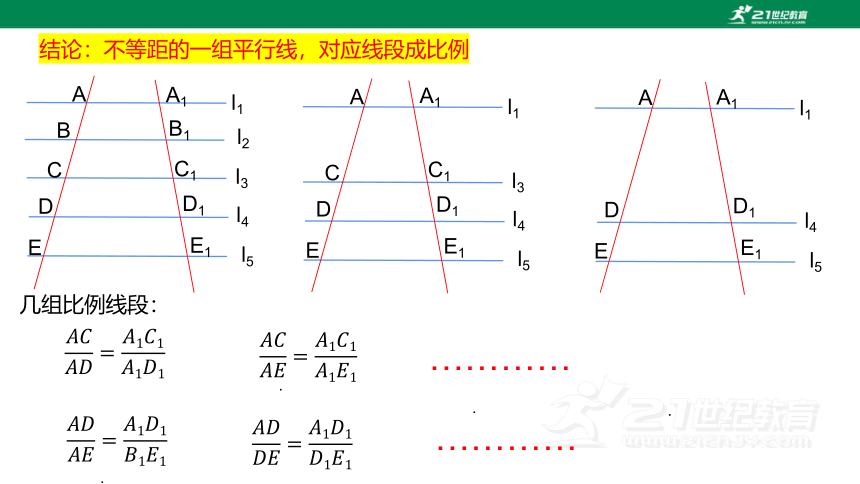
几组比例线段:
.
.
.
.
.
…………
…………
结论:不等距的一组平行线,对应线段成比例
D
E
F
S3
S4
平行线分线段成比例定理:
两条直线被一组平行线(不少于3条)所截,
所得的对应线段成比例.
∵ L1//L2//L3
(平行线分线段成比例定理)
几何语言
.
L1
L2
L3
a
b
L1
L2
L3
a
b
L1
L2
L3
a
b
L1
L2
L3
a
b
A
B
C
D
E
A
B
C
D
E
A字形:
.
.
L1
L2
L3
a
b
L1
L2
L3
a
b
a
b
L1
L2
L3
E
A
B
D
C
E
A
B
D
C
“8”字型:
.
.
推论:
平行于三角形一边的直线
截其他两边(或两边的延长线),
所得的对应线段成比例。
数学符号语言:
∵ DE∥BC
AD AE
AB AC
∴
——
——
=
A
B
C
D
E
A
B
C
E
D
.
平行线分线段成比例的基本事实的常见变形(如图):
例1 如图,直线l1 // l2 // l3 ,直线AC分别交l1, l2, l3 ,与点A,B,C;直线DF分别交l1, l2, l3 ,与点D,E,F;已知DE=3,EF=6,AB=4,求AC的长.
A
B
C
D
E
F
l1
l2
l3
解:∵ l1//l2//l3 ,
学以致用
例2 已知:线段AB
求作:线段AB的五等分点.
作法:1)作射线AC.
2)在射线AC上顺次截取
AD=DE=EF=FG=GH.
3)连结HB.
4)过点G、F、E、D分别作HB的平行线GL、FK、 EJ、DI,分别交AB于点L、K、J、I.
L、K、J、I就是所求的五等分点
A
B
C
F
D
E
G
H
I
J
K
L
B
夯实基础,稳扎稳打
.
.
EC=8
.
2、
如图:DE∥BC,
已知:
2
=
——
AE
AC
—
5
=
——
AD
AB
则:
——
A
B
C
E
D
2
—
5
.
C
.
5.如图,已知在△ABC中,点D,E,F分别是边AB,AC,BC上的点, DE∥BC,EF∥AB,且AD∶DB=3∶5,那么CF∶CB等于 ( )
A.5∶8 B.3∶8
C.3∶5 D.2∶5
A
A
B
C
D
E
——
——
6、判断题:
如图:DE∥BC, 下列各式是否正确
D:
——
——
=
AD
AE
AB
AC
( )
C:
——
——
=
AD
AC
AE
AB
( )
B:
——
——
=
AD
BD
AE
CE
( )
A:
AD
AB
=
AE
AC
( )
√
√
√
×
7.如图,已知l1∥l2∥l3,AM=3 cm,BM=5 cm,CM=4.5 cm,EF=12 cm,则DM=____cm,EK=____cm,FK=____cm.
7.5
4.5
7.5
F
BF=DE
DE
8.
DBFE
连续递推,豁然开朗
9.如图所示,在△ABC中,DE∥BC,EF∥DC.
求证:AD2=AB·AF.
证明:∵DE∥BC,∴AD∶AB=AE∶AC.
∵EF∥DC,∴AF∶AD=AE∶AC,
∴AD∶AB=AF∶AD,∴AD2=AB·AF.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
浙教版九年级上册
4.2 由平行线截得的比例线段
第四章 相似三角形
1.观察有横格线的练习簿页(如图),这些横格线有什么特征 在图中任意画几条直线,使之与横格线相交.这些横格线在每一条所画的直线上截得的线段有什么规律
┍
A
B
┍
C
D
┍
E
F
┍
G
H
AB=CD=EF=GH
等距:
等分线段:
┍
A
B
┍
C
D
┍
E
F
┍
G
H
K
AC=CE=EG=GK
┍
A
B
┍
C
D
┍
E
F
┍
G
H
K
△ABC≌△CDE≌△EFG≌△GHK (AAS)
结论:等距的一组平行线等分线段
温故知新:
结论:等距的一组平行线等分线段
l1
l2
l3
l4
l5
A
B
C
D
E
A1
B1
C1
D1
E1
写出含AB的几组比例线段:
.
.
.
.
.
.
…………
l1
l2
l3
l4
l5
l1
l4
l5
A
B
C
D
E
A1
B1
C1
D1
E1
l1
l3
l4
l5
A
C
D
E
A1
C1
D1
E1
A
D
E
A1
D1
E1
几组比例线段:
.
.
.
.
.
…………
…………
结论:不等距的一组平行线,对应线段成比例
D
E
F
S3
S4
平行线分线段成比例定理:
两条直线被一组平行线(不少于3条)所截,
所得的对应线段成比例.
∵ L1//L2//L3
(平行线分线段成比例定理)
几何语言
.
L1
L2
L3
a
b
L1
L2
L3
a
b
L1
L2
L3
a
b
L1
L2
L3
a
b
A
B
C
D
E
A
B
C
D
E
A字形:
.
.
L1
L2
L3
a
b
L1
L2
L3
a
b
a
b
L1
L2
L3
E
A
B
D
C
E
A
B
D
C
“8”字型:
.
.
推论:
平行于三角形一边的直线
截其他两边(或两边的延长线),
所得的对应线段成比例。
数学符号语言:
∵ DE∥BC
AD AE
AB AC
∴
——
——
=
A
B
C
D
E
A
B
C
E
D
.
平行线分线段成比例的基本事实的常见变形(如图):
例1 如图,直线l1 // l2 // l3 ,直线AC分别交l1, l2, l3 ,与点A,B,C;直线DF分别交l1, l2, l3 ,与点D,E,F;已知DE=3,EF=6,AB=4,求AC的长.
A
B
C
D
E
F
l1
l2
l3
解:∵ l1//l2//l3 ,
学以致用
例2 已知:线段AB
求作:线段AB的五等分点.
作法:1)作射线AC.
2)在射线AC上顺次截取
AD=DE=EF=FG=GH.
3)连结HB.
4)过点G、F、E、D分别作HB的平行线GL、FK、 EJ、DI,分别交AB于点L、K、J、I.
L、K、J、I就是所求的五等分点
A
B
C
F
D
E
G
H
I
J
K
L
B
夯实基础,稳扎稳打
.
.
EC=8
.
2、
如图:DE∥BC,
已知:
2
=
——
AE
AC
—
5
=
——
AD
AB
则:
——
A
B
C
E
D
2
—
5
.
C
.
5.如图,已知在△ABC中,点D,E,F分别是边AB,AC,BC上的点, DE∥BC,EF∥AB,且AD∶DB=3∶5,那么CF∶CB等于 ( )
A.5∶8 B.3∶8
C.3∶5 D.2∶5
A
A
B
C
D
E
——
——
6、判断题:
如图:DE∥BC, 下列各式是否正确
D:
——
——
=
AD
AE
AB
AC
( )
C:
——
——
=
AD
AC
AE
AB
( )
B:
——
——
=
AD
BD
AE
CE
( )
A:
AD
AB
=
AE
AC
( )
√
√
√
×
7.如图,已知l1∥l2∥l3,AM=3 cm,BM=5 cm,CM=4.5 cm,EF=12 cm,则DM=____cm,EK=____cm,FK=____cm.
7.5
4.5
7.5
F
BF=DE
DE
8.
DBFE
连续递推,豁然开朗
9.如图所示,在△ABC中,DE∥BC,EF∥DC.
求证:AD2=AB·AF.
证明:∵DE∥BC,∴AD∶AB=AE∶AC.
∵EF∥DC,∴AF∶AD=AE∶AC,
∴AD∶AB=AF∶AD,∴AD2=AB·AF.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
