4.3 相似三角形 课件(19张ppt)
文档属性
| 名称 | 4.3 相似三角形 课件(19张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-14 16:25:36 | ||
图片预览



文档简介
(共19张PPT)
浙教版九年级上册
4.3 相似三角形
第四章 相似三角形
温故知新
共同特征:
形状不变,大小改变
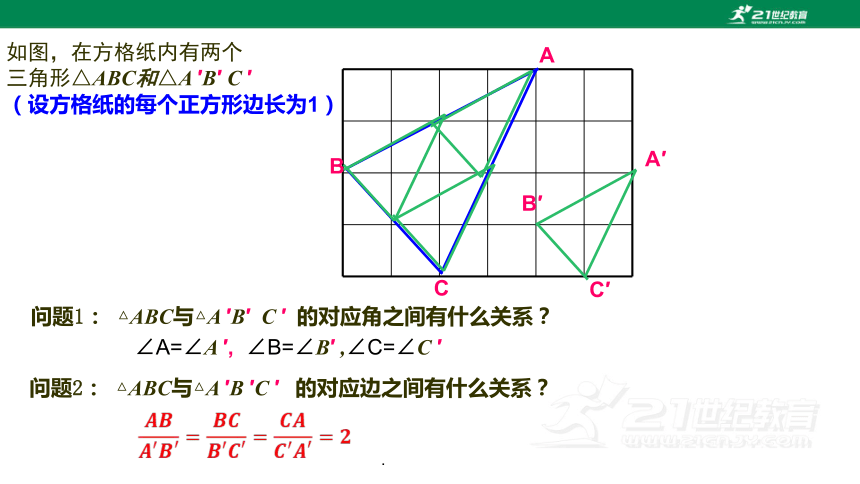
如图,在方格纸内有两个
三角形△ABC和△A ′B′ C ′
(设方格纸的每个正方形边长为1)
C
A
B
B′
A′
C′
问题2: △ABC与△A ′B ′C ′ 的对应边之间有什么关系?
问题1: △ABC与△A ′B′ C ′ 的对应角之间有什么关系?
∠A=∠A ′, ∠B=∠B′ ,∠C=∠C ′
.
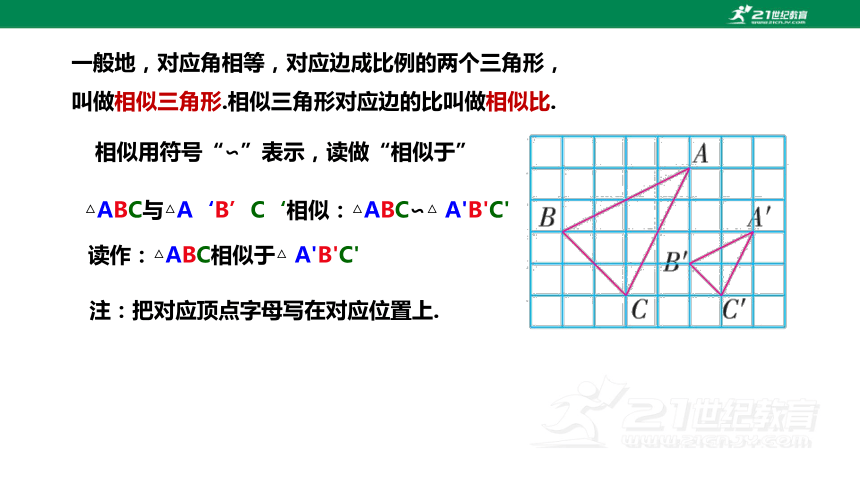
相似用符号“∽”表示,读做“相似于”
△ABC与△A‘B’C‘相似:△ABC∽△ A'B'C'
读作:△ABC相似于△ A'B'C'
注:把对应顶点字母写在对应位置上.
一般地,对应角相等,对应边成比例的两个三角形,
叫做相似三角形.相似三角形对应边的比叫做相似比.
相似三角形的性质:
相似三角形的对应角相等,对应边成比例.
几何语言:
对应角:
相似比:
,
.
.
,
.
对应点:点 与点 ;点
.
对应边: 与
.
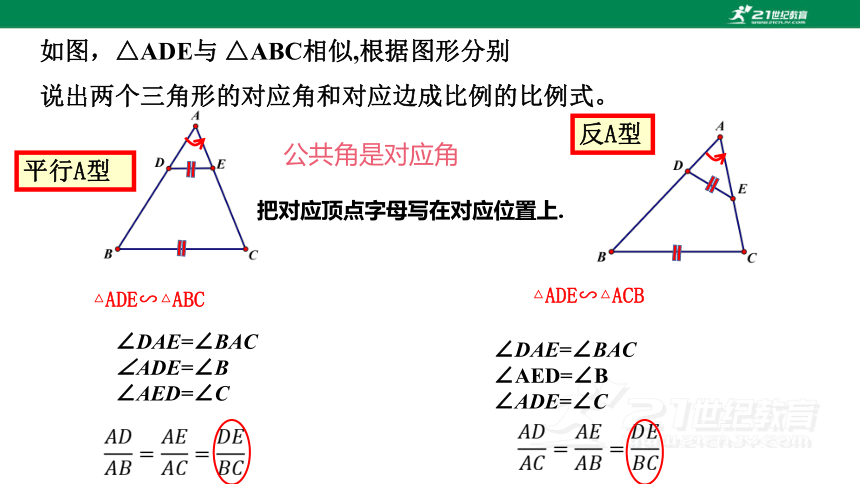
如图,△ADE与 △ABC相似,根据图形分别
说出两个三角形的对应角和对应边成比例的比例式。
∠DAE=∠BAC
∠ADE=∠B
∠AED=∠C
∠DAE=∠BAC
∠AED=∠B
∠ADE=∠C
公共角是对应角
△ADE∽△ABC
△ADE∽△ACB
把对应顶点字母写在对应位置上.
平行A型
反A型
.
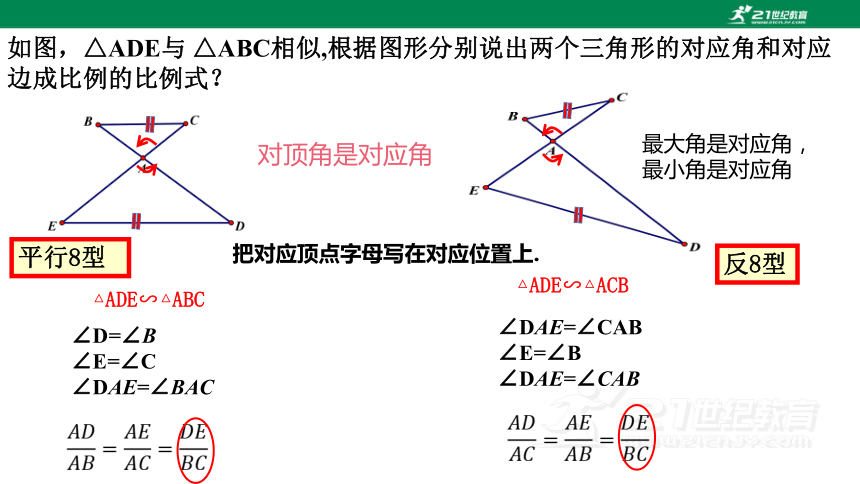
如图,△ADE与 △ABC相似,根据图形分别说出两个三角形的对应角和对应边成比例的比例式?
∠D=∠B
∠E=∠C
∠DAE=∠BAC
∠DAE=∠CAB
∠E=∠B
∠DAE=∠CAB
对顶角是对应角
最大角是对应角,
最小角是对应角
△ADE∽△ABC
△ADE∽△ACB
把对应顶点字母写在对应位置上.
平行8型
反8型
.
.
已知:如图,D,E分别是AB,AC边的中点.
求证:△ADE∽△ABC.
E
D
C
B
A
证明:
∵D,E分别是AB,AC的中点,
∴∠ADE=∠B,∠AED=∠C
在△ADE和△ABC中,
∠ADE=∠B,∠AED=∠C,∠A=∠A
=
=
=
∴DE∥BC,DE= BC.
∴△ADE∽△ABC
学以致用
已知: 如图, D、E分别是△ABC的AB, AC边上的点, △ABC∽△ADE.
已知 AD:DB=1:2, BC=9cm, 求DE的长.
E
D
C
B
A
解:∵△ABC ∽△ADE
∴DE=3(cm)
答:DE的长为3cm。
注意:AD:DB的比不是△ADE与△ABC的相似比。
.
.
.
即
.
确定相似三角形对应关系的两种方法
(2)结合图形确定.
归纳总结
(1)通过“”确定.
用“”连结的两个三角形对应顶点是确定的.
.
k≠1 两个形状相同,大小不等的相似三角形
k=1 两个全等三角形,是相似三角形的特例
(3) 相似比:
(对应边的比值)
30
45
夯实基础,稳扎稳打
1.判断对 “√ ” 错 “×”
(4)两个全等三角形一定相似。 ( )
(3)两个等边三角形一定相似。 ( )
(1)两个直角三角形一定相似。 ( )
(2)两个等腰三角形一定相似。 ( )
(5)两个等腰直角三角形一定相似. ( )
√
×
×
√
√
800
800
5.如图,D,E分别是AB,AC上两点,且AE=4,EC=2,AB=8,
若△AED∽△ABC,∠AED=∠B. 求AD的长.
解:∵△AED∽△ABC
∴
∵AE=4,EC=2,AB=8
∴
∴AD=3
相等的角是对应角
对应角所对的边是对应边
公共角是对应角
对应角所对的边是对应边
7.如图,D是AB上的一点。 △ABC∽ △ACD ,且AD:AC=2:3,
∠ADC= 65°, ∠B=37 °.
(1)求∠ACB, ∠ACD的度数;
(2)写出△ABC与 △ACD的对应边成比例的比例式,求出相似比。
A
D
C
B
(1)∠ACB=∠ADC= 65°,
∠ACD=∠B=37 °
(2)
.
.
.
8.如图,△ABC∽ △ACD,点D在AB上,
已知AC=3cm,AD=2cm,求AB的长
△ABC∽ △ACD
.
32=2×AB
AC
AD、AB比例中项
△ABC与△ACD的公共边
AC2=AD AB
AB=
.
连续递推,豁然开朗
对应点、对应边、对应角已确定
9.
浙教版九年级上册
4.3 相似三角形
第四章 相似三角形
温故知新
共同特征:
形状不变,大小改变
如图,在方格纸内有两个
三角形△ABC和△A ′B′ C ′
(设方格纸的每个正方形边长为1)
C
A
B
B′
A′
C′
问题2: △ABC与△A ′B ′C ′ 的对应边之间有什么关系?
问题1: △ABC与△A ′B′ C ′ 的对应角之间有什么关系?
∠A=∠A ′, ∠B=∠B′ ,∠C=∠C ′
.
相似用符号“∽”表示,读做“相似于”
△ABC与△A‘B’C‘相似:△ABC∽△ A'B'C'
读作:△ABC相似于△ A'B'C'
注:把对应顶点字母写在对应位置上.
一般地,对应角相等,对应边成比例的两个三角形,
叫做相似三角形.相似三角形对应边的比叫做相似比.
相似三角形的性质:
相似三角形的对应角相等,对应边成比例.
几何语言:
对应角:
相似比:
,
.
.
.
.
.
如图,△ADE与 △ABC相似,根据图形分别
说出两个三角形的对应角和对应边成比例的比例式。
∠DAE=∠BAC
∠ADE=∠B
∠AED=∠C
∠DAE=∠BAC
∠AED=∠B
∠ADE=∠C
公共角是对应角
△ADE∽△ABC
△ADE∽△ACB
把对应顶点字母写在对应位置上.
平行A型
反A型
.
如图,△ADE与 △ABC相似,根据图形分别说出两个三角形的对应角和对应边成比例的比例式?
∠D=∠B
∠E=∠C
∠DAE=∠BAC
∠DAE=∠CAB
∠E=∠B
∠DAE=∠CAB
对顶角是对应角
最大角是对应角,
最小角是对应角
△ADE∽△ABC
△ADE∽△ACB
把对应顶点字母写在对应位置上.
平行8型
反8型
.
.
已知:如图,D,E分别是AB,AC边的中点.
求证:△ADE∽△ABC.
E
D
C
B
A
证明:
∵D,E分别是AB,AC的中点,
∴∠ADE=∠B,∠AED=∠C
在△ADE和△ABC中,
∠ADE=∠B,∠AED=∠C,∠A=∠A
=
=
=
∴DE∥BC,DE= BC.
∴△ADE∽△ABC
学以致用
已知: 如图, D、E分别是△ABC的AB, AC边上的点, △ABC∽△ADE.
已知 AD:DB=1:2, BC=9cm, 求DE的长.
E
D
C
B
A
解:∵△ABC ∽△ADE
∴DE=3(cm)
答:DE的长为3cm。
注意:AD:DB的比不是△ADE与△ABC的相似比。
.
.
.
即
.
确定相似三角形对应关系的两种方法
(2)结合图形确定.
归纳总结
(1)通过“”确定.
用“”连结的两个三角形对应顶点是确定的.
.
k≠1 两个形状相同,大小不等的相似三角形
k=1 两个全等三角形,是相似三角形的特例
(3) 相似比:
(对应边的比值)
30
45
夯实基础,稳扎稳打
1.判断对 “√ ” 错 “×”
(4)两个全等三角形一定相似。 ( )
(3)两个等边三角形一定相似。 ( )
(1)两个直角三角形一定相似。 ( )
(2)两个等腰三角形一定相似。 ( )
(5)两个等腰直角三角形一定相似. ( )
√
×
×
√
√
800
800
5.如图,D,E分别是AB,AC上两点,且AE=4,EC=2,AB=8,
若△AED∽△ABC,∠AED=∠B. 求AD的长.
解:∵△AED∽△ABC
∴
∵AE=4,EC=2,AB=8
∴
∴AD=3
相等的角是对应角
对应角所对的边是对应边
公共角是对应角
对应角所对的边是对应边
7.如图,D是AB上的一点。 △ABC∽ △ACD ,且AD:AC=2:3,
∠ADC= 65°, ∠B=37 °.
(1)求∠ACB, ∠ACD的度数;
(2)写出△ABC与 △ACD的对应边成比例的比例式,求出相似比。
A
D
C
B
(1)∠ACB=∠ADC= 65°,
∠ACD=∠B=37 °
(2)
.
.
.
8.如图,△ABC∽ △ACD,点D在AB上,
已知AC=3cm,AD=2cm,求AB的长
△ABC∽ △ACD
.
32=2×AB
AC
AD、AB比例中项
△ABC与△ACD的公共边
AC2=AD AB
AB=
.
连续递推,豁然开朗
对应点、对应边、对应角已确定
9.
同课章节目录
