探索勾股定理(第一课时)(浙江省宁波市)
文档属性
| 名称 | 探索勾股定理(第一课时)(浙江省宁波市) |  | |
| 格式 | rar | ||
| 文件大小 | 965.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-12-16 22:03:00 | ||
图片预览





文档简介
课件23张PPT。探索勾股定理(1) 执教者:余姚市历山中学 景祝君主体育场——“鸟巢”
第一展厅:“鸟巢”是2008年北京奥运会主体育场。由2001年普利茨克奖获得者赫尔佐格、德梅隆与中国建筑师合作完成的巨型体育场设计,形态如同孕育生命的“巢”,它更像一个摇篮, 寄托着人类对未来的希望。设计者们对这个国家体育场没有做任何多余的处理,只是坦率地把结构暴露在外,因而自然形成了建筑的外观。 主体育场——“鸟巢”
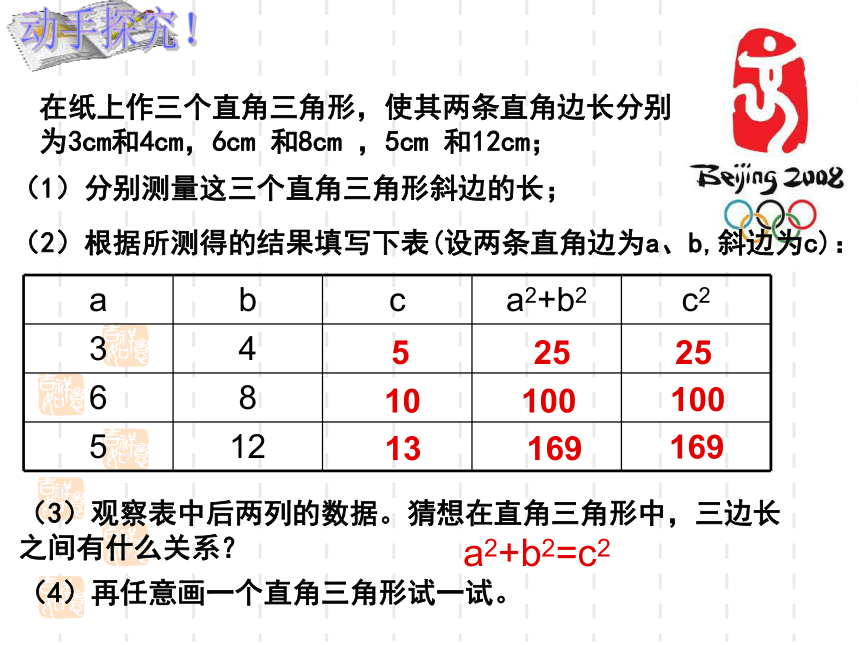
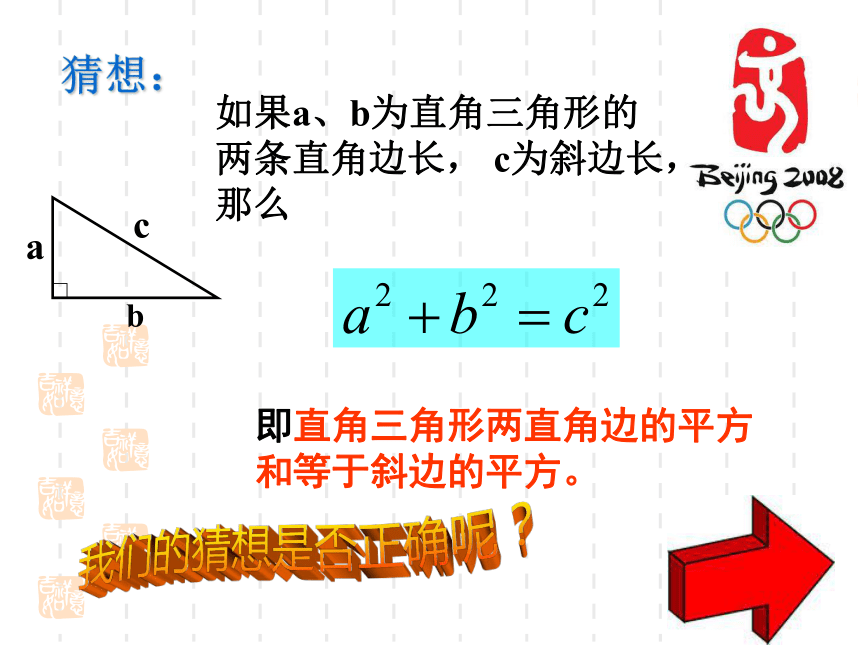
第一展厅:“鸟巢”外部围绕一片美丽的莲花池。在平静的湖面上,有一支红莲,高出水面1米,红莲被风一吹,花朵刚好与水面平齐。已知红莲移动的水平距离是5米,问这里的水深是多少呢?智慧书!动手探究!在纸上作三个直角三角形,使其两条直角边长分别为3cm和4cm,6cm 和8cm ,5cm 和12cm;(1)分别测量这三个直角三角形斜边的长;(2)根据所测得的结果填写下表(设两条直角边为a、b,斜边为c):(3)观察表中后两列的数据。猜想在直角三角形中,三边长之间有什么关系?510132510016925169100(4)再任意画一个直角三角形试一试。a2+b2=c2猜想:如果a、b为直角三角形的两条直角边长, c为斜边长,那么即直角三角形两直角边的平方和等于斜边的平方。我们的猜想是否正确呢?国家游泳中心——“水立方”
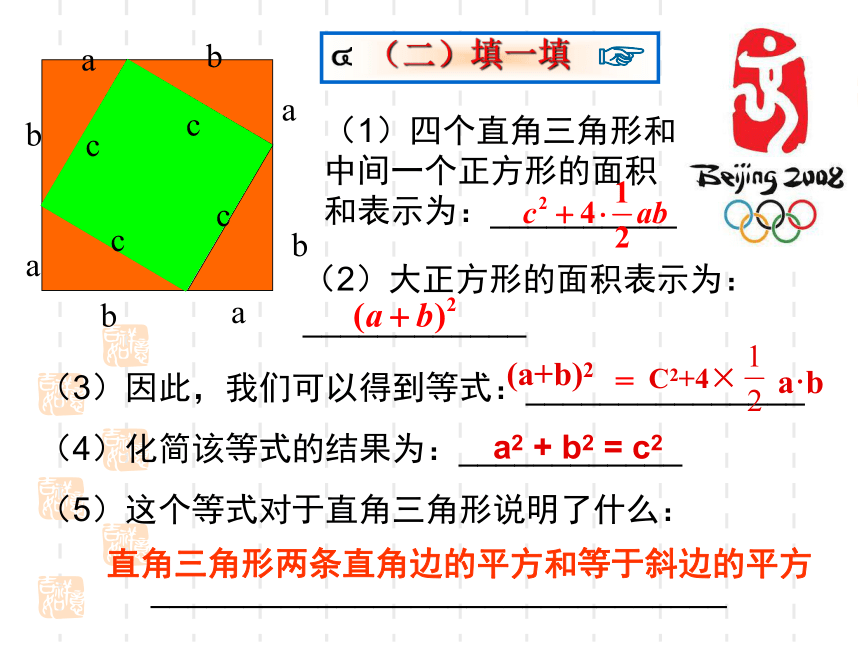
第二展厅:“鸟巢”旁边的是国家游泳中心,因外形酷似一个充满了水泡的蓝色方盒子而被称为“水立方”,由中国和澳大利 亚的联合设计团队设计。 “水立方”里面的顶部以及四周围仿佛是一个一个水分子拼接而成,纷繁自由的结构形式,简洁纯净的体形谦虚地与宏伟的主场对话,不同气质的对比使各自的灵性得到趣味盎然的共生。(1)四个直角三角形和中间一个正方形的面积和表示为:__________(2)大正方形的面积表示为:____________(3)因此,我们可以得到等式:_______________(4)化简该等式的结果为:____________(5)这个等式对于直角三角形说明了什么:
_______________________________a2 + b2 = c2直角三角形两条直角边的平方和等于斜边的平方┏a2+b2=c2acb 直角三角形两条直角边的平方和等于斜边的平方.勾股弦 勾股定理(毕达哥拉斯定理) 两千多年前,古希腊有个哥拉 斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯年希腊曾经发行了一枚纪念票。定理。为了纪念毕达哥拉斯学派,1955勾 股 世 界国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前 两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。 我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。看看谁算得快!82+x2=172x2+162=20252+122=x2∴x2=172-82
=225又∵x>0
∴x=15∴x2=202-162
=144又∵x>0
∴x=12∴x2=52+122
=169又∵x>0
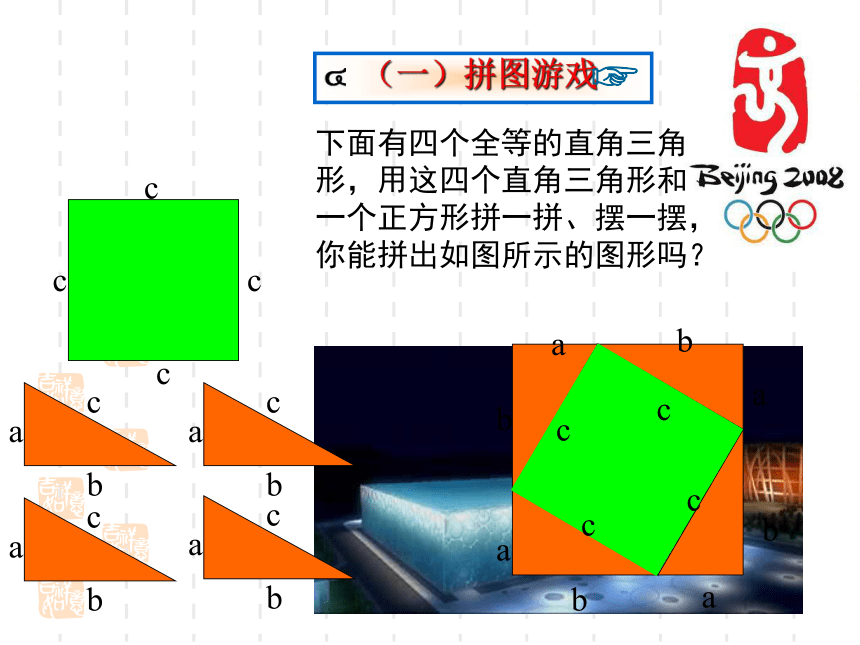
∴x=13可用勾股定理建立方程.方法小结:由勾股定理得:由勾股定理得:由勾股定理得:即a2+b2=c2利用刚才的四块直角三角形和一个白色的正方形,你能拼出一个外围边长为c的正方形吗?欢迎各位同学来到奥运会比赛场地参观,我们是奥运会的吉祥物:贝贝、晶晶、欢欢、迎迎、妮妮,我们有些问题想考同学们,过了我们这一关,才能进入第三展厅已知在△ABC中,∠C=Rt∠,BC=a,AC=b,AB=c.
(1)若a=1,b=2,求c;(2)a=15,c=17,求b;(3)c=34,a:b=8:15,求a,b.已知直角三角形两边的长分别为3cm,4cm,求第三边的边长。 直角三角形中两条直角边之比为3:4,且斜边为10cm。求:
(1)两直角边的长;
(2)斜边上的高线长。已知△ABC中,∠A =Rt∠,BC=a,AC=b,AB=c。若b=8,c=15,求a。 你能利用直角三角形在数轴上表示点 吗?欢迎您来到第三展厅第三展厅:
国家体育馆——“中国折扇”下图是一个
长方形的结构图,
根据所给的尺寸
(单位:m),
求机器人从A地走到B地最少需要走的距离。波浪式造型的屋面轻盈而富于动感,虽然赋予了国家体育馆灵动之美,但也为施工带来了困难。为了给国家体育馆屋顶架上钢屋架,施工技术人员首次采用了9个“机器人”进行的滑移施工技术,可以让机器人好比蜗牛背着大贝壳行走一样,背着几百吨钢屋架行走到设定位置。 下图是一个长方形的结构图,根据所给的尺寸(单位:m),求机器人从A地走到B地最少需要走的距离。C解:过A作铅垂线,过B作水平线,两线交于点C,则
∠ACB=90°,
AC=90-40=50(mm)
BC=160-40=120(mm)由勾股定理,得
AB2=AC2+BC2=502+1202=16900(mm2)∵AB>0∴AB=130mm答:两孔中心A,B之间的距离为130mm“鸟巢”外部围绕一片美丽的莲花池。在平静的湖面上,有一支红莲,高出水面1米,红莲被风一吹,花朵刚好与水面平齐。已知红莲移动的水平距离是5米,问这里的水深是多少呢?解:设水深x米,则红莲长(x+1)米,则 x2+52=(x+1)2解得 x=12(米)答:这里的水深是12米问题三:在这堂课里,你最大的收获是什么?
最愉悦的事情是什么?你说我说大家说问题一:这堂课我们主要学了哪些知识?问题二:这堂课我们体会到了哪些数学思维方法?必做题:作业题A组
选做题:1、作业题C组
2、上网查找有关利用拼图来验证勾股定理证明的方法,每人至少能说出一种与课本不一样的方法,若有好的方法可用小论文的形式写出来。作业布置谢谢!
第一展厅:“鸟巢”是2008年北京奥运会主体育场。由2001年普利茨克奖获得者赫尔佐格、德梅隆与中国建筑师合作完成的巨型体育场设计,形态如同孕育生命的“巢”,它更像一个摇篮, 寄托着人类对未来的希望。设计者们对这个国家体育场没有做任何多余的处理,只是坦率地把结构暴露在外,因而自然形成了建筑的外观。 主体育场——“鸟巢”
第一展厅:“鸟巢”外部围绕一片美丽的莲花池。在平静的湖面上,有一支红莲,高出水面1米,红莲被风一吹,花朵刚好与水面平齐。已知红莲移动的水平距离是5米,问这里的水深是多少呢?智慧书!动手探究!在纸上作三个直角三角形,使其两条直角边长分别为3cm和4cm,6cm 和8cm ,5cm 和12cm;(1)分别测量这三个直角三角形斜边的长;(2)根据所测得的结果填写下表(设两条直角边为a、b,斜边为c):(3)观察表中后两列的数据。猜想在直角三角形中,三边长之间有什么关系?510132510016925169100(4)再任意画一个直角三角形试一试。a2+b2=c2猜想:如果a、b为直角三角形的两条直角边长, c为斜边长,那么即直角三角形两直角边的平方和等于斜边的平方。我们的猜想是否正确呢?国家游泳中心——“水立方”
第二展厅:“鸟巢”旁边的是国家游泳中心,因外形酷似一个充满了水泡的蓝色方盒子而被称为“水立方”,由中国和澳大利 亚的联合设计团队设计。 “水立方”里面的顶部以及四周围仿佛是一个一个水分子拼接而成,纷繁自由的结构形式,简洁纯净的体形谦虚地与宏伟的主场对话,不同气质的对比使各自的灵性得到趣味盎然的共生。(1)四个直角三角形和中间一个正方形的面积和表示为:__________(2)大正方形的面积表示为:____________(3)因此,我们可以得到等式:_______________(4)化简该等式的结果为:____________(5)这个等式对于直角三角形说明了什么:
_______________________________a2 + b2 = c2直角三角形两条直角边的平方和等于斜边的平方┏a2+b2=c2acb 直角三角形两条直角边的平方和等于斜边的平方.勾股弦 勾股定理(毕达哥拉斯定理) 两千多年前,古希腊有个哥拉 斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯年希腊曾经发行了一枚纪念票。定理。为了纪念毕达哥拉斯学派,1955勾 股 世 界国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前 两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。 我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。看看谁算得快!82+x2=172x2+162=20252+122=x2∴x2=172-82
=225又∵x>0
∴x=15∴x2=202-162
=144又∵x>0
∴x=12∴x2=52+122
=169又∵x>0
∴x=13可用勾股定理建立方程.方法小结:由勾股定理得:由勾股定理得:由勾股定理得:即a2+b2=c2利用刚才的四块直角三角形和一个白色的正方形,你能拼出一个外围边长为c的正方形吗?欢迎各位同学来到奥运会比赛场地参观,我们是奥运会的吉祥物:贝贝、晶晶、欢欢、迎迎、妮妮,我们有些问题想考同学们,过了我们这一关,才能进入第三展厅已知在△ABC中,∠C=Rt∠,BC=a,AC=b,AB=c.
(1)若a=1,b=2,求c;(2)a=15,c=17,求b;(3)c=34,a:b=8:15,求a,b.已知直角三角形两边的长分别为3cm,4cm,求第三边的边长。 直角三角形中两条直角边之比为3:4,且斜边为10cm。求:
(1)两直角边的长;
(2)斜边上的高线长。已知△ABC中,∠A =Rt∠,BC=a,AC=b,AB=c。若b=8,c=15,求a。 你能利用直角三角形在数轴上表示点 吗?欢迎您来到第三展厅第三展厅:
国家体育馆——“中国折扇”下图是一个
长方形的结构图,
根据所给的尺寸
(单位:m),
求机器人从A地走到B地最少需要走的距离。波浪式造型的屋面轻盈而富于动感,虽然赋予了国家体育馆灵动之美,但也为施工带来了困难。为了给国家体育馆屋顶架上钢屋架,施工技术人员首次采用了9个“机器人”进行的滑移施工技术,可以让机器人好比蜗牛背着大贝壳行走一样,背着几百吨钢屋架行走到设定位置。 下图是一个长方形的结构图,根据所给的尺寸(单位:m),求机器人从A地走到B地最少需要走的距离。C解:过A作铅垂线,过B作水平线,两线交于点C,则
∠ACB=90°,
AC=90-40=50(mm)
BC=160-40=120(mm)由勾股定理,得
AB2=AC2+BC2=502+1202=16900(mm2)∵AB>0∴AB=130mm答:两孔中心A,B之间的距离为130mm“鸟巢”外部围绕一片美丽的莲花池。在平静的湖面上,有一支红莲,高出水面1米,红莲被风一吹,花朵刚好与水面平齐。已知红莲移动的水平距离是5米,问这里的水深是多少呢?解:设水深x米,则红莲长(x+1)米,则 x2+52=(x+1)2解得 x=12(米)答:这里的水深是12米问题三:在这堂课里,你最大的收获是什么?
最愉悦的事情是什么?你说我说大家说问题一:这堂课我们主要学了哪些知识?问题二:这堂课我们体会到了哪些数学思维方法?必做题:作业题A组
选做题:1、作业题C组
2、上网查找有关利用拼图来验证勾股定理证明的方法,每人至少能说出一种与课本不一样的方法,若有好的方法可用小论文的形式写出来。作业布置谢谢!
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
