与面积有关的二次函数复习(浙江省宁波市)
文档属性
| 名称 | 与面积有关的二次函数复习(浙江省宁波市) |

|
|
| 格式 | rar | ||
| 文件大小 | 324.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-05-13 00:00:00 | ||
图片预览



文档简介
课件9张PPT。与面积有关的
二次函数综合复习 田莘耕中学 初三
林培娟1、什么叫做二次函数?它的图象是什么?它的对称轴、顶点坐标各是什么?
答:y=ax2+bx+c(a,b,c是常数,a≠0),y叫做x的二次函数。它的图象是一条抛物线。它的对称轴是直线x= ,顶点坐标是( , )。
2、二次函数的解析式有哪几种? ⑶交点式:y = a(x-x1)(x-x2) 与x轴两交点:(x1,0),(x2,0) 对称轴为(x1+x2) /2
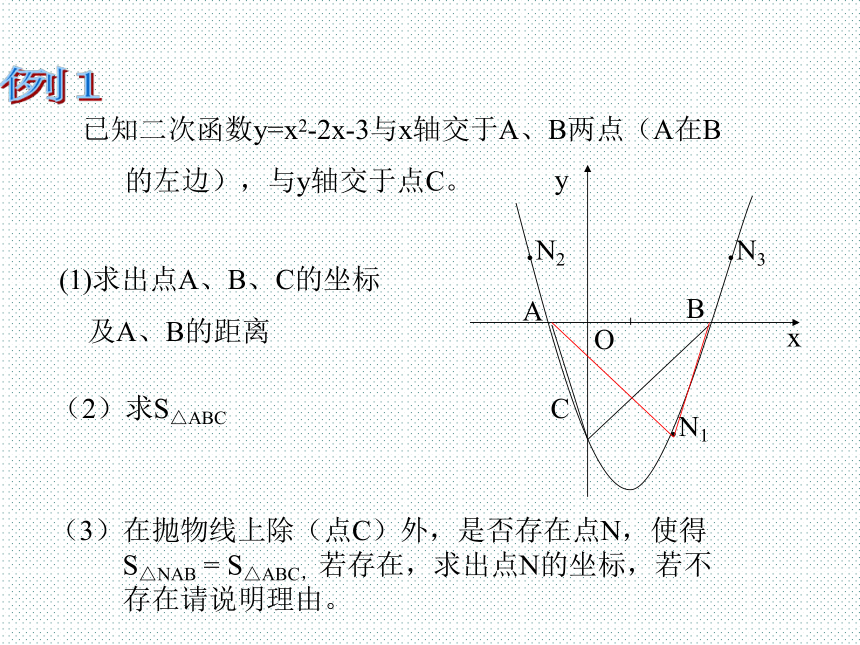
有三种:⑴一般式:y = ax2+bx+c(a≠0)⑵顶点式:y = a(x-h)2+k 顶点 为(h,k) 已知二次函数y=x2-2x-3与x轴交于A、B两点(A在B
的左边),与y轴交于点C。(1)求出点A、B、C的坐标
及A、B的距离(2)求S△ABC(3)在抛物线上除(点C)外,是否存在点N,使得
S△NAB = S△ABC,若存在,求出点N的坐标,若不
存在请说明理由。.N1例1.N2.N3注意:由条件探索结论”存在性”的探索性问题的解题思路:假设”存在”—演绎推理—得出结论(合理或矛盾) 如图所示,已知抛物线y=ax2+bx+c(a≠0)与x轴相交
于两点A(x1,0) B(x2,0)(x1 半轴相交于点C,若抛物线顶点P的横坐标是1,A、
B两点间的距离为4,且△ABC的面积为6。(1)求点A和B的坐标(2)求此抛物线的解析式(3)求四边形ACPB的面积
例2HH 如图所示,已知抛物线y=ax2+bx+c(a≠0)与x轴相交
于两点A(x1,0) B(x2,0)(x1 半轴相交于点C,若抛物线顶点P的横坐标是1,A、
B两点间的距离为4,且△ABC的面积为6。(1)求点A和B的坐标(2)求此抛物线的解析式(3)求四边形ACPB的面积(4)设M(x,y)(其中0 抛物线上的一个动点,试求四边
形OCMB的最大值,及此时点M的坐标。.M例2 由条件探索结论”存在性”的探索性问题的解题思路:假设”存在”—演绎推理—得出结论(合理或矛盾)非规则四边形的面积用割补法转化为若干个三角形或四边形的面积,且其中一边与坐标轴平行或重合,使问题得到解决。小结谢谢
二次函数综合复习 田莘耕中学 初三
林培娟1、什么叫做二次函数?它的图象是什么?它的对称轴、顶点坐标各是什么?
答:y=ax2+bx+c(a,b,c是常数,a≠0),y叫做x的二次函数。它的图象是一条抛物线。它的对称轴是直线x= ,顶点坐标是( , )。
2、二次函数的解析式有哪几种? ⑶交点式:y = a(x-x1)(x-x2) 与x轴两交点:(x1,0),(x2,0) 对称轴为(x1+x2) /2
有三种:⑴一般式:y = ax2+bx+c(a≠0)⑵顶点式:y = a(x-h)2+k 顶点 为(h,k) 已知二次函数y=x2-2x-3与x轴交于A、B两点(A在B
的左边),与y轴交于点C。(1)求出点A、B、C的坐标
及A、B的距离(2)求S△ABC(3)在抛物线上除(点C)外,是否存在点N,使得
S△NAB = S△ABC,若存在,求出点N的坐标,若不
存在请说明理由。.N1例1.N2.N3注意:由条件探索结论”存在性”的探索性问题的解题思路:假设”存在”—演绎推理—得出结论(合理或矛盾) 如图所示,已知抛物线y=ax2+bx+c(a≠0)与x轴相交
于两点A(x1,0) B(x2,0)(x1
B两点间的距离为4,且△ABC的面积为6。(1)求点A和B的坐标(2)求此抛物线的解析式(3)求四边形ACPB的面积
例2HH 如图所示,已知抛物线y=ax2+bx+c(a≠0)与x轴相交
于两点A(x1,0) B(x2,0)(x1
B两点间的距离为4,且△ABC的面积为6。(1)求点A和B的坐标(2)求此抛物线的解析式(3)求四边形ACPB的面积(4)设M(x,y)(其中0
形OCMB的最大值,及此时点M的坐标。.M例2 由条件探索结论”存在性”的探索性问题的解题思路:假设”存在”—演绎推理—得出结论(合理或矛盾)非规则四边形的面积用割补法转化为若干个三角形或四边形的面积,且其中一边与坐标轴平行或重合,使问题得到解决。小结谢谢
同课章节目录
