1.5.4三角形全等的判定 AAS 课件(共20张PPT) 2023—2024学年浙教版数学八年级上册
文档属性
| 名称 | 1.5.4三角形全等的判定 AAS 课件(共20张PPT) 2023—2024学年浙教版数学八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 548.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-17 15:47:18 | ||
图片预览

文档简介
(共20张PPT)
④
三边对应相等的两个三角形全等(SSS)
.
1
两边及其夹角对应相等的两个三角形全等(SAS)
2
判定方法
两个角及其夹边对应相等的两个三角形全等(ASA)
3
我们学过哪几种判定三角形全等的方法
归纳
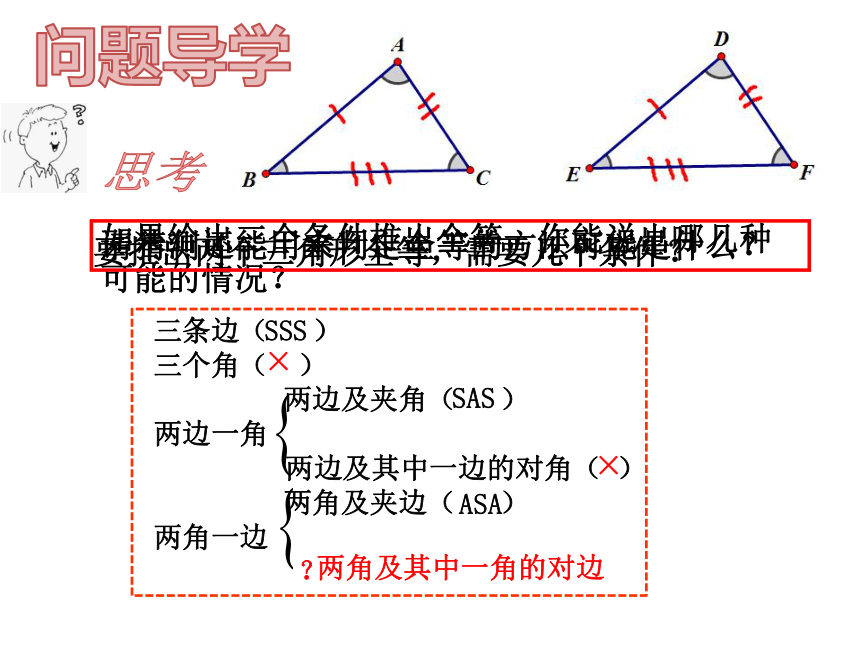
要推出两个三角形全等,需要几个条件?
如果给出三个条件推出全等,你能说出哪几种可能的情况?
思考
三条边( )
三个角( )
两边及夹角( )
两边一角
两边及其中一边的对角( )
两角及夹边( )
两角一边
?
请猜测还能用来判定全等的方法可能是什么?
问题导学
SSS
×
SAS
×
ASA
两角及其中一角的对边
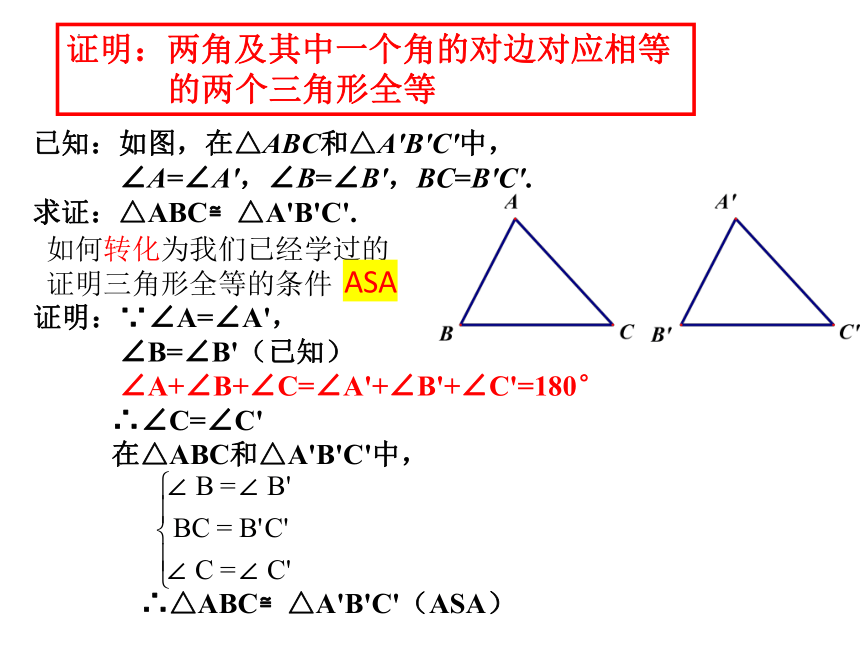
已知:如图,在△ABC和△A'B'C'中,
∠A=∠A',∠B=∠B',BC=B'C'.
求证:△ABC≌△A'B'C'.
证明:∵∠A=∠A',
∠B=∠B'(已知)
∠A+∠B+∠C=∠A'+∠B'+∠C'=180°
∴∠C=∠C'
在△ABC和△A'B'C'中,
∴△ABC≌△A'B'C'(ASA)
证明:两角及其中一个角的对边对应相等
的两个三角形全等
如何转化为我们已经学过的证明三角形全等的条件
ASA
问题呈现
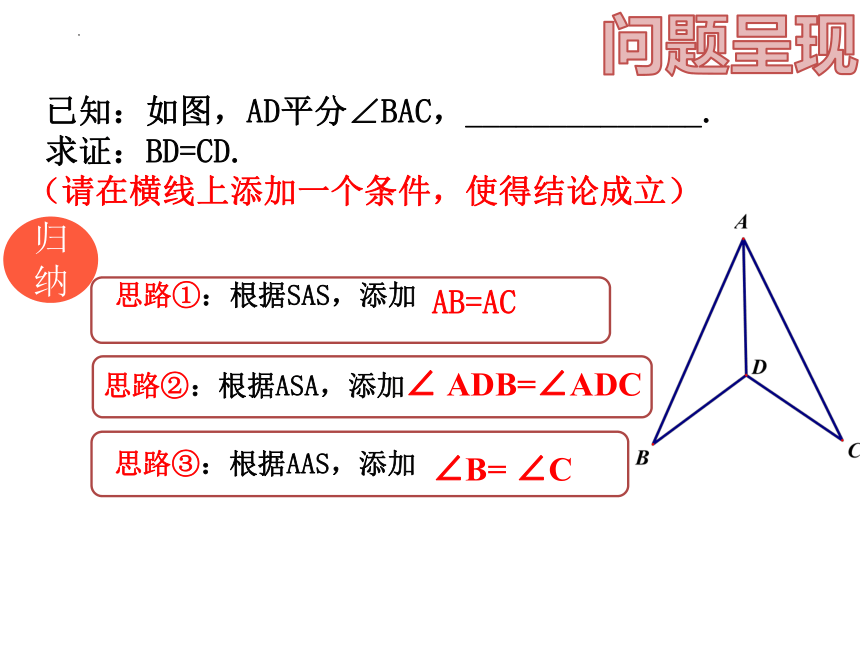
已知:如图,AD平分∠BAC,______________.
求证:BD=CD.
(请在横线上添加一个条件,使得结论成立)
归纳
思路①:根据SAS,添加
思路②:根据ASA,添加
思路③:根据AAS,添加
AB=AC
∠ ADB=∠ADC
∠B= ∠C
问题呈现
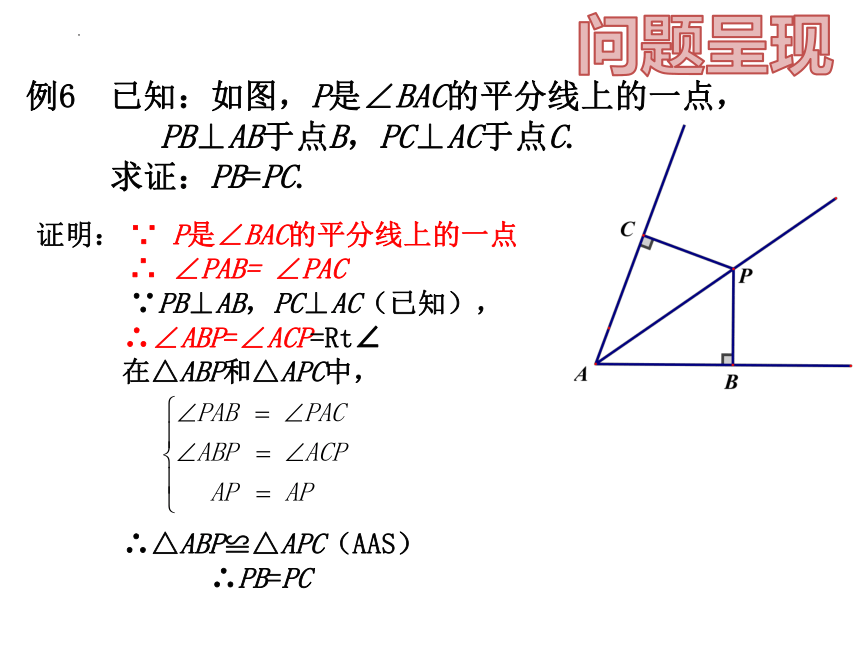
例6 已知:如图,P是∠BAC的平分线上的一点,
PB⊥AB于点B,PC⊥AC于点C.
求证:PB=PC.
证明: ∵ P是∠BAC的平分线上的一点
∴ ∠PAB= ∠PAC
∵PB⊥AB,PC⊥AC(已知),
∴∠ABP=∠ACP=Rt∠
在△ABP和△APC中,
∴△ABP≌△APC(AAS)
∴PB=PC
问题导学
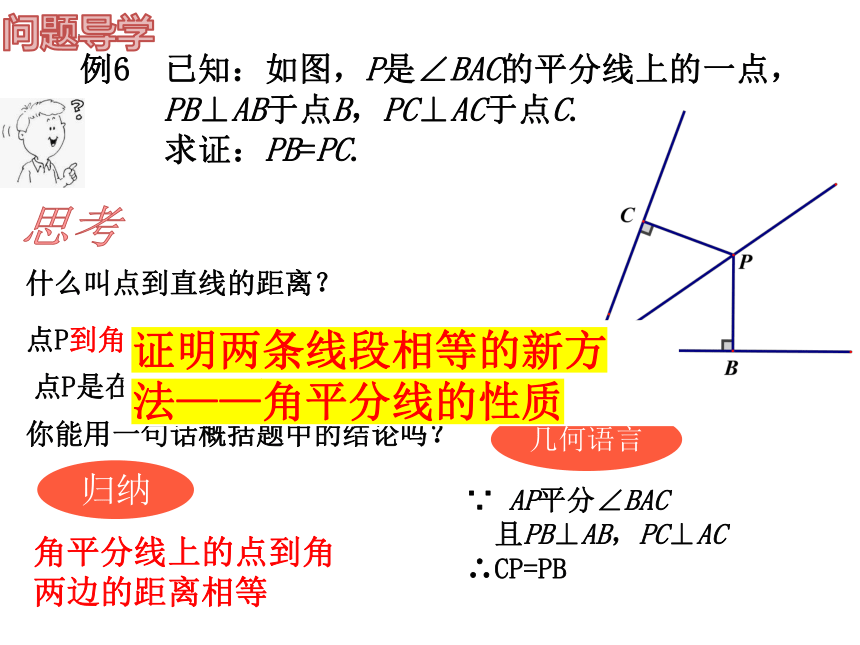
例6 已知:如图,P是∠BAC的平分线上的一点,
PB⊥AB于点B,PC⊥AC于点C.
求证:PB=PC.
思考
什么叫点到直线的距离?
归纳
角平分线上的点到角两边的距离相等
点P到角两边的距离指哪两条垂线段的长?
你能用一句话概括题中的结论吗?
点P是在哪里的点
∵ AP平分∠BAC
且PB⊥AB,PC⊥AC
∴CP=PB
几何语言
证明两条线段相等的新方法——角平分线的性质
问题呈现
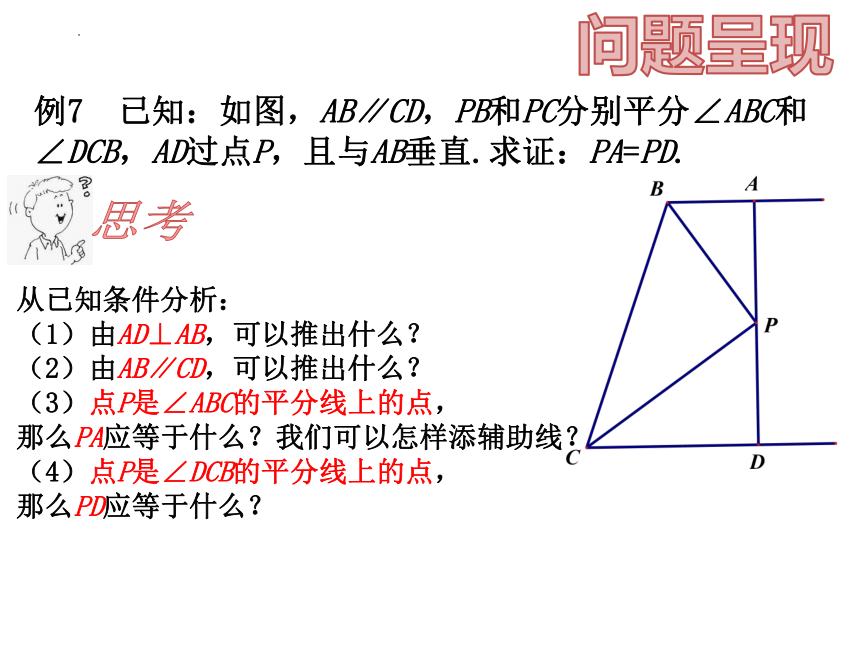
例7 已知:如图,AB∥CD,PB和PC分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.求证:PA=PD.
思考
从已知条件分析:
(1)由AD⊥AB,可以推出什么?
(2)由AB∥CD,可以推出什么?
(3)点P是∠ABC的平分线上的点,
那么PA应等于什么?我们可以怎样添辅助线?
(4)点P是∠DCB的平分线上的点,
那么PD应等于什么?
问题导学
例7 已知:如图,AB∥CD,PB和PC分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.求证:PA=PD.
分析
AB∥CD
AD过点P,且与AB垂直
∠BAD+∠CDA= 180°
∠BAD= 90°
∠CDA= 90°
BP平分∠ABC
CP平分∠DCB
PA ⊥ BA
PD⊥ CD
PA =
PD=
归纳
几何证明的方法:综合法
过点P作PE⊥BC于点E
问题导学
为了证明PA=PD,不是直接证明这两条线段相等,而是分别证明它们与哪条线段相等?这种思考方法对你有怎样的启发?
思考
归纳
当图形中没有现成的全等三角形时,
必须通过添加适当的辅助线,构造出所
需要的全等三角形
(p36.3)证明:三角形的两条角平分线的交点到各边的距离相等
已知:如图, △ABC的角平分线BD,CE相交于点P。
求证:点P到三边的距离相等。
证明:过点P做PL⊥AB交AB于点L,过点P做PM⊥BC交BC于点M,过点P做PN⊥AC交AC于点N
∵BP平分∠ABC,且PL⊥AB, PM⊥BC
∴PL=PM
同理可证 PN=PM
即PL=PM=PN
已知:如图, △ABC的角平分线BD,CE相交于点P。
且AB=7,BC=8,AC=9,PM=3,求△ABC的面积
全校A P13 题10
作业本1 P11 题6
问题呈现
思考
已知:如图,AD垂直平分BC,D为垂足.
DM⊥AC,DN⊥AB,M,N分别为垂足.
求证:DM=DN.
从已知条件分析:
(1)AD垂直平分BC,你能得到哪些结论?
(2)DM⊥AC,DN⊥AB,你又能得到哪些结论?
从结论出发分析:
要证明DM=DN,你会想到哪些方法?
思路①:通过证两次三角形全等来得到.
AD垂直平分BC
∠ADC=∠ADB=90°
BD=CD
AD=AD
△ADC≌△ADB
∠CAD=∠BAD
∠C=∠B
△ADM≌△ADN
△MDC≌△NDB
DM=DN
DM=DN
一题多解
(SAS)
(AAS)
(AAS)
思路②:通过证一次全等,再利用
角平分线性质来得到.
△ADC≌△ADB
∠CAD=∠BAD
DM⊥AC,DN⊥AB
DM=DN
一题多解
思路③:利用面积法来得到.
AD垂直平分BC
AB=AC
S△ADC=S△ADB
DM=DN
AB=AC
一题多解
AD是ABC的中线
证明两条线段相等的新方法
——面积法(利用面积相等)
1
当题中出现全等三角形的时候,可以利用全等三角形对应边相等
2
当题中出现角平分线的时候,可以利用角平分线的性质定理
3
当题中具有面积相等的三角形时,可以试试面积法
证明两条线段相等的方法有哪些?
归纳
碰到几何证明题,我们可以如何进行分析呢?
归纳
从已知条件和结论两个角度入手进行分析.
盘点收获
布置作业
④
三边对应相等的两个三角形全等(SSS)
.
1
两边及其夹角对应相等的两个三角形全等(SAS)
2
判定方法
两个角及其夹边对应相等的两个三角形全等(ASA)
3
我们学过哪几种判定三角形全等的方法
归纳
要推出两个三角形全等,需要几个条件?
如果给出三个条件推出全等,你能说出哪几种可能的情况?
思考
三条边( )
三个角( )
两边及夹角( )
两边一角
两边及其中一边的对角( )
两角及夹边( )
两角一边
?
请猜测还能用来判定全等的方法可能是什么?
问题导学
SSS
×
SAS
×
ASA
两角及其中一角的对边
已知:如图,在△ABC和△A'B'C'中,
∠A=∠A',∠B=∠B',BC=B'C'.
求证:△ABC≌△A'B'C'.
证明:∵∠A=∠A',
∠B=∠B'(已知)
∠A+∠B+∠C=∠A'+∠B'+∠C'=180°
∴∠C=∠C'
在△ABC和△A'B'C'中,
∴△ABC≌△A'B'C'(ASA)
证明:两角及其中一个角的对边对应相等
的两个三角形全等
如何转化为我们已经学过的证明三角形全等的条件
ASA
问题呈现
已知:如图,AD平分∠BAC,______________.
求证:BD=CD.
(请在横线上添加一个条件,使得结论成立)
归纳
思路①:根据SAS,添加
思路②:根据ASA,添加
思路③:根据AAS,添加
AB=AC
∠ ADB=∠ADC
∠B= ∠C
问题呈现
例6 已知:如图,P是∠BAC的平分线上的一点,
PB⊥AB于点B,PC⊥AC于点C.
求证:PB=PC.
证明: ∵ P是∠BAC的平分线上的一点
∴ ∠PAB= ∠PAC
∵PB⊥AB,PC⊥AC(已知),
∴∠ABP=∠ACP=Rt∠
在△ABP和△APC中,
∴△ABP≌△APC(AAS)
∴PB=PC
问题导学
例6 已知:如图,P是∠BAC的平分线上的一点,
PB⊥AB于点B,PC⊥AC于点C.
求证:PB=PC.
思考
什么叫点到直线的距离?
归纳
角平分线上的点到角两边的距离相等
点P到角两边的距离指哪两条垂线段的长?
你能用一句话概括题中的结论吗?
点P是在哪里的点
∵ AP平分∠BAC
且PB⊥AB,PC⊥AC
∴CP=PB
几何语言
证明两条线段相等的新方法——角平分线的性质
问题呈现
例7 已知:如图,AB∥CD,PB和PC分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.求证:PA=PD.
思考
从已知条件分析:
(1)由AD⊥AB,可以推出什么?
(2)由AB∥CD,可以推出什么?
(3)点P是∠ABC的平分线上的点,
那么PA应等于什么?我们可以怎样添辅助线?
(4)点P是∠DCB的平分线上的点,
那么PD应等于什么?
问题导学
例7 已知:如图,AB∥CD,PB和PC分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.求证:PA=PD.
分析
AB∥CD
AD过点P,且与AB垂直
∠BAD+∠CDA= 180°
∠BAD= 90°
∠CDA= 90°
BP平分∠ABC
CP平分∠DCB
PA ⊥ BA
PD⊥ CD
PA =
PD=
归纳
几何证明的方法:综合法
过点P作PE⊥BC于点E
问题导学
为了证明PA=PD,不是直接证明这两条线段相等,而是分别证明它们与哪条线段相等?这种思考方法对你有怎样的启发?
思考
归纳
当图形中没有现成的全等三角形时,
必须通过添加适当的辅助线,构造出所
需要的全等三角形
(p36.3)证明:三角形的两条角平分线的交点到各边的距离相等
已知:如图, △ABC的角平分线BD,CE相交于点P。
求证:点P到三边的距离相等。
证明:过点P做PL⊥AB交AB于点L,过点P做PM⊥BC交BC于点M,过点P做PN⊥AC交AC于点N
∵BP平分∠ABC,且PL⊥AB, PM⊥BC
∴PL=PM
同理可证 PN=PM
即PL=PM=PN
已知:如图, △ABC的角平分线BD,CE相交于点P。
且AB=7,BC=8,AC=9,PM=3,求△ABC的面积
全校A P13 题10
作业本1 P11 题6
问题呈现
思考
已知:如图,AD垂直平分BC,D为垂足.
DM⊥AC,DN⊥AB,M,N分别为垂足.
求证:DM=DN.
从已知条件分析:
(1)AD垂直平分BC,你能得到哪些结论?
(2)DM⊥AC,DN⊥AB,你又能得到哪些结论?
从结论出发分析:
要证明DM=DN,你会想到哪些方法?
思路①:通过证两次三角形全等来得到.
AD垂直平分BC
∠ADC=∠ADB=90°
BD=CD
AD=AD
△ADC≌△ADB
∠CAD=∠BAD
∠C=∠B
△ADM≌△ADN
△MDC≌△NDB
DM=DN
DM=DN
一题多解
(SAS)
(AAS)
(AAS)
思路②:通过证一次全等,再利用
角平分线性质来得到.
△ADC≌△ADB
∠CAD=∠BAD
DM⊥AC,DN⊥AB
DM=DN
一题多解
思路③:利用面积法来得到.
AD垂直平分BC
AB=AC
S△ADC=S△ADB
DM=DN
AB=AC
一题多解
AD是ABC的中线
证明两条线段相等的新方法
——面积法(利用面积相等)
1
当题中出现全等三角形的时候,可以利用全等三角形对应边相等
2
当题中出现角平分线的时候,可以利用角平分线的性质定理
3
当题中具有面积相等的三角形时,可以试试面积法
证明两条线段相等的方法有哪些?
归纳
碰到几何证明题,我们可以如何进行分析呢?
归纳
从已知条件和结论两个角度入手进行分析.
盘点收获
布置作业
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
