有理数的乘方复习
图片预览






文档简介
课件19张PPT。有理数的乘方(复习) 练习一(课前测评)
1、边长为 的正方形的面积为 ;
2、棱长为 的正方体的体积为 ;
3、(-2)×(-2)×(-2)= ;
4、(-1)×(-2)×(-3)×(-4)×5= ;
5、(-1)×(-1)×(-1)×(-1)×(-1)= 。返回下一张上一张退出 -8120-1口答练习一
1)在 中,12是 数,10是
数,读作 ;
2) 的底数是 ,指数是 ,读作 ;
返回下一张上一张退出7的7次方底指12的10次方 3)在 中,-3是 数,16是 数,读作 ; 4)在 中,底数是 ;指数是 ;读作 ;底指-3的16次方17返回下一张上一张退出 的17次方
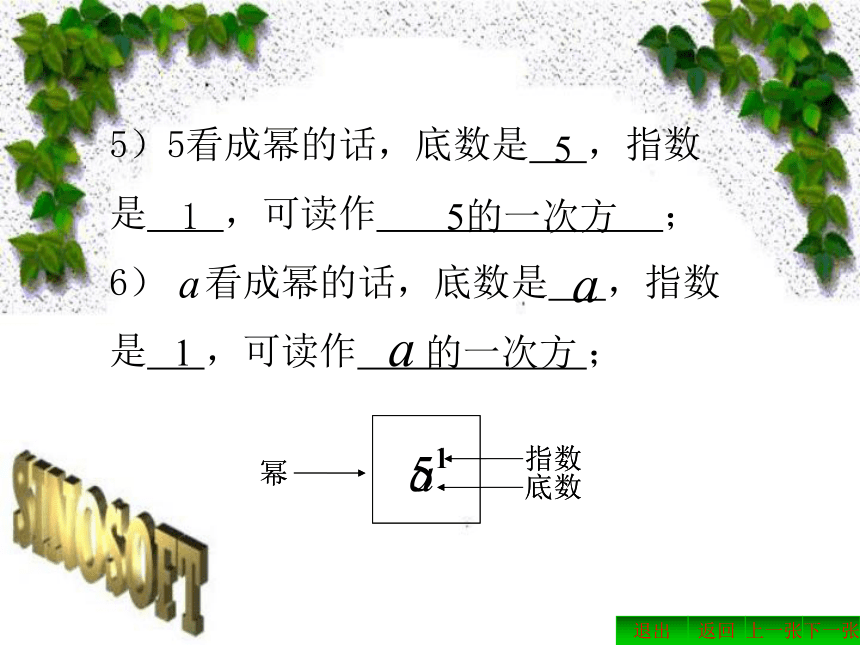
5)5看成幂的话,底数是 ,指数是 ,可读作 ; 6) 看成幂的话,底数是 ,指数是 ,可读作 ; 返回下一张上一张退出515的一次方1的一次方
练习二
一、把下列乘法式子写成乘方的形式:
1、1×1×1×1×1×1×1= ;
2、3×3×3×3×3= ;
3、(-3)×(-3)×(-3)×(-3)= ;
4、 = ;
返回下一张上一张退出二、把下列乘方写成乘法的形式:
1、 = ;
2、 = ;
3、 = ;
返回下一张上一张退出思考:用乘方式子怎么表示 的相反数?练习三
判断下列各题是否正确:
( )① ;
( )② ;
( )③ ;
( )④ ; 返回下一张上一张退出对错错错幂的性质:正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数。返回下一张上一张退出正负 口答练习二
1) 是 (填“正”或“负”)数;
2) 是 (填“正”或“负”)数;
3) = ;
4) = ;11例1计算:
解:思考:例1的两个幂,底数都是负数,为什么这两个幂一个是正数而另一个是负数呢?是由什么数来确定它们的正负呢?当底数是负数时,幂的正负由指数确定,指数是偶数时,幂是正数;指数是奇数时,幂是负数。如果幂的底数正数,那么这个幂有可能是负数吗?不可能!正数的任何次幂是都正数返回下一张上一张退出练习四
计算:
1、 = ; 2、 = ;
3、 = ; 4、 = ;
5、 = ; 6、 = ;
7、 = ; 8、 = .1-125-0.0011-27-1返回下一张上一张退出小结:1、乘方是特殊的乘法运算,所谓特殊就是所乘的因数是相同的;返回下一张上一张退出2、幂是乘方运算的结果;正数的任何次幂是正数,负数的奇次幂是负数,负数的偶次幂是正数;3、进行乘方运算应先定符号后计算。目标检测
1、在 中,底数是 ,指数 ,
2、 读做 ;
3、 的结果是 数(填“正”或“负”);
4、计算: = ;
5、计算: = ;
附加题:计算 。返回下一张上一张退出46-4的7次方或-4的7次幂负-80扩展:1、已知a=355 ,b=444 ,c=533 ,试比较a、b、c的大小解:根据乘方的意义,有a=355 =3*3*3…*3=(3*3*3*3*3)11=2431155个3b=444 =4*4*4…*444个4=(4*4*4*4)11=25611c=533=5*5*5…*5=(5*5*5)11=1251133个5256>243>125即25611 >24311 >12511所以b>a>c退出返回上一张下一张想一想:上述变形的依据是什么?355 = 35*11,444 = 44*11,533 = 53*11。有本例得到这样的一个事实:amn = am*n下一张退出上一张返回扩展:2、计算(-0.25)2002*(-4)2002解:
将成方转为乘法,再根据乘法的规律进行计算(-0.25)2002*(-4)2002
=(-0.25)*(-0.25)*…(-0.25)*(-4)*(-4)*…(-4)2002个-0.25分析:2002个-4=(-0.25)*(-4)*(-0.25)*(-4)*…(-0.25)*(-4)2002个(-0.25)*(-4)=1=1*1*1…*1下一张退出上一张返回想一想:通过上面的计算方法,你能得到那些结论?由本例得到这样的一个事实:ambm =(ab)m(-0.25)2002*(-4)2002=[(-0.25)*(-4)]2002=[1]2002=1下一张退出上一张返回综合练习:退出返回上一张下一张再见!
1、边长为 的正方形的面积为 ;
2、棱长为 的正方体的体积为 ;
3、(-2)×(-2)×(-2)= ;
4、(-1)×(-2)×(-3)×(-4)×5= ;
5、(-1)×(-1)×(-1)×(-1)×(-1)= 。返回下一张上一张退出 -8120-1口答练习一
1)在 中,12是 数,10是
数,读作 ;
2) 的底数是 ,指数是 ,读作 ;
返回下一张上一张退出7的7次方底指12的10次方 3)在 中,-3是 数,16是 数,读作 ; 4)在 中,底数是 ;指数是 ;读作 ;底指-3的16次方17返回下一张上一张退出 的17次方
5)5看成幂的话,底数是 ,指数是 ,可读作 ; 6) 看成幂的话,底数是 ,指数是 ,可读作 ; 返回下一张上一张退出515的一次方1的一次方
练习二
一、把下列乘法式子写成乘方的形式:
1、1×1×1×1×1×1×1= ;
2、3×3×3×3×3= ;
3、(-3)×(-3)×(-3)×(-3)= ;
4、 = ;
返回下一张上一张退出二、把下列乘方写成乘法的形式:
1、 = ;
2、 = ;
3、 = ;
返回下一张上一张退出思考:用乘方式子怎么表示 的相反数?练习三
判断下列各题是否正确:
( )① ;
( )② ;
( )③ ;
( )④ ; 返回下一张上一张退出对错错错幂的性质:正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数。返回下一张上一张退出正负 口答练习二
1) 是 (填“正”或“负”)数;
2) 是 (填“正”或“负”)数;
3) = ;
4) = ;11例1计算:
解:思考:例1的两个幂,底数都是负数,为什么这两个幂一个是正数而另一个是负数呢?是由什么数来确定它们的正负呢?当底数是负数时,幂的正负由指数确定,指数是偶数时,幂是正数;指数是奇数时,幂是负数。如果幂的底数正数,那么这个幂有可能是负数吗?不可能!正数的任何次幂是都正数返回下一张上一张退出练习四
计算:
1、 = ; 2、 = ;
3、 = ; 4、 = ;
5、 = ; 6、 = ;
7、 = ; 8、 = .1-125-0.0011-27-1返回下一张上一张退出小结:1、乘方是特殊的乘法运算,所谓特殊就是所乘的因数是相同的;返回下一张上一张退出2、幂是乘方运算的结果;正数的任何次幂是正数,负数的奇次幂是负数,负数的偶次幂是正数;3、进行乘方运算应先定符号后计算。目标检测
1、在 中,底数是 ,指数 ,
2、 读做 ;
3、 的结果是 数(填“正”或“负”);
4、计算: = ;
5、计算: = ;
附加题:计算 。返回下一张上一张退出46-4的7次方或-4的7次幂负-80扩展:1、已知a=355 ,b=444 ,c=533 ,试比较a、b、c的大小解:根据乘方的意义,有a=355 =3*3*3…*3=(3*3*3*3*3)11=2431155个3b=444 =4*4*4…*444个4=(4*4*4*4)11=25611c=533=5*5*5…*5=(5*5*5)11=1251133个5256>243>125即25611 >24311 >12511所以b>a>c退出返回上一张下一张想一想:上述变形的依据是什么?355 = 35*11,444 = 44*11,533 = 53*11。有本例得到这样的一个事实:amn = am*n下一张退出上一张返回扩展:2、计算(-0.25)2002*(-4)2002解:
将成方转为乘法,再根据乘法的规律进行计算(-0.25)2002*(-4)2002
=(-0.25)*(-0.25)*…(-0.25)*(-4)*(-4)*…(-4)2002个-0.25分析:2002个-4=(-0.25)*(-4)*(-0.25)*(-4)*…(-0.25)*(-4)2002个(-0.25)*(-4)=1=1*1*1…*1下一张退出上一张返回想一想:通过上面的计算方法,你能得到那些结论?由本例得到这样的一个事实:ambm =(ab)m(-0.25)2002*(-4)2002=[(-0.25)*(-4)]2002=[1]2002=1下一张退出上一张返回综合练习:退出返回上一张下一张再见!
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
