4.4 相似三角形的判定 (2)课件 (共16张PPT)
文档属性
| 名称 | 4.4 相似三角形的判定 (2)课件 (共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-18 19:33:24 | ||
图片预览


文档简介
(共16张PPT)
浙教版九年级上册
4.4 相似三角形的判定(2)
第四章 相似三角形
已知:如图,△A'B'C'和 △ABC中,∠A '=∠A,
,求证:△A'B'C' ∽ △ABC
证明:在△ABC 的边AB上截取AD=A'B',过D 作DE∥BC交AC于点E,则△ADE ∽△ABC
AD=A'B'
∴AE=A'C'
又∵∠A '=∠A
∴△ADE≌△A'B'C'
∴ △A'B'C' ∽ △ABC
A'
B'
C'
A
B
C
.
D
E
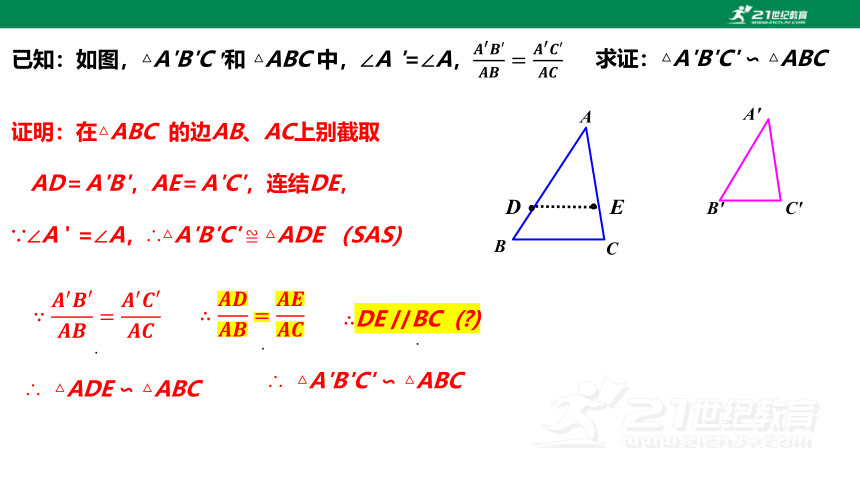
已知:如图,△A'B'C '和 △ABC 中,∠A '=∠A,
求证:△A'B'C' ∽ △ABC
A'
B'
C'
A
B
C
证明:在△ABC 的边AB、AC上别截取
AD=A'B',AE=A'C',连结DE,
∵∠A ' =∠A,∴△A'B'C' ≌ △ADE (SAS)
D
E
∴ △ADE ∽ △ABC
∴ △A'B'C' ∽ △ABC
.
.
DE //BC ( )
.
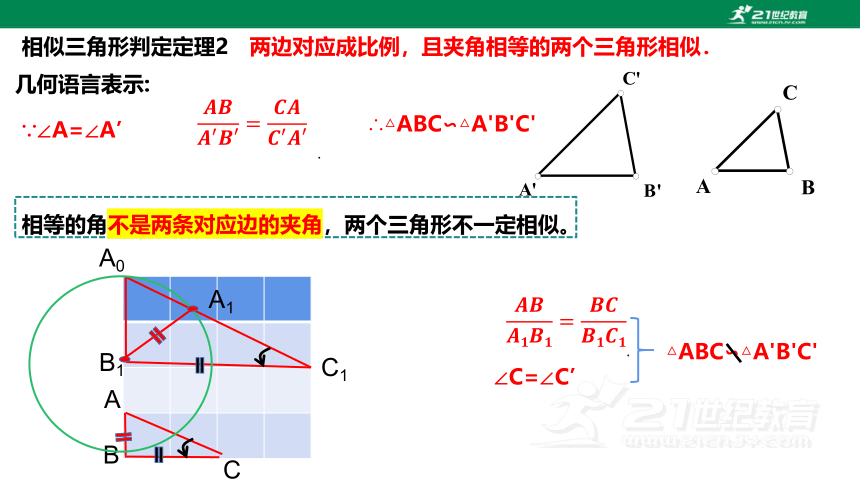
相似三角形判定定理2
两边对应成比例,且夹角相等的两个三角形相似.
几何语言表示:
∵∠A=∠A’
∴△ABC∽△A'B'C'
.
相等的角不是两条对应边的夹角,两个三角形不一定相似。
A
B
C
A0
B1
C1
A1
.
∠C=∠C’
△ABC∽△A'B'C'
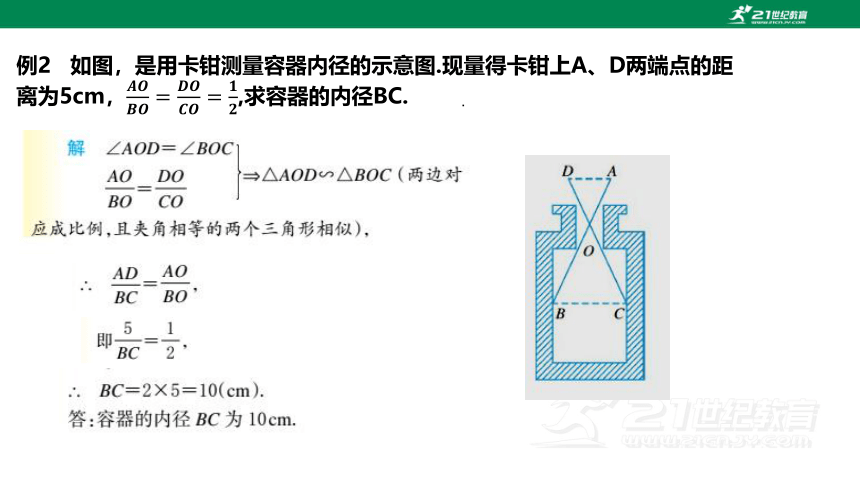
例2 如图,是用卡钳测量容器内径的示意图.现量得卡钳上A、D两端点的距离为5cm,,求容器的内径BC.
.
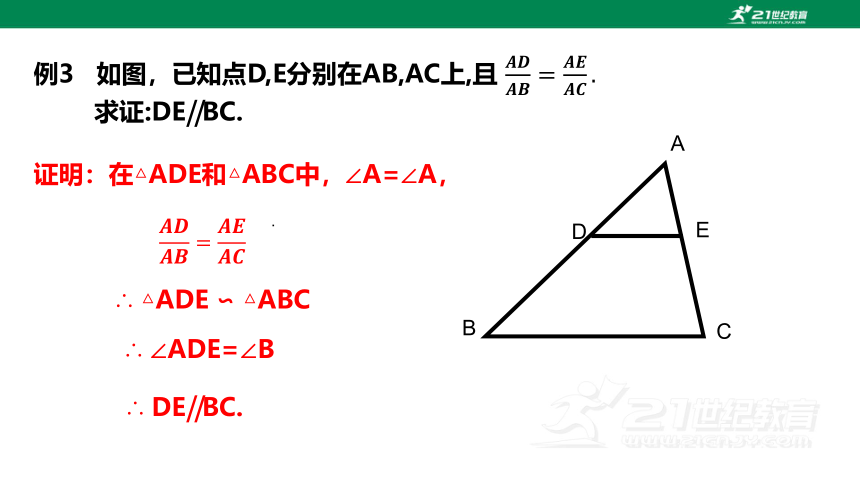
求证:DE‖BC.
例3 如图,已知点D,E分别在AB,AC上,且
D
E
B
C
A
证明:在△ADE和△ABC中,∠A=∠A,
∴ △ADE ∽ △ABC
∴ ∠ADE=∠B
∴ DE‖BC.
.
.
∠AOB=∠COD
△AOB∽△COD
横写
△AOB
△COD
.
竖写
△AOB
△COD
夯实基础,稳扎稳打
.
∠P=∠P
△CPD ∽△BPA.
CD=6
2
=
.
AB 2=AD·AC,
.
∠A=∠A
△ABD ∽△ACB.
∠C =∠ABD=400
3
4. 如图,∠DAB =∠CAE,且 AB · AD = AE·AC,
求证 △ABC ∽△AED.
A
B
C
D
E
证明:∵ AB · AD = AE·AC,
∴
又∵ ∠DAB =∠CAE,
∴∠ DAB +∠BAE =∠CAE +∠BAE ,
即∠DAE =∠BAC,
∴ △ABC ∽△AED.
△ABC
△AED
横找
5.
7.如图,在△ABC中 ,D为边AB 上一点,且AC2=AD·AB,BC2=BD·AB.
求证:CD⊥AB.
证明:∵AC2=AD·AB, ∴=.
∵∠A=∠A, ∴△ACD ∽△ABC.
同理,得△ABC∽△CB D,
∴△ACD∽△ABC∽△CBD, ∴∠ADC=∠CDB.
又∵∠ADC+∠CDB=180°,
∴∠ADC=90°, 即CD⊥AB.
横找
△ABC
△ACD
竖找
△ACD
△ABC
连续递推,豁然开朗
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
浙教版九年级上册
4.4 相似三角形的判定(2)
第四章 相似三角形
已知:如图,△A'B'C'和 △ABC中,∠A '=∠A,
,求证:△A'B'C' ∽ △ABC
证明:在△ABC 的边AB上截取AD=A'B',过D 作DE∥BC交AC于点E,则△ADE ∽△ABC
AD=A'B'
∴AE=A'C'
又∵∠A '=∠A
∴△ADE≌△A'B'C'
∴ △A'B'C' ∽ △ABC
A'
B'
C'
A
B
C
.
D
E
已知:如图,△A'B'C '和 △ABC 中,∠A '=∠A,
求证:△A'B'C' ∽ △ABC
A'
B'
C'
A
B
C
证明:在△ABC 的边AB、AC上别截取
AD=A'B',AE=A'C',连结DE,
∵∠A ' =∠A,∴△A'B'C' ≌ △ADE (SAS)
D
E
∴ △ADE ∽ △ABC
∴ △A'B'C' ∽ △ABC
.
.
DE //BC ( )
.
相似三角形判定定理2
两边对应成比例,且夹角相等的两个三角形相似.
几何语言表示:
∵∠A=∠A’
∴△ABC∽△A'B'C'
.
相等的角不是两条对应边的夹角,两个三角形不一定相似。
A
B
C
A0
B1
C1
A1
.
∠C=∠C’
△ABC∽△A'B'C'
例2 如图,是用卡钳测量容器内径的示意图.现量得卡钳上A、D两端点的距离为5cm,,求容器的内径BC.
.
求证:DE‖BC.
例3 如图,已知点D,E分别在AB,AC上,且
D
E
B
C
A
证明:在△ADE和△ABC中,∠A=∠A,
∴ △ADE ∽ △ABC
∴ ∠ADE=∠B
∴ DE‖BC.
.
.
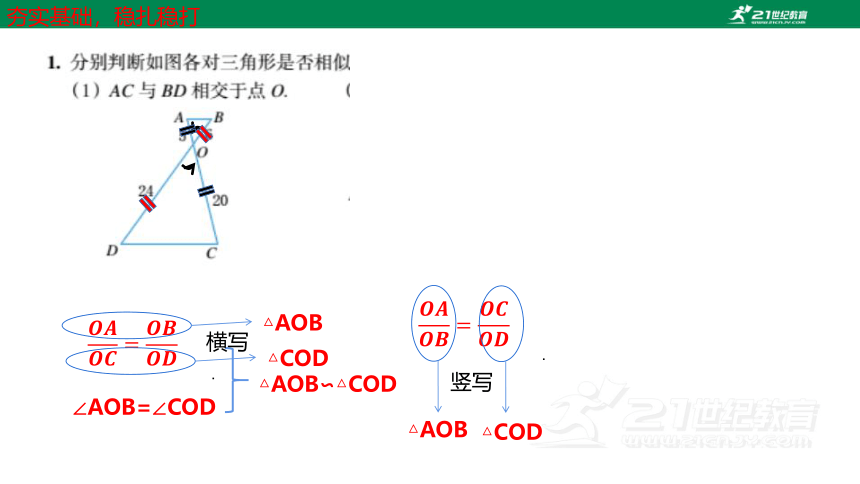
∠AOB=∠COD
△AOB∽△COD
横写
△AOB
△COD
.
竖写
△AOB
△COD
夯实基础,稳扎稳打
.
∠P=∠P
△CPD ∽△BPA.
CD=6
2
=
.
AB 2=AD·AC,
.
∠A=∠A
△ABD ∽△ACB.
∠C =∠ABD=400
3
4. 如图,∠DAB =∠CAE,且 AB · AD = AE·AC,
求证 △ABC ∽△AED.
A
B
C
D
E
证明:∵ AB · AD = AE·AC,
∴
又∵ ∠DAB =∠CAE,
∴∠ DAB +∠BAE =∠CAE +∠BAE ,
即∠DAE =∠BAC,
∴ △ABC ∽△AED.
△ABC
△AED
横找
5.
7.如图,在△ABC中 ,D为边AB 上一点,且AC2=AD·AB,BC2=BD·AB.
求证:CD⊥AB.
证明:∵AC2=AD·AB, ∴=.
∵∠A=∠A, ∴△ACD ∽△ABC.
同理,得△ABC∽△CB D,
∴△ACD∽△ABC∽△CBD, ∴∠ADC=∠CDB.
又∵∠ADC+∠CDB=180°,
∴∠ADC=90°, 即CD⊥AB.
横找
△ABC
△ACD
竖找
△ACD
△ABC
连续递推,豁然开朗
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
