通过建立数学模型解决生活中的实际问题。(浙江省湖州市)
文档属性
| 名称 | 通过建立数学模型解决生活中的实际问题。(浙江省湖州市) |  | |
| 格式 | rar | ||
| 文件大小 | 820.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-12-23 08:58:00 | ||
图片预览




文档简介
(共11张PPT)
吴兴区东林中学 朱锦明
同学们:我们已经学过的函数有哪些呢?
1、一次函数:y=kx+b (k≠0)
2、反比例函数: ( k≠0 )
3、二次函数:一般式y=ax2+bx+c (a≠0)
顶点式y=a(x+m)2+k (a≠0)
交点式y=a(x-x1)(x-x2) (a≠0)
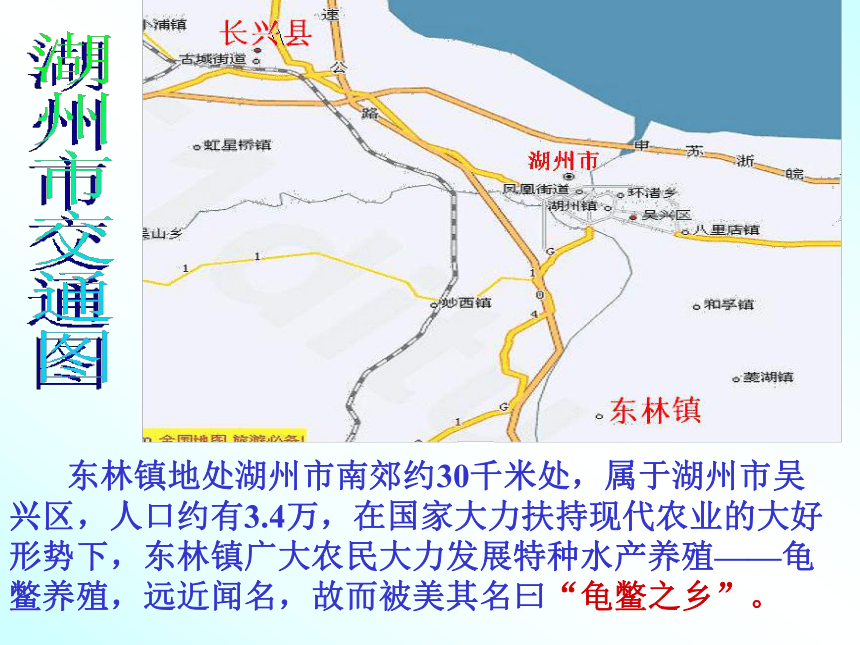
东林镇地处湖州市南郊约30千米处,属于湖州市吴兴区,人口约有3.4万,在国家大力扶持现代农业的大好形势下,东林镇广大农民大力发展特种水产养殖——龟鳖养殖,远近闻名,故而被美其名曰“龟鳖之乡”。
从长兴到东林的路程大约有60km,设巴士车的速度为v km/时,行驶到东林所用时间为t时,但104国道上有限速标志,最大时速不得超过90km/时,根据以上信息,求下列问题。
解(1)路程=时间×速度
vt=60
(0(2)当v=90时,
∵t随v的增大而减小
∴t≥
∴长兴到东林最快需要 小时
(2)求函数t的取值范围,并回答从长兴到东林
最快需多少小时才能到达。
(1)所用时间t与速度v的函数关系式及自变量v
的取值范围。
在参观过程中,刚好遇到有一养殖户新建一个养殖池。该养殖户遇到了一个难题,想利用已有的材料建面积最大的养殖池,想请同学们帮助出出点子,问题如下:
即可列出
自变量的取值范围
S= -2(x2-40x)= -2(x2-40x+400-400)= -2(x-20) 2+800
∵x=20属于0<x<40
养殖池的面积为S m2
分析:设长方形池的宽为x m,则长方形池的长为
x
答:当长方形池的长为40m,宽为20 m时,养殖池面积最大,最大面积为800m2。
养殖户已有砖块可建标准高度且长为240m的围墙,他想用已有的材料建造如下一个长方形的养殖池,要求所建的养殖池的面积最大?并求出最大面积是多少?
∴当x=20时,S最大=800
∴长方形池的长为80-2x=80-2×20=40
得0<x<40
为了给甲鱼池保温,需要在甲鱼池上方建一大棚,大棚横截面形如抛物线,如下图.已知BC=20米,AB=1米,大棚最高处距池底BC2米.为了给大棚加固,需要在距AB,CD4米处各加一根柱子MN和PQ.
O
E
y
x
(1)在图中建立合适的坐标系,并求出相应的抛物线解析式
(2)求加固柱子的高度
解:以AD边所在直线为x轴,以AD的中垂线为y轴,建立坐标系.
由图可知A(-10,0),D(10,0),E(0,1),
设抛物线的解析式为y=a(x+10)(x-10)
将E(0,1)代入解析式,得1=-100a
∴a=-
抛物线解析式为y=- (x+10)(x-10)
=0.64
当x=6时,y=- (x+10)(x-10)
=- × 16×(-4)
∴柱子MN=1+0.64=1.64米
答:柱子MN和PQ的高度为1.64米.
P
Q
M
N
解:(1)设加热时y与x之间的关系式为y=kx+b
养殖甲鱼是一门科学,只有科学养殖,才能取得好的收益。而甲鱼在生长期间很容易受到病菌的感染而得病,所以给甲鱼杀菌消毒是养殖户必做的一项工作。
(2)令y=20,则20=10x+10 ∴x=1
∴
∴消毒的有效时间为 小时。
设停止加热后水温y与时间x的关系式为
∴ k=xy=2× 30=60
∴
(x>2)
解得
∴y=10x+10
(0≤x≤2)
据了解,对甲鱼池消毒用的药物是有温度要求的,药性随温度的变化而变化,一般情况下,该药物在20℃到30℃时药性最佳,对甲鱼池的消毒有较好的效果(我们称为有效温度),已知水池现有的水温为10℃,加热过程中水温y(℃)与加热时间x(小时)之间是一次函数关系,停止加热后水温y与时间x之间成反比例关系,水温与时间的关系如下图:
求(1)水温y与时间x之间的函数关系式。
(2)求此次消毒的有效时间。
y
x
30
0
40
20
10
5
1
2
3
4
2004年,对于东林广大的养殖户来说是一个灾难之年,由于养殖规模空前扩大,成品甲鱼的出产量出现了供大于求的现象,销售价格明显下滑,最低时达到每千克16元,导致全镇所有的养殖户亏损,当地政府于是积极采取措施,成立龟鳖养殖协会,给广大养殖户提供技术和市场信息,信息如下:
信息一,全镇养殖甲鱼的产量y(吨)与销售价格x万元/吨之间有如下关系式:
信息二,每吨成品甲鱼的成本(包括苗种、饲料、水、电等)为2万元/吨
求(1)判断并求出产量y与销售价格x的关系。
(2)全镇产量为多少时,全镇的总利润最大?最大利润为多少?
(3)问产量应控制在什么范围,才能使养殖户有盈利 ?
x
2
2.5
3
3.5
y
4800
4600
4400
4200
解得
(2)设全镇的总利润为W,则
∴产量y=-400x+5600=-400×8+5600=2400吨
∴当全镇产量为2400吨时利润最大,最大
利润为14400万元。
(3)w= -400x2+6400x-11200
令w=0,则-400x2+6400x-11200=0
解得:x1=2, x2=14
∴ 2当x=2时,y=-400x+5600=4800
当x=14时,y=-400x+5600=0
∴y的取值范围是0<y<4800
答:全镇的产量控制在大于0吨,而小于4800吨,可以确保养殖户有盈利。
∴y= -400x+5600
解:(1)设产量y与销售价格x之间的关系为y=kx+b
同学们通过本节课的学习,你学会了什么?
(1)我们已经学过的函数有一次函数,反比例函数
和二次函数,以及这些函数在实际中的应用。
(2)将实际生活问题转化为数学问题。
(5)利用函数的最值解决生活中的最值问题。
(3)找出题中各个变量间的关系,列出函数解析式
(4)通过建立数学模型解决生活中的实际问题。
吴兴区东林中学 朱锦明
同学们:我们已经学过的函数有哪些呢?
1、一次函数:y=kx+b (k≠0)
2、反比例函数: ( k≠0 )
3、二次函数:一般式y=ax2+bx+c (a≠0)
顶点式y=a(x+m)2+k (a≠0)
交点式y=a(x-x1)(x-x2) (a≠0)
东林镇地处湖州市南郊约30千米处,属于湖州市吴兴区,人口约有3.4万,在国家大力扶持现代农业的大好形势下,东林镇广大农民大力发展特种水产养殖——龟鳖养殖,远近闻名,故而被美其名曰“龟鳖之乡”。
从长兴到东林的路程大约有60km,设巴士车的速度为v km/时,行驶到东林所用时间为t时,但104国道上有限速标志,最大时速不得超过90km/时,根据以上信息,求下列问题。
解(1)路程=时间×速度
vt=60
(0
∵t随v的增大而减小
∴t≥
∴长兴到东林最快需要 小时
(2)求函数t的取值范围,并回答从长兴到东林
最快需多少小时才能到达。
(1)所用时间t与速度v的函数关系式及自变量v
的取值范围。
在参观过程中,刚好遇到有一养殖户新建一个养殖池。该养殖户遇到了一个难题,想利用已有的材料建面积最大的养殖池,想请同学们帮助出出点子,问题如下:
即可列出
自变量的取值范围
S= -2(x2-40x)= -2(x2-40x+400-400)= -2(x-20) 2+800
∵x=20属于0<x<40
养殖池的面积为S m2
分析:设长方形池的宽为x m,则长方形池的长为
x
答:当长方形池的长为40m,宽为20 m时,养殖池面积最大,最大面积为800m2。
养殖户已有砖块可建标准高度且长为240m的围墙,他想用已有的材料建造如下一个长方形的养殖池,要求所建的养殖池的面积最大?并求出最大面积是多少?
∴当x=20时,S最大=800
∴长方形池的长为80-2x=80-2×20=40
得0<x<40
为了给甲鱼池保温,需要在甲鱼池上方建一大棚,大棚横截面形如抛物线,如下图.已知BC=20米,AB=1米,大棚最高处距池底BC2米.为了给大棚加固,需要在距AB,CD4米处各加一根柱子MN和PQ.
O
E
y
x
(1)在图中建立合适的坐标系,并求出相应的抛物线解析式
(2)求加固柱子的高度
解:以AD边所在直线为x轴,以AD的中垂线为y轴,建立坐标系.
由图可知A(-10,0),D(10,0),E(0,1),
设抛物线的解析式为y=a(x+10)(x-10)
将E(0,1)代入解析式,得1=-100a
∴a=-
抛物线解析式为y=- (x+10)(x-10)
=0.64
当x=6时,y=- (x+10)(x-10)
=- × 16×(-4)
∴柱子MN=1+0.64=1.64米
答:柱子MN和PQ的高度为1.64米.
P
Q
M
N
解:(1)设加热时y与x之间的关系式为y=kx+b
养殖甲鱼是一门科学,只有科学养殖,才能取得好的收益。而甲鱼在生长期间很容易受到病菌的感染而得病,所以给甲鱼杀菌消毒是养殖户必做的一项工作。
(2)令y=20,则20=10x+10 ∴x=1
∴
∴消毒的有效时间为 小时。
设停止加热后水温y与时间x的关系式为
∴ k=xy=2× 30=60
∴
(x>2)
解得
∴y=10x+10
(0≤x≤2)
据了解,对甲鱼池消毒用的药物是有温度要求的,药性随温度的变化而变化,一般情况下,该药物在20℃到30℃时药性最佳,对甲鱼池的消毒有较好的效果(我们称为有效温度),已知水池现有的水温为10℃,加热过程中水温y(℃)与加热时间x(小时)之间是一次函数关系,停止加热后水温y与时间x之间成反比例关系,水温与时间的关系如下图:
求(1)水温y与时间x之间的函数关系式。
(2)求此次消毒的有效时间。
y
x
30
0
40
20
10
5
1
2
3
4
2004年,对于东林广大的养殖户来说是一个灾难之年,由于养殖规模空前扩大,成品甲鱼的出产量出现了供大于求的现象,销售价格明显下滑,最低时达到每千克16元,导致全镇所有的养殖户亏损,当地政府于是积极采取措施,成立龟鳖养殖协会,给广大养殖户提供技术和市场信息,信息如下:
信息一,全镇养殖甲鱼的产量y(吨)与销售价格x万元/吨之间有如下关系式:
信息二,每吨成品甲鱼的成本(包括苗种、饲料、水、电等)为2万元/吨
求(1)判断并求出产量y与销售价格x的关系。
(2)全镇产量为多少时,全镇的总利润最大?最大利润为多少?
(3)问产量应控制在什么范围,才能使养殖户有盈利 ?
x
2
2.5
3
3.5
y
4800
4600
4400
4200
解得
(2)设全镇的总利润为W,则
∴产量y=-400x+5600=-400×8+5600=2400吨
∴当全镇产量为2400吨时利润最大,最大
利润为14400万元。
(3)w= -400x2+6400x-11200
令w=0,则-400x2+6400x-11200=0
解得:x1=2, x2=14
∴ 2
当x=14时,y=-400x+5600=0
∴y的取值范围是0<y<4800
答:全镇的产量控制在大于0吨,而小于4800吨,可以确保养殖户有盈利。
∴y= -400x+5600
解:(1)设产量y与销售价格x之间的关系为y=kx+b
同学们通过本节课的学习,你学会了什么?
(1)我们已经学过的函数有一次函数,反比例函数
和二次函数,以及这些函数在实际中的应用。
(2)将实际生活问题转化为数学问题。
(5)利用函数的最值解决生活中的最值问题。
(3)找出题中各个变量间的关系,列出函数解析式
(4)通过建立数学模型解决生活中的实际问题。
同课章节目录
