2023—2024学年浙教版数学七年级上册周测十一(5.1-5.3)(含答案)
文档属性
| 名称 | 2023—2024学年浙教版数学七年级上册周测十一(5.1-5.3)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 313.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-19 00:00:00 | ||
图片预览


文档简介
2023-2024学年度第一学期七年级数学(浙教版)周测十一(5.1-5.3)
学校:___________姓名:___________班级:___________考号:___________
一、选择题(共30分)
1.(本题3分)下列方程是一元一次方程的是( )
A. B. C. D.
2.(本题3分)关于的方程的解是,则的值为( ),
A.4 B. C.5 D.
3.(本题3分)在下列方程的变形中,正确的是( )
A.由得 B.由得
C.由得 D.由于得
4.(本题3分)解方程,去分母正确的是( )
A. B.
C. D.
5.(本题3分)根据“x与5的和的3倍比x的少2”列出的方程是( )
A. B.
C. D.
6.(本题3分)有13个乒乓球,有12个质量相同,另有一个较轻一点,如果用天平称,至少称( )次保证能找出这个乒乓球.
A.1 B.2 C.3 D.4
7.(本题3分)解方程时,去分母正确的是( )
A. B.
C. D.
8.(本题3分)已知,则方程的解是( )
A. B. C. D.
9.(本题3分)已知边长为m的正方形面积为12,则下列关于m的说法中:①m是无理数;②m是方程的解;③m是12的算术平方根;④.错误的有( )
A.0个 B.1个 C.2个 D.3个
10.(本题3分)我们规定,对于任意两个有理数,有,如.若,则的值为( )
A. B. C.1 D.0
二、填空题(共16分)
11.(本题4分)下列各式中,是方程的是 (填序号).
① ② ③ ④
12.(本题4分)将方程变形为用含的式子表示,则 .
13.(本题4分)规定一种运算:.例如:.已知,则 .
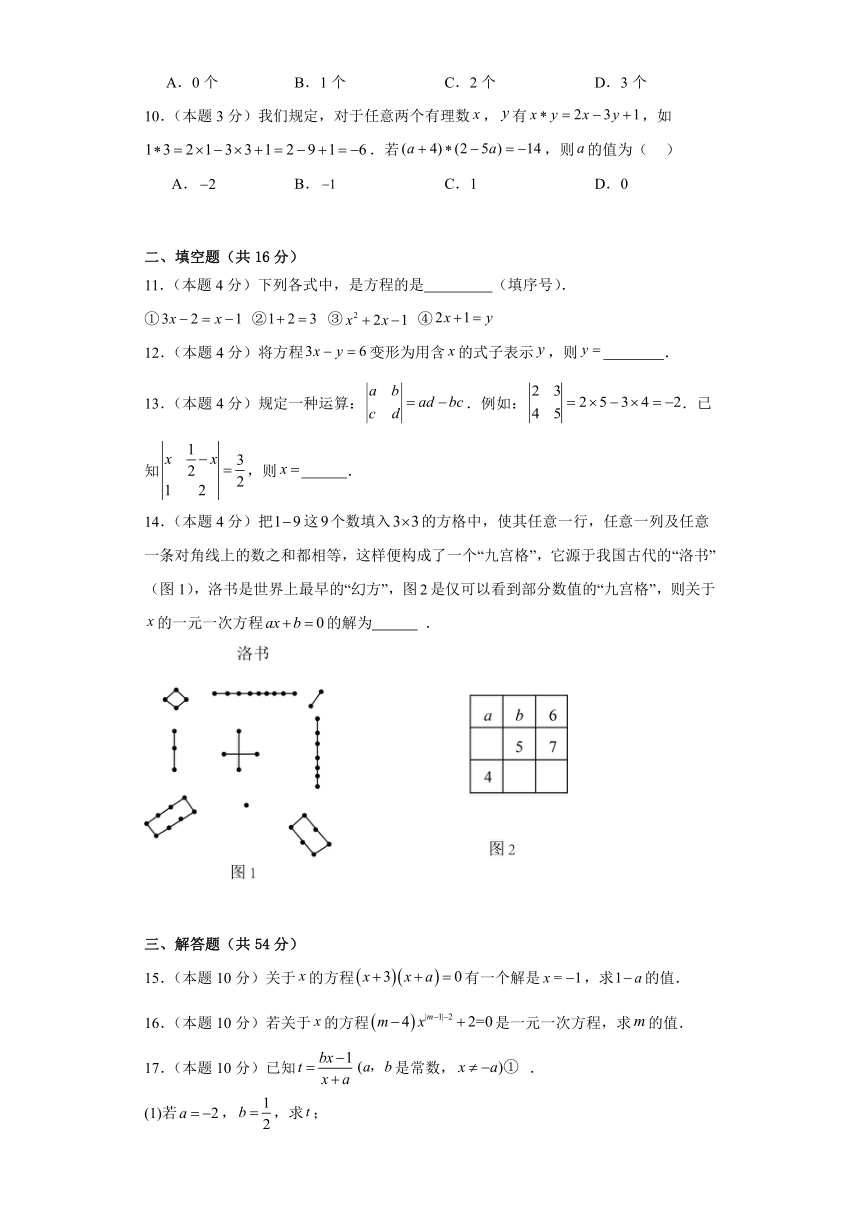
14.(本题4分)把这个数填入的方格中,使其任意一行,任意一列及任意一条对角线上的数之和都相等,这样便构成了一个“九宫格”,它源于我国古代的“洛书”(图1),洛书是世界上最早的“幻方”,图是仅可以看到部分数值的“九宫格”,则关于的一元一次方程的解为 .
三、解答题(共54分)
15.(本题10分)关于的方程有一个解是,求的值.
16.(本题10分)若关于的方程是一元一次方程,求的值.
17.(本题10分)已知是常数, .
(1)若,,求;
(2)试将等式变形成“”形式,其中,表示关于,,的整式;
(3)若的取值与无关,请说明.
18.(本题12分)阅读与思考
阅读以下材料,完成任务.
分子、分母含小数的一元一次方程的解法 我们知道,解一元一次方程的一般步骤是去分母、去括号、移项、合并同类项、系数化为1,那么像这样分子、分母均含有小数的方程如何求出它的解呢?下面是某同学的解答过程: 解:原方程可化为,去分母,得,移项、合并同类项,得,系数化为1,得.
任务:
(1)该同学由变形到是利用了( )
A.等式的基本性质1 B.等式的基本性质2
C.分数的基本性质 D.去分母
(2)请仿照上述方法解方程:.
19.(本题12分)我们常用符号表示小于或者等于x的最大整数.例如,,,.由此可以知道,当x为整数时,.
请根据以上信息,解决下列问题:
(1)______;______;______.
(2)计算并找规律
______;______ ______;______
根据以上计算,可归纳出:
①当x为整数时,______.
②当x不为整数时,______.
(3)计算:
(4)解关于x的方程:
参考答案:
1.C
2.A
3.C
4.B
5.C
6.C
7.D
8.B
9.D
10.B
11.①④
12.
13.
14.
15.解:是方程的一个根,
,
解得,
∴.
16.∵关于x的方程是一元一次方程,
,
解得:.
17.(1)解:当,时,
;
(2)解:将两边都乘以得,
,
去括号得,,
移项得,,
两边都乘以得,,
即,
∴,;
(3)解:∵的取值与无关,
∴,即,
∴,即,
∴.
18.(1)变形到,
是分子与分母乘10,分子与分母乘2,
分式的分子与分母乘(或除以)同一个不等于0的整数,分式的值不变:分式的基本性质
故选:C.
(2)方程可化为
去分母,得,
去括号,得,
移项、合并同类项,得,
系数化为1,得.
19.(1)解:,,.
故答案为:1,,6;
(2),,
,.
根据以上计算,可归纳出:
①当为整数时,.
②当不为整数时,.
故答案为:0,0,,,0,;
(3)
;
(4)由题意,
①当为整数时,,
.
.
.
为整数,
不合题意;
②当是不是整数时,
结果必为整数,
结果必然包含小数,原方程不成立;
综上所述,方程无解.
学校:___________姓名:___________班级:___________考号:___________
一、选择题(共30分)
1.(本题3分)下列方程是一元一次方程的是( )
A. B. C. D.
2.(本题3分)关于的方程的解是,则的值为( ),
A.4 B. C.5 D.
3.(本题3分)在下列方程的变形中,正确的是( )
A.由得 B.由得
C.由得 D.由于得
4.(本题3分)解方程,去分母正确的是( )
A. B.
C. D.
5.(本题3分)根据“x与5的和的3倍比x的少2”列出的方程是( )
A. B.
C. D.
6.(本题3分)有13个乒乓球,有12个质量相同,另有一个较轻一点,如果用天平称,至少称( )次保证能找出这个乒乓球.
A.1 B.2 C.3 D.4
7.(本题3分)解方程时,去分母正确的是( )
A. B.
C. D.
8.(本题3分)已知,则方程的解是( )
A. B. C. D.
9.(本题3分)已知边长为m的正方形面积为12,则下列关于m的说法中:①m是无理数;②m是方程的解;③m是12的算术平方根;④.错误的有( )
A.0个 B.1个 C.2个 D.3个
10.(本题3分)我们规定,对于任意两个有理数,有,如.若,则的值为( )
A. B. C.1 D.0
二、填空题(共16分)
11.(本题4分)下列各式中,是方程的是 (填序号).
① ② ③ ④
12.(本题4分)将方程变形为用含的式子表示,则 .
13.(本题4分)规定一种运算:.例如:.已知,则 .
14.(本题4分)把这个数填入的方格中,使其任意一行,任意一列及任意一条对角线上的数之和都相等,这样便构成了一个“九宫格”,它源于我国古代的“洛书”(图1),洛书是世界上最早的“幻方”,图是仅可以看到部分数值的“九宫格”,则关于的一元一次方程的解为 .
三、解答题(共54分)
15.(本题10分)关于的方程有一个解是,求的值.
16.(本题10分)若关于的方程是一元一次方程,求的值.
17.(本题10分)已知是常数, .
(1)若,,求;
(2)试将等式变形成“”形式,其中,表示关于,,的整式;
(3)若的取值与无关,请说明.
18.(本题12分)阅读与思考
阅读以下材料,完成任务.
分子、分母含小数的一元一次方程的解法 我们知道,解一元一次方程的一般步骤是去分母、去括号、移项、合并同类项、系数化为1,那么像这样分子、分母均含有小数的方程如何求出它的解呢?下面是某同学的解答过程: 解:原方程可化为,去分母,得,移项、合并同类项,得,系数化为1,得.
任务:
(1)该同学由变形到是利用了( )
A.等式的基本性质1 B.等式的基本性质2
C.分数的基本性质 D.去分母
(2)请仿照上述方法解方程:.
19.(本题12分)我们常用符号表示小于或者等于x的最大整数.例如,,,.由此可以知道,当x为整数时,.
请根据以上信息,解决下列问题:
(1)______;______;______.
(2)计算并找规律
______;______ ______;______
根据以上计算,可归纳出:
①当x为整数时,______.
②当x不为整数时,______.
(3)计算:
(4)解关于x的方程:
参考答案:
1.C
2.A
3.C
4.B
5.C
6.C
7.D
8.B
9.D
10.B
11.①④
12.
13.
14.
15.解:是方程的一个根,
,
解得,
∴.
16.∵关于x的方程是一元一次方程,
,
解得:.
17.(1)解:当,时,
;
(2)解:将两边都乘以得,
,
去括号得,,
移项得,,
两边都乘以得,,
即,
∴,;
(3)解:∵的取值与无关,
∴,即,
∴,即,
∴.
18.(1)变形到,
是分子与分母乘10,分子与分母乘2,
分式的分子与分母乘(或除以)同一个不等于0的整数,分式的值不变:分式的基本性质
故选:C.
(2)方程可化为
去分母,得,
去括号,得,
移项、合并同类项,得,
系数化为1,得.
19.(1)解:,,.
故答案为:1,,6;
(2),,
,.
根据以上计算,可归纳出:
①当为整数时,.
②当不为整数时,.
故答案为:0,0,,,0,;
(3)
;
(4)由题意,
①当为整数时,,
.
.
.
为整数,
不合题意;
②当是不是整数时,
结果必为整数,
结果必然包含小数,原方程不成立;
综上所述,方程无解.
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
