4.4 相似三角形的判定(3) 课件(共20张PPT)
文档属性
| 名称 | 4.4 相似三角形的判定(3) 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-19 09:57:10 | ||
图片预览







文档简介
(共20张PPT)
浙教版九年级上册
4.4 相似三角形的判定(3)
第四章 相似三角形
举反例说明:有两边对应成比例的两个三角形不一定相似
3
3
5
5
不相似
温故知新
求证:△ABC∽△A1B1C1.
A
B
C
A1
B1
C1
D
E
证明:在线段(或它的延长线)上截取,
过点D作DE//,交于点E.
证明:三边对应成比例的两个三角形相似.
已知:
.
∴ 1
.
平行截割出相似: ∽△.
.
∴
.
又,
.
∴,
.
∴DE=BC,
.
∴
.
∵△∽△
.
相似三角形的判定方法:
三边对应成比例的两个三角形相似.
符号语言:
∴△ABC∽ △A B C
∵
.
A1
B1
C1
A
B
C
∟
∟
证明:斜边、直角边对应成比例的两个三角形相似.
已知:Rt△ABC、Rt△A1B1C1
.
求证:Rt△ABC∽Rt△A1B1C1.
证明:
.
AB=
.
AC=
.
BC=
.
.
.
=kB1C1
.
∴ Rt△ABC∽Rt△A1B1C1.
∵
.
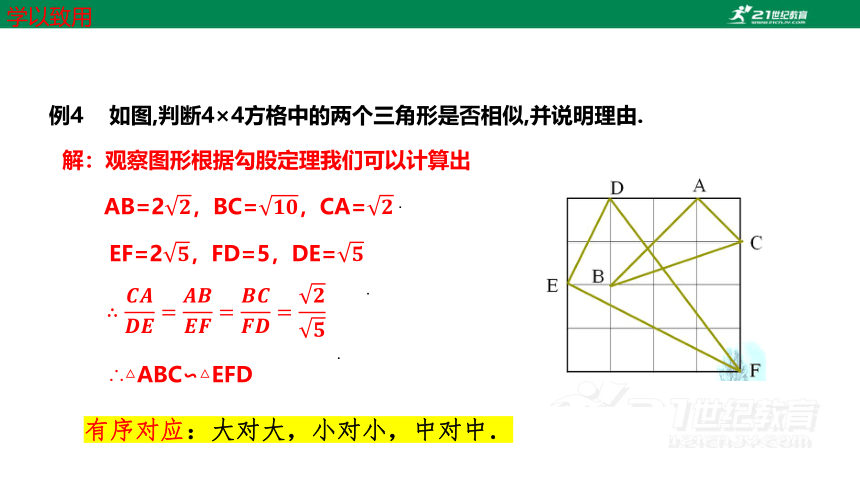
例4 如图,判断4×4方格中的两个三角形是否相似,并说明理由.
解:观察图形根据勾股定理我们可以计算出
AB=2,BC=,CA=
.
EF=2,FD=5,DE=
.
.
∴△ABC∽△EFD
.
有序对应:大对大,小对小,中对中.
学以致用
证明:在△OA’B’与△OAB中,
∴△OA’B’∽△OAB,
∴△A’B’C’ ∽△ABC
例5、已知:如图,O为△ABC内一点,A’,B’,C’分别是OA,OB,OC上的点,且. 求证:△ABC
.
∴,
.
同理可证,
.
∴,
.
同理可证 ,
.
∴,
.
∵∠A’OB’=∠AOB,
.
(两边对应成比例,且夹角相等的两个三角形相似).
中间比
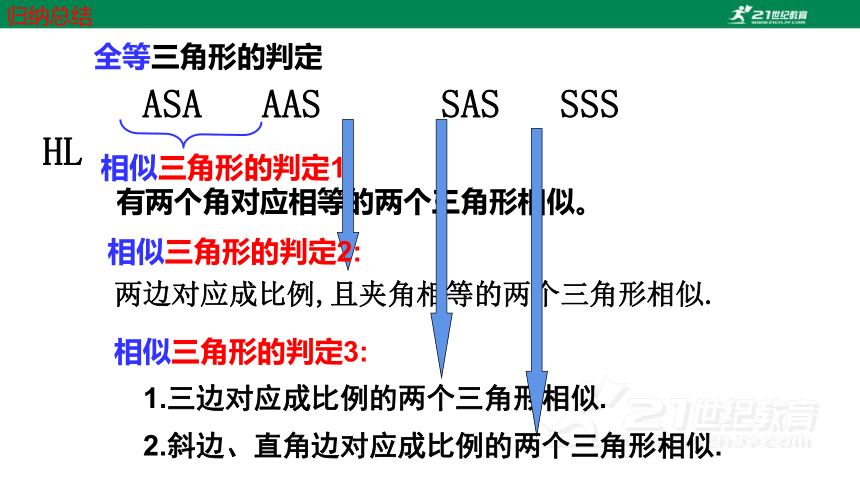
全等三角形的判定
ASA AAS SAS SSS HL
相似三角形的判定1:
有两个角对应相等的两个三角形相似。
两边对应成比例,且夹角相等的两个三角形相似.
相似三角形的判定2:
1.三边对应成比例的两个三角形相似.
相似三角形的判定3:
归纳总结
2.斜边、直角边对应成比例的两个三角形相似.
1.如图, △ABC的三个顶点都在方格纸的格点上。在方格纸内画△ A′B′C′ , 使△A′B′C′ ∽ △ABC,相似比为2:1,且顶点都在格点上。
夯实基础,稳扎稳打
放大
A′
B′
C′
2. 如图, △ABC的三个顶点都在方格纸的格点上。在方格纸内画△A′B′C′ , 使△A′B′C′ ∽ △ABC,相似比为1:2,且顶点都在格点上。
缩小
A′
B′
C′
3. 在△ABC和△A′B′C′中,已知: AB=6cm,BC=8cm,AC=10cm,A′B′=18cm,B′C′=24cm,A′C′=30cm.试证明△ABC与△A′B′C′相似.
证明 ∵
∴
∴ △ABC∽△A′B′C′
(如果一个三角形的三条边和另一个三角形的三条边对应成比例,那么这两个三角形相似).
有序对应:大对大,小对小,中对中.
4. 如图,三个三角形的顶点都在方格纸的格点上。
它们中哪些三角形相似?请说明理由。
△FGM∽△DEB
5.下列条件不能判定△ABC与△ADE相似的是( )
∠CAE=∠BAD
B.∠B=∠ADE,∠CAE=∠BAD
∠C=∠E
D
6. 如图,△ABC中,点 D,E,F 分别是 AB,BC,CA
的中点,求证:△ABC∽△EFD.
证明:∵△ABC中,点D,E,F分别是AB,BC,CA的中点,
∴
∴
∴ △ABC∽△EFD.
7.已知:如图,在△ABC中,点F,O,G在BC边上,点E在AO上,
.
求证:△EFG∽△ABC.
证明:在△OEF 与△OAB中,
∵∠EOF=∠AOB,
.
∴△OEF∽△OAB,
∴,
.
同理可证 ,
.
∴,
.
.
∠1=∠2
∠3=∠4
∴∠1+∠3=∠2+∠4
∠FEG=∠BAC
∴△EFG∽△ABC
1
2
3
4
思维拓展,更上一层
8. 已知:如图, 求证:AB=AE.
B
A
D
E
C
证明:
∴△ADE∽△CAB
∴∠B=∠AEB
∴AB=AE
△ADE
△CAB
横找
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
浙教版九年级上册
4.4 相似三角形的判定(3)
第四章 相似三角形
举反例说明:有两边对应成比例的两个三角形不一定相似
3
3
5
5
不相似
温故知新
求证:△ABC∽△A1B1C1.
A
B
C
A1
B1
C1
D
E
证明:在线段(或它的延长线)上截取,
过点D作DE//,交于点E.
证明:三边对应成比例的两个三角形相似.
已知:
.
∴ 1
.
平行截割出相似: ∽△.
.
∴
.
又,
.
∴,
.
∴DE=BC,
.
∴
.
∵△∽△
.
相似三角形的判定方法:
三边对应成比例的两个三角形相似.
符号语言:
∴△ABC∽ △A B C
∵
.
A1
B1
C1
A
B
C
∟
∟
证明:斜边、直角边对应成比例的两个三角形相似.
已知:Rt△ABC、Rt△A1B1C1
.
求证:Rt△ABC∽Rt△A1B1C1.
证明:
.
AB=
.
AC=
.
BC=
.
.
.
=kB1C1
.
∴ Rt△ABC∽Rt△A1B1C1.
∵
.
例4 如图,判断4×4方格中的两个三角形是否相似,并说明理由.
解:观察图形根据勾股定理我们可以计算出
AB=2,BC=,CA=
.
EF=2,FD=5,DE=
.
.
∴△ABC∽△EFD
.
有序对应:大对大,小对小,中对中.
学以致用
证明:在△OA’B’与△OAB中,
∴△OA’B’∽△OAB,
∴△A’B’C’ ∽△ABC
例5、已知:如图,O为△ABC内一点,A’,B’,C’分别是OA,OB,OC上的点,且. 求证:△ABC
.
∴,
.
同理可证,
.
∴,
.
同理可证 ,
.
∴,
.
∵∠A’OB’=∠AOB,
.
(两边对应成比例,且夹角相等的两个三角形相似).
中间比
全等三角形的判定
ASA AAS SAS SSS HL
相似三角形的判定1:
有两个角对应相等的两个三角形相似。
两边对应成比例,且夹角相等的两个三角形相似.
相似三角形的判定2:
1.三边对应成比例的两个三角形相似.
相似三角形的判定3:
归纳总结
2.斜边、直角边对应成比例的两个三角形相似.
1.如图, △ABC的三个顶点都在方格纸的格点上。在方格纸内画△ A′B′C′ , 使△A′B′C′ ∽ △ABC,相似比为2:1,且顶点都在格点上。
夯实基础,稳扎稳打
放大
A′
B′
C′
2. 如图, △ABC的三个顶点都在方格纸的格点上。在方格纸内画△A′B′C′ , 使△A′B′C′ ∽ △ABC,相似比为1:2,且顶点都在格点上。
缩小
A′
B′
C′
3. 在△ABC和△A′B′C′中,已知: AB=6cm,BC=8cm,AC=10cm,A′B′=18cm,B′C′=24cm,A′C′=30cm.试证明△ABC与△A′B′C′相似.
证明 ∵
∴
∴ △ABC∽△A′B′C′
(如果一个三角形的三条边和另一个三角形的三条边对应成比例,那么这两个三角形相似).
有序对应:大对大,小对小,中对中.
4. 如图,三个三角形的顶点都在方格纸的格点上。
它们中哪些三角形相似?请说明理由。
△FGM∽△DEB
5.下列条件不能判定△ABC与△ADE相似的是( )
∠CAE=∠BAD
B.∠B=∠ADE,∠CAE=∠BAD
∠C=∠E
D
6. 如图,△ABC中,点 D,E,F 分别是 AB,BC,CA
的中点,求证:△ABC∽△EFD.
证明:∵△ABC中,点D,E,F分别是AB,BC,CA的中点,
∴
∴
∴ △ABC∽△EFD.
7.已知:如图,在△ABC中,点F,O,G在BC边上,点E在AO上,
.
求证:△EFG∽△ABC.
证明:在△OEF 与△OAB中,
∵∠EOF=∠AOB,
.
∴△OEF∽△OAB,
∴,
.
同理可证 ,
.
∴,
.
.
∠1=∠2
∠3=∠4
∴∠1+∠3=∠2+∠4
∠FEG=∠BAC
∴△EFG∽△ABC
1
2
3
4
思维拓展,更上一层
8. 已知:如图, 求证:AB=AE.
B
A
D
E
C
证明:
∴△ADE∽△CAB
∴∠B=∠AEB
∴AB=AE
△ADE
△CAB
横找
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
