浙教版八年级上专题1.2 角度计算中的经典模型-重难点题型(含解析)
文档属性
| 名称 | 浙教版八年级上专题1.2 角度计算中的经典模型-重难点题型(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-19 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
角度计算中的经典模型8大题型
【题型1 双垂直模型】
【条件】∠B=∠D=∠ACE=90°.
【结论】∠BAC=∠DCE,∠ACB=∠CED.
【证明】∵∠B=∠D=∠ACE=90°;∴∠BAC+∠ACB=90°;又∠ECD+∠ACB=90°;∴∠BAC=∠DCE
同理,∠ACB+∠DCE =90°,且∠CED+∠DCE =90°;∴∠ACB=∠CED,得证.
【例1】(2020秋 铁西区期中)(1)如图①,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,求证:∠ACD=∠B;
(2)如图②,在Rt△ABC中,∠C=90°,D、E分别在AC,AB上,且∠ADE=∠B,判断△ADE的形状?并说明理由?
(3)如图③,在Rt△ABC和Rt△DBE中,∠C=90°,∠E=90°,点C,B,E在同一直线上,若AB⊥BD,AB=BD,则CE与AC,DE有什么等量关系,并证明.
【变式1-1】(2021春 盐城期末)已知:如图,在△ABC中,∠ACB=90°,CE⊥AB,F为边BC上一点,连接AF交CE于点G,∠CGF=∠CFG.求证:AF平分∠BAC.
【变式1-2】(2020秋 丰城市期中)(1)如图①,△ABC是锐角三角形,高BD,CE相交于点H,找出∠BHC和∠A之间存在何种等量关系;并证明你的结论
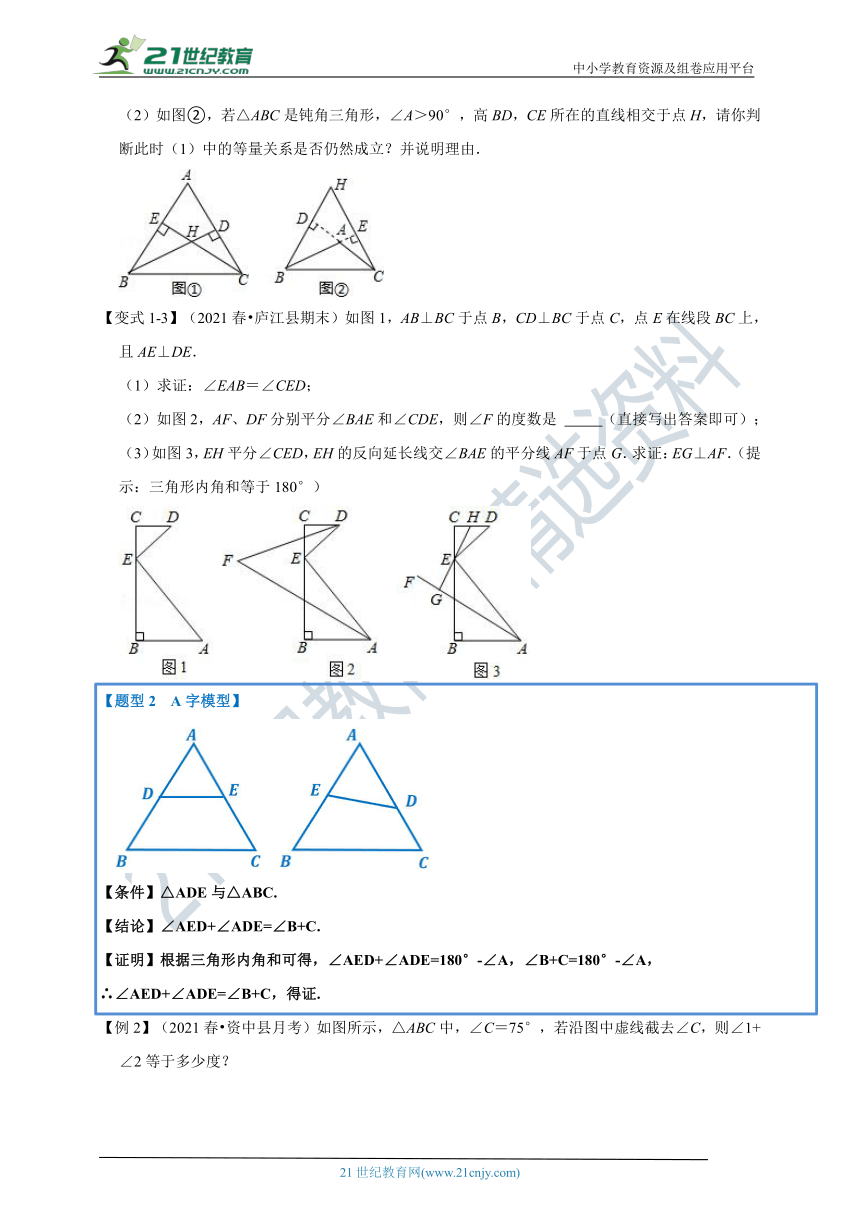
(2)如图②,若△ABC是钝角三角形,∠A>90°,高BD,CE所在的直线相交于点H,请你判断此时(1)中的等量关系是否仍然成立?并说明理由.
【变式1-3】(2021春 庐江县期末)如图1,AB⊥BC于点B,CD⊥BC于点C,点E在线段BC上,且AE⊥DE.
(1)求证:∠EAB=∠CED;
(2)如图2,AF、DF分别平分∠BAE和∠CDE,则∠F的度数是 (直接写出答案即可);
(3)如图3,EH平分∠CED,EH的反向延长线交∠BAE的平分线AF于点G.求证:EG⊥AF.(提示:三角形内角和等于180°)
【题型2 A字模型】
【条件】△ADE与△ABC.
【结论】∠AED+∠ADE=∠B+C.
【证明】根据三角形内角和可得,∠AED+∠ADE=180°-∠A,∠B+C=180°-∠A,
∴∠AED+∠ADE=∠B+C,得证.
【例2】(2021春 资中县月考)如图所示,△ABC中,∠C=75°,若沿图中虚线截去∠C,则∠1+∠2等于多少度?
【变式2-1】(2020春 长沙县校级期中)如图,已知∠A=40°,求∠1+∠2+∠3+∠4的度数.
【变式2-2】(2020春 常州期中)如图,△ABC中,∠B=68°,∠A比∠C大28°,点D、E分别在AB、BC上.连接DE,∠DEB=42°.
(1)求∠A的度数;
(2)判断DE与AC之间的位置关系,并说明理由.
【变式2-3】(2020春 新野县期末)旧知新意:
我们容易证明,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?
尝试探究:
(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?
初步应用:
(2)如图2,在△ABC纸片中剪去△CDE,得到四边形ABDE,∠1=130°,则∠2﹣∠C= ;
(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请利用上面的结论直接写出答案 .
【题型3 8字模型】
【条件】AD、BC相交于点O.
【结论】∠A+∠B=∠C+∠D.(上面两角之和等于下面两角之和)
【证明】在△ABO中,由内角和定理:∠A+∠B+∠BOA=180°,在△CDO中,∠C+∠D+∠COD=180°,
∴∠A+∠B+∠BOA=180°=∠C+∠D+∠COD,由对顶角相等:∠BOA=∠COD
∴∠A+∠B=∠C+∠D,得证.
【例3】(2020秋 庆阳期中)【问题背景】(1)如图1的图形我们把它称为“8字形”,请说明∠A+∠B=∠C+∠D;
【问题探究】
(2)如图2,直线AP平分△BAO的外角∠FAD,CP平分△OCD的外角∠BCE,若∠ABC=32°,∠ADC=22°,求∠P的度数.
【变式3-1】(2021春 江阴市校级月考)如图1,已知线段AB、CD相交于点O,连接AC、BD,则我们把形如这样的图形称为“8字型”.
(1)求证:∠A+∠C=∠B+∠D;
(2)如图2,若∠CAB和∠BDC的平分线AP和DP相交于点P,与CD、AB分别相交于点M、N.
①以线段AC为边的“8字型”有 个,以点O为交点的“8字型”有 个;
②若∠B=100°,∠C=120°,求∠P的度数;
③若角平分线中角的关系改为“∠CAB=3∠CAP,∠CDB=3∠CDP”,试探究∠P与∠B、∠C之间存在的数量关系,并证明理由.
【变式3-2】(2021春 侯马市期末)(1)已知:如图①的图形我们把它称为“8字形”,试说明:∠A+∠B=∠C+∠D.
(2)如图②,AP,CP分别平分∠BAD,∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的度数.
(3)如图(3),直线AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的数量关系是 ;
(4)如图(4),直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的数量关系是 .
【变式3-3】(2021春 高新区校级月考)(1)如图1的图形我们把它称为“8字形”,请说明:∠A+∠B=∠C+∠D.
(2)阅读下面的内容,并解决后面的问题:
(①)如图2,AP、CP分别平分∠BAD、∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的度数.
(②)如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想∠P的度数,并说明理由.
(③)如图4中,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论,无需说明理由.
【题型4 飞镖模型】
【条件】四边形ABDC如上左图所示.
【结论】∠D=∠A+∠B+∠C.(凹四边形凹外角等于三个内角和)
【证明】如上右图,连接AD并延长到E,则:
∠BDC=∠BDE+∠CDE=(∠B+∠1)+(∠2+∠C)=∠B+∠BAC+∠C.本质为两个三角形外角和定理证明.
【例4】(2020春 汝阳县期末)阅读下列材料,然后解答后面的问题.
(1)定义:把四边形的某些边向两方延长,其他各边有不在延长所得直线的同一旁,这样的四边形叫做凹四边形.如图1,四边形ABCD为凹四边形.
(2)性质探究:请完成凹四边形一个性质的证明.
已知:如图2,四边形ABCD是凹四边形.
求证:∠BCD=∠B+∠A+∠D.
(3)性质应用:
如图3,在凹四边形ABCD中,∠BAD的角平分线与∠BCD的角平分线交于点E,若∠ADC=140°,∠AEC=102°,则∠B= °.
【变式4-1】(2020秋 白银期末)(1)探究:如图1,求证:∠BOC=∠A+∠B+∠C.
(2)应用:如图2,∠ABC=100°,∠DEF=130°,求∠A+∠C+∠D+∠F的度数.
【变式4-2】(2020秋 黄石港区校级期中)如图,(1)求证:∠ABC=∠A+∠C+∠ADC;
(2)若∠A=52°,∠C=20°,BE、DE分别平分∠ABC和∠ADC,交于点E,求∠E的度数.
【变式4-3】(2020春 福山区期中)直线在同一平面内有平行和相交两种位置关系,线段首尾连接可以变换出很多不同的图形,这些不同的角又有很多不同关系,今天我们就来探究一下这些奇妙的图形吧!
【问题探究】
(1)如图1,请直接写出∠A+∠B+∠C+∠D+∠E= ;
(2)将图1变形为图2,∠A+∠DBE+∠C+∠D+∠E的结果如何?请写出证明过程;
(3)将图1变形为图3,则∠A+∠B+∠C+∠D+∠E的结果如何?请写出证明过程.
【变式拓展】
(4)将图3变形为图4,已知∠BGF=160°,那么∠A+∠B+∠C+∠D+∠E+∠F的度数是 .
【题型5 风筝模型】
【条件】四边形ABPC,分别延长AB、AC于点D、E,如上左图所示.
【结论】∠PBD+∠PCE=∠A+∠P.
【证明】如上右图,连接AP,则:∠PBD=∠PAB+∠APB,∠PCE=∠PAC+∠APC,
∴∠PBD+∠PCE=∠PAB+∠APB+∠PAC+∠APC=∠BAC+∠BPC,得证.
【例5】(2020春 灌云县期中)如图,将△ABC的一角折叠,使点C落在△ABC内一点
(1)若∠1=40°,∠2=30°,求∠C的度数;
(2)试通过第(1)问,直接写出∠1、∠2、∠C三者之间的关系.
【变式5-1】(2020秋 路北区期中)如图,在△ABC中,D、E分别是边AB、AC上一点,将△ABC沿DE折叠,使点A落在边BC上.若∠A=55°,求∠1+∠2+∠3+∠4四个角和的度数?
【变式5-2】(2020春 迁安市期末)动手操作:
一个三角形的纸片ABC,沿DE折叠,使点A落在点Aˊ处.
观察猜想
(1)如图1,若∠A=40°,则∠1+∠2= °;
若∠A=55°,则∠1+∠2= °;
若∠A=n°,则∠1+∠2= °.
探索证明:
(2)利用图1,探索∠1、∠2与∠A有怎样的关系?请说明理由.
拓展应用
(3)如图2,把△ABC折叠后,BA′平分∠ABC,CA′平分∠ACB,若∠1+∠2=108°,利用(2)中结论求∠BA′C的度数.
【变式5-3】(2021春 高邮市校级期末)直角△ABC中,∠C=90°,点D,E分别是边AC,BC上的点,点P是一动点,令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在线段AB上,如图1所示,且∠α=50°,则∠1+∠2= ;
(2)若点P在边AB上运动,如图2所示,则∠α、∠1、∠2之间有何关系,并说明理由;
(3)如图3,若点P在斜边BA的延长线上运动(CE<CD),请写出∠α、∠1、∠2之间的关系式.
【题型6 两内角角平分线模型】
【条件】△ABC中,BI、CI分别是∠ABC和∠ACB的角平分线,且相交于点I.
【结论】
【证明】∵BI是∠ABC平分线,∴∵CI是∠ACB平分线,∴
由A→B→I→C→A的飞镖模型可知:
∠I=∠A+∠2+∠3=∠A++=∠A+=.
【例6】(2020春 兴化市月考)如图,△ABC的角平分线BD、CE相交于点P.
(1)若∠ABC=50°,∠ACB=70°,则∠A= °;
(2)若∠A=80°,试求∠BPC的度数;
(3)试直接写出∠DPC与∠A之间的数量关系:∠DPC= .
【变式6-1】(2020秋 硚口区期中)如图,在Rt△ABC中,∠C=90°,BD平分∠ABC交AC于点D,AP平分∠BAC交BD于点P,∠BDC=58°,求∠BAP的度数.
【变式6-2】(2020春 浦东新区期末)如图,点A、B分别在射线ON、OM上运动(不与点O重合),AC、BC分别是∠BAO和∠ABO的角平分线,BC延长线交ON于点G.
(1)若∠MON=60°,则∠ACB= °;若∠MON=90°,则∠ACB= °;
(2)若∠MON=n°.请求出∠ACG的度数;(用含n的代数式表示)
【变式6-3】(2020春 南岗区期末)已知在△ABC中,∠A=100°,点D在△ABC的内部连接BD,CD,且∠ABD=∠CBD,∠ACD=∠BCD.
(1)如图1,求∠BDC的度数;
(2)如图2,延长BD交AC于点E,延长CD交AB于点F,若∠AED﹣∠AFD=12°,求∠ACF的度数.
【题型7 两外角角平分线模型】
【条件】△ABC中,BI、CI分别是△ABC的外角的角平分线,且相交于点O.
【结论】.
【证明】∵BO是∠EBC平分线,∴,∵CO是∠FCB平分线,∴
由△BCO中内角和定理可知:∠O=180°-∠2 -∠5 =180°--=180°--===.
【例7】(2020春 浦东新区期末)已知:如图,△ABC的两个外角的平分线交于点P,如果∠A=40°,求∠BPC的度数.
【变式7-1】(2020秋 鄂伦春自治旗月考)如图,△ABC中,分别延长△ABC的边AB、AC到D、E,∠CBD与∠BCE的平分线相交于点P,爱动脑筋的小明在写作业的时发现如下规律:
(1)若∠A=60°,则∠P= °;
(2)若∠A=40°,则∠P= °;
(3)若∠A=100°,则∠P= °;
(4)请你用数学表达式归纳∠A与∠P的关系 .
【变式7-2】(2020春 石城县期末)如图,在四边形ABCD中,AD∥BC,∠B=∠D,延长BA至点E,连接CE,且CE交AD于点F,∠EAD和∠ECD的角平分线相交于点P.
(1)①直接写出AB和CD的位置关系: ;
②求证:∠EAD∠ECD=∠APC.
(2)若∠B=70°,∠E=60°,求∠APC的度数;
(3)若∠APC=m°,∠EFD=n°,请你探究m和n之间的数量关系.
【变式7-3】(2021春 东坡区校级期末)如图,四边形ABCD,BE、DF分别平分四边形的外角∠MBC和∠NDC,若∠BAD=α,∠BCD=β.
(1)如图1,若α+β=120°,求∠MBC+∠NDC的度数;
(2)如图1,若BE与DF相交于点G,∠BGD=30°,请写出α、β所满足的等量关系式;
(3)如图2,若α=β,判断BE、DF的位置关系,并说明理由.
【题型8 内外角角平分线模型】
【条件】△ABC中,BP、CP分别是△ABC的内角和外角的角平分线,且相交于点P.
【结论】
【证明】 ∵BP是∠ABC平分线,∴ ∵CP是∠ACE平分线,∴
由△ABC外角定理可知:∠ACE=∠ABC+∠A即:2∠1=2∠3+∠A ……①
对①式两边同时除以2,得:∠1=∠3+ ……②又在△BPC中由外角定理可知:∠1=∠3+∠P ……③
比较②③式子可知:.==.
【例8】(2021春 靖江市校级月考)如图①,△ABC中,BD平分∠ABC,且与△ABC的外角∠ACE的角平分线交于点D.
(1)若∠ABC=70°,∠ACB=40°,求∠D的度数;
(2)若把∠A截去,得到四边形MNCB,如图②,猜想∠D、∠M、∠N的关系,并说明理由.
【变式8-1】(2020春 兴化市期中)(1)思考探究:如图,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,已知∠ABC=70°,∠ACD=100°.求∠A和∠P的度数;
(2)类比探究:如图,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,已知∠P=n°.求∠A的度数(用含n的式子表示);
(3)拓展迁移:已知,在四边形ABCD中,四边形ABCD的内角∠ABC与外角∠DCE的平分线所在直线相交于点P,∠P=n°,请画出图形;并探究出∠A+∠D的度数(用含n的式子表示).
【变式8-2】(2020秋 平舆县期中)已知:如图,∠MON=90°,点A、B分别在射线OM、ON上移动(不与点O重合),AC平分∠MAB,AC的反向延长线与∠ABO的平分线相交于点D.
(1)当∠ABO=70°时、∠D的度数是多少?
(2)随着点A、B的移动,试问∠D的大小是否变化?请说出你的理由.
【变式8-3】(2020春 惠安县期末)在△ABC中,∠ACB的平分线CD与外角∠EAC的平分线AF所在的直线交于点D.
(1)如图1,若∠B=60°,求∠D的度数;
(2)如图2,把△ACD沿AC翻折,点D落在D′处.
①当AD′⊥AD时,求∠BAC的度数;
②试确定∠DAD′与∠BAC的数量关系,并说明理由.
角度计算中的经典模型
【题型1 双垂直模型】
【条件】∠B=∠D=∠ACE=90°.
【结论】∠BAC=∠DCE,∠ACB=∠CED.
【证明】∵∠B=∠D=∠ACE=90°;∴∠BAC+∠ACB=90°;又∠ECD+∠ACB=90°;∴∠BAC=∠DCE
同理,∠ACB+∠DCE =90°,且∠CED+∠DCE =90°;∴∠ACB=∠CED,得证.
【例1】(2020秋 铁西区期中)(1)如图①,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,求证:∠ACD=∠B;
(2)如图②,在Rt△ABC中,∠C=90°,D、E分别在AC,AB上,且∠ADE=∠B,判断△ADE的形状?并说明理由?
(3)如图③,在Rt△ABC和Rt△DBE中,∠C=90°,∠E=90°,点C,B,E在同一直线上,若AB⊥BD,AB=BD,则CE与AC,DE有什么等量关系,并证明.
【解题思路】(1)根据直角三角形的性质得出∠ACD+∠A=∠B+∠DCB=90°,再解答即可;
(2)根据直角三角形的性质得出∠ADE+∠A=∠A+∠B=90°,再解答即可;
(3)根据直角三角形的性质得出∠ABC+∠A=∠ABC+∠DBE=∠DBE+∠D=90°,再解答即可.
【解答过程】证明:(1)∵在Rt△ABC中,∠ACB=90°,CD⊥AB,
∴∠ACD+∠A=∠B+∠DCB=90°,
∴∠ACD=∠B;
(2)△ADE是直角三角形.
∵在Rt△ABC中,∠C=90°,D、E分别在AC,AB上,且∠ADE=∠B,∠A为公共角,
∴∠AED=∠ACB=90°,
∴△ADE是直角三角形;
(3)CE=AC+DE,理由如下:
∵在Rt△ABC和Rt△DBE中,∠C=90°,∠E=90°,AB⊥BD,
∴∠ABC+∠A=∠ABC+∠DBE=∠DBE+∠D=90°,
∴∠A=∠DBE,∠ABC=∠BDE,
在△ABC与△BDE中
,
∴△ABC≌△BDE(ASA),
∴CB=DE,BE=AC,
∴CE=BC+BE=AC+DE;
【变式1-1】(2021春 盐城期末)已知:如图,在△ABC中,∠ACB=90°,CE⊥AB,F为边BC上一点,连接AF交CE于点G,∠CGF=∠CFG.求证:AF平分∠BAC.
【解题思路】由三角形的内角和定理结合垂直的定义可求得∠CAF+∠CFG=90°,∠AGE+∠FAE=90°,进而可得∠CAF=∠FAE,即可证明结论.
【解答过程】解:∵∠ACB=90°,∠CAF+∠ACB+∠CFG=180°,
∴∠CAF+∠CFG=90°,
∵CE⊥AB,
∴∠AEC=90°,
∵∠AEC+∠AGE+∠FAE=180°,
∴∠AGE+∠FAE=90°,
∵∠AGE=∠CGF=∠CFG,
∴∠CAF=∠FAE,
∴AF平分∠BAC.
【变式1-2】(2020秋 丰城市期中)(1)如图①,△ABC是锐角三角形,高BD,CE相交于点H,找出∠BHC和∠A之间存在何种等量关系;并证明你的结论
(2)如图②,若△ABC是钝角三角形,∠A>90°,高BD,CE所在的直线相交于点H,请你判断此时(1)中的等量关系是否仍然成立?并说明理由.
【解题思路】(1)根据对顶角的性质,可得∠BHC与∠EHD的关系,根据四边形的内角和定理,可得答案;
(2)根据对顶角的性质,可得∠BHC与∠EHD的关系,根据四边形的内角和定理,可得答案.
【解答过程】解:(1)∵BD⊥AC,
∴∠ADB=90°,
∵CE⊥AB,
∴∠AEC=90°,
∵∠A+∠ADB+∠AEC+∠DHE=360°,
∴∠DHE=360﹣(∠A+∠ADB+∠AEC)=360﹣(∠A+90+90)=180﹣∠A
∴∠BHC=∠DHE=180﹣∠A
(2)∵BD⊥AC,
∴∠ADH=90°
∵CE⊥AB,
∴∠AEH=90°
∵∠DAE+∠ADH+∠AEH+∠BHC=360
∴∠BHC=360﹣(∠DAE+∠ADH+∠AEH)=360﹣(∠DAE+90+90)=180﹣∠DAE
∴∠BHC=180﹣∠A
【变式1-3】(2021春 庐江县期末)如图1,AB⊥BC于点B,CD⊥BC于点C,点E在线段BC上,且AE⊥DE.
(1)求证:∠EAB=∠CED;
(2)如图2,AF、DF分别平分∠BAE和∠CDE,则∠F的度数是 (直接写出答案即可);
(3)如图3,EH平分∠CED,EH的反向延长线交∠BAE的平分线AF于点G.求证:EG⊥AF.(提示:三角形内角和等于180°)
【解题思路】(1)根据垂直得到直角三角形,由直角三角形两锐角互余利用等量代换证明结论;
(2)通过作FM∥AB∥CD可证∠DFA=∠CDF+∠BAF,因为∠CDE+∠BAE=90°和角平分线的定义可得∠F(∠CDE+∠BAE),继而得到答案;
(3)根据角平分线的定义得∠CEH=∠DEH=∠GEB=∠BAG=∠EAF,由于∠B=90°,∠BAE+∠BEA=90°,在△AEG中,可证得∠EAG+∠AEG=90°,从而证得结论.
【解答过程】(1)证明:∵AB⊥BC,CD⊥BC,
∴∠B=∠C=90°,
∴∠BAE+∠AEB=90°,
∵AE⊥DE,
∴∠AED=90°,
∴∠AEB+∠CED=90°,
∴∠BAE=∠CED.
(2)解:答案为45°;
过点F作FM∥AB,如图,
∵AB⊥BC,CD⊥BC,
∴∠B=∠C=90°,
∴AB∥CD,
∵∠C=90°,
∴∠CED+∠CDE=90°,
∵∠BAE=∠CED,
∴∠BAE+∠CDE=90°,
∵AF、DF分别平分∠BAE和∠CDE,
∴∠CDF∠CDE,∠BAF∠BAE,
∴∠CDF+∠BAF(∠BAE+∠CDE)=45°,
∵FM∥AB∥CD,
∴∠CDF=∠DFM,∠BAF=∠AFM,
∴∠AFD=∠CDF+∠BAF=45°.
(3)∵EH平分∠CED,
∴∠CEH∠CED,
∴∠BEG∠CED,
∵AF平分∠BAE,
∴∠BAG∠BAE,
∵∠BAE=∠CED,
∴∠BAG=∠BEG,
∵∠BAE+∠BEA=90°,
∴∠BAG+∠GAE+∠AEB=90°,
即∠GAE+∠AEB+∠BEG=90°,
∴∠AGE=90°,
∴EG⊥AF.
【题型2 A字模型】
【条件】△ADE与△ABC.
【结论】∠AED+∠ADE=∠B+C.
【证明】根据三角形内角和可得,∠AED+∠ADE=180°-∠A,∠B+C=180°-∠A,
∴∠AED+∠ADE=∠B+C,得证.
【例2】(2021春 资中县月考)如图所示,△ABC中,∠C=75°,若沿图中虚线截去∠C,则∠1+∠2等于多少度?
【解题思路】根据三角形内角和定理求出∠A+∠B,根据多边形的内角和公式求出即可.
【解答过程】解:∵∠A+∠B+∠C=180°,
∴∠A+∠B=180°﹣∠C,
∵∠C=75°,
∴∠A+∠B=180°﹣75°=105°,
∵∠1+∠2+∠A+∠B=360°,
∴∠1+∠2=360°﹣(∠A+∠B),
∴∠1+∠2=360°﹣105°=255°.
【变式2-1】(2020春 长沙县校级期中)如图,已知∠A=40°,求∠1+∠2+∠3+∠4的度数.
【解题思路】根据三角形的内角和定理分别求得∠1+∠2,∠3+∠4,就可求得最后结果.
【解答过程】解:∵∠A=40°,
∴∠1+∠2=∠3+∠4=180°﹣∠A=140°.
∴∠1+∠2+∠3+∠4=280°.
【变式2-2】(2020春 常州期中)如图,△ABC中,∠B=68°,∠A比∠C大28°,点D、E分别在AB、BC上.连接DE,∠DEB=42°.
(1)求∠A的度数;
(2)判断DE与AC之间的位置关系,并说明理由.
【解题思路】(1)设∠C的度数为x,根据三角形的内角和列出方程解答即可;
(2)根据平行线的判定解答即可.
【解答过程】解:(1)设∠C的度数为x°,则∠A的度数为(x+28)°,
△ABC中,∠A+∠B+∠C=180°,∠B=68°,
可得:x+x+28+68=180,
解得:x=42,
所以∠C=42°,∠A=70°,
(2)∵∠DEB=42°,∠C=42°,
∴∠DEB=∠C,
∴DE∥AC.
【变式2-3】(2020春 新野县期末)旧知新意:
我们容易证明,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?
尝试探究:
(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?
初步应用:
(2)如图2,在△ABC纸片中剪去△CDE,得到四边形ABDE,∠1=130°,则∠2﹣∠C= ;
(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请利用上面的结论直接写出答案 .
【解题思路】(1)根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠DBC+∠ECB,再利用三角形内角和定理整理即可得解;
(2)根据(1)的结论整理计算即可得解;
(3)表示出∠DBC+∠ECB,再根据角平分线的定义求出∠PBC+∠PCB,然后利用三角形内角和定理列式整理即可得解;
【解答过程】解:(1)∠DBC+∠ECB
=180°﹣∠ABC+180°﹣∠ACB
=360°﹣(∠ABC+∠ACB)
=360°﹣(180°﹣∠A)
=180°+∠A;
(2)∵∠1+∠2=∠180°+∠C,
∴130°+∠2=180°+∠C,
∴∠2﹣∠C=50°;
(3)∠DBC+∠ECB=180°+∠A,
∵BP、CP分别平分外角∠DBC、∠ECB,
∴∠PBC+∠PCB(∠DBC+∠ECB)(180°+∠A),
在△PBC中,∠P=180°(180°+∠A)=90°∠A;
即∠P=90°∠A;
故答案为:50°,∠P=90°∠A;
【题型3 8字模型】
【条件】AD、BC相交于点O.
【结论】∠A+∠B=∠C+∠D.(上面两角之和等于下面两角之和)
【证明】在△ABO中,由内角和定理:∠A+∠B+∠BOA=180°,在△CDO中,∠C+∠D+∠COD=180°,
∴∠A+∠B+∠BOA=180°=∠C+∠D+∠COD,由对顶角相等:∠BOA=∠COD
∴∠A+∠B=∠C+∠D,得证.
【例3】(2020秋 庆阳期中)【问题背景】(1)如图1的图形我们把它称为“8字形”,请说明∠A+∠B=∠C+∠D;
【问题探究】
(2)如图2,直线AP平分△BAO的外角∠FAD,CP平分△OCD的外角∠BCE,若∠ABC=32°,∠ADC=22°,求∠P的度数.
【解题思路】(1)根据三角形内角和定理即可证明.
(2)由AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,推出∠1=∠2,∠3=∠4,推出∠PAD=180°﹣∠2,∠PCD=180°﹣∠3,由∠P+(180°﹣∠1)=∠D+(180°﹣∠3),∠P+∠1=∠B+∠4,推出2∠P=∠B+∠D,即可解决问题.
【解答过程】(1)证明:在△AOB中,∠A+∠B+∠AOB=180°,
在△COD中,∠C+∠D+∠COD=180°,
∵∠AOB=∠COD,
∴∠A+∠B=∠C+∠D;
(2)如图2,
∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,
∴∠1=∠2,∠3=∠4,
∴∠PAD=180°﹣∠2,∠PCD=180°﹣∠3,
∵∠P+(180°﹣∠1)=∠D+(180°﹣∠3),∠P+∠1=∠B+∠4,
∴2∠P=∠B+∠D,
∴∠P(∠B+∠D)(32°+22°)=27°.
【变式3-1】(2021春 江阴市校级月考)如图1,已知线段AB、CD相交于点O,连接AC、BD,则我们把形如这样的图形称为“8字型”.
(1)求证:∠A+∠C=∠B+∠D;
(2)如图2,若∠CAB和∠BDC的平分线AP和DP相交于点P,与CD、AB分别相交于点M、N.
①以线段AC为边的“8字型”有 个,以点O为交点的“8字型”有 个;
②若∠B=100°,∠C=120°,求∠P的度数;
③若角平分线中角的关系改为“∠CAB=3∠CAP,∠CDB=3∠CDP”,试探究∠P与∠B、∠C之间存在的数量关系,并证明理由.
【解题思路】(1)根据三角形的内角和即可得到结论;
(2)①以线段AC为边的”8字型“有3个,以点O为交点的”8字型“有4个;
②根据角平分线的定义得到∠CAP=∠BAP,∠BDP=∠CDP,再由”8字型“得到∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,两等式相减得到∠C﹣∠P=∠P﹣∠B,即∠P(∠C+∠B),最后把∠C=120°,∠B=100°代入计算即可;
③与②的证明方法一样得到3∠P=∠B+2∠C.
【解答过程】解:(1)证明:在图1中,有∠A+∠C=180°﹣∠AOC,∠B+∠D=180°﹣∠BOD,
∵∠AOC=∠BOD,
∴∠A+∠C=∠B+∠D;
(2)解:①3;4;
故答案为:3,4;
②以M为交点”8字型“中,有∠P+∠CDP=∠C+∠CAP,
以N为交点”8字型“中,有∠P+∠BAP=∠B+∠BDP
∴2∠P+∠BAP+∠CDP=∠B+∠C+∠CAP+∠BDP,
∵AP、DP分别平分∠CAB和∠BDC,
∴∠BAP=∠CAP,∠CDP=∠BDP,
∴2∠P=∠B+∠C,
∵∠B=100°,∠C=120°,
∴∠P(∠B+∠C)(100°+120°)=110°;
③3∠P=∠B+2∠C,其理由是:
∵∠CAB=3∠CAP,∠CDB=3∠CDP,
∴∠BAP∠CAB,∠BDP∠CDB,
以M为交点”8字型“中,有∠P+∠CDP=∠C+∠CAP,
以N为交点”8字型“中,有∠P+∠BAP=∠B+∠BDP
∴∠C﹣∠P=∠CDP﹣∠CAP(∠CDB﹣∠CAB),
∠P﹣∠B=∠BDP﹣∠BAP(∠CDB﹣∠CAB).
∴2(∠C﹣∠P)=∠P﹣∠B.
∴3∠P=∠B+2∠C.
【变式3-2】(2021春 侯马市期末)(1)已知:如图①的图形我们把它称为“8字形”,试说明:∠A+∠B=∠C+∠D.
(2)如图②,AP,CP分别平分∠BAD,∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的度数.
(3)如图(3),直线AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的数量关系是 ;
(4)如图(4),直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的数量关系是 .
【解题思路】(1)根据三角形的内角和等于180°列式整理即可得证;
(2)根据角平分线的定义可得∠1=∠2,∠3=∠4,再根据(1)的结论列出整理即可得解;
(3)表示出∠PAD和∠PCD,再根据(1)的结论列出等式并整理即可得解;
(4)根据四边形的内角和等于360°可得(180°﹣∠1)+∠P+∠4+∠B=360°,∠2+∠P+(180°﹣∠3)+∠D=360°,然后整理即可得解.
【解答过程】解:(1)∵∠A+∠B+∠AOB=180°,∠C+∠D+∠COD=180°,
∴∠A+∠B+∠AOB=∠C+∠D+∠COD.
∵∠AOB=∠COD,
∴∠A+∠B=∠C+∠D.
(2)∵AP,CP分别平分∠BAD,∠BCD,
∴∠BAP=∠PAD,∠BCP=∠PCD,
由(1)的结论得,∠P+∠BCP=∠ABC+∠BAP,①,
∠P+∠PAD=∠ADC+∠PCD②,
①+②得,2∠P+∠BCP+∠PAD=∠BAP+∠PCD+∠ABC+∠ADC,
∴2∠P=∠ABC+∠ADC,
∵∠ABC=36°,∠ADC=16°,
∴∠P=26°.
(3)∵直线AP平分∠BAD,CP平分∠BCD的外角∠BCE,
∴∠PAB=∠PAD,∠PCB=∠PCE,
∴2∠PAB+∠B=180°﹣2∠PCB+∠D,
∴180°﹣2(∠PAB+∠PCB)+∠D=∠B,
∵∠P+∠PAD=∠PCB+∠AOC=∠PCB+∠B+2∠PAD,
∴∠P=∠PAD+∠B+∠PCB=∠PAB+∠B+∠PCB,
∴∠PAB+∠PCB=∠P﹣∠B,
∴180°﹣2(∠P﹣∠B)+∠D=∠B,即∠P=90°(∠B+∠D).
故答案为:∠P=90°(∠B+∠D).
(4)∵直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,
∴∠FAP=∠PAO,∠PCE=∠PCB,
在四边形APCB中,(180°﹣∠FAP)+∠P+∠PCB+∠B=360°①,
在四边形APCD中,∠PAD+∠P+(180°﹣∠PCE)+∠D=360°②,
①+②得:2∠P+∠B+∠D=360°,
∴∠P=180°(∠B+∠D).
故答案为:∠P=180°(∠B+∠D).
【变式3-3】(2021春 高新区校级月考)(1)如图1的图形我们把它称为“8字形”,请说明:∠A+∠B=∠C+∠D.
(2)阅读下面的内容,并解决后面的问题:
(①)如图2,AP、CP分别平分∠BAD、∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的度数.
(②)如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想∠P的度数,并说明理由.
(③)如图4中,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论,无需说明理由.
【解题思路】(1)根据三角形的内角和等于180°列式整理即可得证;
(2)①根据角平分线的定义可得∠1=∠2,∠3=∠4,再根据(1)的结论列出整理即可得解;
②表示出∠PAD和∠PCD,再根据(1)的结论列出等式并整理即可得解;
③根据四边形的内角和等于360°可得(180°﹣∠1)+∠P+∠4+∠B=360°,∠2+∠P+(180°﹣∠3)+∠D=360°,然后整理即可得解.
【解答过程】解:(1)∵∠A+∠B+∠AOB=180°,∠C+∠D+∠COD=180°,
∴∠A+∠B+∠AOB=∠C+∠D+∠COD,
∵∠AOB=∠COD,
∴∠A+∠B=∠C+∠D;
(2)①如图2:∵AP、CP分别平分∠BAD、∠BCD
∴∠1=∠2,∠3=∠4,
由(1)的结论得:∠P+∠3=∠2+∠B①,
∠P+∠1=∠4+∠D②,
①+②,得2∠P+∠1+∠3=∠2+∠4+∠B+∠D,
∵∠ABC=36°,∠ADC=16°,
∴∠P(∠B+∠D)=26°.
②∠P=26°.
如图3:∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,
∴∠1=∠2,∠3=∠4,
由(1)的结论得:∠PAD+∠P=∠PCD+∠D①,∠PAB+∠P=∠PCB+∠B②,
∵∠PAB=∠1,∠1=∠2,
∴∠PAB=∠2,
∴∠2+∠P=∠3+∠B③,
①+③得∠2+∠P+∠PAD+∠P=∠3+∠B+∠PCD+∠D,即2∠P+180°=∠B+∠D+180°,
∴∠P(∠B+∠D )=26°.
③如图4,
∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,
∴∠1=∠2,∠3=∠4,
∴(180°﹣2∠1)+∠B=(180°﹣2∠4)+∠D,
在四边形APCB中,(180°﹣∠1)+∠P+∠4+∠B=360°,
在四边形APCD中,∠2+∠P+(180°﹣∠3)+∠D=360°,
∴2∠P+∠B+∠D=360°,
∴∠P=180°(∠B+∠D).
【题型4 飞镖模型】
【条件】四边形ABDC如上左图所示.
【结论】∠D=∠A+∠B+∠C.(凹四边形凹外角等于三个内角和)
【证明】如上右图,连接AD并延长到E,则:
∠BDC=∠BDE+∠CDE=(∠B+∠1)+(∠2+∠C)=∠B+∠BAC+∠C.本质为两个三角形外角和定理证明.
【例4】(2020春 汝阳县期末)阅读下列材料,然后解答后面的问题.
(1)定义:把四边形的某些边向两方延长,其他各边有不在延长所得直线的同一旁,这样的四边形叫做凹四边形.如图1,四边形ABCD为凹四边形.
(2)性质探究:请完成凹四边形一个性质的证明.
已知:如图2,四边形ABCD是凹四边形.
求证:∠BCD=∠B+∠A+∠D.
(3)性质应用:
如图3,在凹四边形ABCD中,∠BAD的角平分线与∠BCD的角平分线交于点E,若∠ADC=140°,∠AEC=102°,则∠B= °.
【解题思路】(2)延长BC交AD于点M,根据三角形的外角的性质即可解决问题.
(3)利用(2)中结论如图3中,设∠B=x,∠ECB=∠ECD=α,∠EAD=∠EAB=β,列出方程组即可解决问题.
【解答过程】解:(2)延长BC交AD于点M
∵∠BCD是△CDM的外角,
∴∠BCD=∠CMD+∠D,
同理∠CMD是△ABM的外角,
∴∠CMD=∠A+∠B,
∴∠BCD=∠A+∠B+∠D;
(3)如图3中,设∠B=x,∠ECB=∠ECD=α,∠EAD=∠EAB=β.
由(2)可知,,
解得x=64°
故答案为64.
【变式4-1】(2020秋 白银期末)(1)探究:如图1,求证:∠BOC=∠A+∠B+∠C.
(2)应用:如图2,∠ABC=100°,∠DEF=130°,求∠A+∠C+∠D+∠F的度数.
【解题思路】(1)作射线OA,由三角形外角的性质可知∠1+∠B=∠3,∠2+∠C=∠4,两式相加即可得出结论;
(2)连接AD,由(1)的结论可知∠F+∠2+∠3=∠DEF,∠1+∠4+∠C=∠ABC,两式相加即可得出结论.
【解答过程】解:(1)作射线OA,
∵∠3是△ABO的外角,
∴∠1+∠B=∠3,①
∵∠4是△AOC的外角,
∴∠2+∠C=∠4,②
①+②得,∠1+∠B+∠2+∠C=∠3+∠4,
即∠BOC=∠A+∠B+∠C;
(2)连接AD,同(1)可得,∠F+∠2+∠3=∠DEF③,∠1+∠4+∠C=∠ABC④,
③+④得,∠F+∠2+∠3+∠1+∠4+∠C=∠DEF+∠ABC=130°+100°=230°,
即∠A+∠C+∠D+∠F=230°.
【变式4-2】(2020秋 黄石港区校级期中)如图,(1)求证:∠ABC=∠A+∠C+∠ADC;
(2)若∠A=52°,∠C=20°,BE、DE分别平分∠ABC和∠ADC,交于点E,求∠E的度数.
【解题思路】(1)连接DB,延长DB到T.利用三角形的外角的性质证明即可.
(2)利用(1)中结论,以及“8字型”的性质解决问题即可.
【解答过程】(1)证明:连接DB,延长DB到T.
∵∠ABT=∠A+∠ADB,∠CBT=∠C+∠CDB,
∴∠ABC=∠ABT+∠CBT=∠A+∠ADB+∠CDB+∠C=∠A+∠ADC+∠C.
(2)解:设DE交AB于点O.
∵∠ABC=∠A+∠ADC+∠C,BE平分∠ABC,
∴∠OBE∠ABC(∠A+∠ADC+∠C),
∵∠A+∠ADO=∠E+∠OBE,
∴∠E=∠A+∠ADO﹣∠OBE,
∵DE平分∠ADC,
∴∠ADE∠ADC,
∴∠E=∠A∠ADC(∠A+∠ADC+∠C)(∠A﹣∠C)=16°.
【变式4-3】(2020春 福山区期中)直线在同一平面内有平行和相交两种位置关系,线段首尾连接可以变换出很多不同的图形,这些不同的角又有很多不同关系,今天我们就来探究一下这些奇妙的图形吧!
【问题探究】
(1)如图1,请直接写出∠A+∠B+∠C+∠D+∠E= ;
(2)将图1变形为图2,∠A+∠DBE+∠C+∠D+∠E的结果如何?请写出证明过程;
(3)将图1变形为图3,则∠A+∠B+∠C+∠D+∠E的结果如何?请写出证明过程.
【变式拓展】
(4)将图3变形为图4,已知∠BGF=160°,那么∠A+∠B+∠C+∠D+∠E+∠F的度数是 .
【解题思路】(1)根据三角形外角的性质,得到∠2=∠C+∠E,∠1=∠A+∠2,根据三角形内角和等于180°即可求解.
(2)根据三角形外角的性质,得到∠ABE=∠C+∠E,∠DBC=∠A+∠D,即可证明此结论.
(3)根据三角形外角的性质,得到∠DFG=∠B+∠E,∠FGD=∠A+∠C,即可证明此结论;
(4)根据三角形外角的性质,得到∠BGF=∠B+∠2=160°,∠2=∠D+∠F,∠BGF=∠1+∠E=160°,∠1=∠A+∠C,即可得到结论.
【解答过程】(1)解:如图1,∵∠2=∠C+∠E,∠1=∠A+∠2,
∴∠A+∠B+∠C+∠D+∠E=∠1+∠B+∠D=180°,
故答案为:180°;
(2)证明:∵∠ABE=∠C+∠E,∠DBC=∠A+∠D,
∠ABE+∠DBE+∠DBC=180°,
∴∠A+∠DBE+∠C+∠D+∠E=180°
∴将图①变形成图②∠A+∠DBE+∠C+∠D+∠E仍然为180°;
(3)证明:∵在△FGD中,∠DFG+∠FGD+∠D=180°,
∠DFG=∠B+∠E,∠FGD=∠A+∠C,
∴∠A+∠B+∠C+∠D+∠E=180°,
∴将图①变形成图③,则∠A+∠B+∠C+∠D+∠E还为180°;
(4)解:∵∠BGF=∠B+∠2=160°,∠2=∠D+∠F,
∴∠B+∠D+∠F=160°,
∵∠BGF=∠1+∠E=160°,∠1=∠A+∠C,
∴∠A+∠C+∠E=160°,
∴∠A+∠B+∠C+∠D+∠E+∠F=320°,
故答案为:320°.
【题型5 风筝模型】
【条件】四边形ABPC,分别延长AB、AC于点D、E,如上左图所示.
【结论】∠PBD+∠PCE=∠A+∠P.
【证明】如上右图,连接AP,则:∠PBD=∠PAB+∠APB,∠PCE=∠PAC+∠APC,
∴∠PBD+∠PCE=∠PAB+∠APB+∠PAC+∠APC=∠BAC+∠BPC,得证.
【例5】(2020春 灌云县期中)如图,将△ABC的一角折叠,使点C落在△ABC内一点
(1)若∠1=40°,∠2=30°,求∠C的度数;
(2)试通过第(1)问,直接写出∠1、∠2、∠C三者之间的关系.
【解题思路】(1)根据折叠的性质可以得到,∠C′DE=∠CDE,∠C′ED=∠CED,根据平角定义得出∠1+∠C′DC=180°,∠2+∠C′EC=180°,求出∠C′DC+∠C′EC,在四边形C′DCE中,根据内角和定理求出即可;
(2)根据(1)的结果即可得出答案.
【解答过程】解:(1)∵△C′DE是由△CDE折叠而成,
∴∠C=∠C′,∠C′DE=∠CDE,∠C′ED=∠CED,
又∠1+∠C′DC=180°,∠2+∠C′EC=180°,
∴∠C′DC+∠C′EC=360°﹣(∠1+∠2)=290°,
又四边形C′DCE的内角和为360°,
∴∠C′+∠C=70°,
∴∠C=35°.
(2)2∠C=1+∠2,
理由是:∵△C′DE是由△CDE折叠而成,
∴∠C=∠C′,∠C′DE=∠CDE,∠C′ED=∠CED,
又∠1+∠C′DC=180°,∠2+∠C′EC=180°,
∴∠C′DC+∠C′EC=360°﹣(∠1+∠2),
又四边形C′DCE的内角和为360°,
∴∠C′+∠C=360°﹣[360°﹣(∠1+∠2)],
即∠C′+∠C=∠1+∠2,
∵∠C′=∠C
∴2∠C=∠1+∠2.
【变式5-1】(2020秋 路北区期中)如图,在△ABC中,D、E分别是边AB、AC上一点,将△ABC沿DE折叠,使点A落在边BC上.若∠A=55°,求∠1+∠2+∠3+∠4四个角和的度数?
【解题思路】依据三角形内角和定理,可得△ABC中,∠B+∠C=125°,即可得出∠1+∠2+∠3+∠4的度数.
【解答过程】解:∵∠A=55°,
∴△ABC中,∠B+∠C=125°,
又∵∠1+∠2+∠B=180°,∠3+∠4+∠C=180°,
∴∠1+∠2+∠3+∠4=360°﹣(∠B+∠C)=360°﹣125°=235°.
【变式5-2】(2020春 迁安市期末)动手操作:
一个三角形的纸片ABC,沿DE折叠,使点A落在点Aˊ处.
观察猜想
(1)如图1,若∠A=40°,则∠1+∠2= °;
若∠A=55°,则∠1+∠2= °;
若∠A=n°,则∠1+∠2= °.
探索证明:
(2)利用图1,探索∠1、∠2与∠A有怎样的关系?请说明理由.
拓展应用
(3)如图2,把△ABC折叠后,BA′平分∠ABC,CA′平分∠ACB,若∠1+∠2=108°,利用(2)中结论求∠BA′C的度数.
【解题思路】(1)根据翻折变换的性质用∠1、∠2表示出∠ADE和∠AED,再根据三角形的内角和定理列式整理即可得解;根据翻折变换的性质用∠1、∠2表示出∠ADE和∠AED,再根据三角形的内角和定理列式整理即可得解;
(2)由∠BDE、∠CED是△ADE的两个外角知∠BDE=∠A+∠AED、∠CED=∠A+∠ADE,据此得∠BDE+∠CED=∠A+∠AED+∠A+∠ADE,继而可得答案;
(3)由(1)∠1+∠2=2∠A知∠A=54°,根据BA'平分∠ABC,CA'平分∠ACB知∠A'BC+∠A'CB(∠ABC+∠ACB)=90°∠A.利用∠BA'C=180°﹣(∠A'BC+∠A'CB)可得答案.
【解答过程】解:(1)∵点A沿DE折叠落在点A′的位置,
∴∠ADE=∠A′DE,∠AED=∠A′ED,
∴∠ADE(180°﹣∠1),∠AED(180°﹣∠2)
在△ADE中,∠A+∠ADE+∠AED=180°,
∴40°(180°﹣∠1)(180°﹣∠2)=180°,
整理得∠1+∠2=80°;
同理∠A=55°,则∠1+∠2=110°;∠A=n°,则∠1+∠2=2n°;
故答案为:80°;110°;2n°;
(2)∠1+∠2=2∠A,
理由:∵∠BDE、∠CED是△ADE的两个外角,
∴∠BDE=∠A+∠AED,∠CED=∠A+∠ADE,
∴∠BDE+∠CED=∠A+∠AED+∠A+∠ADE,
∴∠1+∠ADE+∠2+∠AED=2∠A+∠AED+∠ADE,
即∠1+∠2=2∠A;
(3)由(1)∠1+∠2=2∠A,得2∠A=108°,
∴∠A=54°,
∵BA'平分∠ABC,CA'平分∠ACB,
∴∠A'BC+∠A'CB(∠ABC+∠ACB)
(180°﹣∠A)
=90°∠A.
∴∠BA'C=180°﹣(∠A'BC+∠A'CB),
=180°﹣(90°∠A)
=90°∠A
=90°54°
=117°.
【变式5-3】(2021春 高邮市校级期末)直角△ABC中,∠C=90°,点D,E分别是边AC,BC上的点,点P是一动点,令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在线段AB上,如图1所示,且∠α=50°,则∠1+∠2= ;
(2)若点P在边AB上运动,如图2所示,则∠α、∠1、∠2之间有何关系,并说明理由;
(3)如图3,若点P在斜边BA的延长线上运动(CE<CD),请写出∠α、∠1、∠2之间的关系式.
【解题思路】(1)根据四边形内角和定理以及邻补角的定义得出∠1+∠2=∠C+∠α,进而得出即可;
(2)利用(1)中所求得出答案即可;
(3)利用三角外角的性质分三种情况讨论即可.
【解答过程】解:(1)∵∠1+∠2+∠CDP+∠CEP=360°,∠C+∠α+∠CDP+∠CEP=360°,
∴∠1+∠2=∠C+∠α,
∵∠C=90°,∠α=50°,
∴∠1+∠2=140°;
(2)由(1)得出:
∠α+∠C=∠1+∠2,
∴∠1+∠2=90°+α.
(3)如图,
分三种情况:在BA延长线上取点P,连接EP、DP,
如图1,由三角形的外角性质,∠2=∠C+∠1+∠α,
∴∠2﹣∠1=90°+∠α;
如图2,∠α=0°,∠2=∠1+90°;
如图3,∠2=∠1﹣∠α+∠C,
∴∠1﹣∠2=∠α﹣90°.
【题型6 两内角角平分线模型】
【条件】△ABC中,BI、CI分别是∠ABC和∠ACB的角平分线,且相交于点I.
【结论】
【证明】∵BI是∠ABC平分线,∴∵CI是∠ACB平分线,∴
由A→B→I→C→A的飞镖模型可知:
∠I=∠A+∠2+∠3=∠A++=∠A+=.
【例6】(2020春 兴化市月考)如图,△ABC的角平分线BD、CE相交于点P.
(1)若∠ABC=50°,∠ACB=70°,则∠A= °;
(2)若∠A=80°,试求∠BPC的度数;
(3)试直接写出∠DPC与∠A之间的数量关系:∠DPC= .
【解题思路】先根据角平分线的定义得到∠1∠ABC,∠2∠ACB,再根据三角形内角和定理得∠BPC=180°﹣∠1﹣∠2=180°(∠ABC+∠ACB),加上∠ABC+∠ACB=180°﹣∠A,易得∠BPC=90°∠A,然后根据此结论解决各小题.
【解答过程】解:∵∠ABC,∠ACB的平分线相交于点P,
∴∠1∠ABC,∠2∠ACB,
∴∠BPC=180°﹣∠1﹣∠2=180°∠ABC∠ACB=180°(∠ABC+∠ACB),
∵∠ABC+∠ACB=180°﹣∠A,
∴∠BPC=180°(180°﹣∠A)=90°∠A,
(1)∵∠ABC=50°,∠ACB=70°,
∴∠A=180°﹣50°﹣70°=60°.
故答案为60.
(2)∵∠A=80°,
∴∠BPC=90°80°=130°;
(3)∵∠BPC=90°∠A,
∴∠DPC=180°﹣(90°∠A)=90°∠A.
故答案为:90°∠A.
【变式6-1】(2020秋 硚口区期中)如图,在Rt△ABC中,∠C=90°,BD平分∠ABC交AC于点D,AP平分∠BAC交BD于点P,∠BDC=58°,求∠BAP的度数.
【解题思路】先利用三角形内角和定理的推论,得出∠DBC=32°,再由角平分线的定义得到∠ABD=∠DBC=32°,求出∠ABC,再求出∠CAB即可解决问题.
【解答过程】解:∵∠BDC=58°,∠C=90°,
∴∠DBC=90°﹣∠BDC=32°,
∵BD平分∠ABC,
∴∠ABD=∠DBC=32°,
∴∠ABC=2∠ABD=64°,
∴∠CAB=90°﹣∠ABC=26°,
∵PA平分∠BAC,
∴∠BAP∠CAB=13°.
【变式6-2】(2020春 浦东新区期末)如图,点A、B分别在射线ON、OM上运动(不与点O重合),AC、BC分别是∠BAO和∠ABO的角平分线,BC延长线交ON于点G.
(1)若∠MON=60°,则∠ACB= °;若∠MON=90°,则∠ACB= °;
(2)若∠MON=n°.请求出∠ACG的度数;(用含n的代数式表示)
【解题思路】(1)由三角形内角和定理和角平分线的定义即可得到结论;
(2)由三角形内角和定理和角平分线的定义即可得到结论.
【解答过程】解:(1)∵∠MON=60°,
∴∠OBA+∠OAB=120°,
∵∠OBA、∠OAB的平分线交于点C,
∴∠ABC+∠BAC120°=60°,
∴∠ACB=180°﹣60°=120°,
∵∠MON=90°,
∴∠OBA+∠OAB=90°,
∵∠OBA、∠OAB的平分线交于点C,
∴∠ABC+∠BAC90°=45°,
∴∠ACB=180°﹣45°=135°;
(2)在△AOB中,∠OBA+∠OAB=180°﹣∠AOB=180°﹣n°,
∵∠OBA、∠OAB的平分线交于点C,
∴∠ABC+∠BAC(∠OBA+∠OAB)(180°﹣n°),
即∠ABC+∠BAC=90°n°,
∴∠ACB=180°﹣(∠ABC+∠BAC)=180°﹣(90°n°)=90°n°,
∴∠ACG=180°﹣(90°n°)=90°n°.
故答案为:120,135.
【变式6-3】(2020春 南岗区期末)已知在△ABC中,∠A=100°,点D在△ABC的内部连接BD,CD,且∠ABD=∠CBD,∠ACD=∠BCD.
(1)如图1,求∠BDC的度数;
(2)如图2,延长BD交AC于点E,延长CD交AB于点F,若∠AED﹣∠AFD=12°,求∠ACF的度数.
【解题思路】(1)依据三角形内角和定理以及角平分线的定义,即可得到∠BDC的度数;
(2)设∠ACF=α,则∠BCD=α,∠CBD=40°﹣α=∠ABD,依据三角形外角性质,即可得到∠AED=∠ACF+∠CDF,∠AFD=∠ABE+∠BDF,再根据∠AED﹣∠AFD=12°,即可得到α的值.
【解答过程】解:(1)∵∠A=100°,
∴∠ABC+∠ACB=80°,
又∵∠ABD=∠CBD,∠ACD=∠BCD,
∴∠CBD∠ABC,∠BCD∠ACB,
∴∠CBD+∠BCD(∠ABC+∠ACB)=40°,
∴∠BDC=180°﹣40°=140°;
(2)设∠ACF=α,则∠BCD=α,
∵∠BDC=140°,
∴∠CBD=40°﹣α=∠ABD,
∵∠AED是△DCE的外角,∠AFD是△BDF的外角,
∴∠AED=∠ACF+∠CDF,∠AFD=∠ABE+∠BDF,
∴∠AED﹣∠AFD=∠ACF+∠CDF﹣∠ABE﹣∠BDE=α﹣(40°﹣α)=12°,
解得α=26°,
∴∠ACF=26°.
【题型7 两外角角平分线模型】
【条件】△ABC中,BI、CI分别是△ABC的外角的角平分线,且相交于点O.
【结论】.
【证明】∵BO是∠EBC平分线,∴,∵CO是∠FCB平分线,∴
由△BCO中内角和定理可知:∠O=180°-∠2 -∠5 =180°--=180°--===.
【例7】(2020春 浦东新区期末)已知:如图,△ABC的两个外角的平分线交于点P,如果∠A=40°,求∠BPC的度数.
【解题思路】根据三角形内角和定理得到∠ABC+∠ACB=140°,根据角平分线的定义、三角形内角和定理计算即可.
【解答过程】解:∵∠A=40°,
∴∠ABC+∠ACB=180°﹣40°=140°,
∴∠EBC+∠FCB=360°﹣140°=220°,
∵BP、CP是△ABC的外角平分线,
∴∠PBC∠EBC,∠PCB∠FCB,
∴∠PBC+∠PCB(∠EBC+∠FCB)=110°,
∴∠BPC=180°﹣(∠PBC+∠PCB)=70°.
【变式7-1】(2020秋 鄂伦春自治旗月考)如图,△ABC中,分别延长△ABC的边AB、AC到D、E,∠CBD与∠BCE的平分线相交于点P,爱动脑筋的小明在写作业的时发现如下规律:
(1)若∠A=60°,则∠P= °;
(2)若∠A=40°,则∠P= °;
(3)若∠A=100°,则∠P= °;
(4)请你用数学表达式归纳∠A与∠P的关系 .
【解题思路】(1)若∠A=60°,则有∠ABC+∠ACB=120°,∠DBC+∠BCE=360°﹣120°=240°,根据角平分线的定义可以求得∠PBC+∠PCB的度数,再利用三角形的内角和定理即可求得∠P的度数.
(2)(3)和(1)的解题步骤相似.
(4)利用角平分线的性质和三角形的外角性质可求出∠BCP(∠A+∠ABC),∠CBP(∠A+∠ACB);再利用三角形内角和定理便可求出∠A与∠P的关系.
【解答过程】解:(1)∵∠A=60°,
∴∠ABC+∠ACB=180°﹣60°=120°,∠DBC+∠BCE=360°﹣120°=240°,
又∵∠CBD与∠BCE的平分线相交于点P,
∴∠PBC∠DBC,∠PCB∠BCE,
∴∠PBC+∠PCB(∠DBC+∠ECB)=120°,
∴∠P=60°.
同理得:(2)70°;
(3)40°
(4)∠P=90°∠A.理由如下:
∵BP平分∠DBC,CP平分∠BCE,
∴∠DBC=2∠CBP,∠BCE=2∠BCP
又∵∠DBC=∠A+∠ACB∠BCE=∠A+∠ABC,
∴2∠CBP=∠A+∠ACB,2∠BCP=∠A+∠ABC,
∴2∠CBP+2∠BCP=∠A+∠ACB+∠A+∠ABC=180°+∠A,
∴∠CBP+∠BCP=90°∠A
又∵∠CBP+∠BCP+∠P=180°,
∴∠P=90°∠A.
故答案为:60,70,40,90°∠A.
【变式7-2】(2020春 石城县期末)如图,在四边形ABCD中,AD∥BC,∠B=∠D,延长BA至点E,连接CE,且CE交AD于点F,∠EAD和∠ECD的角平分线相交于点P.
(1)①直接写出AB和CD的位置关系: ;
②求证:∠EAD∠ECD=∠APC.
(2)若∠B=70°,∠E=60°,求∠APC的度数;
(3)若∠APC=m°,∠EFD=n°,请你探究m和n之间的数量关系.
【解题思路】(1)①根据平行线的性质与判定解答即可;②过点P作PQ∥AB,则∠EAP=∠APQ,再根据平行线的性质证明即可;
(2)由AD∥BC,AB∥CD,可得∠EAD=∠B=70°,∠ECD=∠E=60°,再根据角平分线的性质解答即可;
(3)过点F作FH∥AB,根据平行线的性质以及角的和差关系解答即可.
【解答过程】解:(1)①∵AD∥BC,
∴∠EAD=∠B,
∵∠B=∠D,
∴∠EAD=∠D,
∴AB∥CD;
故答案为:AB∥CD;
②证明:过点P作PQ∥AB,则∠EAP=∠APQ,
∵AB∥CD,
∴PQ∥CD,
∴∠DCP=∠CPQ,
∵AB∥CD,
∴PQ∥CD,
∴∠DCP=∠CPQ,
∵∠EAP∠EAD,∠DCP∠ECD,
∴∠EAD∠ECD=∠APC.
(2)由(1)知AD∥BC,AB∥CD,
∴∠EAD=∠B=70°,∠ECD=∠E=60°,
由(1)知∠EAD+∠ECD=2∠APC,
∴∠APC(70°+60°)=65°;
(3)过点F作FH∥AB,则∠EAD=∠AFH,
∵AB∥CD,
∴FH∥CD,
∴∠ECD=∠CFH,
∴∠EAD+∠ECD=∠AFH+∠CFH=∠AFC=∠EFD,
由(1)知∠EAD+∠ECD=2∠APC,
∴∠EFD=2∠APC,
∵∠APC=m°,∠EFD=n°,
∴mn.
【变式7-3】(2021春 东坡区校级期末)如图,四边形ABCD,BE、DF分别平分四边形的外角∠MBC和∠NDC,若∠BAD=α,∠BCD=β.
(1)如图1,若α+β=120°,求∠MBC+∠NDC的度数;
(2)如图1,若BE与DF相交于点G,∠BGD=30°,请写出α、β所满足的等量关系式;
(3)如图2,若α=β,判断BE、DF的位置关系,并说明理由.
【解题思路】(1)∠ABC+∠ADC=360°﹣(α+β)=240°,则∠MBC+∠NDC=180°﹣∠ABC+180°﹣∠ADC=α+β=120°.
(2)连接BD,由(1)有,∠MBC+∠NDC=α+β,BE、DF分别平分四边形的外角∠MBC和∠NDC,则∠CBG+∠CDG∠MBC∠NDC(∠MBC+∠NDC)(α+β),在△BCD中,∠BDC+∠CBD=180°﹣∠BCD=180°﹣β,在△BDG中,∠GBD+∠GDB+∠BGD=180°,(∠CBG+∠CDG)+(∠BDC+∠CBD)+∠BGD=180°,则(α+β)+180°﹣β+30°=180°,即β﹣α=60°,
(3)由(1)有,∠MBC+∠NDC=α+β,BE、DF分别平分四边形的外角∠MBC和∠NDC,则∠CBE+∠CDH(α+β),∠CBE+β﹣∠DHB(α+β),根据α=β,则有∠CBE+β﹣∠DHB(β+β)=β,∠CBE=∠DHB,则BE∥DF.
【解答过程】解:(1)∵∠ABC+∠ADC=360°﹣(α+β)=240°,
∴∠MBC+∠NDC=180°﹣∠ABC+180°﹣∠ADC=α+β=120°.
(2)β﹣α=60°
理由:如图1,连接BD,
由(1)有,∠MBC+∠NDC=α+β,
∵BE、DF分别平分四边形的外角∠MBC和∠NDC,
∴∠CBG∠MBC,∠CDG∠NDC,
∴∠CBG+∠CDG∠MBC∠NDC(∠MBC+∠NDC)(α+β),
在△BCD中,∠BDC+∠CBD=180°﹣∠BCD=180°﹣β,
在△BDG中,∠GBD+∠GDB+∠BGD=180°,
∴∠CBG+∠CBD+∠CDG+∠BDC+∠BGD=180°,
∴(∠CBG+∠CDG)+(∠BDC+∠CBD)+∠BGD=180°,
∴(α+β)+180°﹣β+30°=180°,
∴β﹣α=60°,
(3)平行,
理由:如图2,延长BC交DF于H,
由(1)有,∠MBC+∠NDC=α+β,
∵BE、DF分别平分四边形的外角∠MBC和∠NDC,
∴∠CBE∠MBC,∠CDH∠NDC,
∴∠CBE+∠CDH∠MBC∠NDC(∠MBC+∠NDC)(α+β),
∵∠BCD=∠CDH+∠DHB,
∴∠CDH=∠BCD﹣∠DHB=β﹣∠DHB,
∴∠CBE+β﹣∠DHB(α+β),
∵α=β,
∴∠CBE+β﹣∠DHB(β+β)=β,
∴∠CBE=∠DHB,
∴BE∥DF.
【题型8 内外角角平分线模型】
【条件】△ABC中,BP、CP分别是△ABC的内角和外角的角平分线,且相交于点P.
【结论】
【证明】 ∵BP是∠ABC平分线,∴ ∵CP是∠ACE平分线,∴
由△ABC外角定理可知:∠ACE=∠ABC+∠A即:2∠1=2∠3+∠A ……①
对①式两边同时除以2,得:∠1=∠3+ ……②又在△BPC中由外角定理可知:∠1=∠3+∠P ……③
比较②③式子可知:.==.
【例8】(2021春 靖江市校级月考)如图①,△ABC中,BD平分∠ABC,且与△ABC的外角∠ACE的角平分线交于点D.
(1)若∠ABC=70°,∠ACB=40°,求∠D的度数;
(2)若把∠A截去,得到四边形MNCB,如图②,猜想∠D、∠M、∠N的关系,并说明理由.
【解题思路】(1)根据三角形内角和定理以及角平分线性质,先求出∠D、∠A的等式,推出∠A=2∠D,最后代入求出即可;
(2)根据(1)中的结论即可得到结论.
【解答过程】解:(1)∵∠ACE=∠A+∠ABC,
∴∠ACD+∠DCE=∠A+∠ABD+∠DBC,∠DCE=∠D+∠DBC,
又BD平分∠ABC,CD平分∠ACE,
∴∠ABD=∠DBE,∠ACD=∠ECD,
∴∠A=2(∠DCE﹣∠DBC),∠D=∠DCE﹣∠DBC,
∴∠A=2∠D,
∵∠ABC=70°,∠ACB=40°,
∴∠A=180°﹣∠ABC﹣∠ACB=70°,
∴∠D=35°;
(2)∠D(∠M+∠N﹣180°);
理由:延长BM、CN交于点A,
∵∠A+∠ANM+∠AMN=180°,∠AMN+∠BMN=180°,∠ANM+∠CNM=180°,
∴∠A=180°﹣∠ANM﹣∠AMN=180°﹣(180°﹣∠CNM)﹣(180°﹣∠BMN)=180°﹣180°+∠CNM﹣180°+∠BMN,
则∠A=∠BMN+∠CNM﹣180°,
由(1)知,∠D∠A,
∴∠D(∠BMN+∠CNM﹣180°).
【变式8-1】(2020春 兴化市期中)(1)思考探究:如图,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,已知∠ABC=70°,∠ACD=100°.求∠A和∠P的度数;
(2)类比探究:如图,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,已知∠P=n°.求∠A的度数(用含n的式子表示);
(3)拓展迁移:已知,在四边形ABCD中,四边形ABCD的内角∠ABC与外角∠DCE的平分线所在直线相交于点P,∠P=n°,请画出图形;并探究出∠A+∠D的度数(用含n的式子表示).
【解题思路】(1)根据三角形外角的性质可求∠A,根据角平分线的定义和三角形外角的性质可求∠P;
(2)根据三角形的一个外角等于与它不相邻的两个内角的和可得∠PCD=∠P+∠PBC,∠ACD=∠A+∠ABC,再根据角平分线的性质即可得解;
(3)添加辅助线,利用(2)中结论解决问题即可.
【解答过程】解:(1)∵∠ABC=70°,∠ACD=100°,
∴∠A=100°﹣70°=30°,
∵P点是∠ABC和外角∠ACD的角平分线的交点,
∴∠PCD∠ACD=50°,∠PBC∠ABC=35°,
∴∠P=50°﹣35°=15°;
(2)∠A=2n°.
理由:∵∠PCD=∠P+∠PBC,∠ACD=∠A+∠ABC,
∵P点是∠ABC和外角∠ACD的角平分线的交点,
∴∠ACD=2∠PCD,∠ABC=2∠PBC,
∴∠A+∠ABC=2(∠P+∠PBC),
∠A+∠ABC=2∠P+2∠PBC,
∠A+∠ABC=2∠P+∠ABC,
∴∠A=2∠P,
∴∠A=2n°;
(3)(Ⅰ)如图②延长BA交CD的延长线于F.
∵∠F=180°﹣∠FAD﹣∠FDA=180°﹣(180°﹣∠A)﹣(180°﹣∠D)=∠A+∠D﹣180°,
由(2)可知:∠F=2∠P=2n°,
∴∠A+∠D=180°+2n°.
(Ⅱ)如图③,延长AB交DC的延长线于F.
∵∠F=180°﹣∠A﹣∠D,∠P∠F,
∴∠P(180°﹣∠A﹣∠D)=90°(∠A+∠D).
∴∠A+∠D=180°﹣2n°
综上所述:∠A+∠D=180°+2n°或180°﹣2n°.
【变式8-2】(2020秋 平舆县期中)已知:如图,∠MON=90°,点A、B分别在射线OM、ON上移动(不与点O重合),AC平分∠MAB,AC的反向延长线与∠ABO的平分线相交于点D.
(1)当∠ABO=70°时、∠D的度数是多少?
(2)随着点A、B的移动,试问∠D的大小是否变化?请说出你的理由.
【解题思路】(1)利用三角形的外角性质可求出∠MAB的度数,由AC平分∠MAB,BD平分∠ABO,利用角平分线的定义可求出∠CAB和∠ABD的度数,再利用三角形的外角性质可求出∠D的度数;
(2)利用三角形的外角性质及角平分线的定义可用∠ABO表示出∠CAB和∠ABD的度数,再利用三角形的外角性质可求出∠D的度数为固定值,进而可得出∠D的大小不发生变化.
【解答过程】解:(1)∵∠MON=90°,∠ABO=70°,
∴∠MAB=∠AOB+∠ABO=90°+70°=160°.
∵AC平分∠MAB,
∴∠CAB∠MAB=80°.
∵BD平分∠ABO,
∴∠ABD∠ABO=35°.
又∵∠CAB=∠ABD+∠D,
∴∠D=∠CAB﹣∠ABD=80°﹣35°=45°.
(2)∠D的大小不变,理由如下:
∵∠MAB=∠AOB+∠ABO=90°+∠ABO,AC平分∠MAB,
∴∠CAB∠MAB=45°∠ABO.
∵BD平分∠ABO,
∴∠ABD∠ABO.
又∵∠CAB=∠ABD+∠D,
∴∠D=∠CAB﹣∠ABD=45°∠ABO∠ABO=45°,
∴∠D的大小不发生变化.
【变式8-3】(2020春 惠安县期末)在△ABC中,∠ACB的平分线CD与外角∠EAC的平分线AF所在的直线交于点D.
(1)如图1,若∠B=60°,求∠D的度数;
(2)如图2,把△ACD沿AC翻折,点D落在D′处.
①当AD′⊥AD时,求∠BAC的度数;
②试确定∠DAD′与∠BAC的数量关系,并说明理由.
【解题思路】(1)利用角平分线的定义和三角形的外角的性质进行代换可以得出∠B=2∠D,已知∠B=60°,可求∠D的度数;
(2)①根据折叠,可得等角,再利用特殊角,和周角的意义可以计算出∠DAC的度数,再利用平角的意义,可求出∠CAF,进而得出∠BAC的度数;
②设∠DAD′为任意角度,通过折叠、外角、角平分线,平角等代换,得出∠DAD′与∠BAC的数量关系,即∠DAD′与∠BAC互补的结论.
【解答过程】解:(1)如图1,
∵CD平分∠ACB,
∴∠ACD=∠DCB∠ACB,
∵AF是外角∠EAC的平分线,
∴∠CAF=∠FAE∠CAE,
又∵∠CAF=∠D+∠ACD,
∠CAE=∠B+∠ACB,
∴∠D∠B=30°;
(2)如图2,由折叠得:∠DAC=∠D′AC,
①当AD′⊥AD时,即:∠DAD′=90°,
∴∠DAC=∠D′AC=135°,
∴∠CAF=180°﹣135°=45°=∠FAE,
∴∠BAC=180°﹣45°﹣45°=90°,
答:当AD′⊥AD时,∠BAC=90°.
②设∠DAD′=α,则∠DAC=∠D′AC(360°﹣α)=180°α,
∴∠CAF=180°﹣∠DAC=180°﹣(180°α)α,
∴∠CAE=2∠CAF=α,
∴∠BAC=180°﹣α,
即:∠BAC+∠DAD′=180°,
答:∠DAD′与∠BAC的数量关系是:∠BAC+∠DAD′=180°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
角度计算中的经典模型8大题型
【题型1 双垂直模型】
【条件】∠B=∠D=∠ACE=90°.
【结论】∠BAC=∠DCE,∠ACB=∠CED.
【证明】∵∠B=∠D=∠ACE=90°;∴∠BAC+∠ACB=90°;又∠ECD+∠ACB=90°;∴∠BAC=∠DCE
同理,∠ACB+∠DCE =90°,且∠CED+∠DCE =90°;∴∠ACB=∠CED,得证.
【例1】(2020秋 铁西区期中)(1)如图①,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,求证:∠ACD=∠B;
(2)如图②,在Rt△ABC中,∠C=90°,D、E分别在AC,AB上,且∠ADE=∠B,判断△ADE的形状?并说明理由?
(3)如图③,在Rt△ABC和Rt△DBE中,∠C=90°,∠E=90°,点C,B,E在同一直线上,若AB⊥BD,AB=BD,则CE与AC,DE有什么等量关系,并证明.
【变式1-1】(2021春 盐城期末)已知:如图,在△ABC中,∠ACB=90°,CE⊥AB,F为边BC上一点,连接AF交CE于点G,∠CGF=∠CFG.求证:AF平分∠BAC.
【变式1-2】(2020秋 丰城市期中)(1)如图①,△ABC是锐角三角形,高BD,CE相交于点H,找出∠BHC和∠A之间存在何种等量关系;并证明你的结论
(2)如图②,若△ABC是钝角三角形,∠A>90°,高BD,CE所在的直线相交于点H,请你判断此时(1)中的等量关系是否仍然成立?并说明理由.
【变式1-3】(2021春 庐江县期末)如图1,AB⊥BC于点B,CD⊥BC于点C,点E在线段BC上,且AE⊥DE.
(1)求证:∠EAB=∠CED;
(2)如图2,AF、DF分别平分∠BAE和∠CDE,则∠F的度数是 (直接写出答案即可);
(3)如图3,EH平分∠CED,EH的反向延长线交∠BAE的平分线AF于点G.求证:EG⊥AF.(提示:三角形内角和等于180°)
【题型2 A字模型】
【条件】△ADE与△ABC.
【结论】∠AED+∠ADE=∠B+C.
【证明】根据三角形内角和可得,∠AED+∠ADE=180°-∠A,∠B+C=180°-∠A,
∴∠AED+∠ADE=∠B+C,得证.
【例2】(2021春 资中县月考)如图所示,△ABC中,∠C=75°,若沿图中虚线截去∠C,则∠1+∠2等于多少度?
【变式2-1】(2020春 长沙县校级期中)如图,已知∠A=40°,求∠1+∠2+∠3+∠4的度数.
【变式2-2】(2020春 常州期中)如图,△ABC中,∠B=68°,∠A比∠C大28°,点D、E分别在AB、BC上.连接DE,∠DEB=42°.
(1)求∠A的度数;
(2)判断DE与AC之间的位置关系,并说明理由.
【变式2-3】(2020春 新野县期末)旧知新意:
我们容易证明,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?
尝试探究:
(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?
初步应用:
(2)如图2,在△ABC纸片中剪去△CDE,得到四边形ABDE,∠1=130°,则∠2﹣∠C= ;
(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请利用上面的结论直接写出答案 .
【题型3 8字模型】
【条件】AD、BC相交于点O.
【结论】∠A+∠B=∠C+∠D.(上面两角之和等于下面两角之和)
【证明】在△ABO中,由内角和定理:∠A+∠B+∠BOA=180°,在△CDO中,∠C+∠D+∠COD=180°,
∴∠A+∠B+∠BOA=180°=∠C+∠D+∠COD,由对顶角相等:∠BOA=∠COD
∴∠A+∠B=∠C+∠D,得证.
【例3】(2020秋 庆阳期中)【问题背景】(1)如图1的图形我们把它称为“8字形”,请说明∠A+∠B=∠C+∠D;
【问题探究】
(2)如图2,直线AP平分△BAO的外角∠FAD,CP平分△OCD的外角∠BCE,若∠ABC=32°,∠ADC=22°,求∠P的度数.
【变式3-1】(2021春 江阴市校级月考)如图1,已知线段AB、CD相交于点O,连接AC、BD,则我们把形如这样的图形称为“8字型”.
(1)求证:∠A+∠C=∠B+∠D;
(2)如图2,若∠CAB和∠BDC的平分线AP和DP相交于点P,与CD、AB分别相交于点M、N.
①以线段AC为边的“8字型”有 个,以点O为交点的“8字型”有 个;
②若∠B=100°,∠C=120°,求∠P的度数;
③若角平分线中角的关系改为“∠CAB=3∠CAP,∠CDB=3∠CDP”,试探究∠P与∠B、∠C之间存在的数量关系,并证明理由.
【变式3-2】(2021春 侯马市期末)(1)已知:如图①的图形我们把它称为“8字形”,试说明:∠A+∠B=∠C+∠D.
(2)如图②,AP,CP分别平分∠BAD,∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的度数.
(3)如图(3),直线AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的数量关系是 ;
(4)如图(4),直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的数量关系是 .
【变式3-3】(2021春 高新区校级月考)(1)如图1的图形我们把它称为“8字形”,请说明:∠A+∠B=∠C+∠D.
(2)阅读下面的内容,并解决后面的问题:
(①)如图2,AP、CP分别平分∠BAD、∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的度数.
(②)如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想∠P的度数,并说明理由.
(③)如图4中,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论,无需说明理由.
【题型4 飞镖模型】
【条件】四边形ABDC如上左图所示.
【结论】∠D=∠A+∠B+∠C.(凹四边形凹外角等于三个内角和)
【证明】如上右图,连接AD并延长到E,则:
∠BDC=∠BDE+∠CDE=(∠B+∠1)+(∠2+∠C)=∠B+∠BAC+∠C.本质为两个三角形外角和定理证明.
【例4】(2020春 汝阳县期末)阅读下列材料,然后解答后面的问题.
(1)定义:把四边形的某些边向两方延长,其他各边有不在延长所得直线的同一旁,这样的四边形叫做凹四边形.如图1,四边形ABCD为凹四边形.
(2)性质探究:请完成凹四边形一个性质的证明.
已知:如图2,四边形ABCD是凹四边形.
求证:∠BCD=∠B+∠A+∠D.
(3)性质应用:
如图3,在凹四边形ABCD中,∠BAD的角平分线与∠BCD的角平分线交于点E,若∠ADC=140°,∠AEC=102°,则∠B= °.
【变式4-1】(2020秋 白银期末)(1)探究:如图1,求证:∠BOC=∠A+∠B+∠C.
(2)应用:如图2,∠ABC=100°,∠DEF=130°,求∠A+∠C+∠D+∠F的度数.
【变式4-2】(2020秋 黄石港区校级期中)如图,(1)求证:∠ABC=∠A+∠C+∠ADC;
(2)若∠A=52°,∠C=20°,BE、DE分别平分∠ABC和∠ADC,交于点E,求∠E的度数.
【变式4-3】(2020春 福山区期中)直线在同一平面内有平行和相交两种位置关系,线段首尾连接可以变换出很多不同的图形,这些不同的角又有很多不同关系,今天我们就来探究一下这些奇妙的图形吧!
【问题探究】
(1)如图1,请直接写出∠A+∠B+∠C+∠D+∠E= ;
(2)将图1变形为图2,∠A+∠DBE+∠C+∠D+∠E的结果如何?请写出证明过程;
(3)将图1变形为图3,则∠A+∠B+∠C+∠D+∠E的结果如何?请写出证明过程.
【变式拓展】
(4)将图3变形为图4,已知∠BGF=160°,那么∠A+∠B+∠C+∠D+∠E+∠F的度数是 .
【题型5 风筝模型】
【条件】四边形ABPC,分别延长AB、AC于点D、E,如上左图所示.
【结论】∠PBD+∠PCE=∠A+∠P.
【证明】如上右图,连接AP,则:∠PBD=∠PAB+∠APB,∠PCE=∠PAC+∠APC,
∴∠PBD+∠PCE=∠PAB+∠APB+∠PAC+∠APC=∠BAC+∠BPC,得证.
【例5】(2020春 灌云县期中)如图,将△ABC的一角折叠,使点C落在△ABC内一点
(1)若∠1=40°,∠2=30°,求∠C的度数;
(2)试通过第(1)问,直接写出∠1、∠2、∠C三者之间的关系.
【变式5-1】(2020秋 路北区期中)如图,在△ABC中,D、E分别是边AB、AC上一点,将△ABC沿DE折叠,使点A落在边BC上.若∠A=55°,求∠1+∠2+∠3+∠4四个角和的度数?
【变式5-2】(2020春 迁安市期末)动手操作:
一个三角形的纸片ABC,沿DE折叠,使点A落在点Aˊ处.
观察猜想
(1)如图1,若∠A=40°,则∠1+∠2= °;
若∠A=55°,则∠1+∠2= °;
若∠A=n°,则∠1+∠2= °.
探索证明:
(2)利用图1,探索∠1、∠2与∠A有怎样的关系?请说明理由.
拓展应用
(3)如图2,把△ABC折叠后,BA′平分∠ABC,CA′平分∠ACB,若∠1+∠2=108°,利用(2)中结论求∠BA′C的度数.
【变式5-3】(2021春 高邮市校级期末)直角△ABC中,∠C=90°,点D,E分别是边AC,BC上的点,点P是一动点,令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在线段AB上,如图1所示,且∠α=50°,则∠1+∠2= ;
(2)若点P在边AB上运动,如图2所示,则∠α、∠1、∠2之间有何关系,并说明理由;
(3)如图3,若点P在斜边BA的延长线上运动(CE<CD),请写出∠α、∠1、∠2之间的关系式.
【题型6 两内角角平分线模型】
【条件】△ABC中,BI、CI分别是∠ABC和∠ACB的角平分线,且相交于点I.
【结论】
【证明】∵BI是∠ABC平分线,∴∵CI是∠ACB平分线,∴
由A→B→I→C→A的飞镖模型可知:
∠I=∠A+∠2+∠3=∠A++=∠A+=.
【例6】(2020春 兴化市月考)如图,△ABC的角平分线BD、CE相交于点P.
(1)若∠ABC=50°,∠ACB=70°,则∠A= °;
(2)若∠A=80°,试求∠BPC的度数;
(3)试直接写出∠DPC与∠A之间的数量关系:∠DPC= .
【变式6-1】(2020秋 硚口区期中)如图,在Rt△ABC中,∠C=90°,BD平分∠ABC交AC于点D,AP平分∠BAC交BD于点P,∠BDC=58°,求∠BAP的度数.
【变式6-2】(2020春 浦东新区期末)如图,点A、B分别在射线ON、OM上运动(不与点O重合),AC、BC分别是∠BAO和∠ABO的角平分线,BC延长线交ON于点G.
(1)若∠MON=60°,则∠ACB= °;若∠MON=90°,则∠ACB= °;
(2)若∠MON=n°.请求出∠ACG的度数;(用含n的代数式表示)
【变式6-3】(2020春 南岗区期末)已知在△ABC中,∠A=100°,点D在△ABC的内部连接BD,CD,且∠ABD=∠CBD,∠ACD=∠BCD.
(1)如图1,求∠BDC的度数;
(2)如图2,延长BD交AC于点E,延长CD交AB于点F,若∠AED﹣∠AFD=12°,求∠ACF的度数.
【题型7 两外角角平分线模型】
【条件】△ABC中,BI、CI分别是△ABC的外角的角平分线,且相交于点O.
【结论】.
【证明】∵BO是∠EBC平分线,∴,∵CO是∠FCB平分线,∴
由△BCO中内角和定理可知:∠O=180°-∠2 -∠5 =180°--=180°--===.
【例7】(2020春 浦东新区期末)已知:如图,△ABC的两个外角的平分线交于点P,如果∠A=40°,求∠BPC的度数.
【变式7-1】(2020秋 鄂伦春自治旗月考)如图,△ABC中,分别延长△ABC的边AB、AC到D、E,∠CBD与∠BCE的平分线相交于点P,爱动脑筋的小明在写作业的时发现如下规律:
(1)若∠A=60°,则∠P= °;
(2)若∠A=40°,则∠P= °;
(3)若∠A=100°,则∠P= °;
(4)请你用数学表达式归纳∠A与∠P的关系 .
【变式7-2】(2020春 石城县期末)如图,在四边形ABCD中,AD∥BC,∠B=∠D,延长BA至点E,连接CE,且CE交AD于点F,∠EAD和∠ECD的角平分线相交于点P.
(1)①直接写出AB和CD的位置关系: ;
②求证:∠EAD∠ECD=∠APC.
(2)若∠B=70°,∠E=60°,求∠APC的度数;
(3)若∠APC=m°,∠EFD=n°,请你探究m和n之间的数量关系.
【变式7-3】(2021春 东坡区校级期末)如图,四边形ABCD,BE、DF分别平分四边形的外角∠MBC和∠NDC,若∠BAD=α,∠BCD=β.
(1)如图1,若α+β=120°,求∠MBC+∠NDC的度数;
(2)如图1,若BE与DF相交于点G,∠BGD=30°,请写出α、β所满足的等量关系式;
(3)如图2,若α=β,判断BE、DF的位置关系,并说明理由.
【题型8 内外角角平分线模型】
【条件】△ABC中,BP、CP分别是△ABC的内角和外角的角平分线,且相交于点P.
【结论】
【证明】 ∵BP是∠ABC平分线,∴ ∵CP是∠ACE平分线,∴
由△ABC外角定理可知:∠ACE=∠ABC+∠A即:2∠1=2∠3+∠A ……①
对①式两边同时除以2,得:∠1=∠3+ ……②又在△BPC中由外角定理可知:∠1=∠3+∠P ……③
比较②③式子可知:.==.
【例8】(2021春 靖江市校级月考)如图①,△ABC中,BD平分∠ABC,且与△ABC的外角∠ACE的角平分线交于点D.
(1)若∠ABC=70°,∠ACB=40°,求∠D的度数;
(2)若把∠A截去,得到四边形MNCB,如图②,猜想∠D、∠M、∠N的关系,并说明理由.
【变式8-1】(2020春 兴化市期中)(1)思考探究:如图,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,已知∠ABC=70°,∠ACD=100°.求∠A和∠P的度数;
(2)类比探究:如图,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,已知∠P=n°.求∠A的度数(用含n的式子表示);
(3)拓展迁移:已知,在四边形ABCD中,四边形ABCD的内角∠ABC与外角∠DCE的平分线所在直线相交于点P,∠P=n°,请画出图形;并探究出∠A+∠D的度数(用含n的式子表示).
【变式8-2】(2020秋 平舆县期中)已知:如图,∠MON=90°,点A、B分别在射线OM、ON上移动(不与点O重合),AC平分∠MAB,AC的反向延长线与∠ABO的平分线相交于点D.
(1)当∠ABO=70°时、∠D的度数是多少?
(2)随着点A、B的移动,试问∠D的大小是否变化?请说出你的理由.
【变式8-3】(2020春 惠安县期末)在△ABC中,∠ACB的平分线CD与外角∠EAC的平分线AF所在的直线交于点D.
(1)如图1,若∠B=60°,求∠D的度数;
(2)如图2,把△ACD沿AC翻折,点D落在D′处.
①当AD′⊥AD时,求∠BAC的度数;
②试确定∠DAD′与∠BAC的数量关系,并说明理由.
角度计算中的经典模型
【题型1 双垂直模型】
【条件】∠B=∠D=∠ACE=90°.
【结论】∠BAC=∠DCE,∠ACB=∠CED.
【证明】∵∠B=∠D=∠ACE=90°;∴∠BAC+∠ACB=90°;又∠ECD+∠ACB=90°;∴∠BAC=∠DCE
同理,∠ACB+∠DCE =90°,且∠CED+∠DCE =90°;∴∠ACB=∠CED,得证.
【例1】(2020秋 铁西区期中)(1)如图①,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,求证:∠ACD=∠B;
(2)如图②,在Rt△ABC中,∠C=90°,D、E分别在AC,AB上,且∠ADE=∠B,判断△ADE的形状?并说明理由?
(3)如图③,在Rt△ABC和Rt△DBE中,∠C=90°,∠E=90°,点C,B,E在同一直线上,若AB⊥BD,AB=BD,则CE与AC,DE有什么等量关系,并证明.
【解题思路】(1)根据直角三角形的性质得出∠ACD+∠A=∠B+∠DCB=90°,再解答即可;
(2)根据直角三角形的性质得出∠ADE+∠A=∠A+∠B=90°,再解答即可;
(3)根据直角三角形的性质得出∠ABC+∠A=∠ABC+∠DBE=∠DBE+∠D=90°,再解答即可.
【解答过程】证明:(1)∵在Rt△ABC中,∠ACB=90°,CD⊥AB,
∴∠ACD+∠A=∠B+∠DCB=90°,
∴∠ACD=∠B;
(2)△ADE是直角三角形.
∵在Rt△ABC中,∠C=90°,D、E分别在AC,AB上,且∠ADE=∠B,∠A为公共角,
∴∠AED=∠ACB=90°,
∴△ADE是直角三角形;
(3)CE=AC+DE,理由如下:
∵在Rt△ABC和Rt△DBE中,∠C=90°,∠E=90°,AB⊥BD,
∴∠ABC+∠A=∠ABC+∠DBE=∠DBE+∠D=90°,
∴∠A=∠DBE,∠ABC=∠BDE,
在△ABC与△BDE中
,
∴△ABC≌△BDE(ASA),
∴CB=DE,BE=AC,
∴CE=BC+BE=AC+DE;
【变式1-1】(2021春 盐城期末)已知:如图,在△ABC中,∠ACB=90°,CE⊥AB,F为边BC上一点,连接AF交CE于点G,∠CGF=∠CFG.求证:AF平分∠BAC.
【解题思路】由三角形的内角和定理结合垂直的定义可求得∠CAF+∠CFG=90°,∠AGE+∠FAE=90°,进而可得∠CAF=∠FAE,即可证明结论.
【解答过程】解:∵∠ACB=90°,∠CAF+∠ACB+∠CFG=180°,
∴∠CAF+∠CFG=90°,
∵CE⊥AB,
∴∠AEC=90°,
∵∠AEC+∠AGE+∠FAE=180°,
∴∠AGE+∠FAE=90°,
∵∠AGE=∠CGF=∠CFG,
∴∠CAF=∠FAE,
∴AF平分∠BAC.
【变式1-2】(2020秋 丰城市期中)(1)如图①,△ABC是锐角三角形,高BD,CE相交于点H,找出∠BHC和∠A之间存在何种等量关系;并证明你的结论
(2)如图②,若△ABC是钝角三角形,∠A>90°,高BD,CE所在的直线相交于点H,请你判断此时(1)中的等量关系是否仍然成立?并说明理由.
【解题思路】(1)根据对顶角的性质,可得∠BHC与∠EHD的关系,根据四边形的内角和定理,可得答案;
(2)根据对顶角的性质,可得∠BHC与∠EHD的关系,根据四边形的内角和定理,可得答案.
【解答过程】解:(1)∵BD⊥AC,
∴∠ADB=90°,
∵CE⊥AB,
∴∠AEC=90°,
∵∠A+∠ADB+∠AEC+∠DHE=360°,
∴∠DHE=360﹣(∠A+∠ADB+∠AEC)=360﹣(∠A+90+90)=180﹣∠A
∴∠BHC=∠DHE=180﹣∠A
(2)∵BD⊥AC,
∴∠ADH=90°
∵CE⊥AB,
∴∠AEH=90°
∵∠DAE+∠ADH+∠AEH+∠BHC=360
∴∠BHC=360﹣(∠DAE+∠ADH+∠AEH)=360﹣(∠DAE+90+90)=180﹣∠DAE
∴∠BHC=180﹣∠A
【变式1-3】(2021春 庐江县期末)如图1,AB⊥BC于点B,CD⊥BC于点C,点E在线段BC上,且AE⊥DE.
(1)求证:∠EAB=∠CED;
(2)如图2,AF、DF分别平分∠BAE和∠CDE,则∠F的度数是 (直接写出答案即可);
(3)如图3,EH平分∠CED,EH的反向延长线交∠BAE的平分线AF于点G.求证:EG⊥AF.(提示:三角形内角和等于180°)
【解题思路】(1)根据垂直得到直角三角形,由直角三角形两锐角互余利用等量代换证明结论;
(2)通过作FM∥AB∥CD可证∠DFA=∠CDF+∠BAF,因为∠CDE+∠BAE=90°和角平分线的定义可得∠F(∠CDE+∠BAE),继而得到答案;
(3)根据角平分线的定义得∠CEH=∠DEH=∠GEB=∠BAG=∠EAF,由于∠B=90°,∠BAE+∠BEA=90°,在△AEG中,可证得∠EAG+∠AEG=90°,从而证得结论.
【解答过程】(1)证明:∵AB⊥BC,CD⊥BC,
∴∠B=∠C=90°,
∴∠BAE+∠AEB=90°,
∵AE⊥DE,
∴∠AED=90°,
∴∠AEB+∠CED=90°,
∴∠BAE=∠CED.
(2)解:答案为45°;
过点F作FM∥AB,如图,
∵AB⊥BC,CD⊥BC,
∴∠B=∠C=90°,
∴AB∥CD,
∵∠C=90°,
∴∠CED+∠CDE=90°,
∵∠BAE=∠CED,
∴∠BAE+∠CDE=90°,
∵AF、DF分别平分∠BAE和∠CDE,
∴∠CDF∠CDE,∠BAF∠BAE,
∴∠CDF+∠BAF(∠BAE+∠CDE)=45°,
∵FM∥AB∥CD,
∴∠CDF=∠DFM,∠BAF=∠AFM,
∴∠AFD=∠CDF+∠BAF=45°.
(3)∵EH平分∠CED,
∴∠CEH∠CED,
∴∠BEG∠CED,
∵AF平分∠BAE,
∴∠BAG∠BAE,
∵∠BAE=∠CED,
∴∠BAG=∠BEG,
∵∠BAE+∠BEA=90°,
∴∠BAG+∠GAE+∠AEB=90°,
即∠GAE+∠AEB+∠BEG=90°,
∴∠AGE=90°,
∴EG⊥AF.
【题型2 A字模型】
【条件】△ADE与△ABC.
【结论】∠AED+∠ADE=∠B+C.
【证明】根据三角形内角和可得,∠AED+∠ADE=180°-∠A,∠B+C=180°-∠A,
∴∠AED+∠ADE=∠B+C,得证.
【例2】(2021春 资中县月考)如图所示,△ABC中,∠C=75°,若沿图中虚线截去∠C,则∠1+∠2等于多少度?
【解题思路】根据三角形内角和定理求出∠A+∠B,根据多边形的内角和公式求出即可.
【解答过程】解:∵∠A+∠B+∠C=180°,
∴∠A+∠B=180°﹣∠C,
∵∠C=75°,
∴∠A+∠B=180°﹣75°=105°,
∵∠1+∠2+∠A+∠B=360°,
∴∠1+∠2=360°﹣(∠A+∠B),
∴∠1+∠2=360°﹣105°=255°.
【变式2-1】(2020春 长沙县校级期中)如图,已知∠A=40°,求∠1+∠2+∠3+∠4的度数.
【解题思路】根据三角形的内角和定理分别求得∠1+∠2,∠3+∠4,就可求得最后结果.
【解答过程】解:∵∠A=40°,
∴∠1+∠2=∠3+∠4=180°﹣∠A=140°.
∴∠1+∠2+∠3+∠4=280°.
【变式2-2】(2020春 常州期中)如图,△ABC中,∠B=68°,∠A比∠C大28°,点D、E分别在AB、BC上.连接DE,∠DEB=42°.
(1)求∠A的度数;
(2)判断DE与AC之间的位置关系,并说明理由.
【解题思路】(1)设∠C的度数为x,根据三角形的内角和列出方程解答即可;
(2)根据平行线的判定解答即可.
【解答过程】解:(1)设∠C的度数为x°,则∠A的度数为(x+28)°,
△ABC中,∠A+∠B+∠C=180°,∠B=68°,
可得:x+x+28+68=180,
解得:x=42,
所以∠C=42°,∠A=70°,
(2)∵∠DEB=42°,∠C=42°,
∴∠DEB=∠C,
∴DE∥AC.
【变式2-3】(2020春 新野县期末)旧知新意:
我们容易证明,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?
尝试探究:
(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?
初步应用:
(2)如图2,在△ABC纸片中剪去△CDE,得到四边形ABDE,∠1=130°,则∠2﹣∠C= ;
(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请利用上面的结论直接写出答案 .
【解题思路】(1)根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠DBC+∠ECB,再利用三角形内角和定理整理即可得解;
(2)根据(1)的结论整理计算即可得解;
(3)表示出∠DBC+∠ECB,再根据角平分线的定义求出∠PBC+∠PCB,然后利用三角形内角和定理列式整理即可得解;
【解答过程】解:(1)∠DBC+∠ECB
=180°﹣∠ABC+180°﹣∠ACB
=360°﹣(∠ABC+∠ACB)
=360°﹣(180°﹣∠A)
=180°+∠A;
(2)∵∠1+∠2=∠180°+∠C,
∴130°+∠2=180°+∠C,
∴∠2﹣∠C=50°;
(3)∠DBC+∠ECB=180°+∠A,
∵BP、CP分别平分外角∠DBC、∠ECB,
∴∠PBC+∠PCB(∠DBC+∠ECB)(180°+∠A),
在△PBC中,∠P=180°(180°+∠A)=90°∠A;
即∠P=90°∠A;
故答案为:50°,∠P=90°∠A;
【题型3 8字模型】
【条件】AD、BC相交于点O.
【结论】∠A+∠B=∠C+∠D.(上面两角之和等于下面两角之和)
【证明】在△ABO中,由内角和定理:∠A+∠B+∠BOA=180°,在△CDO中,∠C+∠D+∠COD=180°,
∴∠A+∠B+∠BOA=180°=∠C+∠D+∠COD,由对顶角相等:∠BOA=∠COD
∴∠A+∠B=∠C+∠D,得证.
【例3】(2020秋 庆阳期中)【问题背景】(1)如图1的图形我们把它称为“8字形”,请说明∠A+∠B=∠C+∠D;
【问题探究】
(2)如图2,直线AP平分△BAO的外角∠FAD,CP平分△OCD的外角∠BCE,若∠ABC=32°,∠ADC=22°,求∠P的度数.
【解题思路】(1)根据三角形内角和定理即可证明.
(2)由AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,推出∠1=∠2,∠3=∠4,推出∠PAD=180°﹣∠2,∠PCD=180°﹣∠3,由∠P+(180°﹣∠1)=∠D+(180°﹣∠3),∠P+∠1=∠B+∠4,推出2∠P=∠B+∠D,即可解决问题.
【解答过程】(1)证明:在△AOB中,∠A+∠B+∠AOB=180°,
在△COD中,∠C+∠D+∠COD=180°,
∵∠AOB=∠COD,
∴∠A+∠B=∠C+∠D;
(2)如图2,
∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,
∴∠1=∠2,∠3=∠4,
∴∠PAD=180°﹣∠2,∠PCD=180°﹣∠3,
∵∠P+(180°﹣∠1)=∠D+(180°﹣∠3),∠P+∠1=∠B+∠4,
∴2∠P=∠B+∠D,
∴∠P(∠B+∠D)(32°+22°)=27°.
【变式3-1】(2021春 江阴市校级月考)如图1,已知线段AB、CD相交于点O,连接AC、BD,则我们把形如这样的图形称为“8字型”.
(1)求证:∠A+∠C=∠B+∠D;
(2)如图2,若∠CAB和∠BDC的平分线AP和DP相交于点P,与CD、AB分别相交于点M、N.
①以线段AC为边的“8字型”有 个,以点O为交点的“8字型”有 个;
②若∠B=100°,∠C=120°,求∠P的度数;
③若角平分线中角的关系改为“∠CAB=3∠CAP,∠CDB=3∠CDP”,试探究∠P与∠B、∠C之间存在的数量关系,并证明理由.
【解题思路】(1)根据三角形的内角和即可得到结论;
(2)①以线段AC为边的”8字型“有3个,以点O为交点的”8字型“有4个;
②根据角平分线的定义得到∠CAP=∠BAP,∠BDP=∠CDP,再由”8字型“得到∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,两等式相减得到∠C﹣∠P=∠P﹣∠B,即∠P(∠C+∠B),最后把∠C=120°,∠B=100°代入计算即可;
③与②的证明方法一样得到3∠P=∠B+2∠C.
【解答过程】解:(1)证明:在图1中,有∠A+∠C=180°﹣∠AOC,∠B+∠D=180°﹣∠BOD,
∵∠AOC=∠BOD,
∴∠A+∠C=∠B+∠D;
(2)解:①3;4;
故答案为:3,4;
②以M为交点”8字型“中,有∠P+∠CDP=∠C+∠CAP,
以N为交点”8字型“中,有∠P+∠BAP=∠B+∠BDP
∴2∠P+∠BAP+∠CDP=∠B+∠C+∠CAP+∠BDP,
∵AP、DP分别平分∠CAB和∠BDC,
∴∠BAP=∠CAP,∠CDP=∠BDP,
∴2∠P=∠B+∠C,
∵∠B=100°,∠C=120°,
∴∠P(∠B+∠C)(100°+120°)=110°;
③3∠P=∠B+2∠C,其理由是:
∵∠CAB=3∠CAP,∠CDB=3∠CDP,
∴∠BAP∠CAB,∠BDP∠CDB,
以M为交点”8字型“中,有∠P+∠CDP=∠C+∠CAP,
以N为交点”8字型“中,有∠P+∠BAP=∠B+∠BDP
∴∠C﹣∠P=∠CDP﹣∠CAP(∠CDB﹣∠CAB),
∠P﹣∠B=∠BDP﹣∠BAP(∠CDB﹣∠CAB).
∴2(∠C﹣∠P)=∠P﹣∠B.
∴3∠P=∠B+2∠C.
【变式3-2】(2021春 侯马市期末)(1)已知:如图①的图形我们把它称为“8字形”,试说明:∠A+∠B=∠C+∠D.
(2)如图②,AP,CP分别平分∠BAD,∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的度数.
(3)如图(3),直线AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的数量关系是 ;
(4)如图(4),直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的数量关系是 .
【解题思路】(1)根据三角形的内角和等于180°列式整理即可得证;
(2)根据角平分线的定义可得∠1=∠2,∠3=∠4,再根据(1)的结论列出整理即可得解;
(3)表示出∠PAD和∠PCD,再根据(1)的结论列出等式并整理即可得解;
(4)根据四边形的内角和等于360°可得(180°﹣∠1)+∠P+∠4+∠B=360°,∠2+∠P+(180°﹣∠3)+∠D=360°,然后整理即可得解.
【解答过程】解:(1)∵∠A+∠B+∠AOB=180°,∠C+∠D+∠COD=180°,
∴∠A+∠B+∠AOB=∠C+∠D+∠COD.
∵∠AOB=∠COD,
∴∠A+∠B=∠C+∠D.
(2)∵AP,CP分别平分∠BAD,∠BCD,
∴∠BAP=∠PAD,∠BCP=∠PCD,
由(1)的结论得,∠P+∠BCP=∠ABC+∠BAP,①,
∠P+∠PAD=∠ADC+∠PCD②,
①+②得,2∠P+∠BCP+∠PAD=∠BAP+∠PCD+∠ABC+∠ADC,
∴2∠P=∠ABC+∠ADC,
∵∠ABC=36°,∠ADC=16°,
∴∠P=26°.
(3)∵直线AP平分∠BAD,CP平分∠BCD的外角∠BCE,
∴∠PAB=∠PAD,∠PCB=∠PCE,
∴2∠PAB+∠B=180°﹣2∠PCB+∠D,
∴180°﹣2(∠PAB+∠PCB)+∠D=∠B,
∵∠P+∠PAD=∠PCB+∠AOC=∠PCB+∠B+2∠PAD,
∴∠P=∠PAD+∠B+∠PCB=∠PAB+∠B+∠PCB,
∴∠PAB+∠PCB=∠P﹣∠B,
∴180°﹣2(∠P﹣∠B)+∠D=∠B,即∠P=90°(∠B+∠D).
故答案为:∠P=90°(∠B+∠D).
(4)∵直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,
∴∠FAP=∠PAO,∠PCE=∠PCB,
在四边形APCB中,(180°﹣∠FAP)+∠P+∠PCB+∠B=360°①,
在四边形APCD中,∠PAD+∠P+(180°﹣∠PCE)+∠D=360°②,
①+②得:2∠P+∠B+∠D=360°,
∴∠P=180°(∠B+∠D).
故答案为:∠P=180°(∠B+∠D).
【变式3-3】(2021春 高新区校级月考)(1)如图1的图形我们把它称为“8字形”,请说明:∠A+∠B=∠C+∠D.
(2)阅读下面的内容,并解决后面的问题:
(①)如图2,AP、CP分别平分∠BAD、∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的度数.
(②)如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想∠P的度数,并说明理由.
(③)如图4中,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论,无需说明理由.
【解题思路】(1)根据三角形的内角和等于180°列式整理即可得证;
(2)①根据角平分线的定义可得∠1=∠2,∠3=∠4,再根据(1)的结论列出整理即可得解;
②表示出∠PAD和∠PCD,再根据(1)的结论列出等式并整理即可得解;
③根据四边形的内角和等于360°可得(180°﹣∠1)+∠P+∠4+∠B=360°,∠2+∠P+(180°﹣∠3)+∠D=360°,然后整理即可得解.
【解答过程】解:(1)∵∠A+∠B+∠AOB=180°,∠C+∠D+∠COD=180°,
∴∠A+∠B+∠AOB=∠C+∠D+∠COD,
∵∠AOB=∠COD,
∴∠A+∠B=∠C+∠D;
(2)①如图2:∵AP、CP分别平分∠BAD、∠BCD
∴∠1=∠2,∠3=∠4,
由(1)的结论得:∠P+∠3=∠2+∠B①,
∠P+∠1=∠4+∠D②,
①+②,得2∠P+∠1+∠3=∠2+∠4+∠B+∠D,
∵∠ABC=36°,∠ADC=16°,
∴∠P(∠B+∠D)=26°.
②∠P=26°.
如图3:∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,
∴∠1=∠2,∠3=∠4,
由(1)的结论得:∠PAD+∠P=∠PCD+∠D①,∠PAB+∠P=∠PCB+∠B②,
∵∠PAB=∠1,∠1=∠2,
∴∠PAB=∠2,
∴∠2+∠P=∠3+∠B③,
①+③得∠2+∠P+∠PAD+∠P=∠3+∠B+∠PCD+∠D,即2∠P+180°=∠B+∠D+180°,
∴∠P(∠B+∠D )=26°.
③如图4,
∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,
∴∠1=∠2,∠3=∠4,
∴(180°﹣2∠1)+∠B=(180°﹣2∠4)+∠D,
在四边形APCB中,(180°﹣∠1)+∠P+∠4+∠B=360°,
在四边形APCD中,∠2+∠P+(180°﹣∠3)+∠D=360°,
∴2∠P+∠B+∠D=360°,
∴∠P=180°(∠B+∠D).
【题型4 飞镖模型】
【条件】四边形ABDC如上左图所示.
【结论】∠D=∠A+∠B+∠C.(凹四边形凹外角等于三个内角和)
【证明】如上右图,连接AD并延长到E,则:
∠BDC=∠BDE+∠CDE=(∠B+∠1)+(∠2+∠C)=∠B+∠BAC+∠C.本质为两个三角形外角和定理证明.
【例4】(2020春 汝阳县期末)阅读下列材料,然后解答后面的问题.
(1)定义:把四边形的某些边向两方延长,其他各边有不在延长所得直线的同一旁,这样的四边形叫做凹四边形.如图1,四边形ABCD为凹四边形.
(2)性质探究:请完成凹四边形一个性质的证明.
已知:如图2,四边形ABCD是凹四边形.
求证:∠BCD=∠B+∠A+∠D.
(3)性质应用:
如图3,在凹四边形ABCD中,∠BAD的角平分线与∠BCD的角平分线交于点E,若∠ADC=140°,∠AEC=102°,则∠B= °.
【解题思路】(2)延长BC交AD于点M,根据三角形的外角的性质即可解决问题.
(3)利用(2)中结论如图3中,设∠B=x,∠ECB=∠ECD=α,∠EAD=∠EAB=β,列出方程组即可解决问题.
【解答过程】解:(2)延长BC交AD于点M
∵∠BCD是△CDM的外角,
∴∠BCD=∠CMD+∠D,
同理∠CMD是△ABM的外角,
∴∠CMD=∠A+∠B,
∴∠BCD=∠A+∠B+∠D;
(3)如图3中,设∠B=x,∠ECB=∠ECD=α,∠EAD=∠EAB=β.
由(2)可知,,
解得x=64°
故答案为64.
【变式4-1】(2020秋 白银期末)(1)探究:如图1,求证:∠BOC=∠A+∠B+∠C.
(2)应用:如图2,∠ABC=100°,∠DEF=130°,求∠A+∠C+∠D+∠F的度数.
【解题思路】(1)作射线OA,由三角形外角的性质可知∠1+∠B=∠3,∠2+∠C=∠4,两式相加即可得出结论;
(2)连接AD,由(1)的结论可知∠F+∠2+∠3=∠DEF,∠1+∠4+∠C=∠ABC,两式相加即可得出结论.
【解答过程】解:(1)作射线OA,
∵∠3是△ABO的外角,
∴∠1+∠B=∠3,①
∵∠4是△AOC的外角,
∴∠2+∠C=∠4,②
①+②得,∠1+∠B+∠2+∠C=∠3+∠4,
即∠BOC=∠A+∠B+∠C;
(2)连接AD,同(1)可得,∠F+∠2+∠3=∠DEF③,∠1+∠4+∠C=∠ABC④,
③+④得,∠F+∠2+∠3+∠1+∠4+∠C=∠DEF+∠ABC=130°+100°=230°,
即∠A+∠C+∠D+∠F=230°.
【变式4-2】(2020秋 黄石港区校级期中)如图,(1)求证:∠ABC=∠A+∠C+∠ADC;
(2)若∠A=52°,∠C=20°,BE、DE分别平分∠ABC和∠ADC,交于点E,求∠E的度数.
【解题思路】(1)连接DB,延长DB到T.利用三角形的外角的性质证明即可.
(2)利用(1)中结论,以及“8字型”的性质解决问题即可.
【解答过程】(1)证明:连接DB,延长DB到T.
∵∠ABT=∠A+∠ADB,∠CBT=∠C+∠CDB,
∴∠ABC=∠ABT+∠CBT=∠A+∠ADB+∠CDB+∠C=∠A+∠ADC+∠C.
(2)解:设DE交AB于点O.
∵∠ABC=∠A+∠ADC+∠C,BE平分∠ABC,
∴∠OBE∠ABC(∠A+∠ADC+∠C),
∵∠A+∠ADO=∠E+∠OBE,
∴∠E=∠A+∠ADO﹣∠OBE,
∵DE平分∠ADC,
∴∠ADE∠ADC,
∴∠E=∠A∠ADC(∠A+∠ADC+∠C)(∠A﹣∠C)=16°.
【变式4-3】(2020春 福山区期中)直线在同一平面内有平行和相交两种位置关系,线段首尾连接可以变换出很多不同的图形,这些不同的角又有很多不同关系,今天我们就来探究一下这些奇妙的图形吧!
【问题探究】
(1)如图1,请直接写出∠A+∠B+∠C+∠D+∠E= ;
(2)将图1变形为图2,∠A+∠DBE+∠C+∠D+∠E的结果如何?请写出证明过程;
(3)将图1变形为图3,则∠A+∠B+∠C+∠D+∠E的结果如何?请写出证明过程.
【变式拓展】
(4)将图3变形为图4,已知∠BGF=160°,那么∠A+∠B+∠C+∠D+∠E+∠F的度数是 .
【解题思路】(1)根据三角形外角的性质,得到∠2=∠C+∠E,∠1=∠A+∠2,根据三角形内角和等于180°即可求解.
(2)根据三角形外角的性质,得到∠ABE=∠C+∠E,∠DBC=∠A+∠D,即可证明此结论.
(3)根据三角形外角的性质,得到∠DFG=∠B+∠E,∠FGD=∠A+∠C,即可证明此结论;
(4)根据三角形外角的性质,得到∠BGF=∠B+∠2=160°,∠2=∠D+∠F,∠BGF=∠1+∠E=160°,∠1=∠A+∠C,即可得到结论.
【解答过程】(1)解:如图1,∵∠2=∠C+∠E,∠1=∠A+∠2,
∴∠A+∠B+∠C+∠D+∠E=∠1+∠B+∠D=180°,
故答案为:180°;
(2)证明:∵∠ABE=∠C+∠E,∠DBC=∠A+∠D,
∠ABE+∠DBE+∠DBC=180°,
∴∠A+∠DBE+∠C+∠D+∠E=180°
∴将图①变形成图②∠A+∠DBE+∠C+∠D+∠E仍然为180°;
(3)证明:∵在△FGD中,∠DFG+∠FGD+∠D=180°,
∠DFG=∠B+∠E,∠FGD=∠A+∠C,
∴∠A+∠B+∠C+∠D+∠E=180°,
∴将图①变形成图③,则∠A+∠B+∠C+∠D+∠E还为180°;
(4)解:∵∠BGF=∠B+∠2=160°,∠2=∠D+∠F,
∴∠B+∠D+∠F=160°,
∵∠BGF=∠1+∠E=160°,∠1=∠A+∠C,
∴∠A+∠C+∠E=160°,
∴∠A+∠B+∠C+∠D+∠E+∠F=320°,
故答案为:320°.
【题型5 风筝模型】
【条件】四边形ABPC,分别延长AB、AC于点D、E,如上左图所示.
【结论】∠PBD+∠PCE=∠A+∠P.
【证明】如上右图,连接AP,则:∠PBD=∠PAB+∠APB,∠PCE=∠PAC+∠APC,
∴∠PBD+∠PCE=∠PAB+∠APB+∠PAC+∠APC=∠BAC+∠BPC,得证.
【例5】(2020春 灌云县期中)如图,将△ABC的一角折叠,使点C落在△ABC内一点
(1)若∠1=40°,∠2=30°,求∠C的度数;
(2)试通过第(1)问,直接写出∠1、∠2、∠C三者之间的关系.
【解题思路】(1)根据折叠的性质可以得到,∠C′DE=∠CDE,∠C′ED=∠CED,根据平角定义得出∠1+∠C′DC=180°,∠2+∠C′EC=180°,求出∠C′DC+∠C′EC,在四边形C′DCE中,根据内角和定理求出即可;
(2)根据(1)的结果即可得出答案.
【解答过程】解:(1)∵△C′DE是由△CDE折叠而成,
∴∠C=∠C′,∠C′DE=∠CDE,∠C′ED=∠CED,
又∠1+∠C′DC=180°,∠2+∠C′EC=180°,
∴∠C′DC+∠C′EC=360°﹣(∠1+∠2)=290°,
又四边形C′DCE的内角和为360°,
∴∠C′+∠C=70°,
∴∠C=35°.
(2)2∠C=1+∠2,
理由是:∵△C′DE是由△CDE折叠而成,
∴∠C=∠C′,∠C′DE=∠CDE,∠C′ED=∠CED,
又∠1+∠C′DC=180°,∠2+∠C′EC=180°,
∴∠C′DC+∠C′EC=360°﹣(∠1+∠2),
又四边形C′DCE的内角和为360°,
∴∠C′+∠C=360°﹣[360°﹣(∠1+∠2)],
即∠C′+∠C=∠1+∠2,
∵∠C′=∠C
∴2∠C=∠1+∠2.
【变式5-1】(2020秋 路北区期中)如图,在△ABC中,D、E分别是边AB、AC上一点,将△ABC沿DE折叠,使点A落在边BC上.若∠A=55°,求∠1+∠2+∠3+∠4四个角和的度数?
【解题思路】依据三角形内角和定理,可得△ABC中,∠B+∠C=125°,即可得出∠1+∠2+∠3+∠4的度数.
【解答过程】解:∵∠A=55°,
∴△ABC中,∠B+∠C=125°,
又∵∠1+∠2+∠B=180°,∠3+∠4+∠C=180°,
∴∠1+∠2+∠3+∠4=360°﹣(∠B+∠C)=360°﹣125°=235°.
【变式5-2】(2020春 迁安市期末)动手操作:
一个三角形的纸片ABC,沿DE折叠,使点A落在点Aˊ处.
观察猜想
(1)如图1,若∠A=40°,则∠1+∠2= °;
若∠A=55°,则∠1+∠2= °;
若∠A=n°,则∠1+∠2= °.
探索证明:
(2)利用图1,探索∠1、∠2与∠A有怎样的关系?请说明理由.
拓展应用
(3)如图2,把△ABC折叠后,BA′平分∠ABC,CA′平分∠ACB,若∠1+∠2=108°,利用(2)中结论求∠BA′C的度数.
【解题思路】(1)根据翻折变换的性质用∠1、∠2表示出∠ADE和∠AED,再根据三角形的内角和定理列式整理即可得解;根据翻折变换的性质用∠1、∠2表示出∠ADE和∠AED,再根据三角形的内角和定理列式整理即可得解;
(2)由∠BDE、∠CED是△ADE的两个外角知∠BDE=∠A+∠AED、∠CED=∠A+∠ADE,据此得∠BDE+∠CED=∠A+∠AED+∠A+∠ADE,继而可得答案;
(3)由(1)∠1+∠2=2∠A知∠A=54°,根据BA'平分∠ABC,CA'平分∠ACB知∠A'BC+∠A'CB(∠ABC+∠ACB)=90°∠A.利用∠BA'C=180°﹣(∠A'BC+∠A'CB)可得答案.
【解答过程】解:(1)∵点A沿DE折叠落在点A′的位置,
∴∠ADE=∠A′DE,∠AED=∠A′ED,
∴∠ADE(180°﹣∠1),∠AED(180°﹣∠2)
在△ADE中,∠A+∠ADE+∠AED=180°,
∴40°(180°﹣∠1)(180°﹣∠2)=180°,
整理得∠1+∠2=80°;
同理∠A=55°,则∠1+∠2=110°;∠A=n°,则∠1+∠2=2n°;
故答案为:80°;110°;2n°;
(2)∠1+∠2=2∠A,
理由:∵∠BDE、∠CED是△ADE的两个外角,
∴∠BDE=∠A+∠AED,∠CED=∠A+∠ADE,
∴∠BDE+∠CED=∠A+∠AED+∠A+∠ADE,
∴∠1+∠ADE+∠2+∠AED=2∠A+∠AED+∠ADE,
即∠1+∠2=2∠A;
(3)由(1)∠1+∠2=2∠A,得2∠A=108°,
∴∠A=54°,
∵BA'平分∠ABC,CA'平分∠ACB,
∴∠A'BC+∠A'CB(∠ABC+∠ACB)
(180°﹣∠A)
=90°∠A.
∴∠BA'C=180°﹣(∠A'BC+∠A'CB),
=180°﹣(90°∠A)
=90°∠A
=90°54°
=117°.
【变式5-3】(2021春 高邮市校级期末)直角△ABC中,∠C=90°,点D,E分别是边AC,BC上的点,点P是一动点,令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在线段AB上,如图1所示,且∠α=50°,则∠1+∠2= ;
(2)若点P在边AB上运动,如图2所示,则∠α、∠1、∠2之间有何关系,并说明理由;
(3)如图3,若点P在斜边BA的延长线上运动(CE<CD),请写出∠α、∠1、∠2之间的关系式.
【解题思路】(1)根据四边形内角和定理以及邻补角的定义得出∠1+∠2=∠C+∠α,进而得出即可;
(2)利用(1)中所求得出答案即可;
(3)利用三角外角的性质分三种情况讨论即可.
【解答过程】解:(1)∵∠1+∠2+∠CDP+∠CEP=360°,∠C+∠α+∠CDP+∠CEP=360°,
∴∠1+∠2=∠C+∠α,
∵∠C=90°,∠α=50°,
∴∠1+∠2=140°;
(2)由(1)得出:
∠α+∠C=∠1+∠2,
∴∠1+∠2=90°+α.
(3)如图,
分三种情况:在BA延长线上取点P,连接EP、DP,
如图1,由三角形的外角性质,∠2=∠C+∠1+∠α,
∴∠2﹣∠1=90°+∠α;
如图2,∠α=0°,∠2=∠1+90°;
如图3,∠2=∠1﹣∠α+∠C,
∴∠1﹣∠2=∠α﹣90°.
【题型6 两内角角平分线模型】
【条件】△ABC中,BI、CI分别是∠ABC和∠ACB的角平分线,且相交于点I.
【结论】
【证明】∵BI是∠ABC平分线,∴∵CI是∠ACB平分线,∴
由A→B→I→C→A的飞镖模型可知:
∠I=∠A+∠2+∠3=∠A++=∠A+=.
【例6】(2020春 兴化市月考)如图,△ABC的角平分线BD、CE相交于点P.
(1)若∠ABC=50°,∠ACB=70°,则∠A= °;
(2)若∠A=80°,试求∠BPC的度数;
(3)试直接写出∠DPC与∠A之间的数量关系:∠DPC= .
【解题思路】先根据角平分线的定义得到∠1∠ABC,∠2∠ACB,再根据三角形内角和定理得∠BPC=180°﹣∠1﹣∠2=180°(∠ABC+∠ACB),加上∠ABC+∠ACB=180°﹣∠A,易得∠BPC=90°∠A,然后根据此结论解决各小题.
【解答过程】解:∵∠ABC,∠ACB的平分线相交于点P,
∴∠1∠ABC,∠2∠ACB,
∴∠BPC=180°﹣∠1﹣∠2=180°∠ABC∠ACB=180°(∠ABC+∠ACB),
∵∠ABC+∠ACB=180°﹣∠A,
∴∠BPC=180°(180°﹣∠A)=90°∠A,
(1)∵∠ABC=50°,∠ACB=70°,
∴∠A=180°﹣50°﹣70°=60°.
故答案为60.
(2)∵∠A=80°,
∴∠BPC=90°80°=130°;
(3)∵∠BPC=90°∠A,
∴∠DPC=180°﹣(90°∠A)=90°∠A.
故答案为:90°∠A.
【变式6-1】(2020秋 硚口区期中)如图,在Rt△ABC中,∠C=90°,BD平分∠ABC交AC于点D,AP平分∠BAC交BD于点P,∠BDC=58°,求∠BAP的度数.
【解题思路】先利用三角形内角和定理的推论,得出∠DBC=32°,再由角平分线的定义得到∠ABD=∠DBC=32°,求出∠ABC,再求出∠CAB即可解决问题.
【解答过程】解:∵∠BDC=58°,∠C=90°,
∴∠DBC=90°﹣∠BDC=32°,
∵BD平分∠ABC,
∴∠ABD=∠DBC=32°,
∴∠ABC=2∠ABD=64°,
∴∠CAB=90°﹣∠ABC=26°,
∵PA平分∠BAC,
∴∠BAP∠CAB=13°.
【变式6-2】(2020春 浦东新区期末)如图,点A、B分别在射线ON、OM上运动(不与点O重合),AC、BC分别是∠BAO和∠ABO的角平分线,BC延长线交ON于点G.
(1)若∠MON=60°,则∠ACB= °;若∠MON=90°,则∠ACB= °;
(2)若∠MON=n°.请求出∠ACG的度数;(用含n的代数式表示)
【解题思路】(1)由三角形内角和定理和角平分线的定义即可得到结论;
(2)由三角形内角和定理和角平分线的定义即可得到结论.
【解答过程】解:(1)∵∠MON=60°,
∴∠OBA+∠OAB=120°,
∵∠OBA、∠OAB的平分线交于点C,
∴∠ABC+∠BAC120°=60°,
∴∠ACB=180°﹣60°=120°,
∵∠MON=90°,
∴∠OBA+∠OAB=90°,
∵∠OBA、∠OAB的平分线交于点C,
∴∠ABC+∠BAC90°=45°,
∴∠ACB=180°﹣45°=135°;
(2)在△AOB中,∠OBA+∠OAB=180°﹣∠AOB=180°﹣n°,
∵∠OBA、∠OAB的平分线交于点C,
∴∠ABC+∠BAC(∠OBA+∠OAB)(180°﹣n°),
即∠ABC+∠BAC=90°n°,
∴∠ACB=180°﹣(∠ABC+∠BAC)=180°﹣(90°n°)=90°n°,
∴∠ACG=180°﹣(90°n°)=90°n°.
故答案为:120,135.
【变式6-3】(2020春 南岗区期末)已知在△ABC中,∠A=100°,点D在△ABC的内部连接BD,CD,且∠ABD=∠CBD,∠ACD=∠BCD.
(1)如图1,求∠BDC的度数;
(2)如图2,延长BD交AC于点E,延长CD交AB于点F,若∠AED﹣∠AFD=12°,求∠ACF的度数.
【解题思路】(1)依据三角形内角和定理以及角平分线的定义,即可得到∠BDC的度数;
(2)设∠ACF=α,则∠BCD=α,∠CBD=40°﹣α=∠ABD,依据三角形外角性质,即可得到∠AED=∠ACF+∠CDF,∠AFD=∠ABE+∠BDF,再根据∠AED﹣∠AFD=12°,即可得到α的值.
【解答过程】解:(1)∵∠A=100°,
∴∠ABC+∠ACB=80°,
又∵∠ABD=∠CBD,∠ACD=∠BCD,
∴∠CBD∠ABC,∠BCD∠ACB,
∴∠CBD+∠BCD(∠ABC+∠ACB)=40°,
∴∠BDC=180°﹣40°=140°;
(2)设∠ACF=α,则∠BCD=α,
∵∠BDC=140°,
∴∠CBD=40°﹣α=∠ABD,
∵∠AED是△DCE的外角,∠AFD是△BDF的外角,
∴∠AED=∠ACF+∠CDF,∠AFD=∠ABE+∠BDF,
∴∠AED﹣∠AFD=∠ACF+∠CDF﹣∠ABE﹣∠BDE=α﹣(40°﹣α)=12°,
解得α=26°,
∴∠ACF=26°.
【题型7 两外角角平分线模型】
【条件】△ABC中,BI、CI分别是△ABC的外角的角平分线,且相交于点O.
【结论】.
【证明】∵BO是∠EBC平分线,∴,∵CO是∠FCB平分线,∴
由△BCO中内角和定理可知:∠O=180°-∠2 -∠5 =180°--=180°--===.
【例7】(2020春 浦东新区期末)已知:如图,△ABC的两个外角的平分线交于点P,如果∠A=40°,求∠BPC的度数.
【解题思路】根据三角形内角和定理得到∠ABC+∠ACB=140°,根据角平分线的定义、三角形内角和定理计算即可.
【解答过程】解:∵∠A=40°,
∴∠ABC+∠ACB=180°﹣40°=140°,
∴∠EBC+∠FCB=360°﹣140°=220°,
∵BP、CP是△ABC的外角平分线,
∴∠PBC∠EBC,∠PCB∠FCB,
∴∠PBC+∠PCB(∠EBC+∠FCB)=110°,
∴∠BPC=180°﹣(∠PBC+∠PCB)=70°.
【变式7-1】(2020秋 鄂伦春自治旗月考)如图,△ABC中,分别延长△ABC的边AB、AC到D、E,∠CBD与∠BCE的平分线相交于点P,爱动脑筋的小明在写作业的时发现如下规律:
(1)若∠A=60°,则∠P= °;
(2)若∠A=40°,则∠P= °;
(3)若∠A=100°,则∠P= °;
(4)请你用数学表达式归纳∠A与∠P的关系 .
【解题思路】(1)若∠A=60°,则有∠ABC+∠ACB=120°,∠DBC+∠BCE=360°﹣120°=240°,根据角平分线的定义可以求得∠PBC+∠PCB的度数,再利用三角形的内角和定理即可求得∠P的度数.
(2)(3)和(1)的解题步骤相似.
(4)利用角平分线的性质和三角形的外角性质可求出∠BCP(∠A+∠ABC),∠CBP(∠A+∠ACB);再利用三角形内角和定理便可求出∠A与∠P的关系.
【解答过程】解:(1)∵∠A=60°,
∴∠ABC+∠ACB=180°﹣60°=120°,∠DBC+∠BCE=360°﹣120°=240°,
又∵∠CBD与∠BCE的平分线相交于点P,
∴∠PBC∠DBC,∠PCB∠BCE,
∴∠PBC+∠PCB(∠DBC+∠ECB)=120°,
∴∠P=60°.
同理得:(2)70°;
(3)40°
(4)∠P=90°∠A.理由如下:
∵BP平分∠DBC,CP平分∠BCE,
∴∠DBC=2∠CBP,∠BCE=2∠BCP
又∵∠DBC=∠A+∠ACB∠BCE=∠A+∠ABC,
∴2∠CBP=∠A+∠ACB,2∠BCP=∠A+∠ABC,
∴2∠CBP+2∠BCP=∠A+∠ACB+∠A+∠ABC=180°+∠A,
∴∠CBP+∠BCP=90°∠A
又∵∠CBP+∠BCP+∠P=180°,
∴∠P=90°∠A.
故答案为:60,70,40,90°∠A.
【变式7-2】(2020春 石城县期末)如图,在四边形ABCD中,AD∥BC,∠B=∠D,延长BA至点E,连接CE,且CE交AD于点F,∠EAD和∠ECD的角平分线相交于点P.
(1)①直接写出AB和CD的位置关系: ;
②求证:∠EAD∠ECD=∠APC.
(2)若∠B=70°,∠E=60°,求∠APC的度数;
(3)若∠APC=m°,∠EFD=n°,请你探究m和n之间的数量关系.
【解题思路】(1)①根据平行线的性质与判定解答即可;②过点P作PQ∥AB,则∠EAP=∠APQ,再根据平行线的性质证明即可;
(2)由AD∥BC,AB∥CD,可得∠EAD=∠B=70°,∠ECD=∠E=60°,再根据角平分线的性质解答即可;
(3)过点F作FH∥AB,根据平行线的性质以及角的和差关系解答即可.
【解答过程】解:(1)①∵AD∥BC,
∴∠EAD=∠B,
∵∠B=∠D,
∴∠EAD=∠D,
∴AB∥CD;
故答案为:AB∥CD;
②证明:过点P作PQ∥AB,则∠EAP=∠APQ,
∵AB∥CD,
∴PQ∥CD,
∴∠DCP=∠CPQ,
∵AB∥CD,
∴PQ∥CD,
∴∠DCP=∠CPQ,
∵∠EAP∠EAD,∠DCP∠ECD,
∴∠EAD∠ECD=∠APC.
(2)由(1)知AD∥BC,AB∥CD,
∴∠EAD=∠B=70°,∠ECD=∠E=60°,
由(1)知∠EAD+∠ECD=2∠APC,
∴∠APC(70°+60°)=65°;
(3)过点F作FH∥AB,则∠EAD=∠AFH,
∵AB∥CD,
∴FH∥CD,
∴∠ECD=∠CFH,
∴∠EAD+∠ECD=∠AFH+∠CFH=∠AFC=∠EFD,
由(1)知∠EAD+∠ECD=2∠APC,
∴∠EFD=2∠APC,
∵∠APC=m°,∠EFD=n°,
∴mn.
【变式7-3】(2021春 东坡区校级期末)如图,四边形ABCD,BE、DF分别平分四边形的外角∠MBC和∠NDC,若∠BAD=α,∠BCD=β.
(1)如图1,若α+β=120°,求∠MBC+∠NDC的度数;
(2)如图1,若BE与DF相交于点G,∠BGD=30°,请写出α、β所满足的等量关系式;
(3)如图2,若α=β,判断BE、DF的位置关系,并说明理由.
【解题思路】(1)∠ABC+∠ADC=360°﹣(α+β)=240°,则∠MBC+∠NDC=180°﹣∠ABC+180°﹣∠ADC=α+β=120°.
(2)连接BD,由(1)有,∠MBC+∠NDC=α+β,BE、DF分别平分四边形的外角∠MBC和∠NDC,则∠CBG+∠CDG∠MBC∠NDC(∠MBC+∠NDC)(α+β),在△BCD中,∠BDC+∠CBD=180°﹣∠BCD=180°﹣β,在△BDG中,∠GBD+∠GDB+∠BGD=180°,(∠CBG+∠CDG)+(∠BDC+∠CBD)+∠BGD=180°,则(α+β)+180°﹣β+30°=180°,即β﹣α=60°,
(3)由(1)有,∠MBC+∠NDC=α+β,BE、DF分别平分四边形的外角∠MBC和∠NDC,则∠CBE+∠CDH(α+β),∠CBE+β﹣∠DHB(α+β),根据α=β,则有∠CBE+β﹣∠DHB(β+β)=β,∠CBE=∠DHB,则BE∥DF.
【解答过程】解:(1)∵∠ABC+∠ADC=360°﹣(α+β)=240°,
∴∠MBC+∠NDC=180°﹣∠ABC+180°﹣∠ADC=α+β=120°.
(2)β﹣α=60°
理由:如图1,连接BD,
由(1)有,∠MBC+∠NDC=α+β,
∵BE、DF分别平分四边形的外角∠MBC和∠NDC,
∴∠CBG∠MBC,∠CDG∠NDC,
∴∠CBG+∠CDG∠MBC∠NDC(∠MBC+∠NDC)(α+β),
在△BCD中,∠BDC+∠CBD=180°﹣∠BCD=180°﹣β,
在△BDG中,∠GBD+∠GDB+∠BGD=180°,
∴∠CBG+∠CBD+∠CDG+∠BDC+∠BGD=180°,
∴(∠CBG+∠CDG)+(∠BDC+∠CBD)+∠BGD=180°,
∴(α+β)+180°﹣β+30°=180°,
∴β﹣α=60°,
(3)平行,
理由:如图2,延长BC交DF于H,
由(1)有,∠MBC+∠NDC=α+β,
∵BE、DF分别平分四边形的外角∠MBC和∠NDC,
∴∠CBE∠MBC,∠CDH∠NDC,
∴∠CBE+∠CDH∠MBC∠NDC(∠MBC+∠NDC)(α+β),
∵∠BCD=∠CDH+∠DHB,
∴∠CDH=∠BCD﹣∠DHB=β﹣∠DHB,
∴∠CBE+β﹣∠DHB(α+β),
∵α=β,
∴∠CBE+β﹣∠DHB(β+β)=β,
∴∠CBE=∠DHB,
∴BE∥DF.
【题型8 内外角角平分线模型】
【条件】△ABC中,BP、CP分别是△ABC的内角和外角的角平分线,且相交于点P.
【结论】
【证明】 ∵BP是∠ABC平分线,∴ ∵CP是∠ACE平分线,∴
由△ABC外角定理可知:∠ACE=∠ABC+∠A即:2∠1=2∠3+∠A ……①
对①式两边同时除以2,得:∠1=∠3+ ……②又在△BPC中由外角定理可知:∠1=∠3+∠P ……③
比较②③式子可知:.==.
【例8】(2021春 靖江市校级月考)如图①,△ABC中,BD平分∠ABC,且与△ABC的外角∠ACE的角平分线交于点D.
(1)若∠ABC=70°,∠ACB=40°,求∠D的度数;
(2)若把∠A截去,得到四边形MNCB,如图②,猜想∠D、∠M、∠N的关系,并说明理由.
【解题思路】(1)根据三角形内角和定理以及角平分线性质,先求出∠D、∠A的等式,推出∠A=2∠D,最后代入求出即可;
(2)根据(1)中的结论即可得到结论.
【解答过程】解:(1)∵∠ACE=∠A+∠ABC,
∴∠ACD+∠DCE=∠A+∠ABD+∠DBC,∠DCE=∠D+∠DBC,
又BD平分∠ABC,CD平分∠ACE,
∴∠ABD=∠DBE,∠ACD=∠ECD,
∴∠A=2(∠DCE﹣∠DBC),∠D=∠DCE﹣∠DBC,
∴∠A=2∠D,
∵∠ABC=70°,∠ACB=40°,
∴∠A=180°﹣∠ABC﹣∠ACB=70°,
∴∠D=35°;
(2)∠D(∠M+∠N﹣180°);
理由:延长BM、CN交于点A,
∵∠A+∠ANM+∠AMN=180°,∠AMN+∠BMN=180°,∠ANM+∠CNM=180°,
∴∠A=180°﹣∠ANM﹣∠AMN=180°﹣(180°﹣∠CNM)﹣(180°﹣∠BMN)=180°﹣180°+∠CNM﹣180°+∠BMN,
则∠A=∠BMN+∠CNM﹣180°,
由(1)知,∠D∠A,
∴∠D(∠BMN+∠CNM﹣180°).
【变式8-1】(2020春 兴化市期中)(1)思考探究:如图,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,已知∠ABC=70°,∠ACD=100°.求∠A和∠P的度数;
(2)类比探究:如图,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,已知∠P=n°.求∠A的度数(用含n的式子表示);
(3)拓展迁移:已知,在四边形ABCD中,四边形ABCD的内角∠ABC与外角∠DCE的平分线所在直线相交于点P,∠P=n°,请画出图形;并探究出∠A+∠D的度数(用含n的式子表示).
【解题思路】(1)根据三角形外角的性质可求∠A,根据角平分线的定义和三角形外角的性质可求∠P;
(2)根据三角形的一个外角等于与它不相邻的两个内角的和可得∠PCD=∠P+∠PBC,∠ACD=∠A+∠ABC,再根据角平分线的性质即可得解;
(3)添加辅助线,利用(2)中结论解决问题即可.
【解答过程】解:(1)∵∠ABC=70°,∠ACD=100°,
∴∠A=100°﹣70°=30°,
∵P点是∠ABC和外角∠ACD的角平分线的交点,
∴∠PCD∠ACD=50°,∠PBC∠ABC=35°,
∴∠P=50°﹣35°=15°;
(2)∠A=2n°.
理由:∵∠PCD=∠P+∠PBC,∠ACD=∠A+∠ABC,
∵P点是∠ABC和外角∠ACD的角平分线的交点,
∴∠ACD=2∠PCD,∠ABC=2∠PBC,
∴∠A+∠ABC=2(∠P+∠PBC),
∠A+∠ABC=2∠P+2∠PBC,
∠A+∠ABC=2∠P+∠ABC,
∴∠A=2∠P,
∴∠A=2n°;
(3)(Ⅰ)如图②延长BA交CD的延长线于F.
∵∠F=180°﹣∠FAD﹣∠FDA=180°﹣(180°﹣∠A)﹣(180°﹣∠D)=∠A+∠D﹣180°,
由(2)可知:∠F=2∠P=2n°,
∴∠A+∠D=180°+2n°.
(Ⅱ)如图③,延长AB交DC的延长线于F.
∵∠F=180°﹣∠A﹣∠D,∠P∠F,
∴∠P(180°﹣∠A﹣∠D)=90°(∠A+∠D).
∴∠A+∠D=180°﹣2n°
综上所述:∠A+∠D=180°+2n°或180°﹣2n°.
【变式8-2】(2020秋 平舆县期中)已知:如图,∠MON=90°,点A、B分别在射线OM、ON上移动(不与点O重合),AC平分∠MAB,AC的反向延长线与∠ABO的平分线相交于点D.
(1)当∠ABO=70°时、∠D的度数是多少?
(2)随着点A、B的移动,试问∠D的大小是否变化?请说出你的理由.
【解题思路】(1)利用三角形的外角性质可求出∠MAB的度数,由AC平分∠MAB,BD平分∠ABO,利用角平分线的定义可求出∠CAB和∠ABD的度数,再利用三角形的外角性质可求出∠D的度数;
(2)利用三角形的外角性质及角平分线的定义可用∠ABO表示出∠CAB和∠ABD的度数,再利用三角形的外角性质可求出∠D的度数为固定值,进而可得出∠D的大小不发生变化.
【解答过程】解:(1)∵∠MON=90°,∠ABO=70°,
∴∠MAB=∠AOB+∠ABO=90°+70°=160°.
∵AC平分∠MAB,
∴∠CAB∠MAB=80°.
∵BD平分∠ABO,
∴∠ABD∠ABO=35°.
又∵∠CAB=∠ABD+∠D,
∴∠D=∠CAB﹣∠ABD=80°﹣35°=45°.
(2)∠D的大小不变,理由如下:
∵∠MAB=∠AOB+∠ABO=90°+∠ABO,AC平分∠MAB,
∴∠CAB∠MAB=45°∠ABO.
∵BD平分∠ABO,
∴∠ABD∠ABO.
又∵∠CAB=∠ABD+∠D,
∴∠D=∠CAB﹣∠ABD=45°∠ABO∠ABO=45°,
∴∠D的大小不发生变化.
【变式8-3】(2020春 惠安县期末)在△ABC中,∠ACB的平分线CD与外角∠EAC的平分线AF所在的直线交于点D.
(1)如图1,若∠B=60°,求∠D的度数;
(2)如图2,把△ACD沿AC翻折,点D落在D′处.
①当AD′⊥AD时,求∠BAC的度数;
②试确定∠DAD′与∠BAC的数量关系,并说明理由.
【解题思路】(1)利用角平分线的定义和三角形的外角的性质进行代换可以得出∠B=2∠D,已知∠B=60°,可求∠D的度数;
(2)①根据折叠,可得等角,再利用特殊角,和周角的意义可以计算出∠DAC的度数,再利用平角的意义,可求出∠CAF,进而得出∠BAC的度数;
②设∠DAD′为任意角度,通过折叠、外角、角平分线,平角等代换,得出∠DAD′与∠BAC的数量关系,即∠DAD′与∠BAC互补的结论.
【解答过程】解:(1)如图1,
∵CD平分∠ACB,
∴∠ACD=∠DCB∠ACB,
∵AF是外角∠EAC的平分线,
∴∠CAF=∠FAE∠CAE,
又∵∠CAF=∠D+∠ACD,
∠CAE=∠B+∠ACB,
∴∠D∠B=30°;
(2)如图2,由折叠得:∠DAC=∠D′AC,
①当AD′⊥AD时,即:∠DAD′=90°,
∴∠DAC=∠D′AC=135°,
∴∠CAF=180°﹣135°=45°=∠FAE,
∴∠BAC=180°﹣45°﹣45°=90°,
答:当AD′⊥AD时,∠BAC=90°.
②设∠DAD′=α,则∠DAC=∠D′AC(360°﹣α)=180°α,
∴∠CAF=180°﹣∠DAC=180°﹣(180°α)α,
∴∠CAE=2∠CAF=α,
∴∠BAC=180°﹣α,
即:∠BAC+∠DAD′=180°,
答:∠DAD′与∠BAC的数量关系是:∠BAC+∠DAD′=180°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
