浙教版八年级上专题1.4 全等三角形的证明及计算大题专项训练(含解析)
文档属性
| 名称 | 浙教版八年级上专题1.4 全等三角形的证明及计算大题专项训练(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-19 17:31:38 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
全等三角形的证明及计算大题专项训练(30道)
1.(2021春 道里区期末)如图,点A,C在EF上,AD∥BC,DE∥BF,AE=CF.
(1)求证:△ADE≌△CBF;
(2)直接写出图中所有相等的线段(AE=CF除外).
2.(2021春 宁德期末)如图,AB,CD交于点O,AC=DB,∠ACD=∠DBA.
(1)说明△AOC≌△DOB的理由;
(2)若∠ACD=94°,∠CAO=28°,求∠OCB的度数.
3.(2021春 沙坪坝区校级期末)如图,在△ABC中,AC=BC,点D在AB边上,点E在BC边上,连接CD,DE.已知∠ACD=∠BDE,CD=DE.
(1)猜想AC与BD的数量关系,并证明你的猜想;
(2)若AD=3,BD=5,求CE的长.
4.(2021春 渝中区校级期末)如图,点E在△ABC的边AC上,且∠ABE=∠C,AF平分∠BAE交BE于F,FD∥BC交AC于点D.
(1)求证:△ABF≌△ADF;
(2)若BE=7,AB=8,AE=5,求△EFD的周长.
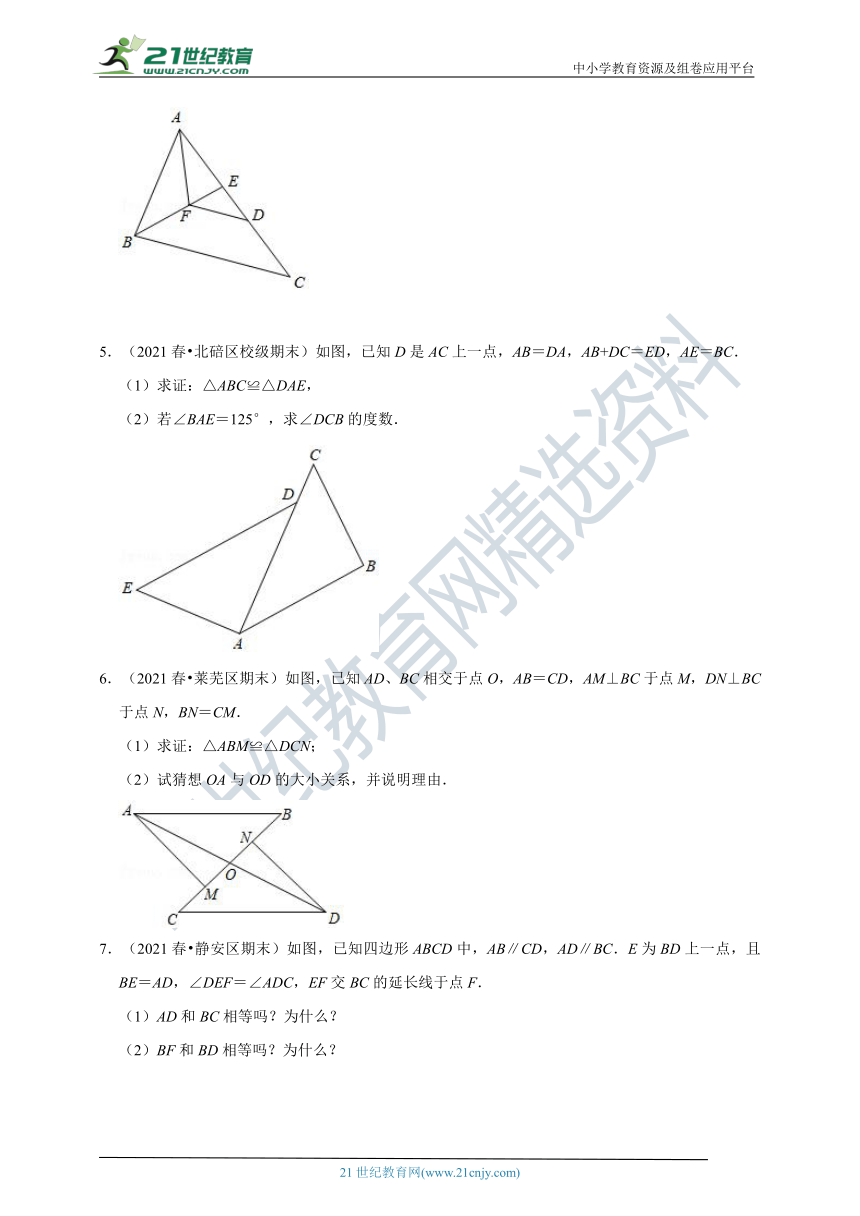
5.(2021春 北碚区校级期末)如图,已知D是AC上一点,AB=DA,AB+DC=ED,AE=BC.
(1)求证:△ABC≌△DAE,
(2)若∠BAE=125°,求∠DCB的度数.
6.(2021春 莱芜区期末)如图,已知AD、BC相交于点O,AB=CD,AM⊥BC于点M,DN⊥BC于点N,BN=CM.
(1)求证:△ABM≌△DCN;
(2)试猜想OA与OD的大小关系,并说明理由.
7.(2021春 静安区期末)如图,已知四边形ABCD中,AB∥CD,AD∥BC.E为BD上一点,且BE=AD,∠DEF=∠ADC,EF交BC的延长线于点F.
(1)AD和BC相等吗?为什么?
(2)BF和BD相等吗?为什么?
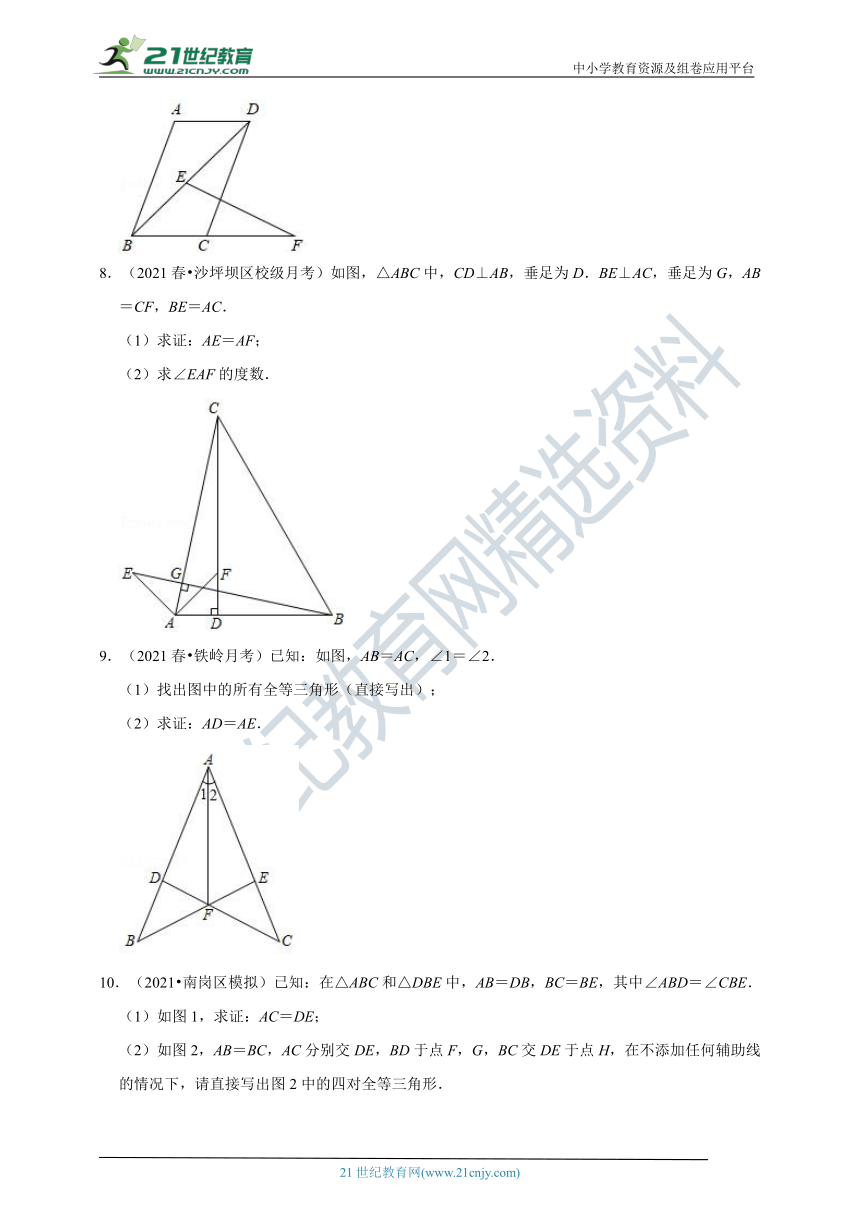
8.(2021春 沙坪坝区校级月考)如图,△ABC中,CD⊥AB,垂足为D.BE⊥AC,垂足为G,AB=CF,BE=AC.
(1)求证:AE=AF;
(2)求∠EAF的度数.
9.(2021春 铁岭月考)已知:如图,AB=AC,∠1=∠2.
(1)找出图中的所有全等三角形(直接写出);
(2)求证:AD=AE.
10.(2021 南岗区模拟)已知:在△ABC和△DBE中,AB=DB,BC=BE,其中∠ABD=∠CBE.
(1)如图1,求证:AC=DE;
(2)如图2,AB=BC,AC分别交DE,BD于点F,G,BC交DE于点H,在不添加任何辅助线的情况下,请直接写出图2中的四对全等三角形.
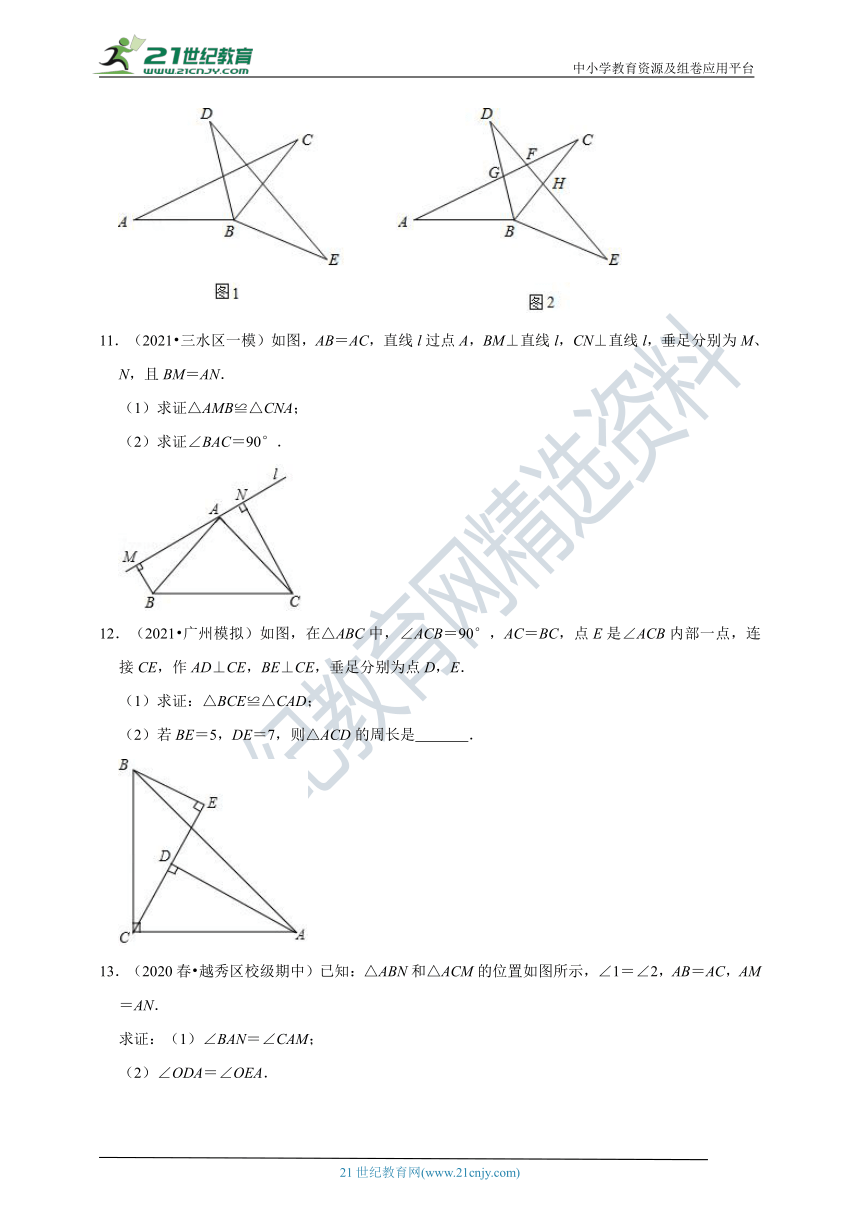
11.(2021 三水区一模)如图,AB=AC,直线l过点A,BM⊥直线l,CN⊥直线l,垂足分别为M、N,且BM=AN.
(1)求证△AMB≌△CNA;
(2)求证∠BAC=90°.
12.(2021 广州模拟)如图,在△ABC中,∠ACB=90°,AC=BC,点E是∠ACB内部一点,连接CE,作AD⊥CE,BE⊥CE,垂足分别为点D,E.
(1)求证:△BCE≌△CAD;
(2)若BE=5,DE=7,则△ACD的周长是 .
13.(2020春 越秀区校级期中)已知:△ABN和△ACM的位置如图所示,∠1=∠2,AB=AC,AM=AN.
求证:(1)∠BAN=∠CAM;
(2)∠ODA=∠OEA.
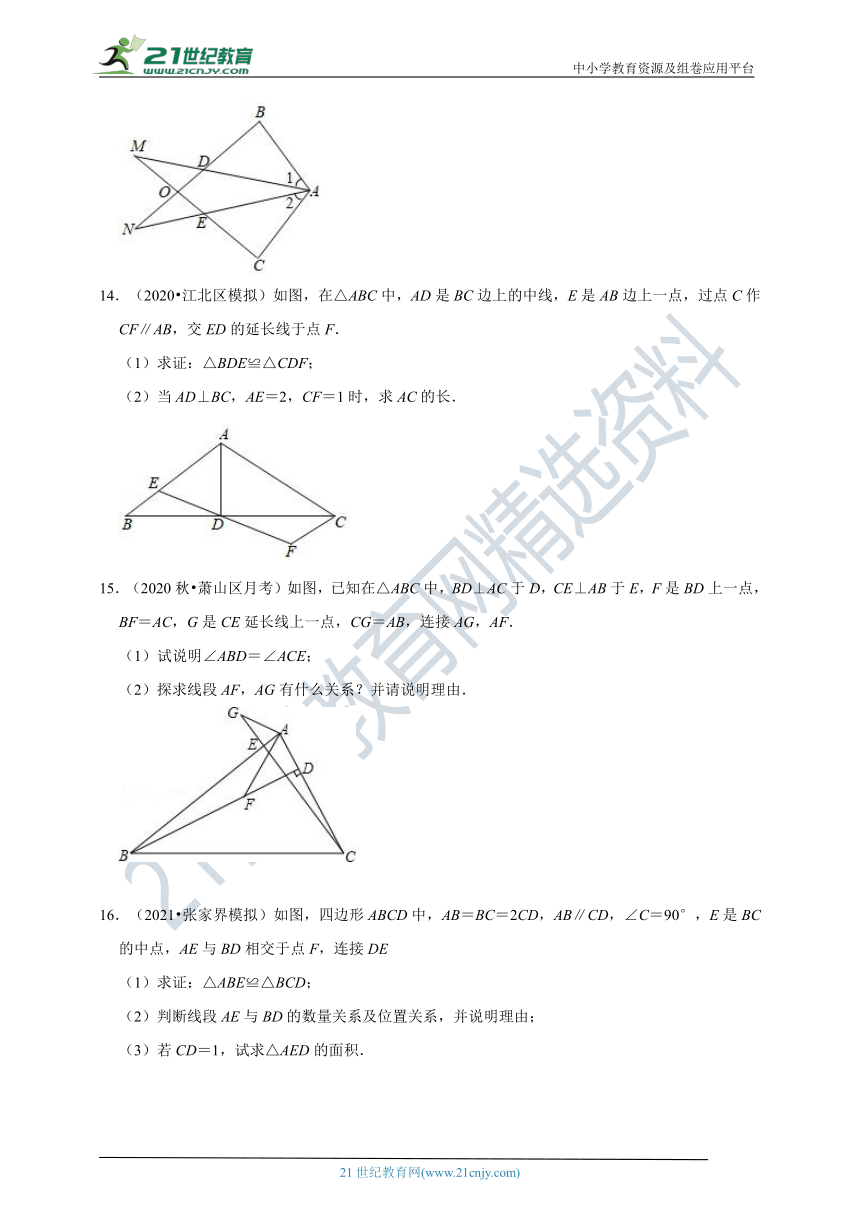
14.(2020 江北区模拟)如图,在△ABC中,AD是BC边上的中线,E是AB边上一点,过点C作CF∥AB,交ED的延长线于点F.
(1)求证:△BDE≌△CDF;
(2)当AD⊥BC,AE=2,CF=1时,求AC的长.
15.(2020秋 萧山区月考)如图,已知在△ABC中,BD⊥AC于D,CE⊥AB于E,F是BD上一点,BF=AC,G是CE延长线上一点,CG=AB,连接AG,AF.
(1)试说明∠ABD=∠ACE;
(2)探求线段AF,AG有什么关系?并请说明理由.
16.(2021 张家界模拟)如图,四边形ABCD中,AB=BC=2CD,AB∥CD,∠C=90°,E是BC的中点,AE与BD相交于点F,连接DE
(1)求证:△ABE≌△BCD;
(2)判断线段AE与BD的数量关系及位置关系,并说明理由;
(3)若CD=1,试求△AED的面积.
17.(2020秋 台江区校级期中)如图,A,B,C三点共线,D,C,E三点共线,∠A=∠DBC,EF⊥AC于点F,AE=BD.
(1)求证:C是DE的中点;
(2)求证:AB=2CF.
18.(2021春 铁岭月考)如图,△AOC和△BOD中,OA=OC,OB=OD,∠AOC=∠BOD=α(0<α<90°),AD与BC交于点P.
(1)求证:△AOD≌△COB;
(2)求∠APC(用含α的式子表示);
(3)过点O分别作OM⊥AD,ON⊥BC,垂足分别为点M、N,请直接写出OM和ON的数量关系.
19.(2020秋 花都区月考)如图所示,BD、CE是△ABC的高,点P在BD的延长线上,CA=BP,点Q在CE上,QC=AB.
(1)探究PA与AQ之间的关系;
(2)若把(1)中的△ABC改为钝角三角形,AC>AB,∠A是钝角,其他条件不变,上述结论是否成立?画出图形并证明你的结论.
20.(2020春 萍乡期末)在△ABC中,AB=AC,D是直线BC上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE,设∠BAC=∠1,∠DCE=∠2.
(1)如图①,当点D在线段BC上移动时,试说明:∠1+∠2=180°;
(2)如图②,当点D在线段BC的延长线上移动时,请猜测∠1与∠2有怎样的数量关系?并说明理由.
21.(2020春 揭阳期末)已知△ABC,点D、F分别为线段AC、AB上两点,连接BD、CF交于点E.
(1)若BD⊥AC,CF⊥AB,如图1所示,试说明∠BAC+∠BEC=180°;
(2)若BD平分∠ABC,CF平分∠ACB,如图2所示,试说明此时∠BAC与∠BEC的数量关系;
(3)在(2)的条件下,若∠BAC=60°,试说明:EF=ED.
22.(2020秋 淇滨区校级期中)(1)如图1所示,△ACB和△ECD都是等腰三角形,A、C、D三点在同一直线上,连接BD、AE,并延长AE交BD于点F,试判断AE与BD的数量关系及位置关系,并证明你的结论.
(2)若△ECD绕顶点C顺时针转任意角度后得到图2,图1中的结论是否仍然成立?请说明理由.
23.(2020秋 蒙阴县期中)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.
(1)当直线MN绕着点C旋转到如图1所示的位置时,
求证:①△ADC≌△CEB;
②DE=AD+BE;
(2)当直线MN绕着点C旋转到如图2所示的位置时,
①找出图中一对全等三角形;
②DE、AD、BE之间有怎样的数量关系,并加以证明.
24.(2020秋 环翠区期末)(1)如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,若∠EAF∠BAD,可求得EF、BE、FD之间的数量关系为 .(只思考解题思路,完成填空即可,不必书写证明过程)
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,若∠EAF∠BAD,判断EF、BE、FD之间的数量关系还成立吗,若成立,请完成证明,若不成立,请说明理由.【可借鉴第(1)问的解题经验】
25.(2021春 和平区期末)如图,在△ABC中,AC=BC,点D在边AB上,AB=4BD,连接CD,点E,F在线段CD上,连接BF,AE,∠BFC=∠AEC=180°﹣∠ACB.
(1)①∠FBC与∠ECA相等吗?说明你的理由;
②△FBC与△ECA全等吗?说明你的理由;
(2)若AE=11,EF=8,则请直接写出BF的长为 ;
(3)若△ACE与△BDF的面积之和为12,则△ABC的面积为 .
26.(2020 岱岳区一模)已知∠ABC=90°,点D是直线AB边上的点,AD=BC.
(1)如图1,点D在线段AB上,过点A作AF⊥AB,且AF=BD,连接DC、DF、CF,试判断△CDF的形状并说明理由;
(2)如图2,点D在线段AB的延长线上,点F在点A的左侧,其他条件不变,以上结论是否仍然成立?请说明理由.
27.如图(1),线段AD∥BC,连接AB、CD,取CD中点E,连接AE,AE平分∠BAD.
(1)线段AB与AD、BC之间存在怎样的等量关系?请说明理由.
(2)如果点C在AB的左侧,其他条件不变,如图(2)所示,那么(1)中的结论还成立吗?如果成立,请说明理由;如果不成立,请写出新的结论,并说明理由.
28.(2021春 章丘区期末)如图,CD是经过∠BCA顶点C的一条直线,CA=CB,E、F分别是直线CD上两点,且∠BEC=∠CFA=α.
(1)若直线CD经过∠BCA的内部,且E、F在射线CD上.
①如图1,若∠BCA=90°,α=90°,则BE CF;
②如图2,若0°<∠BCA<180°,请添加一个关于α与∠BCA关系的条件 ,使①中的结论们然成立,并说明明理由;
(2)如图3,若线CD经过∠BCA的外部,a=∠BCA,请提出关于EF,BE,AF三条线段数量关系的合理猜想,并简述理由.
29.(2020春 南岸区期末)在∠MAN内有一点D,过点D分别作DB⊥AM,DC⊥AN,垂足分别为B,C.且BD=CD,点E,F分别在边AM和AN上.
(1)如图1,若∠BED=∠CFD,请说明DE=DF;
(2)如图2,若∠BDC=120°,∠EDF=60°,猜想EF,BE,CF具有的数量关系,并说明你的结论成立的理由.
30.(2021春 揭东区期末)已知点C为线段AB上一点,分别以AC、BC为边在线段AB同侧作△ACD和△BCE,且CA=CD,CB=CE,∠ACD=∠BCE,直线AE与BD交于点F.
(1)如图1,求证:△ACE≌△DCB.
(2)如图1,若∠ACD=60°,则∠AFB= ;如图2,若∠ACD=90°,则∠AFB= ;
(3)如图3,若∠ACD=β,则∠AFB= (用含β的式子表示)并说明理由.
全等三角形的证明及计算大题专项训练(30道)
1.(2021春 道里区期末)如图,点A,C在EF上,AD∥BC,DE∥BF,AE=CF.
(1)求证:△ADE≌△CBF;
(2)直接写出图中所有相等的线段(AE=CF除外).
【解题思路】(1)利用ASA证明△ADE≌△CBF即可;
(2)根据△ADE≌△CBF即可得图中所有相等的线段.
【解答过程】(1)证明:∵AD∥BC
∴∠DAC=∠BCA,
又∵∠DAC+∠EAD=180°,∠BCA+∠FCB=180°,
∴∠EAD=∠FCB,
∵DE∥BF,
∴∠E=∠F,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(ASA),
(2)∵△ADE≌△CBF,
∴ED=FB,DA=BC,EC=FA.
∵AD∥BC,
∴∠DAC=∠BCA,
在△ADC和△CBA中,
,
∴△ADC≌△CBA(SAS),
∴AB=CD;
∴图中所有相等的线段有:ED=FB,DA=BC,AB=CD,EC=FA.
2.(2021春 宁德期末)如图,AB,CD交于点O,AC=DB,∠ACD=∠DBA.
(1)说明△AOC≌△DOB的理由;
(2)若∠ACD=94°,∠CAO=28°,求∠OCB的度数.
【解题思路】(1)直接利用AAS即可证明△AOC≌△DOB;
(2)利用三角形外角的性质得到∠COB,再根据△AOC≌△DOB得到OC=OB,即可求得∠OCB.
【解答过程】解:(1)在△AOC和△DOB中,
,
∴△AOC≌△DOB(AAS);
(2)∵∠ACD=94°,∠CAO=28°,
∴∠COB=∠ACD+∠CAO=122°,
∵△AOC≌△DOB,
∴OC=OB,
∴∠OCB=(180°﹣122°)÷2=29°.
3.(2021春 沙坪坝区校级期末)如图,在△ABC中,AC=BC,点D在AB边上,点E在BC边上,连接CD,DE.已知∠ACD=∠BDE,CD=DE.
(1)猜想AC与BD的数量关系,并证明你的猜想;
(2)若AD=3,BD=5,求CE的长.
【解题思路】(1)利用AAS证明△ADC≌△BED,即可得结论;
(2)结合△ADC≌△BED,可得AC=BD=5,BE=AD=3,进而可得CE的长.
【解答过程】解:(1)AC=BD,理由如下:
∵AC=BC,
∴∠A=∠B,
在△ADC和△BED中,
,
∴△ADC≌△BED(AAS),
∴AC=BD;
(2)由(1)知:△ADC≌△BED,
∴AC=BD=5,BE=AD=3,
∴BC=AC=5,
∴CE=BC﹣BE=2.
4.(2021春 渝中区校级期末)如图,点E在△ABC的边AC上,且∠ABE=∠C,AF平分∠BAE交BE于F,FD∥BC交AC于点D.
(1)求证:△ABF≌△ADF;
(2)若BE=7,AB=8,AE=5,求△EFD的周长.
【解题思路】(1)根据平行线的性质得到∠ADF=∠C,等量代换得到∠ABF=∠ADF,由角平分线的定义得到∠BAF=∠CAF,根据全等三角形的判定定理即可得到结论;
(2)根据全等三角形的性质得到AD=AB=8,BF=DF,由线段的和差得到DE=AD=AE=8﹣5=3,根据三角形的周长公式即可得到结论.
【解答过程】解:(1)∵FD∥BC,
∴∠ADF=∠C,
∵∠ABF=∠C,
∴∠ABF=∠ADF,
∵AF平分∠BAE,
∴∠BAF=∠CAF,
在△ABF和△ADF中,
,
∴△ABF≌△ADF(AAS);
(2)∵△ABF≌△ADF,
∴AD=AB=8,BF=DF,
∵AE=5,
∴DE=AD﹣AE=8﹣5=3,
∴△EFD的周长=EF+DF+DE=EF+BF+DE=BE+DE=7+3=10.
5.(2021春 北碚区校级期末)如图,已知D是AC上一点,AB=DA,AB+DC=ED,AE=BC.
(1)求证:△ABC≌△DAE,
(2)若∠BAE=125°,求∠DCB的度数.
【解题思路】(1)根据SSS证明三角形全等即可.
(2)利用全等三角形的性质以及三角形内角和定理求解即可.
【解答过程】(1)证明:∵DE=AB+DC,AB=AD,
∴DE=AD+DC=AC,
在△ABC和△DAE中,
,
∴△ABC≌△DAE(SSS).
(2)解:∵△ABC≌△DAE,
∴∠EAD=∠B,
∴∠B+∠BAC=∠EAD+∠BAC=∠EAB=125°,
∴∠DCB=180°﹣(∠B+∠BAC)=180°﹣125°=55°.
6.(2021春 莱芜区期末)如图,已知AD、BC相交于点O,AB=CD,AM⊥BC于点M,DN⊥BC于点N,BN=CM.
(1)求证:△ABM≌△DCN;
(2)试猜想OA与OD的大小关系,并说明理由.
【解题思路】(1)根据HL可证明:△ABM≌△DCN;
(2)根据AAS证明△AMO≌△DNO可得结论.
【解答过程】(1)证明:∵BN=CM,
∴BN+MN=MN+CM,
即CN=BM,
∵AM⊥BC于点M,DN⊥BC于点N,
∴∠AMB=∠DNC=90°,
在Rt△ABM和Rt△DCN中,
,
∴Rt△ABM≌Rt△DCN(HL);
(2)解:OA=OD,理由如下:
∵Rt△ABM≌Rt△DCN,
∴AM=DN,
在△AMO和△DNO中,
,
∴△AMO≌△DNO(AAS),
∴OA=OD.
7.(2021春 静安区期末)如图,已知四边形ABCD中,AB∥CD,AD∥BC.E为BD上一点,且BE=AD,∠DEF=∠ADC,EF交BC的延长线于点F.
(1)AD和BC相等吗?为什么?
(2)BF和BD相等吗?为什么?
【解题思路】(1)根据平行线的性质和全等三角形的判定和性质得出△ABD与△CDB全等,进而利用全等三角形的性质解答即可;
(2)根据平行线的性质和全等三角形的判定和性质得出△EFB与△CDB全等,进而解答即可.
【解答过程】解:(1)AD=CB,理由如下:
∵AD∥BC,
∴∠ABD=∠CDB,
同理可得,∠ADB=∠CBD,
在△ABD与△CDB中,
,
∴△ABD≌△CDB(ASA),
∴AD=CB;
(2)BF=BD,理由如下:
∵AD=CB,BE=AD,
∴BC=BE,
∵∠DEF=∠ADC,
∴∠DEF﹣∠DBF=∠ADC﹣∠ADB,
即∠EFB=∠CDB,
在△EFB与△CDB中,
,
∴△EFB≌△CDB(ASA),
∴FB=DB.
8.(2021春 沙坪坝区校级月考)如图,△ABC中,CD⊥AB,垂足为D.BE⊥AC,垂足为G,AB=CF,BE=AC.
(1)求证:AE=AF;
(2)求∠EAF的度数.
【解题思路】(1)利用SAS证明△AEB≌△FAC可证明结论;
(2)由全等三角形的性质可得∠E=∠CAF,由余角的定义可求得∠EAF的度数.
【解答过程】(1)证明:∵CD⊥AB,BE⊥AC,
∴∠CAD+∠ACD=∠CAD+∠EBA=90°,
∴∠ACD=∠EBA,
在△AEB和△FAC中,
,
∴△AEB≌△FAC(SAS),
∴AE=FA;
(2)解:∵△AEB≌△FAC,
∴∠E=∠CAF,
∵∠E+∠EAG=90°,
∴∠CAF+∠EAG=90°,
即∠EAF=90°.
9.(2021春 铁岭月考)已知:如图,AB=AC,∠1=∠2.
(1)找出图中的所有全等三角形(直接写出);
(2)求证:AD=AE.
【解题思路】(1)直接根据全等三角形的判定可得答案;
(2)先根据SAS证得△ABF≌△ACF,再根据ASA证得△BDF≌△CEF,然后根据全等三角形的性质可得结论.
【解答过程】解:(1)△ABF≌△ACF,△BDF≌△CEF,△ADF≌△AEF,△ADC≌△AEB;
(2)证明:在△ABF和△ACF中,
,
∴△ABF≌△ACF(SAS),
∴∠B=∠C,BF=CF.
在△BDF和△CEF中,
,
∴△BDF≌△CEF(ASA),
∴BD=CE,
∴AB﹣BD=AC﹣CE,
∴AD=AE.
10.(2021 南岗区模拟)已知:在△ABC和△DBE中,AB=DB,BC=BE,其中∠ABD=∠CBE.
(1)如图1,求证:AC=DE;
(2)如图2,AB=BC,AC分别交DE,BD于点F,G,BC交DE于点H,在不添加任何辅助线的情况下,请直接写出图2中的四对全等三角形.
【解题思路】(1)根据SAS证明△ABC与△DBE全等,利用全等三角形的性质解答即可.
(2)根据全等三角形的判定解答即可.
【解答过程】证明:(1)∵∠ABD=∠CBE,
∴∠ABD+∠DBC=∠CBE+∠DBC,
即∠ABC=∠DBE,
在△ABC与△DBE中,
,
∴△ABC≌△DBE(SAS),
∴AC=DE;
(2)由(1)得△ABC≌△DBE,
∴∠A=∠D,∠C=∠E,AB=DB,BC=BE,
∴AB=BE,
∵AB=BC,
∴∠A=∠C,
∴∠A=∠E,
在△ABG与△EBH中,
,
∴△ABG≌△EBH(ASA),
∴BG=BH,
在△DBH与△CBG中,
,
∴△DBH≌△CBG(SAS),
∴∠D=∠C,
∵DB=CB,BG=BH,
∴DG=CH,
在△DFG与△CFH中,
,
∴△DFG≌△CFH(AAS).
11.(2021 三水区一模)如图,AB=AC,直线l过点A,BM⊥直线l,CN⊥直线l,垂足分别为M、N,且BM=AN.
(1)求证△AMB≌△CNA;
(2)求证∠BAC=90°.
【解题思路】(1)由HL证明△AMB≌△CNA即可;
(2)先由全等三角形的性质得∠BAM=∠ACN,再由∠CAN+∠ACN=90°,得∠CAN+∠BAM=90°,即可得出结论.
【解答过程】证明:(1)∵BM⊥直线l,CN⊥直线l,
∴∠AMB=∠CNA=90°,
在Rt△AMB和Rt△CNA中,
,
∴Rt△AMB≌Rt△CNA(HL);
(2)由(1)得:Rt△AMB≌Rt△CNA,
∴∠BAM=∠ACN,
∵∠CAN+∠ACN=90°,
∴∠CAN+∠BAM=90°,
∴∠BAC=180°﹣90°=90°.
12.(2021 广州模拟)如图,在△ABC中,∠ACB=90°,AC=BC,点E是∠ACB内部一点,连接CE,作AD⊥CE,BE⊥CE,垂足分别为点D,E.
(1)求证:△BCE≌△CAD;
(2)若BE=5,DE=7,则△ACD的周长是 30 .
【解题思路】(1)根据条件可以得出∠E=∠ADC=90°,进而得出△CEB≌△ADC;
(2)利用(1)中结论,根据全等三角形的性质即可解决问题;
【解答过程】(1)证明:∵BE⊥CE,AD⊥CE,
∴∠E=∠ADC=90°,
∴∠EBC+∠BCE=90°.
∵∠BCE+∠ACD=90°,
∴∠EBC=∠DCA.
在△BCE和△CAD中,
,
∴△BCE≌△CAD(AAS);
(2)解:∵:△BCE≌△CAD,BE=5,DE=7,
∴BE=DC=5,CE=AD=CD+DE=5+7=12.
∴由勾股定理得:AC=13,
∴△ACD的周长为:5+12+13=30,
故答案为:30.
13.(2020春 越秀区校级期中)已知:△ABN和△ACM的位置如图所示,∠1=∠2,AB=AC,AM=AN.
求证:(1)∠BAN=∠CAM;
(2)∠ODA=∠OEA.
【解题思路】(1)由∠1=∠2,则∠1+∠MAN=∠2+∠MAN,即∠BAN=∠CAM;
(2)先证△ACM≌△ABN(SAS),得∠M=∠N,再证△ADN≌△AEM(ASA),即可得出结论.
【解答过程】证明:(1)∵∠1=∠2,
∴∠1+∠MAN=∠2+∠MAN,
即∠BAN=∠CAM;
(2)在△ACM和△ABN中,
,
∴△ACM≌△ABN(SAS),
∴∠M=∠N,
在△ADN和△AEM中,
,
∴△ADN≌△AEM(ASA),
∴∠NDA=∠MEA,
即∠ODA=∠OEA.
14.(2020 江北区模拟)如图,在△ABC中,AD是BC边上的中线,E是AB边上一点,过点C作CF∥AB,交ED的延长线于点F.
(1)求证:△BDE≌△CDF;
(2)当AD⊥BC,AE=2,CF=1时,求AC的长.
【解题思路】(1)根据平行线的性质得到∠B=∠FCD,∠BED=∠F,由AD是BC边上的中线,得到BD=CD,于是得到结论;
(2)根据全等三角形的性质得到BE=CF=1,求得AB=AE+BE=3,于是得到结论.
【解答过程】证明:∵CF∥AB,
∴∠B=∠FCD,∠BED=∠F,
∵AD是BC边上的中线,
∴BD=CD,在△BDE和△CDF中,
,
∴△BDE≌△CDF(AAS);
(2)∵△BDE≌△CDF,
∴BE=CF=1,
∴AB=AE+BE=2+1=3,
∵AD⊥BC,BD=CD,
∴AC=AB=3.
15.(2020秋 萧山区月考)如图,已知在△ABC中,BD⊥AC于D,CE⊥AB于E,F是BD上一点,BF=AC,G是CE延长线上一点,CG=AB,连接AG,AF.
(1)试说明∠ABD=∠ACE;
(2)探求线段AF,AG有什么关系?并请说明理由.
【解题思路】(1)根据的等角的余角相等,即可证明∠ACG=∠ABF;
(2)根据SAS推出△ABF≌△GCA即可解决问题;
【解答过程】(1)证明:∵BD、CE是△ABC的高,
∴∠ADB=∠AEC=90°,
∴∠ABF+∠BAD=90°,∠GCA+∠BAD=90°,
∴∠ABF=∠GCA,
(2)结论:AF=AG,AF⊥AG.理由如下:
在△ABF和△GCA中,
,
∴△ABF≌△GCA(SAS),
∴AF=AG,∠GAC=∠AFB,
∵∠AFB=∠ADB+∠FAD,∠GAC=∠GAF+∠FAD,
∴∠GAF=∠ADF,
∵∠ADF=90°,
∴∠GAF=90°,
∴AG⊥AF,AG=AF.
16.(2021 张家界模拟)如图,四边形ABCD中,AB=BC=2CD,AB∥CD,∠C=90°,E是BC的中点,AE与BD相交于点F,连接DE
(1)求证:△ABE≌△BCD;
(2)判断线段AE与BD的数量关系及位置关系,并说明理由;
(3)若CD=1,试求△AED的面积.
【解题思路】(1)由平行线的性质得出∠ABE+∠C=180°,得出∠ABE=90°=∠C,再证出BE=CD,由SAS证明△ABE≌△BCD即可;
(2)由全等三角形的性质得出AE=BD,证出∠ABF+∠BAE=90°,得出∠AFB=90°,即可得出结论;
(3)由全等三角形的性质得出BE=CD=1,求出CE=BC﹣BE=1,得出CE=CD,△AED的面积=梯形ABCD的面积﹣△ABE的面积﹣△CDE的面积,即可得出答案.
【解答过程】(1)证明:∵AB∥CD,
∴∠ABE+∠C=180°,
∵∠C=90°,
∴∠ABE=90°=∠C,
∵E是BC的中点,
∴BC=2BE,
∵BC=2CD,
∴BE=CD,
在△ABE和△BCD中,,
∴△ABE≌△BCD(SAS);
(2)解:AE=BD,AE⊥BD,理由如下:
由(1)得:△ABE≌△BCD,
∴AE=BD,
∵∠BAE=∠CBD,∠ABF+∠CBD=90°,
∴∠ABF+∠BAE=90°,
∴∠AFB=90°,
∴AE⊥BD;
(3)解:∵△ABE≌△BCD,
∴BE=CD=1,
∵AB=BC=2CD=2,
∴CE=BC﹣BE=1,
∴CE=CD,
∴△AED的面积=梯形ABCD的面积﹣△ABE的面积﹣△CDE的面积(1+2)×22×11×1.
17.(2020秋 台江区校级期中)如图,A,B,C三点共线,D,C,E三点共线,∠A=∠DBC,EF⊥AC于点F,AE=BD.
(1)求证:C是DE的中点;
(2)求证:AB=2CF.
【解题思路】(1)过D作DH⊥AC的延长线与H,根据全等三角形的判定证得△AEF≌△BDH,得到EF=DH,再证得△EFC≌△DHC得到CE=CD,即可证得即可证得结论;
(2)由(1)得,△AEF≌△BDH,△EFC≌△DHC,根据全等三角形的性质得到AF=BH,CF=CH,再根据线段的和差即可证得结论.
【解答过程】证明:(1)过D作DH⊥AC的延长线与H,
∴∠EFC=∠DHC=90°,
在△AEF和△BDH中,
,
∴△AEF≌△BDH(AAS),
∴EF=DH,
在△EFC和△DHC中,
,
∴△EFC≌△DHC(AAS),
∴CE=CD,
∴C是DE的中点;
(2)由(1)得,△AEF≌△BDH,△EFC≌△DHC,
∴AF=BH,CF=CH,
∴AB+BF=BF+FH,FH=2FC,
∴AB=FH,
∴AB=2CF.
18.(2021春 铁岭月考)如图,△AOC和△BOD中,OA=OC,OB=OD,∠AOC=∠BOD=α(0<α<90°),AD与BC交于点P.
(1)求证:△AOD≌△COB;
(2)求∠APC(用含α的式子表示);
(3)过点O分别作OM⊥AD,ON⊥BC,垂足分别为点M、N,请直接写出OM和ON的数量关系.
【解题思路】(1)由∠AOC=∠BOD,可得∠AOD=∠COB,然后根据SAS可得结论;
(2)根据全等三角形的性质得∠OAD=∠OCB,再根据三角形外角性质可得答案;
(3)根据全等三角形的性质得∠MAO=∠NCO,由垂直定义得∠AMO=∠CNO,再根据全等三角形的判定与性质可得结论.
【解答过程】解:(1)∵∠AOC=∠BOD,
∴∠AOC+∠COD=∠BOD+∠COD,
∴∠AOD=∠COB,
在△AOD和△COB中,
,
∴△AOD≌△COB(SAS);
(2)由(1)可知△AOD≌△COB,
∴∠OAD=∠OCB,
令AD与OC交于点E,
则∠AEC=∠OAD+∠AOC=∠OCB+∠APC,
∴∠AOC=∠APC,
∵∠AOC=α,
∴∠APC=α;
(3)∵△AOD≌△COB,
∴∠PAP=∠BCO,即∠MAO=∠NCO,
∵OM⊥AD,ON⊥BC,
∴∠AMO=∠CNO=90°,
在△AOM和△CON中,
,
∴△AOM≌△CON(AAS),
∴OM=ON.
19.(2020秋 花都区月考)如图所示,BD、CE是△ABC的高,点P在BD的延长线上,CA=BP,点Q在CE上,QC=AB.
(1)探究PA与AQ之间的关系;
(2)若把(1)中的△ABC改为钝角三角形,AC>AB,∠A是钝角,其他条件不变,上述结论是否成立?画出图形并证明你的结论.
【解题思路】(1)由条件可得出∠1=∠2,可证得△APB≌△QAC,可得结论;
(2)根据题意画出图形,结合(1)可证得△APB≌△QAC,可得结论.
【解答过程】(1)结论:AP=AQ,AP⊥AQ
证明:∵BD、CE是△ABC的高,
∴BD⊥AC,CE⊥AB,
∴∠1+∠CAB=90°,∠2+∠CAB=90°,
∴∠1=∠2,
在△QAC和△APB中,
,
∴△QAC≌△APB(SAS),
∴AQ=AP,∠QAC=∠P,
而∠DAP+∠P=90°,
∴∠DAP+∠QAC=90°,
即∠QAP=90°,
∴AQ⊥AP;
即AP=AQ,AP⊥AQ;
(2)上述结论成立,理由如下:
如图所示:
∵BD、CE是△ABC的高,
∴BD⊥AC,CE⊥AB,
∴∠1+∠CAE=90°,∠2+∠DAB=90°,
∵∠CAE=∠DAB,
∴∠1=∠2,
在△QAC和△APB中,
,
∴△QAC≌△APB(SAS),
∴AQ=AP,∠QAC=∠P,
∵∠PDA=90°,
∴∠P+∠PAD=90°,
∴∠QAC+∠PAD=90°,
∴∠QAP=90°,
∴AQ⊥AP,
即AP=AQ,AP⊥AQ.
20.(2020春 萍乡期末)在△ABC中,AB=AC,D是直线BC上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE,设∠BAC=∠1,∠DCE=∠2.
(1)如图①,当点D在线段BC上移动时,试说明:∠1+∠2=180°;
(2)如图②,当点D在线段BC的延长线上移动时,请猜测∠1与∠2有怎样的数量关系?并说明理由.
【解题思路】(1)由“SAS”可证△BAD≌△CAE,可得∠ACE=∠ABD,由三角形的内角和定理可得结论;
(2)由“SAS”可证△BAD≌△CAE,可得∠ACE=∠ABD,由三角形的内角和定理和平角的定义可得结论.
【解答过程】证明:(1)∵∠DAE=∠BAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△BAD≌△CAE(SAS),
∴∠ACE=∠ABD,
∵∠BAC+∠ABD+∠ACB=180°,
∴∠BAC+∠ACB+∠ACE=∠BAC+∠BCE=180°,
∴∠1+∠2=180°;
(2)∠1=∠2,
理由如下:∵∠DAE=∠BAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△BAD≌△CAE(SAS),
∴∠ACE=∠ABD,
∵∠BAC+∠ABD+∠ACB=180°,∠ACE+∠ACB+∠DCE=180°,
∴∠1=∠2.
21.(2020春 揭阳期末)已知△ABC,点D、F分别为线段AC、AB上两点,连接BD、CF交于点E.
(1)若BD⊥AC,CF⊥AB,如图1所示,试说明∠BAC+∠BEC=180°;
(2)若BD平分∠ABC,CF平分∠ACB,如图2所示,试说明此时∠BAC与∠BEC的数量关系;
(3)在(2)的条件下,若∠BAC=60°,试说明:EF=ED.
【解题思路】(1)根据余角的性质得到∠DEC=∠BAC,由于∠DEC+∠BEC=180°,即可得到结论;
(2)根据角平分线的性质得到∠EBCABC,∠ECBACB,于是得到结论;
(3)作∠BEC的平分线EM交BC于M,由∠BAC=60°,得到∠BEC=90°BAC=120°,求得∠FEB=∠DEC=60°,根据角平分线的性质得到∠BEM=60°,推出△FBE≌△EBM,根据全等三角形的性质得到EF=EM,同理DE=EM,即可得到结论.
【解答过程】解:(1)∵BD⊥AC,CF⊥AB,
∴∠DCE+∠DEC=∠DCE+∠FAC=90°,
∴∠DEC=∠BAC,∠DEC+∠BEC=180°,
∴∠BAC+∠BEC=180°;
(2)∵BD平分∠ABC,CF平分∠ACB,
∴∠EBCABC,∠ECBACB,∠BEC=180°﹣(∠EBC+∠ECB)=180°(∠ABC+∠ACB)=180°(180°﹣∠BAC)=90°∠BAC;
(3)作∠BEC的平分线EM交BC于M,
∵∠BAC=60°,
∴∠BEC=90°BAC=120°,
∴∠FEB=∠DEC=60°,
∵EM平分∠BEC,
∴∠BEM=60°,
在△FBE与△EBM中,
,
∴△FBE≌△EBM(ASA),
∴EF=EM,同理DE=EM,
∴EF=DE.
22.(2020秋 淇滨区校级期中)(1)如图1所示,△ACB和△ECD都是等腰三角形,A、C、D三点在同一直线上,连接BD、AE,并延长AE交BD于点F,试判断AE与BD的数量关系及位置关系,并证明你的结论.
(2)若△ECD绕顶点C顺时针转任意角度后得到图2,图1中的结论是否仍然成立?请说明理由.
【解题思路】(1)根据SAS推出△ACE≌△BCD,根据全等三角形的性质得出∠CAE=∠DBC,根据∠ACB=90°求出∠CAE+∠AEC=90°,求出∠DBC+∠BEF=90°,根据三角形内角和定理求出∠BFE=90°即可;
(2)根据SAS推出△ACE≌△BCD,根据全等三角形的性质得出∠CAE=∠DBC,根据∠ACB=90°求出∠CAE+∠AOC=90°,求出∠DBC+∠BOE=90°,根据三角形内角和定理求出∠BFO=90°即可.
【解答过程】(1)AE⊥BD.
证明:在△ACE和△BCD中
∴△ACE≌△BCD(SAS),
∴∠CAE=∠DBC,
∵∠ACB=90°,
∴∠CAE+∠AEC=90°,
∵∠CAE=∠DBC,∠AEC=∠BEF,
∴∠DBC+∠BEF=90°,
∴∠BFE=180°﹣90°=90°,
∴AE⊥BD;
(2)解:结论还成立,
理由是:∵∠ACB=∠ECD,
∴∠ACB+∠BCE=∠ECD+∠BCE,
即∠ACE=∠BCD,
在△ACE和△BCD中
∴△ACE≌△BCD(SAS),
∴∠CAE=∠DBC,
∵∠ACB=90°,
∴∠CAE+∠AOC=90°,
∵∠CAE=∠DBC,∠AOC=∠BOE,
∴∠DBC+∠BOE=90°,
∴∠BFO=180°﹣90°=90°,
∴AE⊥BD.
23.(2020秋 蒙阴县期中)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.
(1)当直线MN绕着点C旋转到如图1所示的位置时,
求证:①△ADC≌△CEB;
②DE=AD+BE;
(2)当直线MN绕着点C旋转到如图2所示的位置时,
①找出图中一对全等三角形;
②DE、AD、BE之间有怎样的数量关系,并加以证明.
【解题思路】(1)根据余角和补角的性质易证得∠DAC=∠ECB,已知∠ADC=∠CEB=90°,AC=CB,根据全等三角形的判定AAS即可证明△ADC≌△CEB,根据各边的相等关系即可得DE=AD+BE.
(2)同理可证得△ADC≌△CEB,再根据各边的相等关系可得DE=AD﹣BE.
【解答过程】(1)证明:∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90°,
∴∠DAC+∠ACD=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=180°﹣90°=90°,
∴∠DAC=∠ECB;
在△ADC和△CEB中,∠ADC=∠CEB,∠DAC=∠ECB,AC=CB,
∴△ADC≌△CEB(AAS)①,(7分)
∴DC=EB,AD=CE,
∴DE=AD+BE.(9分)
(2)解:同理可得△ADC≌△CEB①;(11分)
∴AD=CE,CD=BE,
∴DE=AD﹣BE②.(14分)
24.(2018秋 环翠区期末)(1)如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,若∠EAF∠BAD,可求得EF、BE、FD之间的数量关系为 BE+DF=EF .(只思考解题思路,完成填空即可,不必书写证明过程)
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,若∠EAF∠BAD,判断EF、BE、FD之间的数量关系还成立吗,若成立,请完成证明,若不成立,请说明理由.【可借鉴第(1)问的解题经验】
【解题思路】(1)线段EF、BE、FD之间的数量关系是BE+DF=EF.如图1中,延长CB至M,使BM=DF,连接AM,利用全等三角形的性质解决问题即可.
(2)结论:EF+DF=BE.如图2中,在BE上截取BM=DF,连接AM,证明△ABM≌△ADF(SAS),推出AM=AF,∠BAM=∠DAF,再证明△AEM≌△AEF(SAS),可得结论.
【解答过程】解:(1)线段EF、BE、FD之间的数量关系是BE+DF=EF.
如图1,延长CB至M,使BM=DF,连接AM,
∵∠ABC+∠D=180°,∠ABC+∠1=180°,
∴∠1=∠D,
在△ABM和△ADF中,
,
∴△ABM≌△ADF(SAS),
∴AM=AF,∠3=∠2,
∵∠EAF∠BAD,
∴∠4+∠4=∠EAF,
∴∠GAM=∠3+∠4=∠2+∠4=∠EAF,
在△MAE和△FAE中,
,
∴△MAE≌△FAE(SAS),
∴EF=EM,
∵EM=BM+BE=BE+DF,
∴EF=BE+FD;
故答案为:BE+DF=EF.
(2)结论:EF+DF=BE.
理由:在BE上截取BM=DF,连接AM,
∵∠B+∠ADC=180°,∠ADC+∠ADE=180°,
∴∠B=∠ADF,
在△ABM与△ADF中,
,
∴△ABM≌△ADF(SAS),
∴AM=AF,∠BAM=∠DAF,
∵,
∴∠EAF=∠EAM,
在△AEM与△AEF中,
,
∴△AEM≌△AEF(SAS),
∴EM=EF,
即BE﹣BM=EF,
即BE﹣DF=EF,
∴EF+DF=BE.
25.(2021春 和平区期末)如图,在△ABC中,AC=BC,点D在边AB上,AB=4BD,连接CD,点E,F在线段CD上,连接BF,AE,∠BFC=∠AEC=180°﹣∠ACB.
(1)①∠FBC与∠ECA相等吗?说明你的理由;
②△FBC与△ECA全等吗?说明你的理由;
(2)若AE=11,EF=8,则请直接写出BF的长为 3 ;
(3)若△ACE与△BDF的面积之和为12,则△ABC的面积为 48 .
【解题思路】(1)①连接BC,由已知及∠AEC=180°﹣∠AED,可得到∠ACB=∠AED.再证明∠CAE=∠BCF,由三角形内角和定理可得∠FBC=∠ECA;②利用“ASA”证明△FBC≌△ECA;
(2)由(1)中全等三角形的结论及已知可得到BF的长;
(3)由(1)中结论可得S△FBC=S△ECA,所以S△ECA+S△BDF=12=S△FBC+S△BDF=S△DBC,根据AB=4BD,可得到S△DBCS△ABC=12,从而可得△ABC的面积.
【解答过程】解:(1)①∠FBC=∠ECA,理由如下:
连接BC,如右图.
∵∠BFC=∠AEC=180°﹣∠ACB,且∠AEC=180°﹣∠AED,
∴∠ACB=∠AED.
由外角定理可得∠AED=∠ACD+∠CAE,
又∠ACB=∠ACD+∠BCF,
∴∠CAE=∠BCF,
由三角形内角和定理可得∠FBC=∠ECA.
②△FBC与△ECA全等,理由如下:
在△FBC和△ECA中,
,
∴△FBC≌△ECA(ASA).
(2)由(1)中②可知,FC=AE=11,BF=CE,
又EF=8,
∴CE=FC﹣EF=11﹣8=3,
∴BF=3,
故答案为:3.
(3)由(1)中结论可知S△FBC=S△ECA,
∴S△ECA+S△BDF=12=S△FBC+S△BDF=S△DBC,
又AB=4BD,
∴S△DBCS△ABC=12,
∴S△ABC=48.
故答案为:48.
26.(2020 岱岳区一模)已知∠ABC=90°,点D是直线AB边上的点,AD=BC.
(1)如图1,点D在线段AB上,过点A作AF⊥AB,且AF=BD,连接DC、DF、CF,试判断△CDF的形状并说明理由;
(2)如图2,点D在线段AB的延长线上,点F在点A的左侧,其他条件不变,以上结论是否仍然成立?请说明理由.
【解题思路】(1)利用SAS证明△FAD≌△DBC,再利用全等三角形的性质得出FD=DC,即可判断三角形的形状;
(2)利用SAS证明△FAD和△DBC全等,再利用全等三角形的性质得出FD=DC,∠FDC=90°,即可得出结论.
【解答过程】(1)△CDF是等腰直角三角形,
理由如下:
∵AF⊥AB,
∴∠A=90°,
在△FAD和△DBC中,
∵,
∴△FAD≌△DBC(SAS),
∴∠ADF=∠BCD,DF=DC,
∵∠BDC+∠BCD=90°,
∴∠ADF+∠CDB=90°,
∴∠FDC=180°﹣90°=90°,
又∵DF=DC,
∴△CDF是等腰直角三角形;
(2)仍然成立,
理由如下:
∵AF⊥AB,
∴∠A=90°,
在△FAD和△DBC中,
∵,
∴△FAD≌△DBC(SAS),
∴∠ADF=∠BCD,DF=DC,
∵∠BDC+∠BCD=90°,
∴∠ADF+∠BDC=90°,即∠FDC=90°,
又∵DF=DC,
∴△CDF是等腰直角三角形.
27.如图(1),线段AD∥BC,连接AB、CD,取CD中点E,连接AE,AE平分∠BAD.
(1)线段AB与AD、BC之间存在怎样的等量关系?请说明理由.
(2)如果点C在AB的左侧,其他条件不变,如图(2)所示,那么(1)中的结论还成立吗?如果成立,请说明理由;如果不成立,请写出新的结论,并说明理由.
【解题思路】(1)延长AE,BF交于点F,即可求证△ADE≌△FCE,即可求得CF=AD,AB=BF,即可求得AB=AD+BC;
(2)不成立,新的结论为:AB+BC=AD.延长AE,BF交于点F,可证△ADE≌△FCE和AB=BF,即可解题.
【解答过程】解:(1)延长AE,BF交于点F,
∵AE平分∠BAD,
∴∠BAF=∠DAF,
∵AD∥BC,
∴∠AFB=∠DAF,
∴AB=BF,
在△ADE和△FCE中,
,
∴△ADE≌△FCE(AAS),
∴CF=AD,
∵BF=BC+CF,
∴AB=BC+AD;
(2)不成立,新结论为:AB=AD﹣BC.
延长AE,BF交于点F,
证明:∵AE平分∠BAD,
∴∠BAF=∠DAF,
∵AD∥BC,
∴∠AFB=∠DAF,
∴AB=BF,
在△ADE和△FCE中,
,
∴△ADE≌△FCE(AAS),
∴CF=AD,
∵BF+BC=CF,
∴AB+BC=AD.
28.(2021春 章丘区期末)如图,CD是经过∠BCA顶点C的一条直线,CA=CB,E、F分别是直线CD上两点,且∠BEC=∠CFA=α.
(1)若直线CD经过∠BCA的内部,且E、F在射线CD上.
①如图1,若∠BCA=90°,α=90°,则BE = CF;
②如图2,若0°<∠BCA<180°,请添加一个关于α与∠BCA关系的条件 α+∠BCA=180° ,使①中的结论们然成立,并说明明理由;
(2)如图3,若线CD经过∠BCA的外部,a=∠BCA,请提出关于EF,BE,AF三条线段数量关系的合理猜想,并简述理由.
【解题思路】(1)由∠BCA=90°,∠BEC=∠CFA=α=90°,可得∠CBE=∠ACF,从而可证△BCE≌△CAF,故BE=CF.
(2)若BE=CF,则可使得△BCE≌△CAF.根据题目已知条件添加条件,再使得一对角相等,△BCE≌△CAF便可得证.
(3)题干已知条件可证△BCE≌△CAF,故BE=CF,EC=FA,从而可证明EF=BE+AF.
【解答过程】解:(1)∵∠BEC=∠CFA=α=90°,
∴∠BCE+∠CBE=180°﹣∠BEC=90°.
又∵∠BCA=∠BCE+∠ACF=90°,
∴∠CBE=∠ACF.
在△BCE和△CAF中,
∴△BCE≌△CAF(AAS).
∴BE=CF.
(2)α+∠BCA=180°,理由如下:
∵∠BEC=∠CFA=α,
∴∠BEF=180°﹣∠BEC=180°﹣α.
又∵∠BEF=∠EBC+∠BCE,
∴∠EBC+∠BCE=180°﹣α.
又∵α+∠BCA=180°,
∴∠BCA=180°﹣α.
∴∠BCA=∠BCE+∠ACF=180°﹣α.
∴∠EBC=∠FCA.
在△BCE和△CAF中,
∴△BCE≌△CAF(AAS).
∴BE=CF.
(3)EF=BE+AF,理由如下:
∵∠BCA=α,
∴∠BCE+∠ACF=180°﹣∠BCA=180°﹣α.
又∵∠BEC=α,
∴∠EBC+∠BCE=180°﹣∠BEC=180°﹣α.
∴∠EBC=∠FCA.
在△BEC和△CFA中,
∴△BEC≌△CFA(AAS).
∴BE=CF,EC=FA.
∴EF=EC+CF=FA+BE,即EF=BE+AF.
29.(2020春 南岸区期末)在∠MAN内有一点D,过点D分别作DB⊥AM,DC⊥AN,垂足分别为B,C.且BD=CD,点E,F分别在边AM和AN上.
(1)如图1,若∠BED=∠CFD,请说明DE=DF;
(2)如图2,若∠BDC=120°,∠EDF=60°,猜想EF,BE,CF具有的数量关系,并说明你的结论成立的理由.
【解题思路】(1)根据题目中的条件和∠BED=∠CFD,可以证明△BDE≌△CDF,从而可以得到DE=DF;
(2)作辅助线,过点D作∠CDG=∠BDE,交AN于点G,从而可以得到△BDE≌△CDG,然后即可得到DE=DG,BE=CG,再根据题目中的条件可以得到△EDF≌△GDF,即可得到EF=GF,然后即可得到EF,BE,CF具有的数量关系.
【解答过程】解:(1)∵DB⊥AM,DC⊥AN,
∴∠DBE=∠DCF=90°,
在△BDE和△CDF中,
∵
∴△BDE≌△CDF(AAS).
∴DE=DF;
(2)EF=FC+BE,
理由:过点D作∠CDG=∠BDE,交AN于点G,
在△BDE和△CDG中,
,
∴△BDE≌△CDG(ASA),
∴DE=DG,BE=CG.
∵∠BDC=120°,∠EDF=60°,
∴∠BDE+∠CDF=60°.
∴∠FDG=∠CDG+∠CDF=60°,
∴∠EDF=∠GDF.
在△EDF和△GDF中,
,
∴△EDF≌△GDF(SAS).
∴EF=GF,
∴EF=FC+CG=FC+BE.
30.(2021春 揭东区期末)已知点C为线段AB上一点,分别以AC、BC为边在线段AB同侧作△ACD和△BCE,且CA=CD,CB=CE,∠ACD=∠BCE,直线AE与BD交于点F.
(1)如图1,求证:△ACE≌△DCB.
(2)如图1,若∠ACD=60°,则∠AFB= 120° ;如图2,若∠ACD=90°,则∠AFB= 90° ;
(3)如图3,若∠ACD=β,则∠AFB= 180°﹣β (用含β的式子表示)并说明理由.
【解题思路】(1)求出∠ACE=∠DCB,根据SAS证出两三角形全等即可;
(2)根据全等三角形性质得出∠AEC=∠DBC,∠CDB=∠CAE,求出∠EAB+∠DBA=∠ACD,∠AFB=180°﹣(∠EAB+∠DBC),代入求出即可;
(3)根据全等三角形性质得出∠AEC=∠DBC,∠CDB=∠CAE,求出∠EAB+∠DBA=∠ACD,∠AFB=180°﹣(∠EAB+∠DBC),代入求出即可.
【解答过程】(1)证明:∵∠ACD=∠BCE,
∴∠ACD+∠DCE=∠BCE+∠DCE,
∴∠ACE=∠DCB,
在△ACE和△DCB中
∵,
∴△ACE≌△DCB;
(2)解:∵∠ACD=60°,
∴∠CDB+∠DBC=∠ACD=60°,
∵△ACE≌△DCB,
∴∠AEC=∠DBC,∠CDB=∠CAE,
∴∠CAE+∠DBC=60°,
∴∠AFB=180°﹣60°=120°;
当∠ACD=90°时,
∵∠ACD=90°,
∴∠CDB+∠DBC=∠ACD=90°,
∵△ACE≌△DCB,
∴∠AEC=∠DBC,∠CDB=∠CAE,
∴∠CAE+∠DBC=90°,
∴∠AFB=180°﹣90°=90°;
故答案为:120°,90°;
(3)解:当∠ACD=β时,∠AFB=180°﹣β,理由是:
∵∠ACD=β,
∴∠CDB+∠DBC=∠ACD=β,
∵△ACE≌△DCB,
∴∠AEC=∠DBC,∠CDB=∠CAE,
∴∠CAE+∠DBC=β,
∴∠AFB=180°﹣(∠CAE+∠DBC)=180°﹣β;
故答案为:180°﹣β.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
全等三角形的证明及计算大题专项训练(30道)
1.(2021春 道里区期末)如图,点A,C在EF上,AD∥BC,DE∥BF,AE=CF.
(1)求证:△ADE≌△CBF;
(2)直接写出图中所有相等的线段(AE=CF除外).
2.(2021春 宁德期末)如图,AB,CD交于点O,AC=DB,∠ACD=∠DBA.
(1)说明△AOC≌△DOB的理由;
(2)若∠ACD=94°,∠CAO=28°,求∠OCB的度数.
3.(2021春 沙坪坝区校级期末)如图,在△ABC中,AC=BC,点D在AB边上,点E在BC边上,连接CD,DE.已知∠ACD=∠BDE,CD=DE.
(1)猜想AC与BD的数量关系,并证明你的猜想;
(2)若AD=3,BD=5,求CE的长.
4.(2021春 渝中区校级期末)如图,点E在△ABC的边AC上,且∠ABE=∠C,AF平分∠BAE交BE于F,FD∥BC交AC于点D.
(1)求证:△ABF≌△ADF;
(2)若BE=7,AB=8,AE=5,求△EFD的周长.
5.(2021春 北碚区校级期末)如图,已知D是AC上一点,AB=DA,AB+DC=ED,AE=BC.
(1)求证:△ABC≌△DAE,
(2)若∠BAE=125°,求∠DCB的度数.
6.(2021春 莱芜区期末)如图,已知AD、BC相交于点O,AB=CD,AM⊥BC于点M,DN⊥BC于点N,BN=CM.
(1)求证:△ABM≌△DCN;
(2)试猜想OA与OD的大小关系,并说明理由.
7.(2021春 静安区期末)如图,已知四边形ABCD中,AB∥CD,AD∥BC.E为BD上一点,且BE=AD,∠DEF=∠ADC,EF交BC的延长线于点F.
(1)AD和BC相等吗?为什么?
(2)BF和BD相等吗?为什么?
8.(2021春 沙坪坝区校级月考)如图,△ABC中,CD⊥AB,垂足为D.BE⊥AC,垂足为G,AB=CF,BE=AC.
(1)求证:AE=AF;
(2)求∠EAF的度数.
9.(2021春 铁岭月考)已知:如图,AB=AC,∠1=∠2.
(1)找出图中的所有全等三角形(直接写出);
(2)求证:AD=AE.
10.(2021 南岗区模拟)已知:在△ABC和△DBE中,AB=DB,BC=BE,其中∠ABD=∠CBE.
(1)如图1,求证:AC=DE;
(2)如图2,AB=BC,AC分别交DE,BD于点F,G,BC交DE于点H,在不添加任何辅助线的情况下,请直接写出图2中的四对全等三角形.
11.(2021 三水区一模)如图,AB=AC,直线l过点A,BM⊥直线l,CN⊥直线l,垂足分别为M、N,且BM=AN.
(1)求证△AMB≌△CNA;
(2)求证∠BAC=90°.
12.(2021 广州模拟)如图,在△ABC中,∠ACB=90°,AC=BC,点E是∠ACB内部一点,连接CE,作AD⊥CE,BE⊥CE,垂足分别为点D,E.
(1)求证:△BCE≌△CAD;
(2)若BE=5,DE=7,则△ACD的周长是 .
13.(2020春 越秀区校级期中)已知:△ABN和△ACM的位置如图所示,∠1=∠2,AB=AC,AM=AN.
求证:(1)∠BAN=∠CAM;
(2)∠ODA=∠OEA.
14.(2020 江北区模拟)如图,在△ABC中,AD是BC边上的中线,E是AB边上一点,过点C作CF∥AB,交ED的延长线于点F.
(1)求证:△BDE≌△CDF;
(2)当AD⊥BC,AE=2,CF=1时,求AC的长.
15.(2020秋 萧山区月考)如图,已知在△ABC中,BD⊥AC于D,CE⊥AB于E,F是BD上一点,BF=AC,G是CE延长线上一点,CG=AB,连接AG,AF.
(1)试说明∠ABD=∠ACE;
(2)探求线段AF,AG有什么关系?并请说明理由.
16.(2021 张家界模拟)如图,四边形ABCD中,AB=BC=2CD,AB∥CD,∠C=90°,E是BC的中点,AE与BD相交于点F,连接DE
(1)求证:△ABE≌△BCD;
(2)判断线段AE与BD的数量关系及位置关系,并说明理由;
(3)若CD=1,试求△AED的面积.
17.(2020秋 台江区校级期中)如图,A,B,C三点共线,D,C,E三点共线,∠A=∠DBC,EF⊥AC于点F,AE=BD.
(1)求证:C是DE的中点;
(2)求证:AB=2CF.
18.(2021春 铁岭月考)如图,△AOC和△BOD中,OA=OC,OB=OD,∠AOC=∠BOD=α(0<α<90°),AD与BC交于点P.
(1)求证:△AOD≌△COB;
(2)求∠APC(用含α的式子表示);
(3)过点O分别作OM⊥AD,ON⊥BC,垂足分别为点M、N,请直接写出OM和ON的数量关系.
19.(2020秋 花都区月考)如图所示,BD、CE是△ABC的高,点P在BD的延长线上,CA=BP,点Q在CE上,QC=AB.
(1)探究PA与AQ之间的关系;
(2)若把(1)中的△ABC改为钝角三角形,AC>AB,∠A是钝角,其他条件不变,上述结论是否成立?画出图形并证明你的结论.
20.(2020春 萍乡期末)在△ABC中,AB=AC,D是直线BC上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE,设∠BAC=∠1,∠DCE=∠2.
(1)如图①,当点D在线段BC上移动时,试说明:∠1+∠2=180°;
(2)如图②,当点D在线段BC的延长线上移动时,请猜测∠1与∠2有怎样的数量关系?并说明理由.
21.(2020春 揭阳期末)已知△ABC,点D、F分别为线段AC、AB上两点,连接BD、CF交于点E.
(1)若BD⊥AC,CF⊥AB,如图1所示,试说明∠BAC+∠BEC=180°;
(2)若BD平分∠ABC,CF平分∠ACB,如图2所示,试说明此时∠BAC与∠BEC的数量关系;
(3)在(2)的条件下,若∠BAC=60°,试说明:EF=ED.
22.(2020秋 淇滨区校级期中)(1)如图1所示,△ACB和△ECD都是等腰三角形,A、C、D三点在同一直线上,连接BD、AE,并延长AE交BD于点F,试判断AE与BD的数量关系及位置关系,并证明你的结论.
(2)若△ECD绕顶点C顺时针转任意角度后得到图2,图1中的结论是否仍然成立?请说明理由.
23.(2020秋 蒙阴县期中)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.
(1)当直线MN绕着点C旋转到如图1所示的位置时,
求证:①△ADC≌△CEB;
②DE=AD+BE;
(2)当直线MN绕着点C旋转到如图2所示的位置时,
①找出图中一对全等三角形;
②DE、AD、BE之间有怎样的数量关系,并加以证明.
24.(2020秋 环翠区期末)(1)如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,若∠EAF∠BAD,可求得EF、BE、FD之间的数量关系为 .(只思考解题思路,完成填空即可,不必书写证明过程)
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,若∠EAF∠BAD,判断EF、BE、FD之间的数量关系还成立吗,若成立,请完成证明,若不成立,请说明理由.【可借鉴第(1)问的解题经验】
25.(2021春 和平区期末)如图,在△ABC中,AC=BC,点D在边AB上,AB=4BD,连接CD,点E,F在线段CD上,连接BF,AE,∠BFC=∠AEC=180°﹣∠ACB.
(1)①∠FBC与∠ECA相等吗?说明你的理由;
②△FBC与△ECA全等吗?说明你的理由;
(2)若AE=11,EF=8,则请直接写出BF的长为 ;
(3)若△ACE与△BDF的面积之和为12,则△ABC的面积为 .
26.(2020 岱岳区一模)已知∠ABC=90°,点D是直线AB边上的点,AD=BC.
(1)如图1,点D在线段AB上,过点A作AF⊥AB,且AF=BD,连接DC、DF、CF,试判断△CDF的形状并说明理由;
(2)如图2,点D在线段AB的延长线上,点F在点A的左侧,其他条件不变,以上结论是否仍然成立?请说明理由.
27.如图(1),线段AD∥BC,连接AB、CD,取CD中点E,连接AE,AE平分∠BAD.
(1)线段AB与AD、BC之间存在怎样的等量关系?请说明理由.
(2)如果点C在AB的左侧,其他条件不变,如图(2)所示,那么(1)中的结论还成立吗?如果成立,请说明理由;如果不成立,请写出新的结论,并说明理由.
28.(2021春 章丘区期末)如图,CD是经过∠BCA顶点C的一条直线,CA=CB,E、F分别是直线CD上两点,且∠BEC=∠CFA=α.
(1)若直线CD经过∠BCA的内部,且E、F在射线CD上.
①如图1,若∠BCA=90°,α=90°,则BE CF;
②如图2,若0°<∠BCA<180°,请添加一个关于α与∠BCA关系的条件 ,使①中的结论们然成立,并说明明理由;
(2)如图3,若线CD经过∠BCA的外部,a=∠BCA,请提出关于EF,BE,AF三条线段数量关系的合理猜想,并简述理由.
29.(2020春 南岸区期末)在∠MAN内有一点D,过点D分别作DB⊥AM,DC⊥AN,垂足分别为B,C.且BD=CD,点E,F分别在边AM和AN上.
(1)如图1,若∠BED=∠CFD,请说明DE=DF;
(2)如图2,若∠BDC=120°,∠EDF=60°,猜想EF,BE,CF具有的数量关系,并说明你的结论成立的理由.
30.(2021春 揭东区期末)已知点C为线段AB上一点,分别以AC、BC为边在线段AB同侧作△ACD和△BCE,且CA=CD,CB=CE,∠ACD=∠BCE,直线AE与BD交于点F.
(1)如图1,求证:△ACE≌△DCB.
(2)如图1,若∠ACD=60°,则∠AFB= ;如图2,若∠ACD=90°,则∠AFB= ;
(3)如图3,若∠ACD=β,则∠AFB= (用含β的式子表示)并说明理由.
全等三角形的证明及计算大题专项训练(30道)
1.(2021春 道里区期末)如图,点A,C在EF上,AD∥BC,DE∥BF,AE=CF.
(1)求证:△ADE≌△CBF;
(2)直接写出图中所有相等的线段(AE=CF除外).
【解题思路】(1)利用ASA证明△ADE≌△CBF即可;
(2)根据△ADE≌△CBF即可得图中所有相等的线段.
【解答过程】(1)证明:∵AD∥BC
∴∠DAC=∠BCA,
又∵∠DAC+∠EAD=180°,∠BCA+∠FCB=180°,
∴∠EAD=∠FCB,
∵DE∥BF,
∴∠E=∠F,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(ASA),
(2)∵△ADE≌△CBF,
∴ED=FB,DA=BC,EC=FA.
∵AD∥BC,
∴∠DAC=∠BCA,
在△ADC和△CBA中,
,
∴△ADC≌△CBA(SAS),
∴AB=CD;
∴图中所有相等的线段有:ED=FB,DA=BC,AB=CD,EC=FA.
2.(2021春 宁德期末)如图,AB,CD交于点O,AC=DB,∠ACD=∠DBA.
(1)说明△AOC≌△DOB的理由;
(2)若∠ACD=94°,∠CAO=28°,求∠OCB的度数.
【解题思路】(1)直接利用AAS即可证明△AOC≌△DOB;
(2)利用三角形外角的性质得到∠COB,再根据△AOC≌△DOB得到OC=OB,即可求得∠OCB.
【解答过程】解:(1)在△AOC和△DOB中,
,
∴△AOC≌△DOB(AAS);
(2)∵∠ACD=94°,∠CAO=28°,
∴∠COB=∠ACD+∠CAO=122°,
∵△AOC≌△DOB,
∴OC=OB,
∴∠OCB=(180°﹣122°)÷2=29°.
3.(2021春 沙坪坝区校级期末)如图,在△ABC中,AC=BC,点D在AB边上,点E在BC边上,连接CD,DE.已知∠ACD=∠BDE,CD=DE.
(1)猜想AC与BD的数量关系,并证明你的猜想;
(2)若AD=3,BD=5,求CE的长.
【解题思路】(1)利用AAS证明△ADC≌△BED,即可得结论;
(2)结合△ADC≌△BED,可得AC=BD=5,BE=AD=3,进而可得CE的长.
【解答过程】解:(1)AC=BD,理由如下:
∵AC=BC,
∴∠A=∠B,
在△ADC和△BED中,
,
∴△ADC≌△BED(AAS),
∴AC=BD;
(2)由(1)知:△ADC≌△BED,
∴AC=BD=5,BE=AD=3,
∴BC=AC=5,
∴CE=BC﹣BE=2.
4.(2021春 渝中区校级期末)如图,点E在△ABC的边AC上,且∠ABE=∠C,AF平分∠BAE交BE于F,FD∥BC交AC于点D.
(1)求证:△ABF≌△ADF;
(2)若BE=7,AB=8,AE=5,求△EFD的周长.
【解题思路】(1)根据平行线的性质得到∠ADF=∠C,等量代换得到∠ABF=∠ADF,由角平分线的定义得到∠BAF=∠CAF,根据全等三角形的判定定理即可得到结论;
(2)根据全等三角形的性质得到AD=AB=8,BF=DF,由线段的和差得到DE=AD=AE=8﹣5=3,根据三角形的周长公式即可得到结论.
【解答过程】解:(1)∵FD∥BC,
∴∠ADF=∠C,
∵∠ABF=∠C,
∴∠ABF=∠ADF,
∵AF平分∠BAE,
∴∠BAF=∠CAF,
在△ABF和△ADF中,
,
∴△ABF≌△ADF(AAS);
(2)∵△ABF≌△ADF,
∴AD=AB=8,BF=DF,
∵AE=5,
∴DE=AD﹣AE=8﹣5=3,
∴△EFD的周长=EF+DF+DE=EF+BF+DE=BE+DE=7+3=10.
5.(2021春 北碚区校级期末)如图,已知D是AC上一点,AB=DA,AB+DC=ED,AE=BC.
(1)求证:△ABC≌△DAE,
(2)若∠BAE=125°,求∠DCB的度数.
【解题思路】(1)根据SSS证明三角形全等即可.
(2)利用全等三角形的性质以及三角形内角和定理求解即可.
【解答过程】(1)证明:∵DE=AB+DC,AB=AD,
∴DE=AD+DC=AC,
在△ABC和△DAE中,
,
∴△ABC≌△DAE(SSS).
(2)解:∵△ABC≌△DAE,
∴∠EAD=∠B,
∴∠B+∠BAC=∠EAD+∠BAC=∠EAB=125°,
∴∠DCB=180°﹣(∠B+∠BAC)=180°﹣125°=55°.
6.(2021春 莱芜区期末)如图,已知AD、BC相交于点O,AB=CD,AM⊥BC于点M,DN⊥BC于点N,BN=CM.
(1)求证:△ABM≌△DCN;
(2)试猜想OA与OD的大小关系,并说明理由.
【解题思路】(1)根据HL可证明:△ABM≌△DCN;
(2)根据AAS证明△AMO≌△DNO可得结论.
【解答过程】(1)证明:∵BN=CM,
∴BN+MN=MN+CM,
即CN=BM,
∵AM⊥BC于点M,DN⊥BC于点N,
∴∠AMB=∠DNC=90°,
在Rt△ABM和Rt△DCN中,
,
∴Rt△ABM≌Rt△DCN(HL);
(2)解:OA=OD,理由如下:
∵Rt△ABM≌Rt△DCN,
∴AM=DN,
在△AMO和△DNO中,
,
∴△AMO≌△DNO(AAS),
∴OA=OD.
7.(2021春 静安区期末)如图,已知四边形ABCD中,AB∥CD,AD∥BC.E为BD上一点,且BE=AD,∠DEF=∠ADC,EF交BC的延长线于点F.
(1)AD和BC相等吗?为什么?
(2)BF和BD相等吗?为什么?
【解题思路】(1)根据平行线的性质和全等三角形的判定和性质得出△ABD与△CDB全等,进而利用全等三角形的性质解答即可;
(2)根据平行线的性质和全等三角形的判定和性质得出△EFB与△CDB全等,进而解答即可.
【解答过程】解:(1)AD=CB,理由如下:
∵AD∥BC,
∴∠ABD=∠CDB,
同理可得,∠ADB=∠CBD,
在△ABD与△CDB中,
,
∴△ABD≌△CDB(ASA),
∴AD=CB;
(2)BF=BD,理由如下:
∵AD=CB,BE=AD,
∴BC=BE,
∵∠DEF=∠ADC,
∴∠DEF﹣∠DBF=∠ADC﹣∠ADB,
即∠EFB=∠CDB,
在△EFB与△CDB中,
,
∴△EFB≌△CDB(ASA),
∴FB=DB.
8.(2021春 沙坪坝区校级月考)如图,△ABC中,CD⊥AB,垂足为D.BE⊥AC,垂足为G,AB=CF,BE=AC.
(1)求证:AE=AF;
(2)求∠EAF的度数.
【解题思路】(1)利用SAS证明△AEB≌△FAC可证明结论;
(2)由全等三角形的性质可得∠E=∠CAF,由余角的定义可求得∠EAF的度数.
【解答过程】(1)证明:∵CD⊥AB,BE⊥AC,
∴∠CAD+∠ACD=∠CAD+∠EBA=90°,
∴∠ACD=∠EBA,
在△AEB和△FAC中,
,
∴△AEB≌△FAC(SAS),
∴AE=FA;
(2)解:∵△AEB≌△FAC,
∴∠E=∠CAF,
∵∠E+∠EAG=90°,
∴∠CAF+∠EAG=90°,
即∠EAF=90°.
9.(2021春 铁岭月考)已知:如图,AB=AC,∠1=∠2.
(1)找出图中的所有全等三角形(直接写出);
(2)求证:AD=AE.
【解题思路】(1)直接根据全等三角形的判定可得答案;
(2)先根据SAS证得△ABF≌△ACF,再根据ASA证得△BDF≌△CEF,然后根据全等三角形的性质可得结论.
【解答过程】解:(1)△ABF≌△ACF,△BDF≌△CEF,△ADF≌△AEF,△ADC≌△AEB;
(2)证明:在△ABF和△ACF中,
,
∴△ABF≌△ACF(SAS),
∴∠B=∠C,BF=CF.
在△BDF和△CEF中,
,
∴△BDF≌△CEF(ASA),
∴BD=CE,
∴AB﹣BD=AC﹣CE,
∴AD=AE.
10.(2021 南岗区模拟)已知:在△ABC和△DBE中,AB=DB,BC=BE,其中∠ABD=∠CBE.
(1)如图1,求证:AC=DE;
(2)如图2,AB=BC,AC分别交DE,BD于点F,G,BC交DE于点H,在不添加任何辅助线的情况下,请直接写出图2中的四对全等三角形.
【解题思路】(1)根据SAS证明△ABC与△DBE全等,利用全等三角形的性质解答即可.
(2)根据全等三角形的判定解答即可.
【解答过程】证明:(1)∵∠ABD=∠CBE,
∴∠ABD+∠DBC=∠CBE+∠DBC,
即∠ABC=∠DBE,
在△ABC与△DBE中,
,
∴△ABC≌△DBE(SAS),
∴AC=DE;
(2)由(1)得△ABC≌△DBE,
∴∠A=∠D,∠C=∠E,AB=DB,BC=BE,
∴AB=BE,
∵AB=BC,
∴∠A=∠C,
∴∠A=∠E,
在△ABG与△EBH中,
,
∴△ABG≌△EBH(ASA),
∴BG=BH,
在△DBH与△CBG中,
,
∴△DBH≌△CBG(SAS),
∴∠D=∠C,
∵DB=CB,BG=BH,
∴DG=CH,
在△DFG与△CFH中,
,
∴△DFG≌△CFH(AAS).
11.(2021 三水区一模)如图,AB=AC,直线l过点A,BM⊥直线l,CN⊥直线l,垂足分别为M、N,且BM=AN.
(1)求证△AMB≌△CNA;
(2)求证∠BAC=90°.
【解题思路】(1)由HL证明△AMB≌△CNA即可;
(2)先由全等三角形的性质得∠BAM=∠ACN,再由∠CAN+∠ACN=90°,得∠CAN+∠BAM=90°,即可得出结论.
【解答过程】证明:(1)∵BM⊥直线l,CN⊥直线l,
∴∠AMB=∠CNA=90°,
在Rt△AMB和Rt△CNA中,
,
∴Rt△AMB≌Rt△CNA(HL);
(2)由(1)得:Rt△AMB≌Rt△CNA,
∴∠BAM=∠ACN,
∵∠CAN+∠ACN=90°,
∴∠CAN+∠BAM=90°,
∴∠BAC=180°﹣90°=90°.
12.(2021 广州模拟)如图,在△ABC中,∠ACB=90°,AC=BC,点E是∠ACB内部一点,连接CE,作AD⊥CE,BE⊥CE,垂足分别为点D,E.
(1)求证:△BCE≌△CAD;
(2)若BE=5,DE=7,则△ACD的周长是 30 .
【解题思路】(1)根据条件可以得出∠E=∠ADC=90°,进而得出△CEB≌△ADC;
(2)利用(1)中结论,根据全等三角形的性质即可解决问题;
【解答过程】(1)证明:∵BE⊥CE,AD⊥CE,
∴∠E=∠ADC=90°,
∴∠EBC+∠BCE=90°.
∵∠BCE+∠ACD=90°,
∴∠EBC=∠DCA.
在△BCE和△CAD中,
,
∴△BCE≌△CAD(AAS);
(2)解:∵:△BCE≌△CAD,BE=5,DE=7,
∴BE=DC=5,CE=AD=CD+DE=5+7=12.
∴由勾股定理得:AC=13,
∴△ACD的周长为:5+12+13=30,
故答案为:30.
13.(2020春 越秀区校级期中)已知:△ABN和△ACM的位置如图所示,∠1=∠2,AB=AC,AM=AN.
求证:(1)∠BAN=∠CAM;
(2)∠ODA=∠OEA.
【解题思路】(1)由∠1=∠2,则∠1+∠MAN=∠2+∠MAN,即∠BAN=∠CAM;
(2)先证△ACM≌△ABN(SAS),得∠M=∠N,再证△ADN≌△AEM(ASA),即可得出结论.
【解答过程】证明:(1)∵∠1=∠2,
∴∠1+∠MAN=∠2+∠MAN,
即∠BAN=∠CAM;
(2)在△ACM和△ABN中,
,
∴△ACM≌△ABN(SAS),
∴∠M=∠N,
在△ADN和△AEM中,
,
∴△ADN≌△AEM(ASA),
∴∠NDA=∠MEA,
即∠ODA=∠OEA.
14.(2020 江北区模拟)如图,在△ABC中,AD是BC边上的中线,E是AB边上一点,过点C作CF∥AB,交ED的延长线于点F.
(1)求证:△BDE≌△CDF;
(2)当AD⊥BC,AE=2,CF=1时,求AC的长.
【解题思路】(1)根据平行线的性质得到∠B=∠FCD,∠BED=∠F,由AD是BC边上的中线,得到BD=CD,于是得到结论;
(2)根据全等三角形的性质得到BE=CF=1,求得AB=AE+BE=3,于是得到结论.
【解答过程】证明:∵CF∥AB,
∴∠B=∠FCD,∠BED=∠F,
∵AD是BC边上的中线,
∴BD=CD,在△BDE和△CDF中,
,
∴△BDE≌△CDF(AAS);
(2)∵△BDE≌△CDF,
∴BE=CF=1,
∴AB=AE+BE=2+1=3,
∵AD⊥BC,BD=CD,
∴AC=AB=3.
15.(2020秋 萧山区月考)如图,已知在△ABC中,BD⊥AC于D,CE⊥AB于E,F是BD上一点,BF=AC,G是CE延长线上一点,CG=AB,连接AG,AF.
(1)试说明∠ABD=∠ACE;
(2)探求线段AF,AG有什么关系?并请说明理由.
【解题思路】(1)根据的等角的余角相等,即可证明∠ACG=∠ABF;
(2)根据SAS推出△ABF≌△GCA即可解决问题;
【解答过程】(1)证明:∵BD、CE是△ABC的高,
∴∠ADB=∠AEC=90°,
∴∠ABF+∠BAD=90°,∠GCA+∠BAD=90°,
∴∠ABF=∠GCA,
(2)结论:AF=AG,AF⊥AG.理由如下:
在△ABF和△GCA中,
,
∴△ABF≌△GCA(SAS),
∴AF=AG,∠GAC=∠AFB,
∵∠AFB=∠ADB+∠FAD,∠GAC=∠GAF+∠FAD,
∴∠GAF=∠ADF,
∵∠ADF=90°,
∴∠GAF=90°,
∴AG⊥AF,AG=AF.
16.(2021 张家界模拟)如图,四边形ABCD中,AB=BC=2CD,AB∥CD,∠C=90°,E是BC的中点,AE与BD相交于点F,连接DE
(1)求证:△ABE≌△BCD;
(2)判断线段AE与BD的数量关系及位置关系,并说明理由;
(3)若CD=1,试求△AED的面积.
【解题思路】(1)由平行线的性质得出∠ABE+∠C=180°,得出∠ABE=90°=∠C,再证出BE=CD,由SAS证明△ABE≌△BCD即可;
(2)由全等三角形的性质得出AE=BD,证出∠ABF+∠BAE=90°,得出∠AFB=90°,即可得出结论;
(3)由全等三角形的性质得出BE=CD=1,求出CE=BC﹣BE=1,得出CE=CD,△AED的面积=梯形ABCD的面积﹣△ABE的面积﹣△CDE的面积,即可得出答案.
【解答过程】(1)证明:∵AB∥CD,
∴∠ABE+∠C=180°,
∵∠C=90°,
∴∠ABE=90°=∠C,
∵E是BC的中点,
∴BC=2BE,
∵BC=2CD,
∴BE=CD,
在△ABE和△BCD中,,
∴△ABE≌△BCD(SAS);
(2)解:AE=BD,AE⊥BD,理由如下:
由(1)得:△ABE≌△BCD,
∴AE=BD,
∵∠BAE=∠CBD,∠ABF+∠CBD=90°,
∴∠ABF+∠BAE=90°,
∴∠AFB=90°,
∴AE⊥BD;
(3)解:∵△ABE≌△BCD,
∴BE=CD=1,
∵AB=BC=2CD=2,
∴CE=BC﹣BE=1,
∴CE=CD,
∴△AED的面积=梯形ABCD的面积﹣△ABE的面积﹣△CDE的面积(1+2)×22×11×1.
17.(2020秋 台江区校级期中)如图,A,B,C三点共线,D,C,E三点共线,∠A=∠DBC,EF⊥AC于点F,AE=BD.
(1)求证:C是DE的中点;
(2)求证:AB=2CF.
【解题思路】(1)过D作DH⊥AC的延长线与H,根据全等三角形的判定证得△AEF≌△BDH,得到EF=DH,再证得△EFC≌△DHC得到CE=CD,即可证得即可证得结论;
(2)由(1)得,△AEF≌△BDH,△EFC≌△DHC,根据全等三角形的性质得到AF=BH,CF=CH,再根据线段的和差即可证得结论.
【解答过程】证明:(1)过D作DH⊥AC的延长线与H,
∴∠EFC=∠DHC=90°,
在△AEF和△BDH中,
,
∴△AEF≌△BDH(AAS),
∴EF=DH,
在△EFC和△DHC中,
,
∴△EFC≌△DHC(AAS),
∴CE=CD,
∴C是DE的中点;
(2)由(1)得,△AEF≌△BDH,△EFC≌△DHC,
∴AF=BH,CF=CH,
∴AB+BF=BF+FH,FH=2FC,
∴AB=FH,
∴AB=2CF.
18.(2021春 铁岭月考)如图,△AOC和△BOD中,OA=OC,OB=OD,∠AOC=∠BOD=α(0<α<90°),AD与BC交于点P.
(1)求证:△AOD≌△COB;
(2)求∠APC(用含α的式子表示);
(3)过点O分别作OM⊥AD,ON⊥BC,垂足分别为点M、N,请直接写出OM和ON的数量关系.
【解题思路】(1)由∠AOC=∠BOD,可得∠AOD=∠COB,然后根据SAS可得结论;
(2)根据全等三角形的性质得∠OAD=∠OCB,再根据三角形外角性质可得答案;
(3)根据全等三角形的性质得∠MAO=∠NCO,由垂直定义得∠AMO=∠CNO,再根据全等三角形的判定与性质可得结论.
【解答过程】解:(1)∵∠AOC=∠BOD,
∴∠AOC+∠COD=∠BOD+∠COD,
∴∠AOD=∠COB,
在△AOD和△COB中,
,
∴△AOD≌△COB(SAS);
(2)由(1)可知△AOD≌△COB,
∴∠OAD=∠OCB,
令AD与OC交于点E,
则∠AEC=∠OAD+∠AOC=∠OCB+∠APC,
∴∠AOC=∠APC,
∵∠AOC=α,
∴∠APC=α;
(3)∵△AOD≌△COB,
∴∠PAP=∠BCO,即∠MAO=∠NCO,
∵OM⊥AD,ON⊥BC,
∴∠AMO=∠CNO=90°,
在△AOM和△CON中,
,
∴△AOM≌△CON(AAS),
∴OM=ON.
19.(2020秋 花都区月考)如图所示,BD、CE是△ABC的高,点P在BD的延长线上,CA=BP,点Q在CE上,QC=AB.
(1)探究PA与AQ之间的关系;
(2)若把(1)中的△ABC改为钝角三角形,AC>AB,∠A是钝角,其他条件不变,上述结论是否成立?画出图形并证明你的结论.
【解题思路】(1)由条件可得出∠1=∠2,可证得△APB≌△QAC,可得结论;
(2)根据题意画出图形,结合(1)可证得△APB≌△QAC,可得结论.
【解答过程】(1)结论:AP=AQ,AP⊥AQ
证明:∵BD、CE是△ABC的高,
∴BD⊥AC,CE⊥AB,
∴∠1+∠CAB=90°,∠2+∠CAB=90°,
∴∠1=∠2,
在△QAC和△APB中,
,
∴△QAC≌△APB(SAS),
∴AQ=AP,∠QAC=∠P,
而∠DAP+∠P=90°,
∴∠DAP+∠QAC=90°,
即∠QAP=90°,
∴AQ⊥AP;
即AP=AQ,AP⊥AQ;
(2)上述结论成立,理由如下:
如图所示:
∵BD、CE是△ABC的高,
∴BD⊥AC,CE⊥AB,
∴∠1+∠CAE=90°,∠2+∠DAB=90°,
∵∠CAE=∠DAB,
∴∠1=∠2,
在△QAC和△APB中,
,
∴△QAC≌△APB(SAS),
∴AQ=AP,∠QAC=∠P,
∵∠PDA=90°,
∴∠P+∠PAD=90°,
∴∠QAC+∠PAD=90°,
∴∠QAP=90°,
∴AQ⊥AP,
即AP=AQ,AP⊥AQ.
20.(2020春 萍乡期末)在△ABC中,AB=AC,D是直线BC上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE,设∠BAC=∠1,∠DCE=∠2.
(1)如图①,当点D在线段BC上移动时,试说明:∠1+∠2=180°;
(2)如图②,当点D在线段BC的延长线上移动时,请猜测∠1与∠2有怎样的数量关系?并说明理由.
【解题思路】(1)由“SAS”可证△BAD≌△CAE,可得∠ACE=∠ABD,由三角形的内角和定理可得结论;
(2)由“SAS”可证△BAD≌△CAE,可得∠ACE=∠ABD,由三角形的内角和定理和平角的定义可得结论.
【解答过程】证明:(1)∵∠DAE=∠BAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△BAD≌△CAE(SAS),
∴∠ACE=∠ABD,
∵∠BAC+∠ABD+∠ACB=180°,
∴∠BAC+∠ACB+∠ACE=∠BAC+∠BCE=180°,
∴∠1+∠2=180°;
(2)∠1=∠2,
理由如下:∵∠DAE=∠BAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△BAD≌△CAE(SAS),
∴∠ACE=∠ABD,
∵∠BAC+∠ABD+∠ACB=180°,∠ACE+∠ACB+∠DCE=180°,
∴∠1=∠2.
21.(2020春 揭阳期末)已知△ABC,点D、F分别为线段AC、AB上两点,连接BD、CF交于点E.
(1)若BD⊥AC,CF⊥AB,如图1所示,试说明∠BAC+∠BEC=180°;
(2)若BD平分∠ABC,CF平分∠ACB,如图2所示,试说明此时∠BAC与∠BEC的数量关系;
(3)在(2)的条件下,若∠BAC=60°,试说明:EF=ED.
【解题思路】(1)根据余角的性质得到∠DEC=∠BAC,由于∠DEC+∠BEC=180°,即可得到结论;
(2)根据角平分线的性质得到∠EBCABC,∠ECBACB,于是得到结论;
(3)作∠BEC的平分线EM交BC于M,由∠BAC=60°,得到∠BEC=90°BAC=120°,求得∠FEB=∠DEC=60°,根据角平分线的性质得到∠BEM=60°,推出△FBE≌△EBM,根据全等三角形的性质得到EF=EM,同理DE=EM,即可得到结论.
【解答过程】解:(1)∵BD⊥AC,CF⊥AB,
∴∠DCE+∠DEC=∠DCE+∠FAC=90°,
∴∠DEC=∠BAC,∠DEC+∠BEC=180°,
∴∠BAC+∠BEC=180°;
(2)∵BD平分∠ABC,CF平分∠ACB,
∴∠EBCABC,∠ECBACB,∠BEC=180°﹣(∠EBC+∠ECB)=180°(∠ABC+∠ACB)=180°(180°﹣∠BAC)=90°∠BAC;
(3)作∠BEC的平分线EM交BC于M,
∵∠BAC=60°,
∴∠BEC=90°BAC=120°,
∴∠FEB=∠DEC=60°,
∵EM平分∠BEC,
∴∠BEM=60°,
在△FBE与△EBM中,
,
∴△FBE≌△EBM(ASA),
∴EF=EM,同理DE=EM,
∴EF=DE.
22.(2020秋 淇滨区校级期中)(1)如图1所示,△ACB和△ECD都是等腰三角形,A、C、D三点在同一直线上,连接BD、AE,并延长AE交BD于点F,试判断AE与BD的数量关系及位置关系,并证明你的结论.
(2)若△ECD绕顶点C顺时针转任意角度后得到图2,图1中的结论是否仍然成立?请说明理由.
【解题思路】(1)根据SAS推出△ACE≌△BCD,根据全等三角形的性质得出∠CAE=∠DBC,根据∠ACB=90°求出∠CAE+∠AEC=90°,求出∠DBC+∠BEF=90°,根据三角形内角和定理求出∠BFE=90°即可;
(2)根据SAS推出△ACE≌△BCD,根据全等三角形的性质得出∠CAE=∠DBC,根据∠ACB=90°求出∠CAE+∠AOC=90°,求出∠DBC+∠BOE=90°,根据三角形内角和定理求出∠BFO=90°即可.
【解答过程】(1)AE⊥BD.
证明:在△ACE和△BCD中
∴△ACE≌△BCD(SAS),
∴∠CAE=∠DBC,
∵∠ACB=90°,
∴∠CAE+∠AEC=90°,
∵∠CAE=∠DBC,∠AEC=∠BEF,
∴∠DBC+∠BEF=90°,
∴∠BFE=180°﹣90°=90°,
∴AE⊥BD;
(2)解:结论还成立,
理由是:∵∠ACB=∠ECD,
∴∠ACB+∠BCE=∠ECD+∠BCE,
即∠ACE=∠BCD,
在△ACE和△BCD中
∴△ACE≌△BCD(SAS),
∴∠CAE=∠DBC,
∵∠ACB=90°,
∴∠CAE+∠AOC=90°,
∵∠CAE=∠DBC,∠AOC=∠BOE,
∴∠DBC+∠BOE=90°,
∴∠BFO=180°﹣90°=90°,
∴AE⊥BD.
23.(2020秋 蒙阴县期中)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.
(1)当直线MN绕着点C旋转到如图1所示的位置时,
求证:①△ADC≌△CEB;
②DE=AD+BE;
(2)当直线MN绕着点C旋转到如图2所示的位置时,
①找出图中一对全等三角形;
②DE、AD、BE之间有怎样的数量关系,并加以证明.
【解题思路】(1)根据余角和补角的性质易证得∠DAC=∠ECB,已知∠ADC=∠CEB=90°,AC=CB,根据全等三角形的判定AAS即可证明△ADC≌△CEB,根据各边的相等关系即可得DE=AD+BE.
(2)同理可证得△ADC≌△CEB,再根据各边的相等关系可得DE=AD﹣BE.
【解答过程】(1)证明:∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90°,
∴∠DAC+∠ACD=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=180°﹣90°=90°,
∴∠DAC=∠ECB;
在△ADC和△CEB中,∠ADC=∠CEB,∠DAC=∠ECB,AC=CB,
∴△ADC≌△CEB(AAS)①,(7分)
∴DC=EB,AD=CE,
∴DE=AD+BE.(9分)
(2)解:同理可得△ADC≌△CEB①;(11分)
∴AD=CE,CD=BE,
∴DE=AD﹣BE②.(14分)
24.(2018秋 环翠区期末)(1)如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,若∠EAF∠BAD,可求得EF、BE、FD之间的数量关系为 BE+DF=EF .(只思考解题思路,完成填空即可,不必书写证明过程)
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,若∠EAF∠BAD,判断EF、BE、FD之间的数量关系还成立吗,若成立,请完成证明,若不成立,请说明理由.【可借鉴第(1)问的解题经验】
【解题思路】(1)线段EF、BE、FD之间的数量关系是BE+DF=EF.如图1中,延长CB至M,使BM=DF,连接AM,利用全等三角形的性质解决问题即可.
(2)结论:EF+DF=BE.如图2中,在BE上截取BM=DF,连接AM,证明△ABM≌△ADF(SAS),推出AM=AF,∠BAM=∠DAF,再证明△AEM≌△AEF(SAS),可得结论.
【解答过程】解:(1)线段EF、BE、FD之间的数量关系是BE+DF=EF.
如图1,延长CB至M,使BM=DF,连接AM,
∵∠ABC+∠D=180°,∠ABC+∠1=180°,
∴∠1=∠D,
在△ABM和△ADF中,
,
∴△ABM≌△ADF(SAS),
∴AM=AF,∠3=∠2,
∵∠EAF∠BAD,
∴∠4+∠4=∠EAF,
∴∠GAM=∠3+∠4=∠2+∠4=∠EAF,
在△MAE和△FAE中,
,
∴△MAE≌△FAE(SAS),
∴EF=EM,
∵EM=BM+BE=BE+DF,
∴EF=BE+FD;
故答案为:BE+DF=EF.
(2)结论:EF+DF=BE.
理由:在BE上截取BM=DF,连接AM,
∵∠B+∠ADC=180°,∠ADC+∠ADE=180°,
∴∠B=∠ADF,
在△ABM与△ADF中,
,
∴△ABM≌△ADF(SAS),
∴AM=AF,∠BAM=∠DAF,
∵,
∴∠EAF=∠EAM,
在△AEM与△AEF中,
,
∴△AEM≌△AEF(SAS),
∴EM=EF,
即BE﹣BM=EF,
即BE﹣DF=EF,
∴EF+DF=BE.
25.(2021春 和平区期末)如图,在△ABC中,AC=BC,点D在边AB上,AB=4BD,连接CD,点E,F在线段CD上,连接BF,AE,∠BFC=∠AEC=180°﹣∠ACB.
(1)①∠FBC与∠ECA相等吗?说明你的理由;
②△FBC与△ECA全等吗?说明你的理由;
(2)若AE=11,EF=8,则请直接写出BF的长为 3 ;
(3)若△ACE与△BDF的面积之和为12,则△ABC的面积为 48 .
【解题思路】(1)①连接BC,由已知及∠AEC=180°﹣∠AED,可得到∠ACB=∠AED.再证明∠CAE=∠BCF,由三角形内角和定理可得∠FBC=∠ECA;②利用“ASA”证明△FBC≌△ECA;
(2)由(1)中全等三角形的结论及已知可得到BF的长;
(3)由(1)中结论可得S△FBC=S△ECA,所以S△ECA+S△BDF=12=S△FBC+S△BDF=S△DBC,根据AB=4BD,可得到S△DBCS△ABC=12,从而可得△ABC的面积.
【解答过程】解:(1)①∠FBC=∠ECA,理由如下:
连接BC,如右图.
∵∠BFC=∠AEC=180°﹣∠ACB,且∠AEC=180°﹣∠AED,
∴∠ACB=∠AED.
由外角定理可得∠AED=∠ACD+∠CAE,
又∠ACB=∠ACD+∠BCF,
∴∠CAE=∠BCF,
由三角形内角和定理可得∠FBC=∠ECA.
②△FBC与△ECA全等,理由如下:
在△FBC和△ECA中,
,
∴△FBC≌△ECA(ASA).
(2)由(1)中②可知,FC=AE=11,BF=CE,
又EF=8,
∴CE=FC﹣EF=11﹣8=3,
∴BF=3,
故答案为:3.
(3)由(1)中结论可知S△FBC=S△ECA,
∴S△ECA+S△BDF=12=S△FBC+S△BDF=S△DBC,
又AB=4BD,
∴S△DBCS△ABC=12,
∴S△ABC=48.
故答案为:48.
26.(2020 岱岳区一模)已知∠ABC=90°,点D是直线AB边上的点,AD=BC.
(1)如图1,点D在线段AB上,过点A作AF⊥AB,且AF=BD,连接DC、DF、CF,试判断△CDF的形状并说明理由;
(2)如图2,点D在线段AB的延长线上,点F在点A的左侧,其他条件不变,以上结论是否仍然成立?请说明理由.
【解题思路】(1)利用SAS证明△FAD≌△DBC,再利用全等三角形的性质得出FD=DC,即可判断三角形的形状;
(2)利用SAS证明△FAD和△DBC全等,再利用全等三角形的性质得出FD=DC,∠FDC=90°,即可得出结论.
【解答过程】(1)△CDF是等腰直角三角形,
理由如下:
∵AF⊥AB,
∴∠A=90°,
在△FAD和△DBC中,
∵,
∴△FAD≌△DBC(SAS),
∴∠ADF=∠BCD,DF=DC,
∵∠BDC+∠BCD=90°,
∴∠ADF+∠CDB=90°,
∴∠FDC=180°﹣90°=90°,
又∵DF=DC,
∴△CDF是等腰直角三角形;
(2)仍然成立,
理由如下:
∵AF⊥AB,
∴∠A=90°,
在△FAD和△DBC中,
∵,
∴△FAD≌△DBC(SAS),
∴∠ADF=∠BCD,DF=DC,
∵∠BDC+∠BCD=90°,
∴∠ADF+∠BDC=90°,即∠FDC=90°,
又∵DF=DC,
∴△CDF是等腰直角三角形.
27.如图(1),线段AD∥BC,连接AB、CD,取CD中点E,连接AE,AE平分∠BAD.
(1)线段AB与AD、BC之间存在怎样的等量关系?请说明理由.
(2)如果点C在AB的左侧,其他条件不变,如图(2)所示,那么(1)中的结论还成立吗?如果成立,请说明理由;如果不成立,请写出新的结论,并说明理由.
【解题思路】(1)延长AE,BF交于点F,即可求证△ADE≌△FCE,即可求得CF=AD,AB=BF,即可求得AB=AD+BC;
(2)不成立,新的结论为:AB+BC=AD.延长AE,BF交于点F,可证△ADE≌△FCE和AB=BF,即可解题.
【解答过程】解:(1)延长AE,BF交于点F,
∵AE平分∠BAD,
∴∠BAF=∠DAF,
∵AD∥BC,
∴∠AFB=∠DAF,
∴AB=BF,
在△ADE和△FCE中,
,
∴△ADE≌△FCE(AAS),
∴CF=AD,
∵BF=BC+CF,
∴AB=BC+AD;
(2)不成立,新结论为:AB=AD﹣BC.
延长AE,BF交于点F,
证明:∵AE平分∠BAD,
∴∠BAF=∠DAF,
∵AD∥BC,
∴∠AFB=∠DAF,
∴AB=BF,
在△ADE和△FCE中,
,
∴△ADE≌△FCE(AAS),
∴CF=AD,
∵BF+BC=CF,
∴AB+BC=AD.
28.(2021春 章丘区期末)如图,CD是经过∠BCA顶点C的一条直线,CA=CB,E、F分别是直线CD上两点,且∠BEC=∠CFA=α.
(1)若直线CD经过∠BCA的内部,且E、F在射线CD上.
①如图1,若∠BCA=90°,α=90°,则BE = CF;
②如图2,若0°<∠BCA<180°,请添加一个关于α与∠BCA关系的条件 α+∠BCA=180° ,使①中的结论们然成立,并说明明理由;
(2)如图3,若线CD经过∠BCA的外部,a=∠BCA,请提出关于EF,BE,AF三条线段数量关系的合理猜想,并简述理由.
【解题思路】(1)由∠BCA=90°,∠BEC=∠CFA=α=90°,可得∠CBE=∠ACF,从而可证△BCE≌△CAF,故BE=CF.
(2)若BE=CF,则可使得△BCE≌△CAF.根据题目已知条件添加条件,再使得一对角相等,△BCE≌△CAF便可得证.
(3)题干已知条件可证△BCE≌△CAF,故BE=CF,EC=FA,从而可证明EF=BE+AF.
【解答过程】解:(1)∵∠BEC=∠CFA=α=90°,
∴∠BCE+∠CBE=180°﹣∠BEC=90°.
又∵∠BCA=∠BCE+∠ACF=90°,
∴∠CBE=∠ACF.
在△BCE和△CAF中,
∴△BCE≌△CAF(AAS).
∴BE=CF.
(2)α+∠BCA=180°,理由如下:
∵∠BEC=∠CFA=α,
∴∠BEF=180°﹣∠BEC=180°﹣α.
又∵∠BEF=∠EBC+∠BCE,
∴∠EBC+∠BCE=180°﹣α.
又∵α+∠BCA=180°,
∴∠BCA=180°﹣α.
∴∠BCA=∠BCE+∠ACF=180°﹣α.
∴∠EBC=∠FCA.
在△BCE和△CAF中,
∴△BCE≌△CAF(AAS).
∴BE=CF.
(3)EF=BE+AF,理由如下:
∵∠BCA=α,
∴∠BCE+∠ACF=180°﹣∠BCA=180°﹣α.
又∵∠BEC=α,
∴∠EBC+∠BCE=180°﹣∠BEC=180°﹣α.
∴∠EBC=∠FCA.
在△BEC和△CFA中,
∴△BEC≌△CFA(AAS).
∴BE=CF,EC=FA.
∴EF=EC+CF=FA+BE,即EF=BE+AF.
29.(2020春 南岸区期末)在∠MAN内有一点D,过点D分别作DB⊥AM,DC⊥AN,垂足分别为B,C.且BD=CD,点E,F分别在边AM和AN上.
(1)如图1,若∠BED=∠CFD,请说明DE=DF;
(2)如图2,若∠BDC=120°,∠EDF=60°,猜想EF,BE,CF具有的数量关系,并说明你的结论成立的理由.
【解题思路】(1)根据题目中的条件和∠BED=∠CFD,可以证明△BDE≌△CDF,从而可以得到DE=DF;
(2)作辅助线,过点D作∠CDG=∠BDE,交AN于点G,从而可以得到△BDE≌△CDG,然后即可得到DE=DG,BE=CG,再根据题目中的条件可以得到△EDF≌△GDF,即可得到EF=GF,然后即可得到EF,BE,CF具有的数量关系.
【解答过程】解:(1)∵DB⊥AM,DC⊥AN,
∴∠DBE=∠DCF=90°,
在△BDE和△CDF中,
∵
∴△BDE≌△CDF(AAS).
∴DE=DF;
(2)EF=FC+BE,
理由:过点D作∠CDG=∠BDE,交AN于点G,
在△BDE和△CDG中,
,
∴△BDE≌△CDG(ASA),
∴DE=DG,BE=CG.
∵∠BDC=120°,∠EDF=60°,
∴∠BDE+∠CDF=60°.
∴∠FDG=∠CDG+∠CDF=60°,
∴∠EDF=∠GDF.
在△EDF和△GDF中,
,
∴△EDF≌△GDF(SAS).
∴EF=GF,
∴EF=FC+CG=FC+BE.
30.(2021春 揭东区期末)已知点C为线段AB上一点,分别以AC、BC为边在线段AB同侧作△ACD和△BCE,且CA=CD,CB=CE,∠ACD=∠BCE,直线AE与BD交于点F.
(1)如图1,求证:△ACE≌△DCB.
(2)如图1,若∠ACD=60°,则∠AFB= 120° ;如图2,若∠ACD=90°,则∠AFB= 90° ;
(3)如图3,若∠ACD=β,则∠AFB= 180°﹣β (用含β的式子表示)并说明理由.
【解题思路】(1)求出∠ACE=∠DCB,根据SAS证出两三角形全等即可;
(2)根据全等三角形性质得出∠AEC=∠DBC,∠CDB=∠CAE,求出∠EAB+∠DBA=∠ACD,∠AFB=180°﹣(∠EAB+∠DBC),代入求出即可;
(3)根据全等三角形性质得出∠AEC=∠DBC,∠CDB=∠CAE,求出∠EAB+∠DBA=∠ACD,∠AFB=180°﹣(∠EAB+∠DBC),代入求出即可.
【解答过程】(1)证明:∵∠ACD=∠BCE,
∴∠ACD+∠DCE=∠BCE+∠DCE,
∴∠ACE=∠DCB,
在△ACE和△DCB中
∵,
∴△ACE≌△DCB;
(2)解:∵∠ACD=60°,
∴∠CDB+∠DBC=∠ACD=60°,
∵△ACE≌△DCB,
∴∠AEC=∠DBC,∠CDB=∠CAE,
∴∠CAE+∠DBC=60°,
∴∠AFB=180°﹣60°=120°;
当∠ACD=90°时,
∵∠ACD=90°,
∴∠CDB+∠DBC=∠ACD=90°,
∵△ACE≌△DCB,
∴∠AEC=∠DBC,∠CDB=∠CAE,
∴∠CAE+∠DBC=90°,
∴∠AFB=180°﹣90°=90°;
故答案为:120°,90°;
(3)解:当∠ACD=β时,∠AFB=180°﹣β,理由是:
∵∠ACD=β,
∴∠CDB+∠DBC=∠ACD=β,
∵△ACE≌△DCB,
∴∠AEC=∠DBC,∠CDB=∠CAE,
∴∠CAE+∠DBC=β,
∴∠AFB=180°﹣(∠CAE+∠DBC)=180°﹣β;
故答案为:180°﹣β.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
