第1章三角形的初步知识章末测试卷(A)(含答案)
文档属性
| 名称 | 第1章三角形的初步知识章末测试卷(A)(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-19 14:21:08 | ||
图片预览



文档简介
第1章三角形的初步知识章末测试卷(A)
考试时间:60分钟;满分:100分
姓名:___________班级:___________考号:___________
考卷信息:
本卷试题共23题,单选10题,填空6题,解答7题,满分100分,限时60分钟,本卷题型针对性较高,覆盖面广,选题有深度,可衡量学生掌握本章内容的具体情况!
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)(2021春 昌图县期末)根据下列已知条件,能唯一画出△ABC的是( )
A.∠C=90°,AB=6 B.AB=4,BC=3,∠A=30°
C.AB=5,BC=3 D.∠A=60°,∠B=45°,BC=4
2.(3分)(2021春 迁安市期末)如图,为估计池塘岸边A、B的距离,小方在池塘的一侧选取一点O,测得OA=10米,OB=8米,A、B间的距离不可能是( )
A.20米 B.16米 C.14米 D.10米
3.(3分)(2021春 砀山县期末)一块三角形玻璃样板不慎被张字同学碰破,成了四片完整碎片(如图所示),聪明的他经过仔细地考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板,你认为下列四个答案中考虑最全面的是( )
A.带1,2或2,3去就可以了
B.带1,4或3,4去就可以了
C.带1,4或2,4或3,4去均可
D.带其中的任意两块去都可以
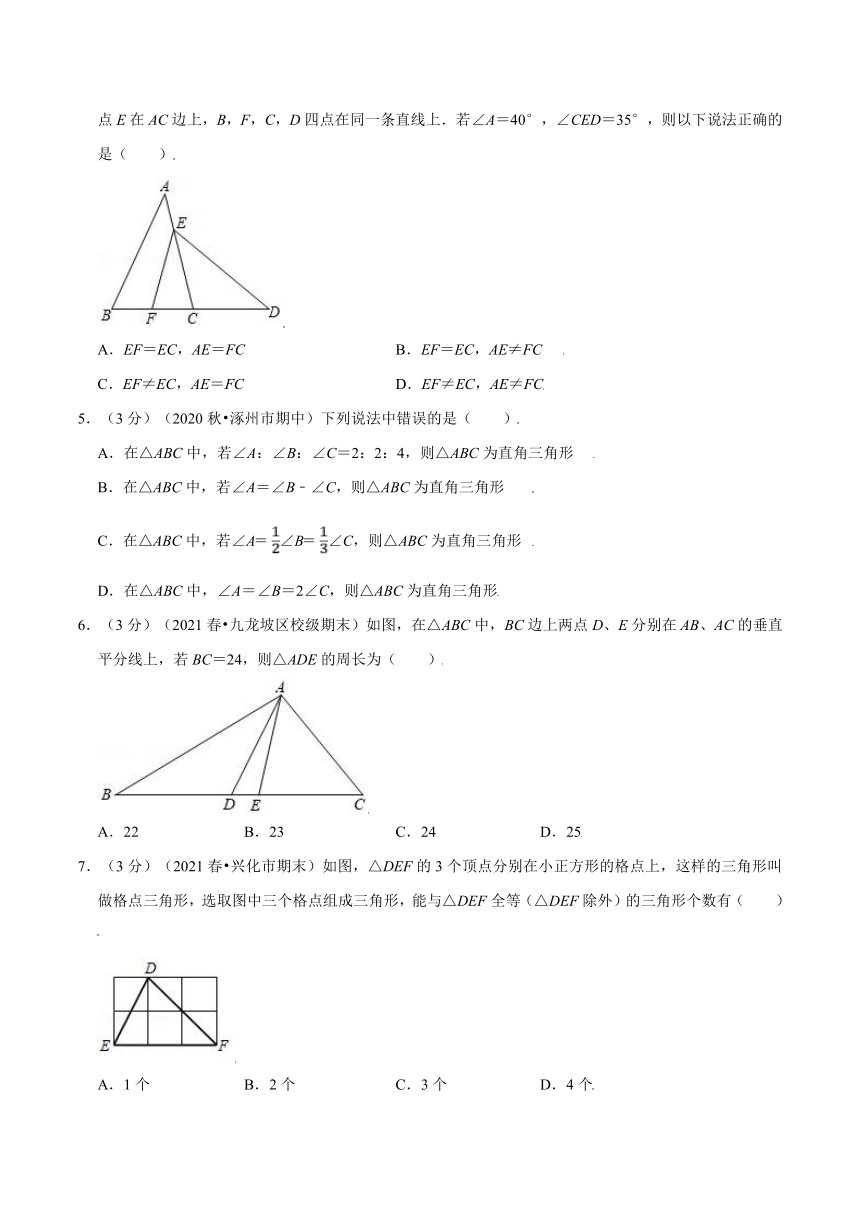
4.(3分)(2021春 海淀区校级月考)已知△ABC与△DEF全等,点A,B,C的对应点分别为D,E,F,点E在AC边上,B,F,C,D四点在同一条直线上.若∠A=40°,∠CED=35°,则以下说法正确的是( )
A.EF=EC,AE=FC B.EF=EC,AE≠FC
C.EF≠EC,AE=FC D.EF≠EC,AE≠FC
5.(3分)(2020秋 涿州市期中)下列说法中错误的是( )
A.在△ABC中,若∠A:∠B:∠C=2:2:4,则△ABC为直角三角形
B.在△ABC中,若∠A=∠B﹣∠C,则△ABC为直角三角形
C.在△ABC中,若∠A∠B∠C,则△ABC为直角三角形
D.在△ABC中,∠A=∠B=2∠C,则△ABC为直角三角形
6.(3分)(2021春 九龙坡区校级期末)如图,在△ABC中,BC边上两点D、E分别在AB、AC的垂直平分线上,若BC=24,则△ADE的周长为( )
A.22 B.23 C.24 D.25
7.(3分)(2021春 兴化市期末)如图,△DEF的3个顶点分别在小正方形的格点上,这样的三角形叫做格点三角形,选取图中三个格点组成三角形,能与△DEF全等(△DEF除外)的三角形个数有( )
A.1个 B.2个 C.3个 D.4个
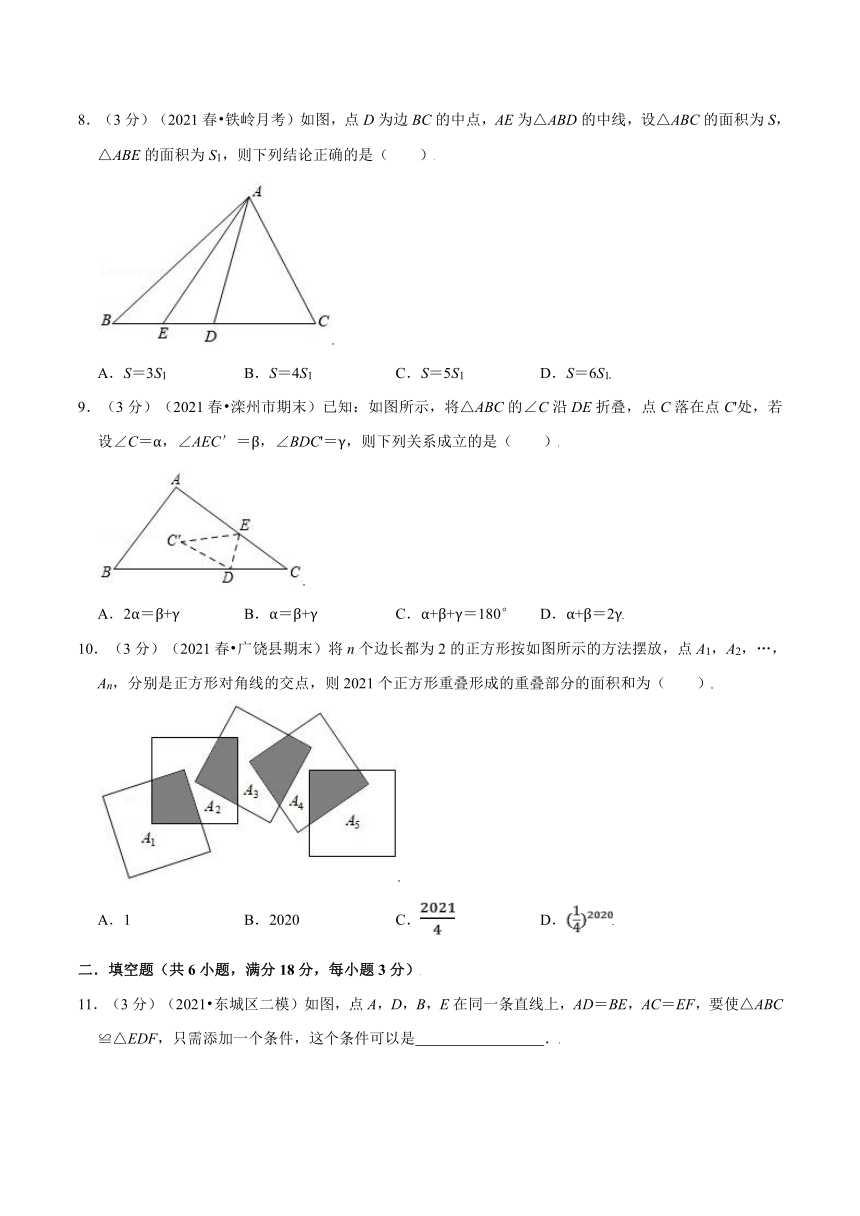
8.(3分)(2021春 铁岭月考)如图,点D为边BC的中点,AE为△ABD的中线,设△ABC的面积为S,△ABE的面积为S1,则下列结论正确的是( )
A.S=3S1 B.S=4S1 C.S=5S1 D.S=6S1
9.(3分)(2021春 滦州市期末)已知:如图所示,将△ABC的∠C沿DE折叠,点C落在点C'处,若设∠C=α,∠AEC′=β,∠BDC'=γ,则下列关系成立的是( )
A.2α=β+γ B.α=β+γ C.α+β+γ=180° D.α+β=2γ
10.(3分)(2021春 广饶县期末)将n个边长都为2的正方形按如图所示的方法摆放,点A1,A2,…,An,分别是正方形对角线的交点,则2021个正方形重叠形成的重叠部分的面积和为( )
A.1 B.2020 C. D.
二.填空题(共6小题,满分18分,每小题3分)
11.(3分)(2021 东城区二模)如图,点A,D,B,E在同一条直线上,AD=BE,AC=EF,要使△ABC≌△EDF,只需添加一个条件,这个条件可以是 .
12.(3分)(2021春 太康县期末)设a、b、c是△ABC的三边,化简:|a+b﹣c|﹣|b﹣c﹣a|= .
13.(3分)(2021春 玉田县期末)如图,△ABC中,AB=15,BC=9,BD是AC边上的中线,若△ABD的周长为30,则△BCD的周长是 .
14.(3分)(2021春 南岗区校级月考)如图,在△ABC中,∠C=90°,DE⊥AB于D,交AC于点E,若BC=BD,AC=6cm,BC=8cm,AB=10cm,则△ADE的周长是 .
15.(3分)(2021春 开江县期末)当三角形中的一个内角α是另一个内角β的二倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”有一个角是60°三角形,则这个三角形的其他两个角的度数为 .
16.(3分)(2021春 南召县期末)如图,在△ABC中,∠A=α,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A2020BC和∠A2020CD的平分线交于点A2021,则∠A2021= .
三.解答题(共7小题,满分52分)
17.(6分)(2021 碑林区校级模拟)如图,已知直线l外有一点P,请用尺规作图的方法在直线l上找一点Q,使得Q到P的距离最小(保留作图痕迹,不写作法).
18.(6分)在△ABC中,∠BAC=90°,AD⊥BC于D,CF是∠ACB的平分线,交AD于E,交AB于F,求证:∠AEF=∠AFE.
19.(8分)(2021春 长春期末)如图,点A、B分别在射线OM、ON上运动(不与点O重合),AC、BC分别是∠BAO和∠ABO的角平分线,BC延长线交OM于点G.
解决问题:
(1)若∠OBA=80°,∠OAB=40°,则∠ACG= ;(直接写出答案)
(2)若∠MON=100°,求出∠ACG的度数.
20.(8分)(2020秋 拱墅区期末)如图,AC与BD相交于点O,且OA=OC,OB=OD.
(1)求证:AB∥CD;
(2)直线EF过点O,分别交AB,CD于点E,F,试判断OE与OF是否相等,并说明理由.
21.(8分)(2021春 汉台区期末)如图:小刚站在河边的A点处,在河的对面(小刚的正北方向)的B处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树C处,接着再向前走了30步到达D处,然后他左转90°直行,当小刚看到电线塔、树与自己现处的位置E在一条直线时,他共走了140步.
(1)根据题意,画出示意图;
(2)如果小刚一步大约0.5米,估计小刚在点A处时他与电线塔的距离、并说明理由.
22.(8分)(2021春 亭湖区校级期末)如图,△ABC中,CD⊥AB,垂足为D.BE⊥AC,垂足为G,AB=CF,BE=AC.
(1)求证:AE=AF;
(2)AE与AF有何位置关系.请说明理由.
23.(8分)(2021春 佛山月考)在△ABC中,AB=AC,点D是射线CB上的一动点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段CB上,且∠BAC=90°时,那么∠DCE= 度;
(2)设∠BAC=α,∠DCE=β.
①如图2,当点D在线段CB上,∠BAC≠90°时,请你探究α与β之间的数量关系,并证明你的结论;
②如图3,当点D在线段CB的延长线上,∠BAC≠90°时,请将图3补充完整,写出此时α与β之间的数量关系并证明.
第1章三角形的初步知识章末测试卷(A)
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)(2021春 昌图县期末)根据下列已知条件,能唯一画出△ABC的是( )
A.∠C=90°,AB=6 B.AB=4,BC=3,∠A=30°
C.AB=5,BC=3 D.∠A=60°,∠B=45°,BC=4
【解题思路】根据全等三角形的判定方法对各选项进行判断.
【解答过程】解:A、当∠C=90°,AB=6,可根据全等三角形的判定方法判断三角形不唯一,所以A选项不符合题意;
B、当AB=6,BC=3,∠A=30°,可根据全等三角形的判定方法判断三角形不唯一,所以B选项不符合题意;
C、当AB=6,BC=3,可根据全等三角形的判定方法,判断三角形不唯一,所以C选项不符合题意;
D、当∠A=60°,∠B=45°,BC=4,可根据全等三角形的判定方法判断三角形唯一,所以D选项符合题意.
故选:D.
2.(3分)(2021春 迁安市期末)如图,为估计池塘岸边A、B的距离,小方在池塘的一侧选取一点O,测得OA=10米,OB=8米,A、B间的距离不可能是( )
A.20米 B.16米 C.14米 D.10米
【解题思路】根据三角形的三边关系,第三边的长一定大于已知的两边的差,而小于两边的和,求得相应范围,看哪个数值不在范围即可.
【解答过程】解:∵10﹣8<AB<10+8,
∴2<AB<18,
∴不可能是20米.
故选:A.
3.(3分)(2021春 砀山县期末)一块三角形玻璃样板不慎被张字同学碰破,成了四片完整碎片(如图所示),聪明的他经过仔细地考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板,你认为下列四个答案中考虑最全面的是( )
A.带1,2或2,3去就可以了
B.带1,4或3,4去就可以了
C.带1,4或2,4或3,4去均可
D.带其中的任意两块去都可以
【解题思路】2、4虽没有原三角形完整的边,又没有角,但延长可得出原三角形的形状;带1、4可以用“角边角”确定三角形;带3、4也可以用“角边角”确定三角形.
【解答过程】解:带3、4可以用“角边角”确定三角形,
带1、4可以用“角边角”确定三角形,
带2、4可以延长还原出原三角形,
故选:C.
4.(3分)(2021春 海淀区校级月考)已知△ABC与△DEF全等,点A,B,C的对应点分别为D,E,F,点E在AC边上,B,F,C,D四点在同一条直线上.若∠A=40°,∠CED=35°,则以下说法正确的是( )
A.EF=EC,AE=FC B.EF=EC,AE≠FC
C.EF≠EC,AE=FC D.EF≠EC,AE≠FC
【解题思路】根据全等三角形的性质得出对应边相等好对应角相等解答即可.
【解答过程】解:∵△ABC≌△DEF,
∴AB=DE,BC=EF,AC=DF,∠A=∠D,∠B=∠DEF,∠ACB=∠DFE,
∵∠A=40°,∠CED=35°,
∴∠D=40°,
∴∠ACB=40°+35°=75°,
∴∠B=180°﹣40°﹣75°=65°,
∴∠EFD=∠BCA=75°,
∴EF=EC,
∴BC=EF=EC,
∴得不出AE=FC,
故选:B.
5.(3分)(2020秋 涿州市期中)下列说法中错误的是( )
A.在△ABC中,若∠A:∠B:∠C=2:2:4,则△ABC为直角三角形
B.在△ABC中,若∠A=∠B﹣∠C,则△ABC为直角三角形
C.在△ABC中,若∠A∠B∠C,则△ABC为直角三角形
D.在△ABC中,∠A=∠B=2∠C,则△ABC为直角三角形
【解题思路】根据三角形内角和定理求出三角形的三个内角即可判断.
【解答过程】解:A、在△ABC中,因为∠A:∠B:∠C=2:2:4,所以∠C=90°,∠A=∠B=45°,△ABC为直角三角形,本选项不符合题意.
B、在△ABC中,因为∠A=∠B﹣∠C,所以∠B=90°,△ABC为直角三角形,本选项不符合题意.
C、在△ABC中,因为∠A∠B∠C,所以∠C=90°,∠B=60°,∠A=30°,△ABC为直角三角形,本选项不符合题意.
D、在△ABC中,因为∠A=∠B=2∠C,所以∠A=∠B=72°,∠C=36°,△ABC不是直角三角形,本选项符合题意,
故选:D.
6.(3分)(2021春 九龙坡区校级期末)如图,在△ABC中,BC边上两点D、E分别在AB、AC的垂直平分线上,若BC=24,则△ADE的周长为( )
A.22 B.23 C.24 D.25
【解题思路】根据线段垂直平分线的性质得到DA=DB,EA=EC,根据三角形的周长公式计算,得到答案.
【解答过程】解:∵点D、E分别在AB、AC的垂直平分线上,
∴DA=DB,EA=EC,
∴△ADE的周长=DA+DE+EA=DB+DE+EC=BC=24,
故选:C.
7.(3分)(2021春 兴化市期末)如图,△DEF的3个顶点分别在小正方形的格点上,这样的三角形叫做格点三角形,选取图中三个格点组成三角形,能与△DEF全等(△DEF除外)的三角形个数有( )
A.1个 B.2个 C.3个 D.4个
【解题思路】先根据全等三角形的判定定理画出图形,再得出选项即可.
【解答过程】解:如图所示:
能与△DEF全等(△DEF除外)的三角形有△ABC,△AGB,△HEF,共3个,
故选:C.
8.(3分)(2021春 铁岭月考)如图,点D为边BC的中点,AE为△ABD的中线,设△ABC的面积为S,△ABE的面积为S1,则下列结论正确的是( )
A.S=3S1 B.S=4S1 C.S=5S1 D.S=6S1
【解题思路】根据三角形中线的性质即可证明S△ADB=S△ADC;由此解答即可.
【解答过程】解:作AF⊥BC.
∵S△ADB=BD×AF,
S△ADC=CD×AFS,
又∵AD为△ABC中BC边上的中线,
∴BD=CD,
∴S△ADB=S△ADC,
同理,
∴S△ABES△ABC,
即S1S,
∴S=4S1,
故选:B.
9.(3分)(2021春 滦州市期末)已知:如图所示,将△ABC的∠C沿DE折叠,点C落在点C'处,若设∠C=α,∠AEC′=β,∠BDC'=γ,则下列关系成立的是( )
A.2α=β+γ B.α=β+γ C.α+β+γ=180° D.α+β=2γ
【解题思路】通过平角关系用∠CEC′、∠CDC′表示出β、γ,通过三角形的内角和用∠CEC′、∠CDC′表示出∠C、∠C′,计算可得结论.
【解答过程】解:由折叠的性质知:∠C=∠C′=α.
∵∠AEC′+∠CEC′=180°,∠BDC′+∠CDC′=180°,
∴β=180°﹣∠CEC′,γ=180°﹣∠CDC′.
∴β+γ=360°﹣∠CEC′﹣∠CDC′.
∵∠C+∠CEC′+CDC′+∠C′=360°,
∴2α=360°﹣∠CEC′﹣CDC′.
∴β+γ=2α.
故选:A.
10.(3分)(2021春 广饶县期末)将n个边长都为2的正方形按如图所示的方法摆放,点A1,A2,…,An,分别是正方形对角线的交点,则2021个正方形重叠形成的重叠部分的面积和为( )
A.1 B.2020 C. D.
【解题思路】过正方形ABCD的中心O作OM⊥CD于M,作ON⊥BC于N,则易证△OEM≌△OFN,根据已知可求得一个阴影部分的面积是正方形的面积的,已知两个正方形可得到一个阴影部分,则n个这样的正方形重叠部分即为n﹣1阴影部分的和,即可得出结果.
【解答过程】解:如图,过正方形ABCD的中心O作OM⊥CD于M,作ON⊥BC于N,
则∠EOM=∠FON,OM=ON,且∠EMO=∠FNO=90°,
∴△OEM≌△OFN(ASA),
则四边形OECF的面积就等于正方形OMCN的面积,
则OMCN的面积是1,
∴得阴影部分面积等于正方形面积的,即是1,
∴则2021个正方形重叠形成的重叠部分的面积和=2020×1=2020cm2,
故选:B.
二.填空题(共6小题,满分18分,每小题3分)
11.(3分)(2021 东城区二模)如图,点A,D,B,E在同一条直线上,AD=BE,AC=EF,要使△ABC≌△EDF,只需添加一个条件,这个条件可以是 BC=DF(答案不唯一) .
【解题思路】根据全等三角形的判定方法可以由SSS证明△ABC≌△EDF.
【解答过程】解:添加BC=DF.
∵AD=BE,
∴AD+DB=BE+BD,
∴AB=ED,
在△ABC和△EDF中,
,
∴△ABC≌△EDF(SSS),
故答案为:BC=DF(答案不唯一).
12.(3分)(2021春 太康县期末)设a、b、c是△ABC的三边,化简:|a+b﹣c|﹣|b﹣c﹣a|= 2b﹣2c .
【解题思路】根据三角形的任意两边之和大于第三边可得a+b﹣c>0,b﹣c﹣a<0,再根据绝对值的性质去掉绝对值符号,然后利用整式的加减运算进行计算即可得解.
【解答过程】解:∵a、b、c分别为△ABC的三边长,
∴a+b﹣c>0,b﹣c﹣a<0,
∴|a+b﹣c|﹣|b﹣c﹣a|
=a+b﹣c+b﹣c﹣a
=2b﹣2c,
故答案为:2b﹣2c.
13.(3分)(2021春 玉田县期末)如图,△ABC中,AB=15,BC=9,BD是AC边上的中线,若△ABD的周长为30,则△BCD的周长是 24 .
【解题思路】根据三角形中线的定义可得AD=CD,由△ABD的周长为30,AB=15,求出AD+BD=15,进而得出△BCD的周长.
【解答过程】解:∵BD是AC边上的中线,
∴AD=CD,
∵△ABD的周长为30,AB=15,
∴AD+BD=30﹣AB=30﹣15=15,
∴CD+BD=AD+BD=15,
∵BC=9,
∴△BCD的周长=BC+CD+BD=9+15=24.
故答案为:24.
14.(3分)(2021春 南岗区校级月考)如图,在△ABC中,∠C=90°,DE⊥AB于D,交AC于点E,若BC=BD,AC=6cm,BC=8cm,AB=10cm,则△ADE的周长是 8cm .
【解题思路】连接BE,利用HL证明Rt△BCE与Rt△BDE全等,利用全等三角形的性质解答即可.
【解答过程】解:连接BE,
∵∠C=90°,DE⊥AB于D,
∴∠C=∠BDE=90°,
在Rt△BCE与Rt△BDE中,
,
∴Rt△BCE≌Rt△BDE(HL),
∴DE=CE,
∵AB=10cm,BC=8cm,AC=6cm,
∴△ADE的周长=DE+AE+AD=CE+AE+AB﹣BD=AC+AB﹣BC=6+10﹣8=8(cm),
故答案为:8cm.
15.(3分)(2021春 开江县期末)当三角形中的一个内角α是另一个内角β的二倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”有一个角是60°三角形,则这个三角形的其他两个角的度数为 30°,90°或40°,80° .
【解题思路】可分三种情况:当α=60°时,β=30°,当β=60°时,α=120°,当第三个角为60°时,利用三角形的内角和定理分别进行计算,可求解.
【解答过程】解:当α=60°时,β=30°,
∴该“特征三角形”的第三个角为180°﹣60°﹣30°=90°;
即该三角形的其余两个角的度数为30°,90°;
当β=60°时,α=120°,此时三角形的第三个角为0°,该三角形不存在;
当第三个角为60°时,则α+β=180°﹣60°=120°,
∵α=2β,
∴α=80°,β=40°,
即该三角形的其余两个角的度数为40°,80°,
综上该三角形的其余两个角的度数分别为30°,90°或40°,80°.
故答案为30°,90°或40°,80°.
16.(3分)(2021春 南召县期末)如图,在△ABC中,∠A=α,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A2020BC和∠A2020CD的平分线交于点A2021,则∠A2021= .
【解题思路】根据题目,需运用特殊到一般的数学思想分析本题.由A1B平分∠ABC,A1C平分∠ACD,,.由三角形外角的性质,得∠A1CD=∠A1BC+∠A1,进而推断出∠A1=∠A1CD﹣∠A1BC.以此类推,可得出结论.
【解答过程】解:∵A1B平分∠ABC,A1C平分∠ACD,
∴,.
∵∠A1CD=∠A1BC+∠A1,
∴∠A1=∠A1CD﹣∠A1BC
.
同理可证,.
∴.
以此类推…
∴.
∵∠A=α,
∴.
故答案为:.
三.解答题(共7小题,满分52分)
17.(6分)(2021 碑林区校级模拟)如图,已知直线l外有一点P,请用尺规作图的方法在直线l上找一点Q,使得Q到P的距离最小(保留作图痕迹,不写作法).
【解题思路】根据垂线段最短,作PQ⊥直线l于Q即可.
【解答过程】解:如图,线段PQ即为所求.
18.(6分)在△ABC中,∠BAC=90°,AD⊥BC于D,CF是∠ACB的平分线,交AD于E,交AB于F,求证:∠AEF=∠AFE.
【解题思路】根据角平分线的定义可得∠ACF=∠BCF,再根据直角三角形两锐角互余可得∠ACF+∠AFE=90°,∠BCF+∠CED=90°,然后得到∠AFE=∠CED,根据对顶角相等可得∠AEF=∠CED,从而得证.
【解答过程】证明:∵CF是∠ACB的平分线,
∴∠ACF=∠BCF,
∵∠BAC=90°,AD⊥BC,
∴∠ACF+∠AFE=90°,∠BCF+∠CED=90°,
∴∠AFE=∠CED,
∵∠AEF=∠CED(对顶角相等),
∴∠AEF=∠AFE.
19.(8分)(2021春 长春期末)如图,点A、B分别在射线OM、ON上运动(不与点O重合),AC、BC分别是∠BAO和∠ABO的角平分线,BC延长线交OM于点G.
解决问题:
(1)若∠OBA=80°,∠OAB=40°,则∠ACG= 60° ;(直接写出答案)
(2)若∠MON=100°,求出∠ACG的度数.
【解题思路】(1)由角平分线的定义可求出∠CBA和∠CAB的度数,再根据三角形外角的性质求出∠ACG的度数即可;
(2)先根据三角形内角和定理求出∠OBA+∠OAB的度数,然后再根据角平分线的定义求出∠CBA+∠CAB的度数,最后根据三角形外角的性质求出结果即可.
【解答过程】解:(1)∵AC、BC分别是∠BAO和∠ABO的角平分线,
∴∠CBA∠ABO,∠CAB∠BAO,
∵∠OBA=80°,∠OAB=40°,
∴∠CBA=40°,∠CAB=20°,
∴∠ACG=∠CBA+∠CAB=60°.
故答案为:60°.
(2)∵∠MON=100°,
∴∠BAO+∠ABO=180°﹣100°=80°,
∵AC、BC分别是∠BAO和∠ABO的角平分线,
∴∠CBA∠ABO,∠CAB∠BAO,
∴∠CBA+∠CAB(∠ABO+∠BAO)80°=40°,
∴∠ACG=∠CBA+∠CAB=40°.
20.(8分)(2020秋 拱墅区期末)如图,AC与BD相交于点O,且OA=OC,OB=OD.
(1)求证:AB∥CD;
(2)直线EF过点O,分别交AB,CD于点E,F,试判断OE与OF是否相等,并说明理由.
【解题思路】(1)∠COD与∠AOB是对顶角,根据SAS可证明△OAB≌△OCD,由全等三角形的性质得到∠A=∠C,即可判定AB∥CD;
(2)在△OAB≌△OCD的基础上证明△EOB≌△FOD.再根据全等三角形的性质得OE=OF.
【解答过程】(1)证明:在△OAB与△OCD中,
,
∴△OAB≌△OCD(SAS),
∴∠A=∠C,
∴AB∥CD;
(2)解:OE=OF,理由如下:
由(1)知,△OAB≌△OCD,
∴∠B=∠D,OB=OD,
在△EOB与△FOD中
,
∴△EOB≌△FOD(ASA),
∴OE=OF.
21.(8分)(2021春 汉台区期末)如图:小刚站在河边的A点处,在河的对面(小刚的正北方向)的B处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树C处,接着再向前走了30步到达D处,然后他左转90°直行,当小刚看到电线塔、树与自己现处的位置E在一条直线时,他共走了140步.
(1)根据题意,画出示意图;
(2)如果小刚一步大约0.5米,估计小刚在点A处时他与电线塔的距离、并说明理由.
【解题思路】(1)根据题意画出图形即可;
(2)根据AAS可得出△ABC≌△DEC,由该全等三角形的性质AB=DE.
【解答过程】解:(1)如图所示;
(2)由题意得,DE=140﹣30﹣30=80(步),
在△ABC和△DEC中,
,
∴△ABC≌△DEC(ASA),
∴AB=DE,
又∵小刚走完DE用来80步,一步大约0.5米,
∴DE=80×0.5=40(米).
答:小刚在点A处时他与电线塔的距离为40米.
22.(8分)(2021春 亭湖区校级期末)如图,△ABC中,CD⊥AB,垂足为D.BE⊥AC,垂足为G,AB=CF,BE=AC.
(1)求证:AE=AF;
(2)AE与AF有何位置关系.请说明理由.
【解题思路】(1)利用SAS证明△AEB≌△FAC可证明结论;
(2)由全等三角形的性质可得∠E=∠CAF,由余角的定义可求得∠EAF的度数即可得解.
【解答过程】(1)证明:∵CD⊥AB,BE⊥AC,
∴∠ADC=∠AGB=90°,
∴∠CAD+∠ACD=∠CAD+∠EBA=90°,
∴∠ACD=∠EBA,
在△AEB和△FAC中,
,
∴△AEB≌△FAC(SAS),
∴AE=AF;
(2)解:AE⊥AF,理由如下:
由(1)知△AEB≌△FAC,
∴∠E=∠CAF,
∵BE⊥AC,垂足为G,
∴∠AGE=90°,
∵∠E+∠EAG=90°,
∴∠CAF+∠EAG=90°,
即∠EAF=90°,
∴AE⊥AF.
23.(8分)(2021春 佛山月考)在△ABC中,AB=AC,点D是射线CB上的一动点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段CB上,且∠BAC=90°时,那么∠DCE= 90 度;
(2)设∠BAC=α,∠DCE=β.
①如图2,当点D在线段CB上,∠BAC≠90°时,请你探究α与β之间的数量关系,并证明你的结论;
②如图3,当点D在线段CB的延长线上,∠BAC≠90°时,请将图3补充完整,写出此时α与β之间的数量关系并证明.
【解题思路】(1)易证∠BAD=∠CAE,即可证明△BAD≌△CAE,可得∠ACE=∠B,即可解题;
(2)易证∠BAD=∠CAE,即可证明△BAD≌△CAE,可得∠ACE=∠B,根据∠B+∠ACB=180°﹣α即可解题;
(3)易证∠BAD=∠CAE,即可证明△BAD≌△CAE,可得∠ACE=∠B,根据∠ADE+∠AED+α=180°,∠CDE+∠CED+β=180°即可解题.
【解答过程】解:(1)∵∠BAD+∠DAC=90°,∠DAC+∠CAE=90°,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴∠ACE=∠B,
∵∠B+∠ACB=90°,
∴∠DCE=∠ACE+∠ACB=90°;
故答案为 90.
(2)∵∠BAD+∠DAC=α,∠DAC+∠CAE=α,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴∠ACE=∠B,
∵∠B+∠ACB=180°﹣α,
∴∠DCE=∠ACE+∠ACB=180°﹣α=β,
∴α+β=180°;
(3)作出图形,
∵∠BAD+∠BAE=α,∠BAE+∠CAE=α,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴∠AEC=∠ADB,
∵∠ADE+∠AED+α=180°,∠CDE+∠CED+β=180°,
∠CED=∠AEC+∠AED,
∴α=β.
考试时间:60分钟;满分:100分
姓名:___________班级:___________考号:___________
考卷信息:
本卷试题共23题,单选10题,填空6题,解答7题,满分100分,限时60分钟,本卷题型针对性较高,覆盖面广,选题有深度,可衡量学生掌握本章内容的具体情况!
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)(2021春 昌图县期末)根据下列已知条件,能唯一画出△ABC的是( )
A.∠C=90°,AB=6 B.AB=4,BC=3,∠A=30°
C.AB=5,BC=3 D.∠A=60°,∠B=45°,BC=4
2.(3分)(2021春 迁安市期末)如图,为估计池塘岸边A、B的距离,小方在池塘的一侧选取一点O,测得OA=10米,OB=8米,A、B间的距离不可能是( )
A.20米 B.16米 C.14米 D.10米
3.(3分)(2021春 砀山县期末)一块三角形玻璃样板不慎被张字同学碰破,成了四片完整碎片(如图所示),聪明的他经过仔细地考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板,你认为下列四个答案中考虑最全面的是( )
A.带1,2或2,3去就可以了
B.带1,4或3,4去就可以了
C.带1,4或2,4或3,4去均可
D.带其中的任意两块去都可以
4.(3分)(2021春 海淀区校级月考)已知△ABC与△DEF全等,点A,B,C的对应点分别为D,E,F,点E在AC边上,B,F,C,D四点在同一条直线上.若∠A=40°,∠CED=35°,则以下说法正确的是( )
A.EF=EC,AE=FC B.EF=EC,AE≠FC
C.EF≠EC,AE=FC D.EF≠EC,AE≠FC
5.(3分)(2020秋 涿州市期中)下列说法中错误的是( )
A.在△ABC中,若∠A:∠B:∠C=2:2:4,则△ABC为直角三角形
B.在△ABC中,若∠A=∠B﹣∠C,则△ABC为直角三角形
C.在△ABC中,若∠A∠B∠C,则△ABC为直角三角形
D.在△ABC中,∠A=∠B=2∠C,则△ABC为直角三角形
6.(3分)(2021春 九龙坡区校级期末)如图,在△ABC中,BC边上两点D、E分别在AB、AC的垂直平分线上,若BC=24,则△ADE的周长为( )
A.22 B.23 C.24 D.25
7.(3分)(2021春 兴化市期末)如图,△DEF的3个顶点分别在小正方形的格点上,这样的三角形叫做格点三角形,选取图中三个格点组成三角形,能与△DEF全等(△DEF除外)的三角形个数有( )
A.1个 B.2个 C.3个 D.4个
8.(3分)(2021春 铁岭月考)如图,点D为边BC的中点,AE为△ABD的中线,设△ABC的面积为S,△ABE的面积为S1,则下列结论正确的是( )
A.S=3S1 B.S=4S1 C.S=5S1 D.S=6S1
9.(3分)(2021春 滦州市期末)已知:如图所示,将△ABC的∠C沿DE折叠,点C落在点C'处,若设∠C=α,∠AEC′=β,∠BDC'=γ,则下列关系成立的是( )
A.2α=β+γ B.α=β+γ C.α+β+γ=180° D.α+β=2γ
10.(3分)(2021春 广饶县期末)将n个边长都为2的正方形按如图所示的方法摆放,点A1,A2,…,An,分别是正方形对角线的交点,则2021个正方形重叠形成的重叠部分的面积和为( )
A.1 B.2020 C. D.
二.填空题(共6小题,满分18分,每小题3分)
11.(3分)(2021 东城区二模)如图,点A,D,B,E在同一条直线上,AD=BE,AC=EF,要使△ABC≌△EDF,只需添加一个条件,这个条件可以是 .
12.(3分)(2021春 太康县期末)设a、b、c是△ABC的三边,化简:|a+b﹣c|﹣|b﹣c﹣a|= .
13.(3分)(2021春 玉田县期末)如图,△ABC中,AB=15,BC=9,BD是AC边上的中线,若△ABD的周长为30,则△BCD的周长是 .
14.(3分)(2021春 南岗区校级月考)如图,在△ABC中,∠C=90°,DE⊥AB于D,交AC于点E,若BC=BD,AC=6cm,BC=8cm,AB=10cm,则△ADE的周长是 .
15.(3分)(2021春 开江县期末)当三角形中的一个内角α是另一个内角β的二倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”有一个角是60°三角形,则这个三角形的其他两个角的度数为 .
16.(3分)(2021春 南召县期末)如图,在△ABC中,∠A=α,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A2020BC和∠A2020CD的平分线交于点A2021,则∠A2021= .
三.解答题(共7小题,满分52分)
17.(6分)(2021 碑林区校级模拟)如图,已知直线l外有一点P,请用尺规作图的方法在直线l上找一点Q,使得Q到P的距离最小(保留作图痕迹,不写作法).
18.(6分)在△ABC中,∠BAC=90°,AD⊥BC于D,CF是∠ACB的平分线,交AD于E,交AB于F,求证:∠AEF=∠AFE.
19.(8分)(2021春 长春期末)如图,点A、B分别在射线OM、ON上运动(不与点O重合),AC、BC分别是∠BAO和∠ABO的角平分线,BC延长线交OM于点G.
解决问题:
(1)若∠OBA=80°,∠OAB=40°,则∠ACG= ;(直接写出答案)
(2)若∠MON=100°,求出∠ACG的度数.
20.(8分)(2020秋 拱墅区期末)如图,AC与BD相交于点O,且OA=OC,OB=OD.
(1)求证:AB∥CD;
(2)直线EF过点O,分别交AB,CD于点E,F,试判断OE与OF是否相等,并说明理由.
21.(8分)(2021春 汉台区期末)如图:小刚站在河边的A点处,在河的对面(小刚的正北方向)的B处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树C处,接着再向前走了30步到达D处,然后他左转90°直行,当小刚看到电线塔、树与自己现处的位置E在一条直线时,他共走了140步.
(1)根据题意,画出示意图;
(2)如果小刚一步大约0.5米,估计小刚在点A处时他与电线塔的距离、并说明理由.
22.(8分)(2021春 亭湖区校级期末)如图,△ABC中,CD⊥AB,垂足为D.BE⊥AC,垂足为G,AB=CF,BE=AC.
(1)求证:AE=AF;
(2)AE与AF有何位置关系.请说明理由.
23.(8分)(2021春 佛山月考)在△ABC中,AB=AC,点D是射线CB上的一动点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段CB上,且∠BAC=90°时,那么∠DCE= 度;
(2)设∠BAC=α,∠DCE=β.
①如图2,当点D在线段CB上,∠BAC≠90°时,请你探究α与β之间的数量关系,并证明你的结论;
②如图3,当点D在线段CB的延长线上,∠BAC≠90°时,请将图3补充完整,写出此时α与β之间的数量关系并证明.
第1章三角形的初步知识章末测试卷(A)
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)(2021春 昌图县期末)根据下列已知条件,能唯一画出△ABC的是( )
A.∠C=90°,AB=6 B.AB=4,BC=3,∠A=30°
C.AB=5,BC=3 D.∠A=60°,∠B=45°,BC=4
【解题思路】根据全等三角形的判定方法对各选项进行判断.
【解答过程】解:A、当∠C=90°,AB=6,可根据全等三角形的判定方法判断三角形不唯一,所以A选项不符合题意;
B、当AB=6,BC=3,∠A=30°,可根据全等三角形的判定方法判断三角形不唯一,所以B选项不符合题意;
C、当AB=6,BC=3,可根据全等三角形的判定方法,判断三角形不唯一,所以C选项不符合题意;
D、当∠A=60°,∠B=45°,BC=4,可根据全等三角形的判定方法判断三角形唯一,所以D选项符合题意.
故选:D.
2.(3分)(2021春 迁安市期末)如图,为估计池塘岸边A、B的距离,小方在池塘的一侧选取一点O,测得OA=10米,OB=8米,A、B间的距离不可能是( )
A.20米 B.16米 C.14米 D.10米
【解题思路】根据三角形的三边关系,第三边的长一定大于已知的两边的差,而小于两边的和,求得相应范围,看哪个数值不在范围即可.
【解答过程】解:∵10﹣8<AB<10+8,
∴2<AB<18,
∴不可能是20米.
故选:A.
3.(3分)(2021春 砀山县期末)一块三角形玻璃样板不慎被张字同学碰破,成了四片完整碎片(如图所示),聪明的他经过仔细地考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板,你认为下列四个答案中考虑最全面的是( )
A.带1,2或2,3去就可以了
B.带1,4或3,4去就可以了
C.带1,4或2,4或3,4去均可
D.带其中的任意两块去都可以
【解题思路】2、4虽没有原三角形完整的边,又没有角,但延长可得出原三角形的形状;带1、4可以用“角边角”确定三角形;带3、4也可以用“角边角”确定三角形.
【解答过程】解:带3、4可以用“角边角”确定三角形,
带1、4可以用“角边角”确定三角形,
带2、4可以延长还原出原三角形,
故选:C.
4.(3分)(2021春 海淀区校级月考)已知△ABC与△DEF全等,点A,B,C的对应点分别为D,E,F,点E在AC边上,B,F,C,D四点在同一条直线上.若∠A=40°,∠CED=35°,则以下说法正确的是( )
A.EF=EC,AE=FC B.EF=EC,AE≠FC
C.EF≠EC,AE=FC D.EF≠EC,AE≠FC
【解题思路】根据全等三角形的性质得出对应边相等好对应角相等解答即可.
【解答过程】解:∵△ABC≌△DEF,
∴AB=DE,BC=EF,AC=DF,∠A=∠D,∠B=∠DEF,∠ACB=∠DFE,
∵∠A=40°,∠CED=35°,
∴∠D=40°,
∴∠ACB=40°+35°=75°,
∴∠B=180°﹣40°﹣75°=65°,
∴∠EFD=∠BCA=75°,
∴EF=EC,
∴BC=EF=EC,
∴得不出AE=FC,
故选:B.
5.(3分)(2020秋 涿州市期中)下列说法中错误的是( )
A.在△ABC中,若∠A:∠B:∠C=2:2:4,则△ABC为直角三角形
B.在△ABC中,若∠A=∠B﹣∠C,则△ABC为直角三角形
C.在△ABC中,若∠A∠B∠C,则△ABC为直角三角形
D.在△ABC中,∠A=∠B=2∠C,则△ABC为直角三角形
【解题思路】根据三角形内角和定理求出三角形的三个内角即可判断.
【解答过程】解:A、在△ABC中,因为∠A:∠B:∠C=2:2:4,所以∠C=90°,∠A=∠B=45°,△ABC为直角三角形,本选项不符合题意.
B、在△ABC中,因为∠A=∠B﹣∠C,所以∠B=90°,△ABC为直角三角形,本选项不符合题意.
C、在△ABC中,因为∠A∠B∠C,所以∠C=90°,∠B=60°,∠A=30°,△ABC为直角三角形,本选项不符合题意.
D、在△ABC中,因为∠A=∠B=2∠C,所以∠A=∠B=72°,∠C=36°,△ABC不是直角三角形,本选项符合题意,
故选:D.
6.(3分)(2021春 九龙坡区校级期末)如图,在△ABC中,BC边上两点D、E分别在AB、AC的垂直平分线上,若BC=24,则△ADE的周长为( )
A.22 B.23 C.24 D.25
【解题思路】根据线段垂直平分线的性质得到DA=DB,EA=EC,根据三角形的周长公式计算,得到答案.
【解答过程】解:∵点D、E分别在AB、AC的垂直平分线上,
∴DA=DB,EA=EC,
∴△ADE的周长=DA+DE+EA=DB+DE+EC=BC=24,
故选:C.
7.(3分)(2021春 兴化市期末)如图,△DEF的3个顶点分别在小正方形的格点上,这样的三角形叫做格点三角形,选取图中三个格点组成三角形,能与△DEF全等(△DEF除外)的三角形个数有( )
A.1个 B.2个 C.3个 D.4个
【解题思路】先根据全等三角形的判定定理画出图形,再得出选项即可.
【解答过程】解:如图所示:
能与△DEF全等(△DEF除外)的三角形有△ABC,△AGB,△HEF,共3个,
故选:C.
8.(3分)(2021春 铁岭月考)如图,点D为边BC的中点,AE为△ABD的中线,设△ABC的面积为S,△ABE的面积为S1,则下列结论正确的是( )
A.S=3S1 B.S=4S1 C.S=5S1 D.S=6S1
【解题思路】根据三角形中线的性质即可证明S△ADB=S△ADC;由此解答即可.
【解答过程】解:作AF⊥BC.
∵S△ADB=BD×AF,
S△ADC=CD×AFS,
又∵AD为△ABC中BC边上的中线,
∴BD=CD,
∴S△ADB=S△ADC,
同理,
∴S△ABES△ABC,
即S1S,
∴S=4S1,
故选:B.
9.(3分)(2021春 滦州市期末)已知:如图所示,将△ABC的∠C沿DE折叠,点C落在点C'处,若设∠C=α,∠AEC′=β,∠BDC'=γ,则下列关系成立的是( )
A.2α=β+γ B.α=β+γ C.α+β+γ=180° D.α+β=2γ
【解题思路】通过平角关系用∠CEC′、∠CDC′表示出β、γ,通过三角形的内角和用∠CEC′、∠CDC′表示出∠C、∠C′,计算可得结论.
【解答过程】解:由折叠的性质知:∠C=∠C′=α.
∵∠AEC′+∠CEC′=180°,∠BDC′+∠CDC′=180°,
∴β=180°﹣∠CEC′,γ=180°﹣∠CDC′.
∴β+γ=360°﹣∠CEC′﹣∠CDC′.
∵∠C+∠CEC′+CDC′+∠C′=360°,
∴2α=360°﹣∠CEC′﹣CDC′.
∴β+γ=2α.
故选:A.
10.(3分)(2021春 广饶县期末)将n个边长都为2的正方形按如图所示的方法摆放,点A1,A2,…,An,分别是正方形对角线的交点,则2021个正方形重叠形成的重叠部分的面积和为( )
A.1 B.2020 C. D.
【解题思路】过正方形ABCD的中心O作OM⊥CD于M,作ON⊥BC于N,则易证△OEM≌△OFN,根据已知可求得一个阴影部分的面积是正方形的面积的,已知两个正方形可得到一个阴影部分,则n个这样的正方形重叠部分即为n﹣1阴影部分的和,即可得出结果.
【解答过程】解:如图,过正方形ABCD的中心O作OM⊥CD于M,作ON⊥BC于N,
则∠EOM=∠FON,OM=ON,且∠EMO=∠FNO=90°,
∴△OEM≌△OFN(ASA),
则四边形OECF的面积就等于正方形OMCN的面积,
则OMCN的面积是1,
∴得阴影部分面积等于正方形面积的,即是1,
∴则2021个正方形重叠形成的重叠部分的面积和=2020×1=2020cm2,
故选:B.
二.填空题(共6小题,满分18分,每小题3分)
11.(3分)(2021 东城区二模)如图,点A,D,B,E在同一条直线上,AD=BE,AC=EF,要使△ABC≌△EDF,只需添加一个条件,这个条件可以是 BC=DF(答案不唯一) .
【解题思路】根据全等三角形的判定方法可以由SSS证明△ABC≌△EDF.
【解答过程】解:添加BC=DF.
∵AD=BE,
∴AD+DB=BE+BD,
∴AB=ED,
在△ABC和△EDF中,
,
∴△ABC≌△EDF(SSS),
故答案为:BC=DF(答案不唯一).
12.(3分)(2021春 太康县期末)设a、b、c是△ABC的三边,化简:|a+b﹣c|﹣|b﹣c﹣a|= 2b﹣2c .
【解题思路】根据三角形的任意两边之和大于第三边可得a+b﹣c>0,b﹣c﹣a<0,再根据绝对值的性质去掉绝对值符号,然后利用整式的加减运算进行计算即可得解.
【解答过程】解:∵a、b、c分别为△ABC的三边长,
∴a+b﹣c>0,b﹣c﹣a<0,
∴|a+b﹣c|﹣|b﹣c﹣a|
=a+b﹣c+b﹣c﹣a
=2b﹣2c,
故答案为:2b﹣2c.
13.(3分)(2021春 玉田县期末)如图,△ABC中,AB=15,BC=9,BD是AC边上的中线,若△ABD的周长为30,则△BCD的周长是 24 .
【解题思路】根据三角形中线的定义可得AD=CD,由△ABD的周长为30,AB=15,求出AD+BD=15,进而得出△BCD的周长.
【解答过程】解:∵BD是AC边上的中线,
∴AD=CD,
∵△ABD的周长为30,AB=15,
∴AD+BD=30﹣AB=30﹣15=15,
∴CD+BD=AD+BD=15,
∵BC=9,
∴△BCD的周长=BC+CD+BD=9+15=24.
故答案为:24.
14.(3分)(2021春 南岗区校级月考)如图,在△ABC中,∠C=90°,DE⊥AB于D,交AC于点E,若BC=BD,AC=6cm,BC=8cm,AB=10cm,则△ADE的周长是 8cm .
【解题思路】连接BE,利用HL证明Rt△BCE与Rt△BDE全等,利用全等三角形的性质解答即可.
【解答过程】解:连接BE,
∵∠C=90°,DE⊥AB于D,
∴∠C=∠BDE=90°,
在Rt△BCE与Rt△BDE中,
,
∴Rt△BCE≌Rt△BDE(HL),
∴DE=CE,
∵AB=10cm,BC=8cm,AC=6cm,
∴△ADE的周长=DE+AE+AD=CE+AE+AB﹣BD=AC+AB﹣BC=6+10﹣8=8(cm),
故答案为:8cm.
15.(3分)(2021春 开江县期末)当三角形中的一个内角α是另一个内角β的二倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”有一个角是60°三角形,则这个三角形的其他两个角的度数为 30°,90°或40°,80° .
【解题思路】可分三种情况:当α=60°时,β=30°,当β=60°时,α=120°,当第三个角为60°时,利用三角形的内角和定理分别进行计算,可求解.
【解答过程】解:当α=60°时,β=30°,
∴该“特征三角形”的第三个角为180°﹣60°﹣30°=90°;
即该三角形的其余两个角的度数为30°,90°;
当β=60°时,α=120°,此时三角形的第三个角为0°,该三角形不存在;
当第三个角为60°时,则α+β=180°﹣60°=120°,
∵α=2β,
∴α=80°,β=40°,
即该三角形的其余两个角的度数为40°,80°,
综上该三角形的其余两个角的度数分别为30°,90°或40°,80°.
故答案为30°,90°或40°,80°.
16.(3分)(2021春 南召县期末)如图,在△ABC中,∠A=α,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A2020BC和∠A2020CD的平分线交于点A2021,则∠A2021= .
【解题思路】根据题目,需运用特殊到一般的数学思想分析本题.由A1B平分∠ABC,A1C平分∠ACD,,.由三角形外角的性质,得∠A1CD=∠A1BC+∠A1,进而推断出∠A1=∠A1CD﹣∠A1BC.以此类推,可得出结论.
【解答过程】解:∵A1B平分∠ABC,A1C平分∠ACD,
∴,.
∵∠A1CD=∠A1BC+∠A1,
∴∠A1=∠A1CD﹣∠A1BC
.
同理可证,.
∴.
以此类推…
∴.
∵∠A=α,
∴.
故答案为:.
三.解答题(共7小题,满分52分)
17.(6分)(2021 碑林区校级模拟)如图,已知直线l外有一点P,请用尺规作图的方法在直线l上找一点Q,使得Q到P的距离最小(保留作图痕迹,不写作法).
【解题思路】根据垂线段最短,作PQ⊥直线l于Q即可.
【解答过程】解:如图,线段PQ即为所求.
18.(6分)在△ABC中,∠BAC=90°,AD⊥BC于D,CF是∠ACB的平分线,交AD于E,交AB于F,求证:∠AEF=∠AFE.
【解题思路】根据角平分线的定义可得∠ACF=∠BCF,再根据直角三角形两锐角互余可得∠ACF+∠AFE=90°,∠BCF+∠CED=90°,然后得到∠AFE=∠CED,根据对顶角相等可得∠AEF=∠CED,从而得证.
【解答过程】证明:∵CF是∠ACB的平分线,
∴∠ACF=∠BCF,
∵∠BAC=90°,AD⊥BC,
∴∠ACF+∠AFE=90°,∠BCF+∠CED=90°,
∴∠AFE=∠CED,
∵∠AEF=∠CED(对顶角相等),
∴∠AEF=∠AFE.
19.(8分)(2021春 长春期末)如图,点A、B分别在射线OM、ON上运动(不与点O重合),AC、BC分别是∠BAO和∠ABO的角平分线,BC延长线交OM于点G.
解决问题:
(1)若∠OBA=80°,∠OAB=40°,则∠ACG= 60° ;(直接写出答案)
(2)若∠MON=100°,求出∠ACG的度数.
【解题思路】(1)由角平分线的定义可求出∠CBA和∠CAB的度数,再根据三角形外角的性质求出∠ACG的度数即可;
(2)先根据三角形内角和定理求出∠OBA+∠OAB的度数,然后再根据角平分线的定义求出∠CBA+∠CAB的度数,最后根据三角形外角的性质求出结果即可.
【解答过程】解:(1)∵AC、BC分别是∠BAO和∠ABO的角平分线,
∴∠CBA∠ABO,∠CAB∠BAO,
∵∠OBA=80°,∠OAB=40°,
∴∠CBA=40°,∠CAB=20°,
∴∠ACG=∠CBA+∠CAB=60°.
故答案为:60°.
(2)∵∠MON=100°,
∴∠BAO+∠ABO=180°﹣100°=80°,
∵AC、BC分别是∠BAO和∠ABO的角平分线,
∴∠CBA∠ABO,∠CAB∠BAO,
∴∠CBA+∠CAB(∠ABO+∠BAO)80°=40°,
∴∠ACG=∠CBA+∠CAB=40°.
20.(8分)(2020秋 拱墅区期末)如图,AC与BD相交于点O,且OA=OC,OB=OD.
(1)求证:AB∥CD;
(2)直线EF过点O,分别交AB,CD于点E,F,试判断OE与OF是否相等,并说明理由.
【解题思路】(1)∠COD与∠AOB是对顶角,根据SAS可证明△OAB≌△OCD,由全等三角形的性质得到∠A=∠C,即可判定AB∥CD;
(2)在△OAB≌△OCD的基础上证明△EOB≌△FOD.再根据全等三角形的性质得OE=OF.
【解答过程】(1)证明:在△OAB与△OCD中,
,
∴△OAB≌△OCD(SAS),
∴∠A=∠C,
∴AB∥CD;
(2)解:OE=OF,理由如下:
由(1)知,△OAB≌△OCD,
∴∠B=∠D,OB=OD,
在△EOB与△FOD中
,
∴△EOB≌△FOD(ASA),
∴OE=OF.
21.(8分)(2021春 汉台区期末)如图:小刚站在河边的A点处,在河的对面(小刚的正北方向)的B处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树C处,接着再向前走了30步到达D处,然后他左转90°直行,当小刚看到电线塔、树与自己现处的位置E在一条直线时,他共走了140步.
(1)根据题意,画出示意图;
(2)如果小刚一步大约0.5米,估计小刚在点A处时他与电线塔的距离、并说明理由.
【解题思路】(1)根据题意画出图形即可;
(2)根据AAS可得出△ABC≌△DEC,由该全等三角形的性质AB=DE.
【解答过程】解:(1)如图所示;
(2)由题意得,DE=140﹣30﹣30=80(步),
在△ABC和△DEC中,
,
∴△ABC≌△DEC(ASA),
∴AB=DE,
又∵小刚走完DE用来80步,一步大约0.5米,
∴DE=80×0.5=40(米).
答:小刚在点A处时他与电线塔的距离为40米.
22.(8分)(2021春 亭湖区校级期末)如图,△ABC中,CD⊥AB,垂足为D.BE⊥AC,垂足为G,AB=CF,BE=AC.
(1)求证:AE=AF;
(2)AE与AF有何位置关系.请说明理由.
【解题思路】(1)利用SAS证明△AEB≌△FAC可证明结论;
(2)由全等三角形的性质可得∠E=∠CAF,由余角的定义可求得∠EAF的度数即可得解.
【解答过程】(1)证明:∵CD⊥AB,BE⊥AC,
∴∠ADC=∠AGB=90°,
∴∠CAD+∠ACD=∠CAD+∠EBA=90°,
∴∠ACD=∠EBA,
在△AEB和△FAC中,
,
∴△AEB≌△FAC(SAS),
∴AE=AF;
(2)解:AE⊥AF,理由如下:
由(1)知△AEB≌△FAC,
∴∠E=∠CAF,
∵BE⊥AC,垂足为G,
∴∠AGE=90°,
∵∠E+∠EAG=90°,
∴∠CAF+∠EAG=90°,
即∠EAF=90°,
∴AE⊥AF.
23.(8分)(2021春 佛山月考)在△ABC中,AB=AC,点D是射线CB上的一动点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段CB上,且∠BAC=90°时,那么∠DCE= 90 度;
(2)设∠BAC=α,∠DCE=β.
①如图2,当点D在线段CB上,∠BAC≠90°时,请你探究α与β之间的数量关系,并证明你的结论;
②如图3,当点D在线段CB的延长线上,∠BAC≠90°时,请将图3补充完整,写出此时α与β之间的数量关系并证明.
【解题思路】(1)易证∠BAD=∠CAE,即可证明△BAD≌△CAE,可得∠ACE=∠B,即可解题;
(2)易证∠BAD=∠CAE,即可证明△BAD≌△CAE,可得∠ACE=∠B,根据∠B+∠ACB=180°﹣α即可解题;
(3)易证∠BAD=∠CAE,即可证明△BAD≌△CAE,可得∠ACE=∠B,根据∠ADE+∠AED+α=180°,∠CDE+∠CED+β=180°即可解题.
【解答过程】解:(1)∵∠BAD+∠DAC=90°,∠DAC+∠CAE=90°,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴∠ACE=∠B,
∵∠B+∠ACB=90°,
∴∠DCE=∠ACE+∠ACB=90°;
故答案为 90.
(2)∵∠BAD+∠DAC=α,∠DAC+∠CAE=α,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴∠ACE=∠B,
∵∠B+∠ACB=180°﹣α,
∴∠DCE=∠ACE+∠ACB=180°﹣α=β,
∴α+β=180°;
(3)作出图形,
∵∠BAD+∠BAE=α,∠BAE+∠CAE=α,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴∠AEC=∠ADB,
∵∠ADE+∠AED+α=180°,∠CDE+∠CED+β=180°,
∠CED=∠AEC+∠AED,
∴α=β.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
