浙教版初中数学七年级上册第六章《图形的初步认识》单元测试卷(含答案)(困难)
文档属性
| 名称 | 浙教版初中数学七年级上册第六章《图形的初步认识》单元测试卷(含答案)(困难) |  | |
| 格式 | docx | ||
| 文件大小 | 184.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-19 19:04:54 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版初中数学七年级上册第六章《图形的初步认识》单元测试卷(含答案解析)(困难)
考试范围:第六章 考试时间 :120分钟 总分 :120分
第I卷(选择题)
一、选择题(本大题共12小题,共36分。在每小题列出的选项中,选出符合题目的一项)
1. 有一个不完整圆柱形玻璃密封容器如图,测得其底面半径为,高为,其内装蓝色液体若干若如图放置时,测得液面高为;若如图放置时,测得液面高为则该玻璃密封容器的容积圆柱体容积底面积高是( )
A. B. C. D.
2. 对于如图,有两种语言描述:射线;延长线段其中( )
A. 只有正确 B. 只有正确 C. 和均正确 D. 和均错误
3. 如图,王伟同学根据图形写出了四个结论:图中共有条直线;图中共有条射线;图中共有条线段;图中射线与射线是同一条射线;其中结论错误的有( )
A. 个 B. 个 C. 个 D. 个
4. 如图,,,,四点在同一条直线上,是的中点,是的中点,,,那么等于( )
A. B. C. D.
5. 如图,、顺次为线段上的点,且,,为中点,,则的长为( )
A. B. C. D.
6. 把弯曲的公路改直,能够缩短行程,这样做的道理是( )
A. 两点确定一条线段 B. 两点确定一条直线
C. 两点之间线段最短 D. 两点之间直线最短
7. 某海域有相距海里的小岛和,小岛在小岛的北偏东方向,有一艘巡逻艇从小岛出发,沿正东方向航行,同时另一艘巡逻艇以相同的速度从小岛出发,沿直线航行,两只巡逻艇在处相遇,则小岛在相遇地点的方向.( )
A. 南偏西
B. 南偏西
C. 北偏东
D. 南偏东
8. 如图,用同样大小的三角板比较和的大小,下列判断正确的是( )
A. B.
C. D. 没有量角器,无法确定
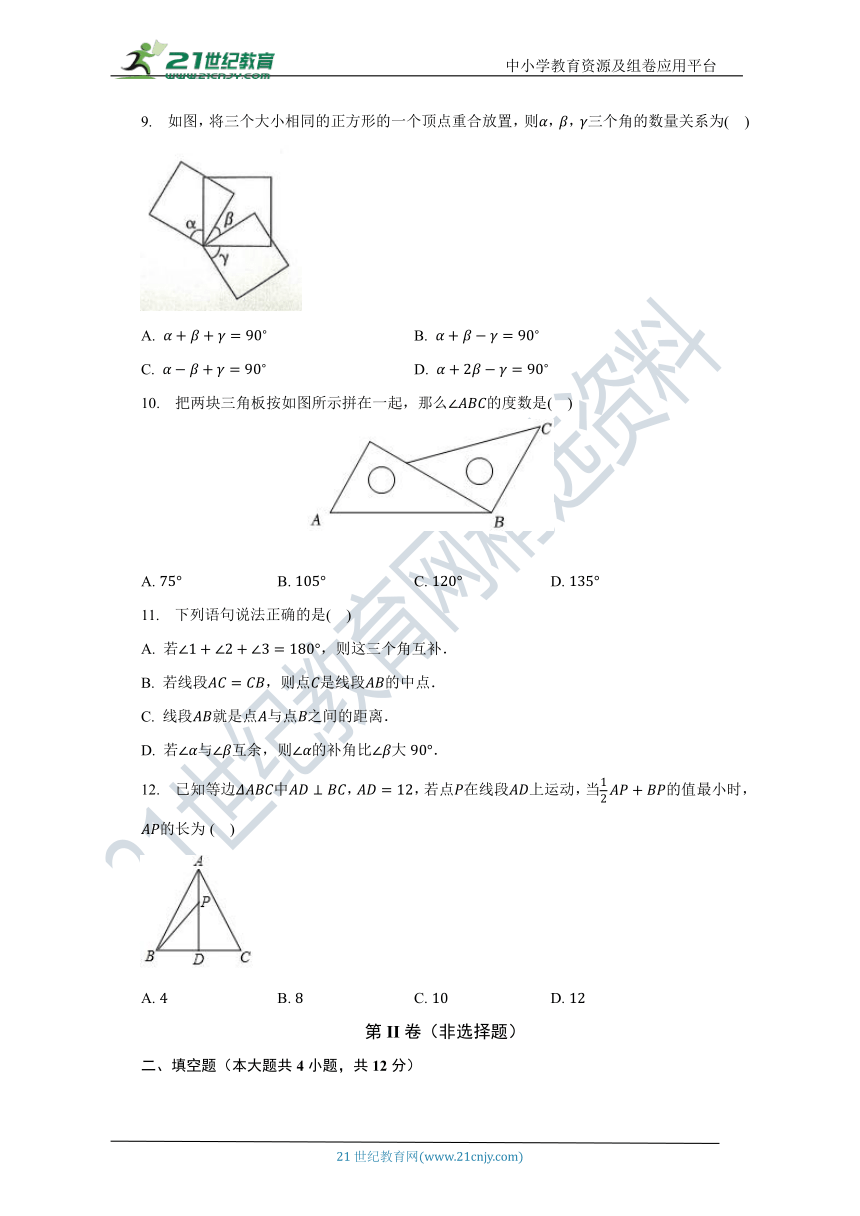
9. 如图,将三个大小相同的正方形的一个顶点重合放置,则,,三个角的数量关系为( )
A. B.
C. D.
10. 把两块三角板按如图所示拼在一起,那么的度数是( )
A. B. C. D.
11. 下列语句说法正确的是( )
A. 若,则这三个角互补.
B. 若线段,则点是线段的中点.
C. 线段就是点与点之间的距离.
D. 若与互余,则的补角比大.
12. 已知等边中,,若点在线段上运动,当的值最小时,的长为( )
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共4小题,共12分)
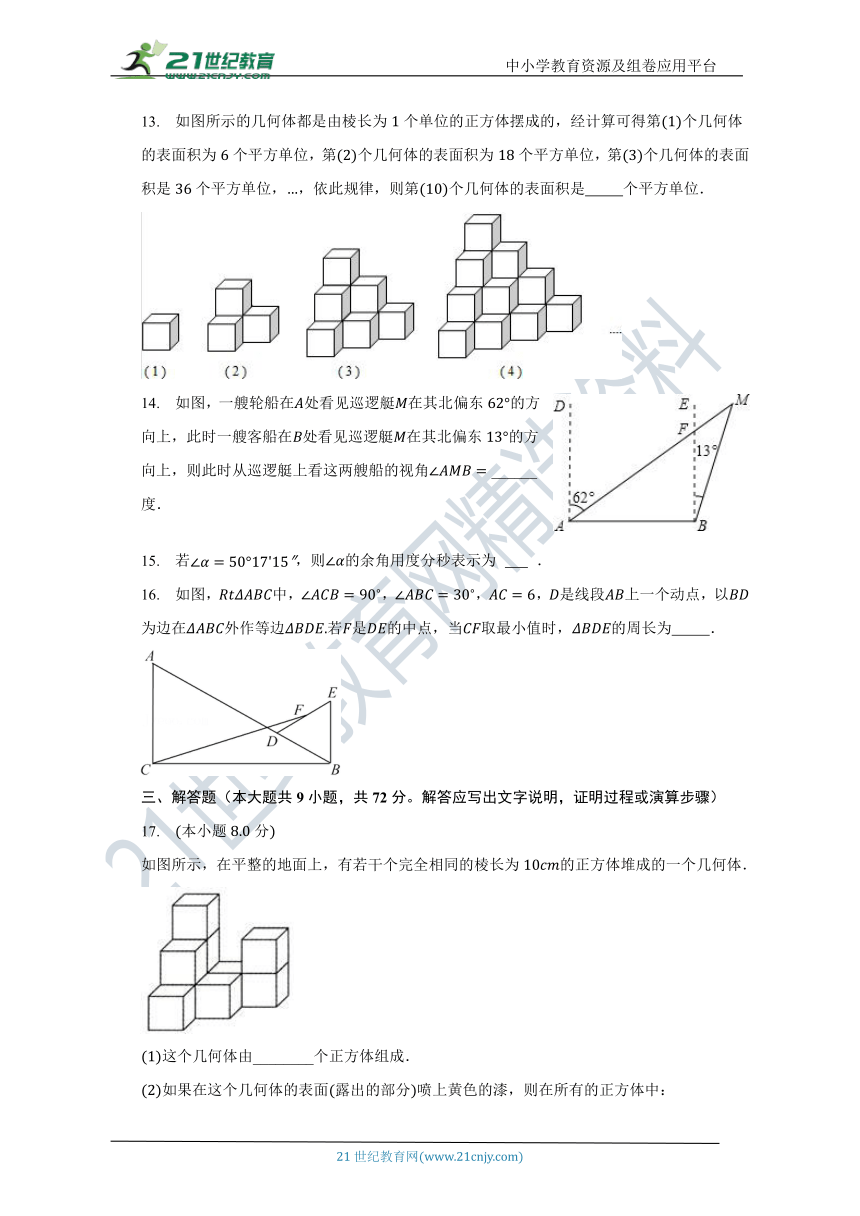
13. 如图所示的几何体都是由棱长为个单位的正方体摆成的,经计算可得第个几何体的表面积为个平方单位,第个几何体的表面积为个平方单位,第个几何体的表面积是个平方单位,,依此规律,则第个几何体的表面积是 个平方单位.
14. 如图,一艘轮船在处看见巡逻艇在其北偏东的方向上,此时一艘客船在处看见巡逻艇在其北偏东的方向上,则此时从巡逻艇上看这两艘船的视角 ______ 度.
15. 若,则的余角用度分秒表示为 .
16. 如图,中,,,,是线段上一个动点,以为边在外作等边若是的中点,当取最小值时,的周长为 .
三、解答题(本大题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
如图所示,在平整的地面上,有若干个完全相同的棱长为的正方体堆成的一个几何体.
这个几何体由________个正方体组成.
如果在这个几何体的表面露出的部分喷上黄色的漆,则在所有的正方体中:
有________个正方体只有一个面是黄色;
有________个正方体只有两个面是黄色;
有________个正方体只有三个面是黄色.
求这个几何体喷漆的面积.
18. 本小题分
如图,平面上有四个点、、、,根据下列语句画图:
画直线、直线交于点;
连接线段、线段交于点;
连接线段,并将其反向延长;
作射线.
19. 本小题分
如图,体育馆与学校处在图形的两个顶点处,出租车从体育馆到学校有两条路线可走,分别用粗线和细线表示.
若粗线总长为,细线总长为,则______填“”“”或“”;
小勇坐出租车由体育馆到学校,如果出租车的收费标准为:行程千米以内起步价元,超过千米的部分每千米元,超过千米的部分每千米元.
到达学校时出租车行驶了千米,小勇身上有元钱,够不够付车费呢?
当出租车行驶路程为千米时,请你计算出租车的收费是多少元?
20. 本小题分
如图,,两点把线段分成三部分,其比为::::,是的中点,,求的长.
21. 本小题分
点为数轴的原点,点、在数轴上的位置如图所示,点表示的数为,线段的长为线段长的倍.点在数轴上,为线段的中点.
点表示的数为______;
若线段的长为,则线段的长为______;
若线段的长为,求线段的长用含的式子表示.
22. 本小题分
轮船以海里时的速度离开港口向东北方向航行,轮船在同时同地以海里时的速度向西北方向航行试求、两船离开港口一个半小时后的距离.
23. 本小题分
将两块直角三角板的顶点叠在一起,已知,,将三角板绕点旋转,在旋转过程中,保持始终在的内部.
如图,若,求的度数.
如图,与有什么数量关系,请说明理由.
如图,若平分,平分,问在旋转过程中,的大小是否发生改变?若不变,请说明理由;若改变,请求出变化范围.
24. 本小题分
如图,为直线上一点,是的平分线,.
的余角是______;
的补角是______;
若,求的度数.
25. 本小题分
如图,,射线在内部,射线在外部,且,.
求的度数:
求证:平分.
答案和解析
1.【答案】
【解析】解:设该玻璃密封容器的容积为,
则,
解得,
故选:.
根据圆柱体的体积公式和图和图中的溶液体积相等,可以列出相应的方程,从而可以得出结论.
本题考查一元一次方程的应用,解答本题的关键是明确题意,列出相应的方程,利用方程的思想解答.
2.【答案】
【解析】解:射线,描述正确;
应该是延长线段,原说法错误.
故选:.
由射线,线段的概念即可判断.
本题考查射线,线段,掌握以上概念是解题的关键.
3.【答案】
【解析】解:图中只有直线,条直线,原说法错误;
以、为端点可以各引出两条射线,以为端点可以引出条射线,以端点可以引出条射线,则图中共有条射线,原说法错误;
图中共有条线段,即线段、、、、、,原说法是正确的;
图中射线与射线不是同一条射线,原说法错误.
故错误的共计个.
故选:.
根据直线、线段、射线的区别逐项分析判断即可.
本题考查了直线、线段、射线的区别与联系,理解三者的区别是解题的关键.
4.【答案】
5.【答案】
【解析】【分析】
本题主要考查了线段的和、差、倍、分.在不同的情况下灵活选用它的不同表示方法,有利于解题的简洁性,同时,灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点.本题关键是得出, 再利用中点的性质得到的长即可.
【解答】
解:,,
,即,
,
,
,
,
为中点,
.
故选A.
6.【答案】
【解析】解:把弯曲的公路改直,能够缩短行程,这样做的道理是:两点之间,线段最短.
故选:.
根据线段的性质即可得出答案.
本题考查了线段的性质.解题的关键是能灵活应用线段的性质.线段的性质:两点之间线段最短.
7.【答案】
【解析】解:小岛在小岛的北偏东方向,
,
,
,
岛在地点的北偏东方向.
故选:.
方向角是从正北或正南方向到目标方向所形成的小于的角,由题意得三角形是等腰三角形,可以求出的角度,从而解决问题.
本题考查方向角,等腰三角形的性质,关键是掌握方向角的定义.
8.【答案】
【解析】解:图中三角尺为等腰直角三角形,
,,
,
故选:.
由图知,,故可比较大小.
本题主要考查角的大小比较,掌握利用中间角比较角的大小是关键.
9.【答案】
【解析】如图,,
.
,
.
10.【答案】
【解析】解:.
故选:.
等于度角与直角的和,据此即可计算得到.
本题考查了角度的计算,理解三角板的角的度数是关键.
11.【答案】
【解析】解:、若两个角的和为,则这两个角互为补角,故A说法错误,不符合题意;
B、若线段,且点在线段上,则点是线段的中点,故B说法错误,不符合题意;
C、线段就是点与点之间的连线段,故C说法错误,不符合题意;
D、因为与互余,
所以,
所以,
即的补角比大,故D说法正确,符合题意.
故选:.
利用余角与补角的定义,中点的定义,线段的定义对各项进行分析即可.
本题主要考查余角与补角,两点间的距离,解答的关键是对相应的知识的掌握.
12.【答案】
【解析】解:如图,
作 于点 ,交 于点 ,
是等边三角形,
,
当 时,
,值最小,
,
此时, .
故选: .
13.【答案】
【解析】【分析】
本题考查了认识立体图形,几何体的表面积和找规律,解决此类问题有两种思路,可以从图形找规律,也可以从数字找规律.本题可以从数字找规律,从而计算出所求的表面积.
【解答】
解:第个几何体的表面积,
第个几何体的表面积,
第个几何体的表面积,
因此得出:第个几何体的表面积,
故答案为:.
14.【答案】
【解析】解:从图中我们可以发现.
将轮船航行的实际问题转化为方向角的问题解答.
解答此类题需要从运动的角度,正确画出方位角,再结合三角形的内角和求解.
15.【答案】
【解析】解:,
故答案为:.
根据“和为的两个角互为余角”,用即可.
本题主要考查余角的定义,度分秒的换算,关键是区分清楚余角和补角的定义.“和为的两个角互为补角”,“和为的两个角互为余角”.
16.【答案】
【解析】解:连接 ,过点 作 交 的延长线于 ,
是等边三角形,点 是 的中点,
,
点 在射线 上运动,
当点 与点 重合时, 最小,
, ,
, ,
,
,
是等边三角形,
,
,
的周长为:,
故答案为:.
17.【答案】解:;
;;;
解:露出表面的面一共有个,
则这个几何体喷漆的面积为,
答:这个几何体喷漆的面积为.
【解析】【分析】
本题考查了认识立体图形,几何体的表面积,小正方体露出面的面积和,露出个面的有两个正方形,露出个面的有两个正方形.
根据几何体的形状,可得左列三排,第一排一层,第二排两层,后排三层,中间列两排,每排一层,右列一排,共一层,可得答案;
根据几何体的形状,可得小正方体露出表面的个数;
根据露出的小正方体的面数,可得几何体的表面积.
【解答】
解:这个几何体由个小正方体组成,
故答案为;
如果在这个几何体的表面喷上黄色的漆,则在所有的小正方体中,有个正方体只有一个面是黄色,有个正方体只有两个面是黄色,有个正方体只有三个面是黄色,
故答案为;;;
见答案.
18.【答案】解:作图如下:
直线、即为所求;
线段、即为所求;
射线即为所求;
射线即为所求.
【解析】连接、并向两方无限延长即可得到直线、;
连接、可得线段、,交点处标点;
连接,并且以为端点向方向延长;
连接,并且以为端点向方向延长.
本题考查作图的知识,难度不大,要熟悉直线、射线、线段的概念,并熟悉基本工具的用法.
19.【答案】解:;
根据题意得到,故小勇身上有元钱,不够付车费
由题意可知当时,;
当时,;
当时,,
综上所述,.
【解析】【分析】
本题考查比较线段的长短以及代数式求值和列代数式的应用,属于中档题.
根据图象可知由图可知两段粗线的距离和与细线的各段的距离和是相等的;
根据题意得到,即可得到答案;
根据条件分段求出即可.
【解答】
解:由图可知两段粗线的距离和与细线的各段的距离和是相等的.
故答案为;
见答案;
见答案.
20.【答案】解:设,则,,
因为是中点,
所以
而.
解得,
所以.
【解析】利用中点性质转化线段之间的倍分关系是解题的关键,在不同的情况下灵活选用它的不同表示方法,有利于解题的简洁性.同时,灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点.设的长为,分别表示出,,进一步利用线段中点的意义和线段的和与差解决问题.
21.【答案】解:;
或;
当,
点在点右侧,
所以
所以
点在线段上,
所以
点在线段上时,
所以,
,
当点在点的左侧时,,
,或,
故:线段的长为:或或
【解析】【分析】
本题考查了列代数式、数轴,解决本题的关键是用数轴表示两点之间的距离.
根据点表示的数为,线段的长为线段长的倍,即可得点表示的数;
根据线段的长为,即可得线段的长;
根据数轴,结合的过程即可用含的式子表示的长.
【解答】
解:因为点表示的数为,线段的长为线段长的倍,
所以
因为,
所以,
所以点表示的数为.
故答案为;
因为,
所以点在原点右侧,
或点在原点左侧,
因为为线段的中点,
所以或,
所以点在原点右侧,
或点在原点左侧,
所以线段的长为或.
故答案为或;
见答案.
22.【答案】解:由题意可得:海里,海里,,
故,
海里,
答:、两船离开港口一个半小时后的距离为海里.
【解析】根据题意得出,根据勾股定理即可得到结论.
此题主要考查了勾股定理的应用,得出是解题关键.
23.【答案】解:因为,,,
所以;
由题意得:,,
所以;
的大小不改变,理由如下:
因为平分,平分,
所以,,
因为,
所以
.
【解析】本题主要考查角的和差和角平分线的定义,解答的关键是结合图形分析清楚各角之间的关系.
结合图形,可得,代入相应数值运算即可;
由图形可得,,从而可求解;
由角平分线定义可得,,结合即可求解.
24.【答案】;
;
因为,,
所以,
因为是的平分线,
所以,
因为,
所以.
【解析】解:因为,
所以,
所以的余角是,
故答案为:;
的补角是,
故答案为:;
见答案.
根据和平角定义可得,再根据余角定义可得答案;
根据如果两个角的和等于平角,就说这两个角互为补角.即其中一个角是另一个角的补角可得答案;
首先计算出的度数,进而可得的度数,再根据角的和差关系可得答案.
此题主要考查了余角和补角,以及角的计算,关键是掌握余角:如果两个角的和等于直角,就说这两个角互为余角.即其中一个角是另一个角的余角.补角:如果两个角的和等于平角,就说这两个角互为补角.即其中一个角是另一个角的补角.
25.【答案】解:,
,
,,
;
证明:,;
又.
,
平分.
【解析】根据垂直的定义得出,根据,,得出;
由的结论得出,进而得出,即可得出平分.
本题考查了垂直的定义,角平分线的定义,数形结合是解题的关键.
21世纪教育网(www.21cnjy.com)
浙教版初中数学七年级上册第六章《图形的初步认识》单元测试卷(含答案解析)(困难)
考试范围:第六章 考试时间 :120分钟 总分 :120分
第I卷(选择题)
一、选择题(本大题共12小题,共36分。在每小题列出的选项中,选出符合题目的一项)
1. 有一个不完整圆柱形玻璃密封容器如图,测得其底面半径为,高为,其内装蓝色液体若干若如图放置时,测得液面高为;若如图放置时,测得液面高为则该玻璃密封容器的容积圆柱体容积底面积高是( )
A. B. C. D.
2. 对于如图,有两种语言描述:射线;延长线段其中( )
A. 只有正确 B. 只有正确 C. 和均正确 D. 和均错误
3. 如图,王伟同学根据图形写出了四个结论:图中共有条直线;图中共有条射线;图中共有条线段;图中射线与射线是同一条射线;其中结论错误的有( )
A. 个 B. 个 C. 个 D. 个
4. 如图,,,,四点在同一条直线上,是的中点,是的中点,,,那么等于( )
A. B. C. D.
5. 如图,、顺次为线段上的点,且,,为中点,,则的长为( )
A. B. C. D.
6. 把弯曲的公路改直,能够缩短行程,这样做的道理是( )
A. 两点确定一条线段 B. 两点确定一条直线
C. 两点之间线段最短 D. 两点之间直线最短
7. 某海域有相距海里的小岛和,小岛在小岛的北偏东方向,有一艘巡逻艇从小岛出发,沿正东方向航行,同时另一艘巡逻艇以相同的速度从小岛出发,沿直线航行,两只巡逻艇在处相遇,则小岛在相遇地点的方向.( )
A. 南偏西
B. 南偏西
C. 北偏东
D. 南偏东
8. 如图,用同样大小的三角板比较和的大小,下列判断正确的是( )
A. B.
C. D. 没有量角器,无法确定
9. 如图,将三个大小相同的正方形的一个顶点重合放置,则,,三个角的数量关系为( )
A. B.
C. D.
10. 把两块三角板按如图所示拼在一起,那么的度数是( )
A. B. C. D.
11. 下列语句说法正确的是( )
A. 若,则这三个角互补.
B. 若线段,则点是线段的中点.
C. 线段就是点与点之间的距离.
D. 若与互余,则的补角比大.
12. 已知等边中,,若点在线段上运动,当的值最小时,的长为( )
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共4小题,共12分)
13. 如图所示的几何体都是由棱长为个单位的正方体摆成的,经计算可得第个几何体的表面积为个平方单位,第个几何体的表面积为个平方单位,第个几何体的表面积是个平方单位,,依此规律,则第个几何体的表面积是 个平方单位.
14. 如图,一艘轮船在处看见巡逻艇在其北偏东的方向上,此时一艘客船在处看见巡逻艇在其北偏东的方向上,则此时从巡逻艇上看这两艘船的视角 ______ 度.
15. 若,则的余角用度分秒表示为 .
16. 如图,中,,,,是线段上一个动点,以为边在外作等边若是的中点,当取最小值时,的周长为 .
三、解答题(本大题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
如图所示,在平整的地面上,有若干个完全相同的棱长为的正方体堆成的一个几何体.
这个几何体由________个正方体组成.
如果在这个几何体的表面露出的部分喷上黄色的漆,则在所有的正方体中:
有________个正方体只有一个面是黄色;
有________个正方体只有两个面是黄色;
有________个正方体只有三个面是黄色.
求这个几何体喷漆的面积.
18. 本小题分
如图,平面上有四个点、、、,根据下列语句画图:
画直线、直线交于点;
连接线段、线段交于点;
连接线段,并将其反向延长;
作射线.
19. 本小题分
如图,体育馆与学校处在图形的两个顶点处,出租车从体育馆到学校有两条路线可走,分别用粗线和细线表示.
若粗线总长为,细线总长为,则______填“”“”或“”;
小勇坐出租车由体育馆到学校,如果出租车的收费标准为:行程千米以内起步价元,超过千米的部分每千米元,超过千米的部分每千米元.
到达学校时出租车行驶了千米,小勇身上有元钱,够不够付车费呢?
当出租车行驶路程为千米时,请你计算出租车的收费是多少元?
20. 本小题分
如图,,两点把线段分成三部分,其比为::::,是的中点,,求的长.
21. 本小题分
点为数轴的原点,点、在数轴上的位置如图所示,点表示的数为,线段的长为线段长的倍.点在数轴上,为线段的中点.
点表示的数为______;
若线段的长为,则线段的长为______;
若线段的长为,求线段的长用含的式子表示.
22. 本小题分
轮船以海里时的速度离开港口向东北方向航行,轮船在同时同地以海里时的速度向西北方向航行试求、两船离开港口一个半小时后的距离.
23. 本小题分
将两块直角三角板的顶点叠在一起,已知,,将三角板绕点旋转,在旋转过程中,保持始终在的内部.
如图,若,求的度数.
如图,与有什么数量关系,请说明理由.
如图,若平分,平分,问在旋转过程中,的大小是否发生改变?若不变,请说明理由;若改变,请求出变化范围.
24. 本小题分
如图,为直线上一点,是的平分线,.
的余角是______;
的补角是______;
若,求的度数.
25. 本小题分
如图,,射线在内部,射线在外部,且,.
求的度数:
求证:平分.
答案和解析
1.【答案】
【解析】解:设该玻璃密封容器的容积为,
则,
解得,
故选:.
根据圆柱体的体积公式和图和图中的溶液体积相等,可以列出相应的方程,从而可以得出结论.
本题考查一元一次方程的应用,解答本题的关键是明确题意,列出相应的方程,利用方程的思想解答.
2.【答案】
【解析】解:射线,描述正确;
应该是延长线段,原说法错误.
故选:.
由射线,线段的概念即可判断.
本题考查射线,线段,掌握以上概念是解题的关键.
3.【答案】
【解析】解:图中只有直线,条直线,原说法错误;
以、为端点可以各引出两条射线,以为端点可以引出条射线,以端点可以引出条射线,则图中共有条射线,原说法错误;
图中共有条线段,即线段、、、、、,原说法是正确的;
图中射线与射线不是同一条射线,原说法错误.
故错误的共计个.
故选:.
根据直线、线段、射线的区别逐项分析判断即可.
本题考查了直线、线段、射线的区别与联系,理解三者的区别是解题的关键.
4.【答案】
5.【答案】
【解析】【分析】
本题主要考查了线段的和、差、倍、分.在不同的情况下灵活选用它的不同表示方法,有利于解题的简洁性,同时,灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点.本题关键是得出, 再利用中点的性质得到的长即可.
【解答】
解:,,
,即,
,
,
,
,
为中点,
.
故选A.
6.【答案】
【解析】解:把弯曲的公路改直,能够缩短行程,这样做的道理是:两点之间,线段最短.
故选:.
根据线段的性质即可得出答案.
本题考查了线段的性质.解题的关键是能灵活应用线段的性质.线段的性质:两点之间线段最短.
7.【答案】
【解析】解:小岛在小岛的北偏东方向,
,
,
,
岛在地点的北偏东方向.
故选:.
方向角是从正北或正南方向到目标方向所形成的小于的角,由题意得三角形是等腰三角形,可以求出的角度,从而解决问题.
本题考查方向角,等腰三角形的性质,关键是掌握方向角的定义.
8.【答案】
【解析】解:图中三角尺为等腰直角三角形,
,,
,
故选:.
由图知,,故可比较大小.
本题主要考查角的大小比较,掌握利用中间角比较角的大小是关键.
9.【答案】
【解析】如图,,
.
,
.
10.【答案】
【解析】解:.
故选:.
等于度角与直角的和,据此即可计算得到.
本题考查了角度的计算,理解三角板的角的度数是关键.
11.【答案】
【解析】解:、若两个角的和为,则这两个角互为补角,故A说法错误,不符合题意;
B、若线段,且点在线段上,则点是线段的中点,故B说法错误,不符合题意;
C、线段就是点与点之间的连线段,故C说法错误,不符合题意;
D、因为与互余,
所以,
所以,
即的补角比大,故D说法正确,符合题意.
故选:.
利用余角与补角的定义,中点的定义,线段的定义对各项进行分析即可.
本题主要考查余角与补角,两点间的距离,解答的关键是对相应的知识的掌握.
12.【答案】
【解析】解:如图,
作 于点 ,交 于点 ,
是等边三角形,
,
当 时,
,值最小,
,
此时, .
故选: .
13.【答案】
【解析】【分析】
本题考查了认识立体图形,几何体的表面积和找规律,解决此类问题有两种思路,可以从图形找规律,也可以从数字找规律.本题可以从数字找规律,从而计算出所求的表面积.
【解答】
解:第个几何体的表面积,
第个几何体的表面积,
第个几何体的表面积,
因此得出:第个几何体的表面积,
故答案为:.
14.【答案】
【解析】解:从图中我们可以发现.
将轮船航行的实际问题转化为方向角的问题解答.
解答此类题需要从运动的角度,正确画出方位角,再结合三角形的内角和求解.
15.【答案】
【解析】解:,
故答案为:.
根据“和为的两个角互为余角”,用即可.
本题主要考查余角的定义,度分秒的换算,关键是区分清楚余角和补角的定义.“和为的两个角互为补角”,“和为的两个角互为余角”.
16.【答案】
【解析】解:连接 ,过点 作 交 的延长线于 ,
是等边三角形,点 是 的中点,
,
点 在射线 上运动,
当点 与点 重合时, 最小,
, ,
, ,
,
,
是等边三角形,
,
,
的周长为:,
故答案为:.
17.【答案】解:;
;;;
解:露出表面的面一共有个,
则这个几何体喷漆的面积为,
答:这个几何体喷漆的面积为.
【解析】【分析】
本题考查了认识立体图形,几何体的表面积,小正方体露出面的面积和,露出个面的有两个正方形,露出个面的有两个正方形.
根据几何体的形状,可得左列三排,第一排一层,第二排两层,后排三层,中间列两排,每排一层,右列一排,共一层,可得答案;
根据几何体的形状,可得小正方体露出表面的个数;
根据露出的小正方体的面数,可得几何体的表面积.
【解答】
解:这个几何体由个小正方体组成,
故答案为;
如果在这个几何体的表面喷上黄色的漆,则在所有的小正方体中,有个正方体只有一个面是黄色,有个正方体只有两个面是黄色,有个正方体只有三个面是黄色,
故答案为;;;
见答案.
18.【答案】解:作图如下:
直线、即为所求;
线段、即为所求;
射线即为所求;
射线即为所求.
【解析】连接、并向两方无限延长即可得到直线、;
连接、可得线段、,交点处标点;
连接,并且以为端点向方向延长;
连接,并且以为端点向方向延长.
本题考查作图的知识,难度不大,要熟悉直线、射线、线段的概念,并熟悉基本工具的用法.
19.【答案】解:;
根据题意得到,故小勇身上有元钱,不够付车费
由题意可知当时,;
当时,;
当时,,
综上所述,.
【解析】【分析】
本题考查比较线段的长短以及代数式求值和列代数式的应用,属于中档题.
根据图象可知由图可知两段粗线的距离和与细线的各段的距离和是相等的;
根据题意得到,即可得到答案;
根据条件分段求出即可.
【解答】
解:由图可知两段粗线的距离和与细线的各段的距离和是相等的.
故答案为;
见答案;
见答案.
20.【答案】解:设,则,,
因为是中点,
所以
而.
解得,
所以.
【解析】利用中点性质转化线段之间的倍分关系是解题的关键,在不同的情况下灵活选用它的不同表示方法,有利于解题的简洁性.同时,灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点.设的长为,分别表示出,,进一步利用线段中点的意义和线段的和与差解决问题.
21.【答案】解:;
或;
当,
点在点右侧,
所以
所以
点在线段上,
所以
点在线段上时,
所以,
,
当点在点的左侧时,,
,或,
故:线段的长为:或或
【解析】【分析】
本题考查了列代数式、数轴,解决本题的关键是用数轴表示两点之间的距离.
根据点表示的数为,线段的长为线段长的倍,即可得点表示的数;
根据线段的长为,即可得线段的长;
根据数轴,结合的过程即可用含的式子表示的长.
【解答】
解:因为点表示的数为,线段的长为线段长的倍,
所以
因为,
所以,
所以点表示的数为.
故答案为;
因为,
所以点在原点右侧,
或点在原点左侧,
因为为线段的中点,
所以或,
所以点在原点右侧,
或点在原点左侧,
所以线段的长为或.
故答案为或;
见答案.
22.【答案】解:由题意可得:海里,海里,,
故,
海里,
答:、两船离开港口一个半小时后的距离为海里.
【解析】根据题意得出,根据勾股定理即可得到结论.
此题主要考查了勾股定理的应用,得出是解题关键.
23.【答案】解:因为,,,
所以;
由题意得:,,
所以;
的大小不改变,理由如下:
因为平分,平分,
所以,,
因为,
所以
.
【解析】本题主要考查角的和差和角平分线的定义,解答的关键是结合图形分析清楚各角之间的关系.
结合图形,可得,代入相应数值运算即可;
由图形可得,,从而可求解;
由角平分线定义可得,,结合即可求解.
24.【答案】;
;
因为,,
所以,
因为是的平分线,
所以,
因为,
所以.
【解析】解:因为,
所以,
所以的余角是,
故答案为:;
的补角是,
故答案为:;
见答案.
根据和平角定义可得,再根据余角定义可得答案;
根据如果两个角的和等于平角,就说这两个角互为补角.即其中一个角是另一个角的补角可得答案;
首先计算出的度数,进而可得的度数,再根据角的和差关系可得答案.
此题主要考查了余角和补角,以及角的计算,关键是掌握余角:如果两个角的和等于直角,就说这两个角互为余角.即其中一个角是另一个角的余角.补角:如果两个角的和等于平角,就说这两个角互为补角.即其中一个角是另一个角的补角.
25.【答案】解:,
,
,,
;
证明:,;
又.
,
平分.
【解析】根据垂直的定义得出,根据,,得出;
由的结论得出,进而得出,即可得出平分.
本题考查了垂直的定义,角平分线的定义,数形结合是解题的关键.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
