期末复习一从自然数到有理数复习

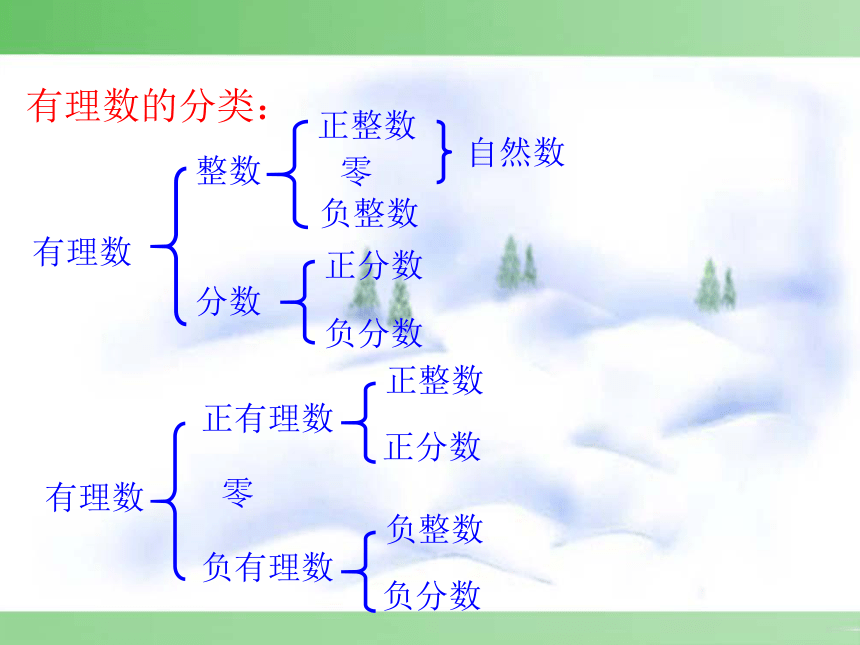
课件24张PPT。第一章 有理数的复习制作：张喜林有理数有理数的分类：有理数正整数集合{ …}
负分数集合{ …}正数集合{ …}
非负有理数集合{ …}1, +10, 1， 8.9，+10，1，8.9，+10，0,1、把以下数填在相应的大括号里。
1， ，8.9，-7， ，+10，0； ,数轴：规定了原点、正方向、单位长度的直线叫做数轴。
任何一个有理数都可以用数轴上的一个点来表示。
如上图：
　　A点表示＿＿；
　　B点表示＿＿；
　　C点表示＿＿；
　　D点表示＿＿：
　　E点表示＿＿。1、在数轴上，原点及原点左边所表示的数是（　）
Ａ整数　 Ｂ负数　
Ｃ非负数　 Ｄ非正数
2、下列语句中正确的是（　）　　　　　　　　　
Ａ数轴上的点只能表示整数　
Ｂ数轴上的点只能表示分数　
Ｃ数轴上的点只能表示有理数
Ｄ所有有理数都可以用数轴上的点表示出来DD相反数：只有符号不同的两个数互为相反数 0的相反数是0。互为相反数的两个数相加，和为0。例如：5＋（－5）＝0一个数 相反数是 。例如： 　3的相反数是－3
－4的相反数是－（－4）＝4乘积是1的两个数互为倒数。0没有倒数。倒数： 的倒数是 3、用-a表示的数一定是（ ）
A、 负数，B 、正数，C、 正数或负数，D、都不对
4、一个数的相反数是最小的正整数，那么这个数是（ ） A 、–1， B、 1， C 、±1， D、 0
5、判断题
①互为相反数的两个数在数轴上位于原点两旁（ ）
②在一个数前面添上“-”号，它就成了一个负数（ ）
③ 只要符号不同，这两个数就是相反数（ ）DA×××从数轴上看，一个数的绝对值就是表示这个数的点离开原点的距离。　　　例如：正数的绝对值是 ；
0的绝对值是 ；
负数的绝对值是 。绝对值：数　的绝对值记为即:它的本身它的相反数01、绝对值的意义是
（1）__________________________________；
（2）__________________________________；
（3）__________________________________；
（4）|a|___________0.一个正数的绝对值是它本身一个负数数的绝对值是它的相反数0的绝对值是0大于或者等于2 、化简
（1） （2）|-3.3|-|+4.3|＝___；
（3） （4） -13、填空题。
（1）、若|a|＝3，则a＝____； |a+1|＝0，则a＝___。
（2）、若|a-5|+|b+3|＝0，则a＝___，b＝___。
（3）、若|x+2|+|y-2|＝0，则x＝___，y＝___。±3-15-3-22例1：用“＞”、“＝”、“＜”填空
1、若a＜0，b＜0，|a|＜|b|，则a＋b____0
2、若a＞0，b＜0，|a|＞|b|，则a＋b____0
3、若a＜0，b＞0，|a|＞|b|，则a＋b____0
4、若a＜0，b＞0，|a|＝|b|，则a＋b____0
5、若a＜0，b＜0，|a|＜|b|，则a－b____0
6、若a＜0，b＞0，|a|＜|b|，则－a－b____0＜＞＜＝＞＜大于3.142的负整数有　　　　个；
小于2.9的正数有 个；
大于－9.5的负整数有 个.绝对值小于2的整数有________。
绝对值等于它本身的数有___________。
绝对值不大于3的负整数有__________。-1，0，1非负数-1，-2，-30无数91、下列说法错误的是（ ）（A）自然数一定是有理数（B）自然数一定是整数（C）自然数一定是非负数（D）整数一定是自然数3、对于任何有理数a，下列一定为负数的是 （ ）（A） -(-3+a) （B） -a （C）-|a+1|（D） -|a|-12、绝对值大于 而小于 的自然数有__________DD1，2a+b=0c d=1　　
　　正数都大于0，负数都小于0。即负数＜0＜正数。
　　数轴上两个点表示的数，右边的总比左边的大。
　　两个负数，绝对值大的反而小。有理数的大小比较：2、数轴上点A、B分别表示-4和3，则线段AB的长度为________3、已知数轴上点A、B分别表示-2和x，若AB=3，则x的值为________D-5或174、填空题
①比－3大的负整数是_______________；　

②已知ｍ是整数且-2
③有理数中，最大的负整数是______，最小的正整数是______。最大的非正数是__________。　

④与原点的距离为三个单位的点有_______个，他们分别表示的有理数是_____和_______。-2，-1-1，0，1，2-1102-22有理数的加法 有理数的加法法则：
1. 同号两数相加，取相同的符号，并把绝对值相加；
2. 绝对值不等的异号两数相加，取绝对值较大加数的符号，并用较大的绝对值减去较小的绝对值；
3. 互为相反数的两个数相加得0；
4. 一个数同0相加，仍得这个数.有理数的减法有理数减法法则:减去一个数，等于加上这个数的相反数.减号变加号

(1)(-32) -(+5)=(-32)+(-5)=-37.

减数变相反数
例：小明和小强在游戏中规定，长方形表示加，圆形表示减，结果小者为胜。请你当裁判，判定谁是胜者。
小明： 4.5 3.2 1.1 1.4

小强： －8 2 －6 －7解：小明：－4.5＋3.2－1.1＋1.4
＝－4.5 －1.1 ＋3.2 ＋1.4
＝－5.6＋4.6＝－1小强： ＋(－8)－2＋(－6)－(－7)
＝－8－2－6＋7
＝－16＋7＝－9因为－1 ＞－9，结果判定小强胜。2. 蚂蚁从某点O出发在一条直线上来回爬行，假定向右爬行的路程为正数，向左爬行的路程为负数，爬过的各段路程依次为（单位：厘米）
+6，-3，+10，-5，-7，+13，-10
（1）蚂蚁最后是否回到了出发点？
（2）蚂蚁离开出发点O最远是多少厘米？
（3）在爬行过程中，如果爬行1厘米奖励一粒芝麻，则蚂蚁一共得到多少粒芝麻？+413厘米54粒 4、选择题：
（1）较小的数减去较大的数，所得的数一定是（ ）
A 0 B 正数 C 负数 D 0或负数 （2）下列说法正确的是（ ）
A 减去一个 负数，差一定大于被减数；
B 减去一个正数，差不一定小于被减数；
C 0 减去任何数，差都是负数；
D 两个数之差一定小于被减数；
CA（3）下列说法正确的是（ ）
A 减去一个数，等于加上这个数；
B 有理数的减法中，被减数不一定比减数大；
C 0 减去一个数 ，仍得 这个数；
D 两个相反数相减得 0 ；
（4）差是-5，被减数是-2，则减数为（ ）
A -7 B -3 C 3 D -7
BC再见