期末复习二-从自然数到有理数复习
图片预览









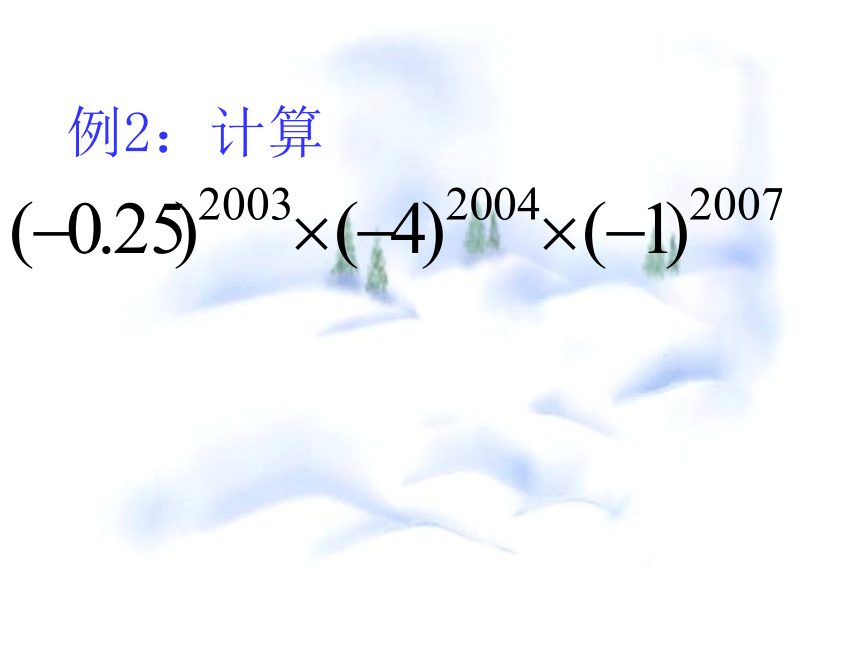

文档简介
课件36张PPT。有理数的运算复习 有理数的五种运算1.运算法则
2.运算顺序
3.运 算 律1.运算法则1)有理数加法法则
2)有理数减法法则
3)有理数乘法法则
4)有理数除法法则
5)有理数的乘方1)有理数加法法则① 同号两数相加,取相同的符号,并把绝对值相加;② 异号两数相加,取绝对值较大
的加数的符号,并用较大的绝对值
减去较小的绝对值;互为相反数
的两数相加得0; ③ 一个数同0相加,仍得这个数。2)有理数减法法则 减去一个数,
等于加上这个数的相反数.
即 a-b=a+(-b)例:分别求出数轴上两点间的距离:
①表示2的点与表示-7的点;
②表示-3的点与表示-1的点。解:①︱2-(-7)︱=︱2+7︱=︱9︱=9
②︱-3-(-1)︱=︱-3+1︱=︱-2︱=23)有理数的乘法法则 两数相乘,同号得正,异号得负,并把绝对值相乘;
任何数同0相乘,都得0.① 几个不等于0的数相乘,积的符号
由负因数的个数决定,当负因数有奇
数个时,积为负;当负因数有偶数个
时,积为正.② 几个数相乘,有一个因数为0,
积就为0.4)有理数除法法则①除以一个数等于乘上这个数的倒数;
即② 两数相除,同号得正,异号得负,
并把绝对值相除;
0除以任何一个不等于0的数,都
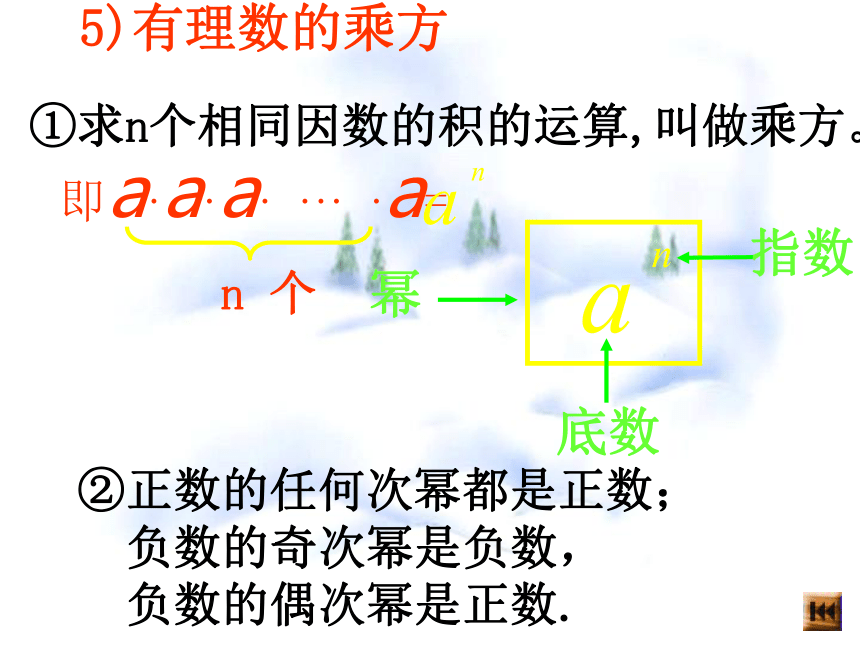
得0.5)有理数的乘方 ①求n个相同因数的积的运算,叫做乘方。②正数的任何次幂都是正数;
负数的奇次幂是负数,
负数的偶次幂是正数.2.运算顺序1)有括号,先算括号里面的;
2)先算乘方,再算乘除,
最后算加减;
3)对只含乘除,或只含加减的
运算,应从左往右运算。例题讲析例1:观察下列解题过程,计算:
解:设s= (1) 则由(2)-(1)得2s=所以s=通过阅读,请你用学到的方法计算:例2:计算例3:看一看猜一猜:请阅读下列材料《西游记》中有这么一段:话说悟空惹恼了师傅唐僧,唐僧便念起金箍咒来,痛得悟空抱头叫嚷:“疼死我也”。假如悟空头上的金箍咒缩短了1cm,那么金箍咒要陷进头皮多么毫米?(π取3.14,结果保留两位小数)例4:详解:设戴在悟空头上的金箍咒的半径为R,收缩后的小圆的半径为r,由题意得:
2π (R – r)= 1
R – r =≈ 0.16(mm)答:略例5:古时候某个王国里有一位聪明的大臣,他发明了国际象棋献给了国王,国王从此迷上了下棋,为了对聪明的大臣表示感谢,国王答应满足这位大臣的一个要求。大臣说:“就在这个棋盘上放些米粒吧,第1格放1粒,第2格放2粒,第3格放4粒,第4格放8粒,然后依次为16粒,32粒……直到第64格。”“你真傻,就要这么一点米粒?!”国王哈哈大笑,大臣说:“就怕您国库里没有这么多米。”你认为国王的国库里有这么多米吗? 若10000粒米为1斤,100斤为1麻袋,那么这位大臣要的大米约合多少麻袋呢?友情提醒仔细想想,你准行的哟
解:根据题意,得:
重点点击:一、关于数轴
例1、若有理数m>n,在数轴上点M表示数m,点N表示数n,那么( )
A、点M在点N的左边
B、点M在点N的右边
C、点M在原点的右边,点N在原点的左边
D、点M和N都在原点的右边B点拔:在数轴上,大数总在小数的右边二、关于相反数例2、试比较a与-a的大小。
解:
例3、已知3m+7与m-3互为相反数,求m的值。
解:
归纳:不能直观地把a当作正数,-a当作负数。归纳:a与b互为相反数,则a+b=0。当a>0时,a> -a;当a<0时, a<-a;
当a=0时,a=-a。
3m+7+m-3=0,解之,m=-1关于绝对值例1、绝对值小于7的所有整数之积为( )0例2、已知|a|<|b|,且a>0,b<0,把a、b、-a、-b按次序由大到小排列。解:-b>a>-a> b小结:此类题目可用特殊值法,但要注意,所选的特殊值不能出现在解题过程中。例3、有理数a、b、c在数轴上的对应点如图,化简|a-b|+|a+b|+|c-a|-|c-b|。 注意:这类题目既考了绝对值的知识,又考了去括号的知识,还结合了数轴,有一定的难度,要格外小心。(1)判断题
1、运用加法交换律,得-7+3=-3+7.( )
2、4-5-1=-5+4-1 ( )
3、(-2)-(-3)+(+7)=7-2-3. ( )
4、(+7)-(-3)+(-8)=7+3-8. ( )
5、-7-5+(-3)=-9. ( )
6、-7-5+(-3)=-5. ( )
7、若 a + b = 0,则 |a|=|b| ( )
8、若|a|=|b|,则 a = b ( )
9、若|a|=|b|,则a + b = 0 ( )动一动,试一试!1、下列说法正确的是 ( )
A 、在0和+1之间没有正数
B 、在0和+1之间的有理数有无穷多个
C、在-1和+1之间没有负数
D、在-1和+1之间的有理数只有0
2、下列说法正确的是( )
A 、数轴上右边的表示的数是正数
B 、数轴是一条直线
C、 距离数轴越远的点,表示的数越大
D、 任何一个有理数,都可以用数轴上的点表示出来(2)选择题3、-2-1+3的值等于 ( )
A.0 B.2 C.-2 D.-3
4、下列计算正确的是 ( )
A.-3-5=2 B.2-8=-6
C.(-6)-(-3)-(-1)=-10 D.0-10=10
5、两个数相加,其和小于每个加数,那么这两个数( )
A.同为负数 B.异号 C.同为正数 D.零或负数8、a、b为两个有理数,如果a+b>0,那么一定有( )
A.a、b中,一个为正数,另一个为0
B.a>0,b>0
C.a、b中,一个为正,另一个为负,
且正数的绝对值大于负数的绝对值
D.a、b中至少有一个为正数
9、甲数减去乙数的差与甲数比较,必为( )
A.差一定小于甲数 B.差不能大于甲数
C.差一定大于甲数 D.差的大小取决于乙是什么样的数
10、如果|a|+|b|≠0,那么下面说法中正确的是( )
A.a、b均不为零 B.a、b至少有一个为零
C.a、b不都为零 D.a、b都为零
1、设a 为正数,b为负数,则下列各式的符号是正还是负?
(1)a-b (2)1-b (3)-a+b (4)0-a
2、已知数轴上有A,B两点,A,B之间的距离是1,点A与原点O的距离为3,那么 所有满足条件的点B与原点的距离之和等于多少?
3、若数a+b=0,b+c=0,c+d=0,d+f=0, 则:a,b,c,d,f五个数中哪些数是互为相反数,哪些数是相等?4、 (1-a)的相反数是什么? (1+a)与什么是互为相反数? -(-3)的相反数是什么? 解答题(5)若|x-2|+|y+3|+|z-5|=0。
计算:(1)x,y,z的值.
(2)求|x|+|y|+|z|的值. (3)当a=12,b=-4时,求|a+b|-|b|的值练习与巩固:1、绝对值最小的数是___,绝对值等于本身的数是__,平方等于它本身的数有__,立方等于它本身的数有___。
2、下列说法中,正确的有( )
⑴绝对值相等的两个数必相同或互为相反数
⑵正数和零的绝对值等于它本身
⑶只有负数的绝对值是它的相反数
⑷一个数的绝对值必为正。
A、1个 B、2个 C、3个 D、4个
3、若|x-5|+ |y+3|=0,求2x+3y的值。拓展延伸:1、趣味题:小明参加“趣味数学”选修课,课上老师给了一个问题,小明看了很为难,你能帮他一下吗?a、b互为相反数,c、d互为负倒数,
|m|=2,则 -1+m-cd的值为多少?
2、满足|a-b|= |a|+|b|成立的条件是( )
A、ab>0 B、 ab>1 C、ab≤0 D、ab≤ 1 本章难点1、有关零:(1)零既不是正数也不是负数,零大于负数,正数大于零。(2)零的相反数是它本身,零的绝对值是它本身,零的任何非零次幂是零。(3)零是绝对值最小的有理数。(4)零乘以任何数为零,零除以任何不为零的数为零。(5)零没有倒数,零不能做除数。2、有理数中的最值(1) 最小的自然数
(2) 最大的负整数
(3) 绝对值最小的有理数
(4) 平方最小的有理数1 – 100有理数的形式含绝对值的式子的化简|a|=3,|b|=4,求a-b的值分类讨论思想有关乘方的习题
2.运算顺序
3.运 算 律1.运算法则1)有理数加法法则
2)有理数减法法则
3)有理数乘法法则
4)有理数除法法则
5)有理数的乘方1)有理数加法法则① 同号两数相加,取相同的符号,并把绝对值相加;② 异号两数相加,取绝对值较大
的加数的符号,并用较大的绝对值
减去较小的绝对值;互为相反数
的两数相加得0; ③ 一个数同0相加,仍得这个数。2)有理数减法法则 减去一个数,
等于加上这个数的相反数.
即 a-b=a+(-b)例:分别求出数轴上两点间的距离:
①表示2的点与表示-7的点;
②表示-3的点与表示-1的点。解:①︱2-(-7)︱=︱2+7︱=︱9︱=9
②︱-3-(-1)︱=︱-3+1︱=︱-2︱=23)有理数的乘法法则 两数相乘,同号得正,异号得负,并把绝对值相乘;
任何数同0相乘,都得0.① 几个不等于0的数相乘,积的符号
由负因数的个数决定,当负因数有奇
数个时,积为负;当负因数有偶数个
时,积为正.② 几个数相乘,有一个因数为0,
积就为0.4)有理数除法法则①除以一个数等于乘上这个数的倒数;
即② 两数相除,同号得正,异号得负,
并把绝对值相除;
0除以任何一个不等于0的数,都
得0.5)有理数的乘方 ①求n个相同因数的积的运算,叫做乘方。②正数的任何次幂都是正数;
负数的奇次幂是负数,
负数的偶次幂是正数.2.运算顺序1)有括号,先算括号里面的;
2)先算乘方,再算乘除,
最后算加减;
3)对只含乘除,或只含加减的
运算,应从左往右运算。例题讲析例1:观察下列解题过程,计算:
解:设s= (1) 则由(2)-(1)得2s=所以s=通过阅读,请你用学到的方法计算:例2:计算例3:看一看猜一猜:请阅读下列材料《西游记》中有这么一段:话说悟空惹恼了师傅唐僧,唐僧便念起金箍咒来,痛得悟空抱头叫嚷:“疼死我也”。假如悟空头上的金箍咒缩短了1cm,那么金箍咒要陷进头皮多么毫米?(π取3.14,结果保留两位小数)例4:详解:设戴在悟空头上的金箍咒的半径为R,收缩后的小圆的半径为r,由题意得:
2π (R – r)= 1
R – r =≈ 0.16(mm)答:略例5:古时候某个王国里有一位聪明的大臣,他发明了国际象棋献给了国王,国王从此迷上了下棋,为了对聪明的大臣表示感谢,国王答应满足这位大臣的一个要求。大臣说:“就在这个棋盘上放些米粒吧,第1格放1粒,第2格放2粒,第3格放4粒,第4格放8粒,然后依次为16粒,32粒……直到第64格。”“你真傻,就要这么一点米粒?!”国王哈哈大笑,大臣说:“就怕您国库里没有这么多米。”你认为国王的国库里有这么多米吗? 若10000粒米为1斤,100斤为1麻袋,那么这位大臣要的大米约合多少麻袋呢?友情提醒仔细想想,你准行的哟
解:根据题意,得:
重点点击:一、关于数轴
例1、若有理数m>n,在数轴上点M表示数m,点N表示数n,那么( )
A、点M在点N的左边
B、点M在点N的右边
C、点M在原点的右边,点N在原点的左边
D、点M和N都在原点的右边B点拔:在数轴上,大数总在小数的右边二、关于相反数例2、试比较a与-a的大小。
解:
例3、已知3m+7与m-3互为相反数,求m的值。
解:
归纳:不能直观地把a当作正数,-a当作负数。归纳:a与b互为相反数,则a+b=0。当a>0时,a> -a;当a<0时, a<-a;
当a=0时,a=-a。
3m+7+m-3=0,解之,m=-1关于绝对值例1、绝对值小于7的所有整数之积为( )0例2、已知|a|<|b|,且a>0,b<0,把a、b、-a、-b按次序由大到小排列。解:-b>a>-a> b小结:此类题目可用特殊值法,但要注意,所选的特殊值不能出现在解题过程中。例3、有理数a、b、c在数轴上的对应点如图,化简|a-b|+|a+b|+|c-a|-|c-b|。 注意:这类题目既考了绝对值的知识,又考了去括号的知识,还结合了数轴,有一定的难度,要格外小心。(1)判断题
1、运用加法交换律,得-7+3=-3+7.( )
2、4-5-1=-5+4-1 ( )
3、(-2)-(-3)+(+7)=7-2-3. ( )
4、(+7)-(-3)+(-8)=7+3-8. ( )
5、-7-5+(-3)=-9. ( )
6、-7-5+(-3)=-5. ( )
7、若 a + b = 0,则 |a|=|b| ( )
8、若|a|=|b|,则 a = b ( )
9、若|a|=|b|,则a + b = 0 ( )动一动,试一试!1、下列说法正确的是 ( )
A 、在0和+1之间没有正数
B 、在0和+1之间的有理数有无穷多个
C、在-1和+1之间没有负数
D、在-1和+1之间的有理数只有0
2、下列说法正确的是( )
A 、数轴上右边的表示的数是正数
B 、数轴是一条直线
C、 距离数轴越远的点,表示的数越大
D、 任何一个有理数,都可以用数轴上的点表示出来(2)选择题3、-2-1+3的值等于 ( )
A.0 B.2 C.-2 D.-3
4、下列计算正确的是 ( )
A.-3-5=2 B.2-8=-6
C.(-6)-(-3)-(-1)=-10 D.0-10=10
5、两个数相加,其和小于每个加数,那么这两个数( )
A.同为负数 B.异号 C.同为正数 D.零或负数8、a、b为两个有理数,如果a+b>0,那么一定有( )
A.a、b中,一个为正数,另一个为0
B.a>0,b>0
C.a、b中,一个为正,另一个为负,
且正数的绝对值大于负数的绝对值
D.a、b中至少有一个为正数
9、甲数减去乙数的差与甲数比较,必为( )
A.差一定小于甲数 B.差不能大于甲数
C.差一定大于甲数 D.差的大小取决于乙是什么样的数
10、如果|a|+|b|≠0,那么下面说法中正确的是( )
A.a、b均不为零 B.a、b至少有一个为零
C.a、b不都为零 D.a、b都为零
1、设a 为正数,b为负数,则下列各式的符号是正还是负?
(1)a-b (2)1-b (3)-a+b (4)0-a
2、已知数轴上有A,B两点,A,B之间的距离是1,点A与原点O的距离为3,那么 所有满足条件的点B与原点的距离之和等于多少?
3、若数a+b=0,b+c=0,c+d=0,d+f=0, 则:a,b,c,d,f五个数中哪些数是互为相反数,哪些数是相等?4、 (1-a)的相反数是什么? (1+a)与什么是互为相反数? -(-3)的相反数是什么? 解答题(5)若|x-2|+|y+3|+|z-5|=0。
计算:(1)x,y,z的值.
(2)求|x|+|y|+|z|的值. (3)当a=12,b=-4时,求|a+b|-|b|的值练习与巩固:1、绝对值最小的数是___,绝对值等于本身的数是__,平方等于它本身的数有__,立方等于它本身的数有___。
2、下列说法中,正确的有( )
⑴绝对值相等的两个数必相同或互为相反数
⑵正数和零的绝对值等于它本身
⑶只有负数的绝对值是它的相反数
⑷一个数的绝对值必为正。
A、1个 B、2个 C、3个 D、4个
3、若|x-5|+ |y+3|=0,求2x+3y的值。拓展延伸:1、趣味题:小明参加“趣味数学”选修课,课上老师给了一个问题,小明看了很为难,你能帮他一下吗?a、b互为相反数,c、d互为负倒数,
|m|=2,则 -1+m-cd的值为多少?
2、满足|a-b|= |a|+|b|成立的条件是( )
A、ab>0 B、 ab>1 C、ab≤0 D、ab≤ 1 本章难点1、有关零:(1)零既不是正数也不是负数,零大于负数,正数大于零。(2)零的相反数是它本身,零的绝对值是它本身,零的任何非零次幂是零。(3)零是绝对值最小的有理数。(4)零乘以任何数为零,零除以任何不为零的数为零。(5)零没有倒数,零不能做除数。2、有理数中的最值(1) 最小的自然数
(2) 最大的负整数
(3) 绝对值最小的有理数
(4) 平方最小的有理数1 – 100有理数的形式含绝对值的式子的化简|a|=3,|b|=4,求a-b的值分类讨论思想有关乘方的习题
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
