第7章 一次函数的复习

课件39张PPT。 一次函数综合复习课复习 在某个变化过程中,有两个变量x和y,如果给定一个x值,相应地就确定一个y值,那么我们称y是x的函数,其中x是自变量,y是因变量.什么叫函数?
指出下列各式子中的自变量,
因变量,常量,函数.
(1)C＝2πr (r≥0)，
(2)s＝60t (t≥0)，
(3)S＝(n－2)×180 ，
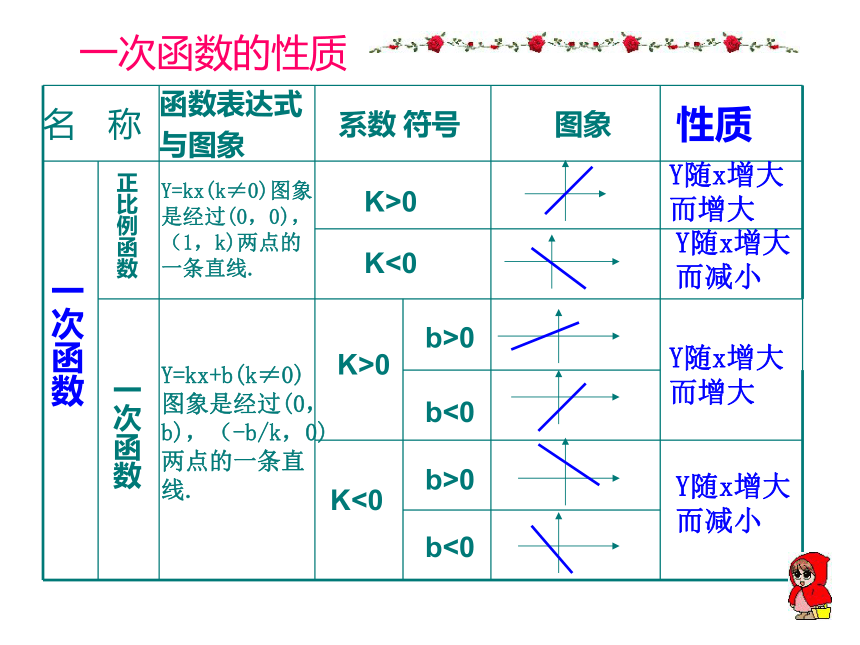
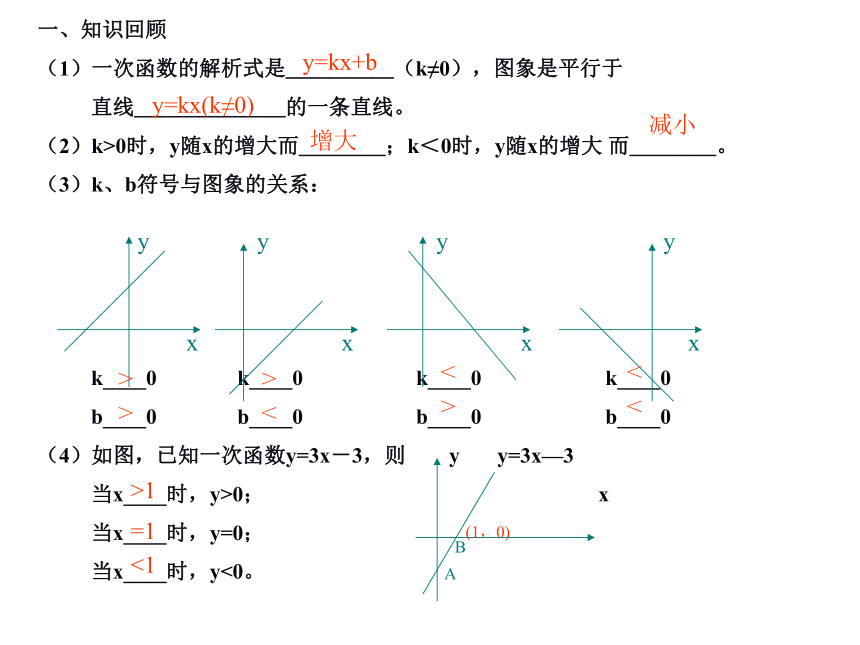
看谁做的快！某市出租车起步价是7元（路程小于或等于3千米），超过3千米每增加1千米加收1.2元。１、你能写出出租车车费y（元）与行程x（千米）之间的函数关系式吗２、李老师乘车８千米，应付多少车费？请你动手写一写！一次函数的性质一次函数正比例函数一次函数Y=kx(k≠0)图象是经过(0，0)，（1，k)两点的一条直线.K>0K<0K>0K<0Y=kx+b(k≠0)图象是经过(0，b)，（-b/k，0)两点的一条直线.b>0b<0b<0b>0Y随x增大而增大Y随x增大而减小Y随x增大而增大Y随x增大而减小一、知识回顾
（1）一次函数的解析式是＿＿＿＿＿（k≠0），图象是平行于
直线＿＿＿＿＿＿＿的一条直线。
（2）k>0时，y随x的增大而＿＿＿＿；k＜0时，y随x的增大 而＿＿＿＿。
（3）k、b符号与图象的关系：


k____0 k____0 k____0 k____0
b____0 b____0 b____0 b____0
（4）如图，已知一次函数y=3x－3，则 y y=3x—3
当x____时，y>0； x
当x____时，y=0；
当x____时，y<0。 y y y y x x x xy=kx+by=kx(k≠0)增大减小＞
＞＞
＜＜
＞＜
＜(1，0) BA>1<1=1例1 已知一次函数(1) k为何值时,它的图象经过原点(2)k 为何值时,它的图象经过点(0, -2)(3)k 为何值时,它的图象平行直线 y= - x(4) k为何值时,它的图象向下平移后,
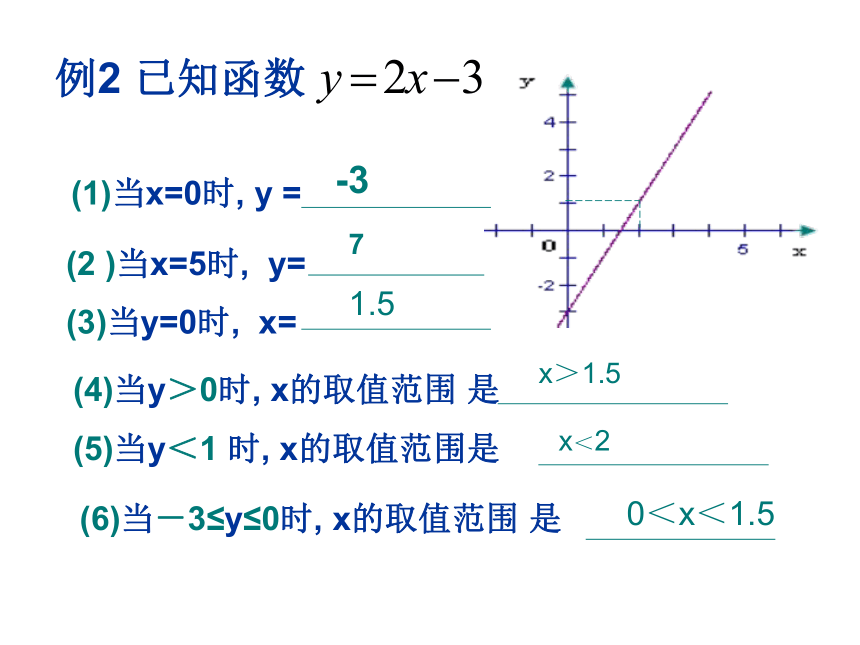
变成直线y=2x+8(5)k 为何值时, y随x的增大而减小二、应用举例：例2 已知函数(1)当x=0时, y =(2 )当x=5时, y=
(3)当y=0时, x=
(4)当y＞0时, x的取值范围 是(6)当－3≤y≤0时, x的取值范围 是(5)当y＜1 时, x的取值范围是-371.5x＞1.5x＜20＜x＜1.5
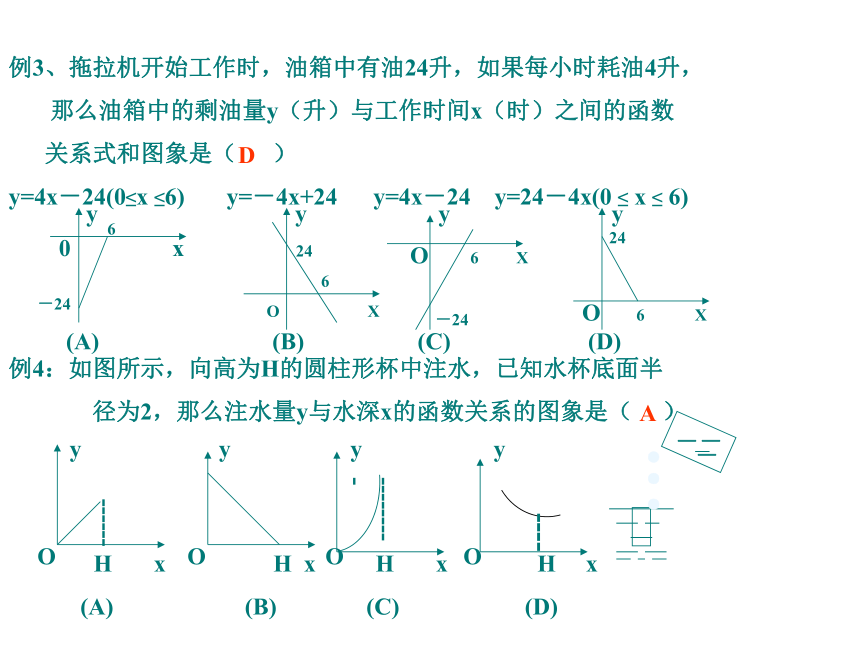
例3、拖拉机开始工作时，油箱中有油24升，如果每小时耗油4升，
那么油箱中的剩油量y（升）与工作时间x（时）之间的函数
关系式和图象是（ ）
y=4x－24(0≤x ≤6) y=－4x+24 y=4x－24 y=24－4x(0 ≤ x ≤ 6)
例4：如图所示，向高为H的圆柱形杯中注水，已知水杯底面半
径为2，那么注水量y与水深x的函数关系的图象是（ ）
y y y y
6
－240 x 24
6
O X O 6 X
－2424O 6 XD(A) (B) (C) (D)------------------- y y y y－－－●●
●O O O O H x H x H x H x(A) (B) (C) (D)A例5、旅客乘车按规定可随身携带一定重量的行李，如果超过规定，则需购行李票，该行李费y（元），行李重量x（kg）的一次函数，如图所示。
求：（1）y与x之间的函数关系式；
（2）旅客最多可免费携带多少
行李的重量。-------------------------------------------y(元)x(kg)9060105O
解：（1）设一次函数关系式为y=kx＋b（k≠0）把x＝60，y＝5和x＝90，y＝10代入得5=60k＋b
10=90k＋b（2）当y＝0时，x＝30∴旅客最多可免费携带的行李重量是30kg 。
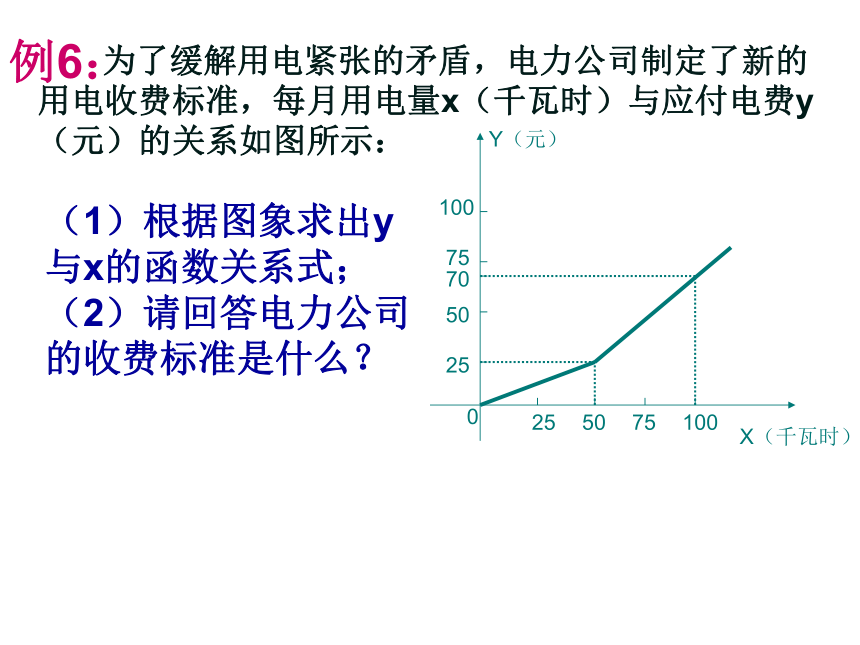
（x≥30）例6： 为了缓解用电紧张的矛盾，电力公司制定了新的用电收费标准，每月用电量x（千瓦时）与应付电费y（元）的关系如图所示：（1）根据图象求出y与x的函数关系式；
（2）请回答电力公司的收费标准是什么？求直线y=2x-1与两坐标轴所围成的三角形面积y=2x-1 -1?解：（如图）∵当x=0时，y=-1 ∴ y=2x-1与y轴的交点为（0,-1) ∵当y=0时，x=?∴ y=2x-1与x轴的交点为(?,0)
= 1/4 ∴AO=? ,BO=1∴SΔAB0= ?·AO·BO = ?×?×1答：直线y=2x-1与两坐标轴所围成的三角形面积为1/4。 B A例7直线y=kx+3与两坐标轴所围成的三角形面积为9，求k的值y=kx+3 -3/k3解:（如图）∵当x=0时，y=3 ∴ y=kx+3与y轴的交点为（0,3) ∵当y=0时，x=-3/k∴ y=kx+3与x轴的交点为(-3/k,0)
∴ k=-1/2或k=1/2∴SΔAB0= ?·AO·BO=9 ?×3×|-3/k|=9答：k的值为-1/2或1/2 。 B A∴AO=3 ,BO=|-3/k|1、已知一次函数y=kx+b,y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( )
(A) (B) （C） （D）A练一练　
2、填空题：
(1)　有下列函数：①　　　　　 , ②　　　　 ,
③　　　 , ④ 。其中过原点的直
线是_____；函数y随x的增大而增大的是___________；函数y随x的增大而减小的是______；图象在第一、二、三象限的是_____。②①、②、③④③ (2) 已知y-1与x成正比例，且x=－2时，y=4，那么y与
x之间的函数关系式为_________________。
www.czsx.com.cn4、在函数 中，自变量x的取值范围是
　　　　　　　　．
5、函数 中，自变量x的取值范围是
　　　　　　　　． 3、在函数 y= -2x+3 中，自变量x的取值范围是
　　　　　　　　． X为全体实数X≠2的实数
X≤3的实数
7、如果方程组
则一次函数y=-2x+4与一次函数y=1－x
的交点为__________8、若两个一次函数 y=x+ 1与y=2x—1的图
象有交点(2，3)，则方程组
的解是___________6、将二元一次方程3x-2y=l化为y是x的一次函数是______y =1.5x-0.5(3,-2){
X=2Y=310、若函数y=kx+b(k,b为常数)的图象如图所示，那么,当y﹥0时，x的取值范围是(　　　)
A、x﹥1　B、x﹥2　C、x﹤1　D、x﹤211、已知一次函数y=kx+b的图象如图所示，当x＜0时，y的取值范围是（ ）
A．y＞0 B、y＜0
C、－2＜y＜0 D．y＜－216、在函数y=2x+3中，当自变量x满足______时，图象在第一象限．DDx﹥012、 一次函数 Y=3x+b 的图象与两坐标轴围成的三角形的面积为48,求b的值.13、 设点P(3,m),Q(n,2)都在函数y=x+b的图象上,
求m+n的值.14、点P(x，y)在第一象限，且x+y=10，点A的坐标为（8，0），设△OPA的面积为S。
用含x的解析式表示S，写出x的取值范围，画出函数S的图象。·A·8PB即S=4y∵x+y=10∴ y=10-x ∴ 这个函数的解析式为S=-4x+40 解:(1)依题意得右图∴ S=4(10-x)(0 (1)求5张白纸黏合后的长度.
(2)设x张白纸黏合后的总长度为ycm,写出y与x之间的函数关系.练习16、某面包厂现年产值是15万元,计划今每年增加2万元,
(1)写出年产值Y(万元)与年数x之间的函数关系式;
(2)画出函数图象;
(3)求5年后的年产值.17、如图，已知A地在B地正南方3千米处，甲乙两人同时分别从A、B两地向正北方向匀速直行，他们与A地的距离S（千米）与所行的时间t（小时）之间的函数关系图象如图所示的AC和BD给出.
(1)当他们行走3小时后，他们之间的距离
为 千米.
(2)当他们之间的距离为
9千米时,他们行走了
小时18、一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图所示,结合图象回答下列问题.
(1)农民自带的零钱是多少?
(2)试求降价前y与x之间的关系式
(3)由表达式你能求出降价前
每千克的土豆价格是多少?
(4)降价后他按每千克0.4元
将剩余土豆售完,这时他手中
的钱(含备用零钱)是26元,
试问他一共带了多少千克土豆?www.czsx.com.cn19、某地市话收费标准为：通话时间在三分钟以内（包括三分钟），话费为每分钟0.6元；通话时间超过了三分钟，超过部分按每分钟0.2元。则总话费y（元）与通话时间x（取整）之间的关系式为 ：20、某音像社对外出租光盘的收费方法是：每张光盘在出租头两天每天收0.8元，以后每天收0.5元，那么，一张光盘在出租后第n天（n是大于2的整数），应收租金y=__________.21、一次函数y=k1x-4与正比例函数y=k2x的图象经过点（2，-1），
（1）分别求出这两个函数的表达式；
（2）求这两个函数的图象与x轴围成的三角形的面积。
（1）旧的电费收费标准中电费 = 每千瓦时电价×用电量，电费调整前连续两个月的电费开支如下表，若该家庭第一季度用电125千瓦时，求该季度的电费走近生活中的函数 （2）电费调整后每月用电量x千瓦时与应付电
费y元的关系如图，若电费调整后某月该家庭用电
65千瓦时，求该月的电费www.czsx.com.cn（3）试问该家庭每月用电多少千瓦时用新标准比用旧标准合算。走进生活中的函数（1）慢车比快车早出发 小时，
快车比慢车早 小时到达B地（2）快车追上慢车时行驶了
_______千米（3）慢车速度为 快车速
度为_______（4）图中快车离开A地的路程y与时间x的函数解
析式 为____________________2427646千米/时69千米/时Y = 69x - 1383、某商店售货时，在进价基础上加一定利润，销量
x（千克）与y（元）如下表所示：判断变量x、y是否满足一次函数关系式，如果是求
出解析式并求当销量为2.5千克时的售价。 4、 刘强的爸爸带回一张电信营业厅的资费表，上面有A、B、C三种新的手机计费标准（打电话收费，接电话不收费）（1）刘强爸爸办公室陈、秦、赵三位叔叔每月打电
话约40分钟，75分钟，200分钟请算算哪种卡便
宜实践与探究5、在一次蜡烛燃烧试验中，甲、乙两根蜡烛燃烧时剩余部分的高度y（厘米）与燃烧时间x（小时）之间的关系如图10所示，请根据图象所提供的信息解答下列问题：
（1）甲、乙两根蜡烛燃烧前的高度分别是 ，从点燃到燃尽所用的时间分别是 。（2）分别求甲、乙两根蜡烛燃烧时y与x之间的函数关系式；
（3）燃烧多长时间时，甲、乙两根蜡烛的高度相等（不考虑都燃尽时的情况）？
在什么时间段内，甲蜡烛比乙蜡烛高？
在什么时间段内，甲蜡烛比乙蜡烛低？
30cm25cm2时2.5时y甲=-15x+30
y乙=-10x+25
x=1x>1x<16、某洗衣机在洗涤衣服时，经历了进水、清洗、排水、脱水四个连续过程，其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示：
根据图象解答下列问题：
(1)洗衣机的进水时间是多少分钟？
(2)清洗时洗衣机中的水量是多少升？
(3)已知洗衣机的排水速度为每分钟19升，
①求排水时y与x之间的关系式。
②如果排水时间为2分钟，求排水
结束时洗衣机中剩下的水量。4分钟40升y= -19x+3252升7、某医药研究所开发了一种新药，在实际验药时发现，如果成人按规定剂量服用，那么每毫升血液中含药量y（毫克）随时间x（时）的变化情况如图所示，当成年人按规定剂量服药后。
（1）服药后______时，血液中含药量最高，
达到每毫升_______毫克，接着逐步衰弱。
（2）服药5时，血液中含药量为每毫升____毫克。363（3）当x≤2时y与x之间的函数关系式是_____。
（4）当x≥2时y与x之间的函数关系式是____。
（5）如果每毫升血液中含药量3毫克或3毫克以上
时，治疗疾病最有效，那么这个有效时间范围是___时。.
y=3xy＝-x+81~5 8、某医药研究所开发了一种新药，在试验药效时发现，如果成人按规定剂量服用，那么服药的一定时间内每毫升血液中含药量y（微克）随时间x（时）逐步增加,变化情况如图所示.6 2Ox/时y/微克（1）当x≤2时,y与x之间的函数关系式
是 。
y=3x（3）如果每毫升血液中含药量4微克或4微克以上时在治疗疾病是有效的，那么这个有效时间是多长?

（2）服药后2时，血液中含药量最高达每毫升6微克，接着每小时逐步衰减 微克。

求出当x≥2时y与x之间的函数关系式.
10、如图为甲、乙两名选手在一次自行车越野赛中，路程y（千米）随时间x（分）变化的图象（全程）．根据图象回答下列问题：
（１）比赛开始多少时间时，两人第一次相遇？
（２）这次比赛全程是多少千米？
（３）比赛开始多少时间时，两人第二次相遇？