6.3 线段的长短比较课件
图片预览


文档简介
课件10张PPT。数缺形时少直观,形缺数时少入微——华罗庚6.3线段长短的比较学习目标:
1、理解线段中点的概念
2、会用刻度尺画线段中点
3、会进行线段和、差、倍、分的简单计算
4、通过实例体验两点之间线段最短的性质,理解两点
之间的距离的概念
学习重点:线段中点的概念和两点之间线段最短的性质
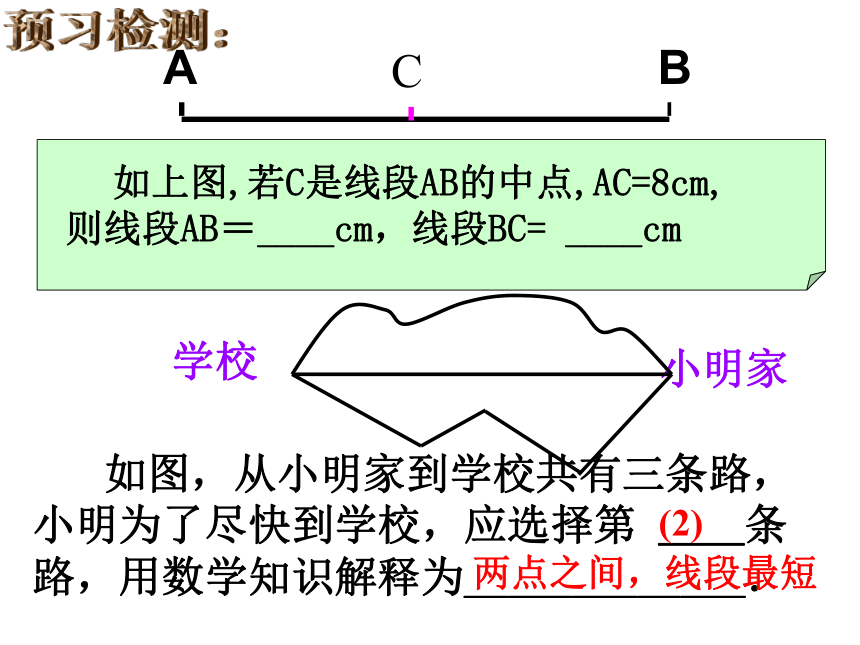
学习难点:线段的运算和表示预习检测: 如上图,若C是线段AB的中点,AC=8cm,
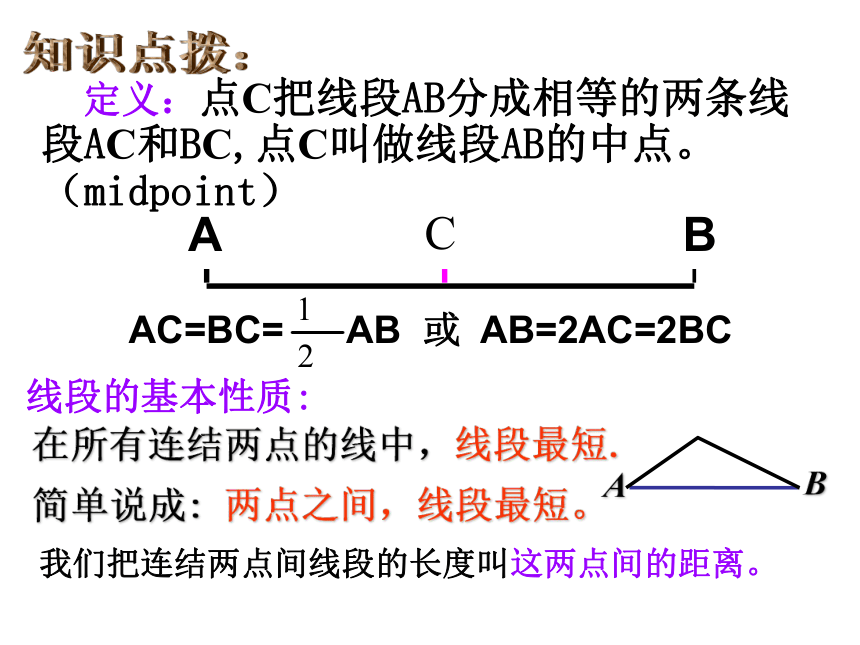
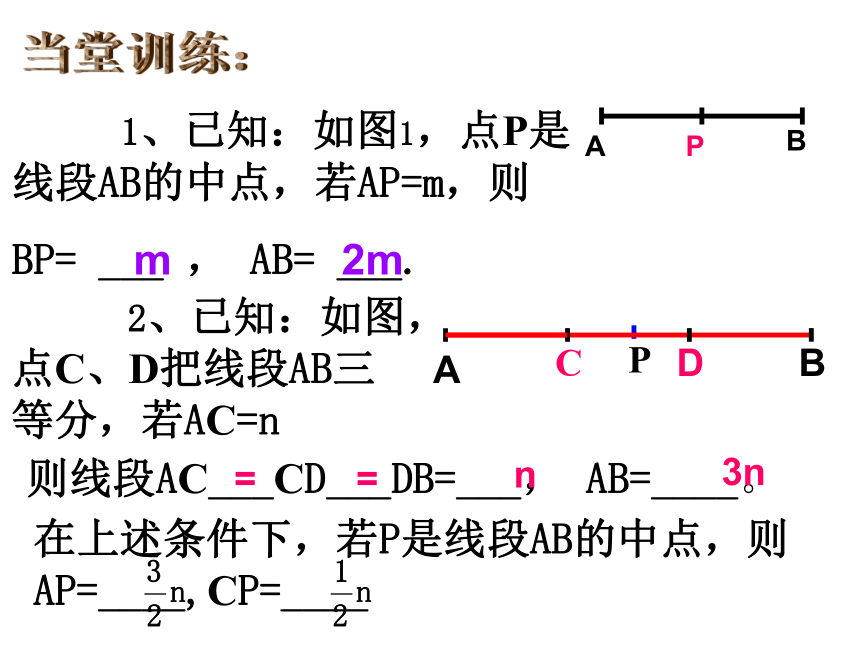
则线段AB=____cm,线段BC= ____cmC 如图,从小明家到学校共有三条路,小明为了尽快到学校,应选择第 __条路,用数学知识解释为_____________.(2)两点之间,线段最短小明家学校 定义:点C把线段AB分成相等的两条线段AC和BC,点C叫做线段AB的中点。(midpoint)知识点拨:CAC=BC= ABAB=2AC=2BC或 在所有连结两点的线中,线段最短. 简单说成: 两点之间,线段最短。线段的基本性质:我们把连结两点间线段的长度叫这两点间的距离。当堂训练: 1、已知:如图1,点P是 线段AB的中点,若AP=m,则
BP= ___ , AB= ___.m2m 2、已知:如图,点C、D把线段AB三等分,若AC=n则线段AC___CD___DB=___, AB=____。在上述条件下,若P是线段AB的中点,则AP=____,CP=____==n3n当堂训练:3、如图,点P是线段AB的中点,点C、D把线段AB三等分。已知线段CP= 1.5cm,求线段AB的长。 4、如图,点C、B、M在线段AN上,C为AB中点,M为BN中点,AC=2cm ,BN=8cm,求CM的长。AAN拓展延伸: 已知线段AB=a ,延长BA至点C使 AC= 。点D为线段BC的中点。
(1)求CD的长
(2)若AD= 3 cm ,求AB的长CDa 如图,有一只蚂蚁,沿长方体的表面一端爬到另一端,怎样画出最短的路线?AB拓展延伸:今天你有什么收获?教学反思:
1、本节课的关键在“两点之间线段最短”的理解,
及线段长度的计算。
2、 “两点之间线段最短”在空间图形中的应用
1、理解线段中点的概念
2、会用刻度尺画线段中点
3、会进行线段和、差、倍、分的简单计算
4、通过实例体验两点之间线段最短的性质,理解两点
之间的距离的概念
学习重点:线段中点的概念和两点之间线段最短的性质
学习难点:线段的运算和表示预习检测: 如上图,若C是线段AB的中点,AC=8cm,
则线段AB=____cm,线段BC= ____cmC 如图,从小明家到学校共有三条路,小明为了尽快到学校,应选择第 __条路,用数学知识解释为_____________.(2)两点之间,线段最短小明家学校 定义:点C把线段AB分成相等的两条线段AC和BC,点C叫做线段AB的中点。(midpoint)知识点拨:CAC=BC= ABAB=2AC=2BC或 在所有连结两点的线中,线段最短. 简单说成: 两点之间,线段最短。线段的基本性质:我们把连结两点间线段的长度叫这两点间的距离。当堂训练: 1、已知:如图1,点P是 线段AB的中点,若AP=m,则
BP= ___ , AB= ___.m2m 2、已知:如图,点C、D把线段AB三等分,若AC=n则线段AC___CD___DB=___, AB=____。在上述条件下,若P是线段AB的中点,则AP=____,CP=____==n3n当堂训练:3、如图,点P是线段AB的中点,点C、D把线段AB三等分。已知线段CP= 1.5cm,求线段AB的长。 4、如图,点C、B、M在线段AN上,C为AB中点,M为BN中点,AC=2cm ,BN=8cm,求CM的长。AAN拓展延伸: 已知线段AB=a ,延长BA至点C使 AC= 。点D为线段BC的中点。
(1)求CD的长
(2)若AD= 3 cm ,求AB的长CDa 如图,有一只蚂蚁,沿长方体的表面一端爬到另一端,怎样画出最短的路线?AB拓展延伸:今天你有什么收获?教学反思:
1、本节课的关键在“两点之间线段最短”的理解,
及线段长度的计算。
2、 “两点之间线段最短”在空间图形中的应用
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
