4.5 相似三角形的性质及其应用(2) 课件(共18张PPT)
文档属性
| 名称 | 4.5 相似三角形的性质及其应用(2) 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-21 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
浙教版九年级上册
4.5 相似三角形的性质及其应用(2)
第四章 相似三角形
在8×8的正方形网格中,△ABC∽△A’B’C’ ,探究下面 的问题:
1、两个相似三角形的相似比是多少?
2、两个相似三角形的周长比是多少?
3、两个相似三角形的面积比是多少?
4、两个相似三角形的周长之比与相似比有什么关系?面积之比与相似比有什么关系?
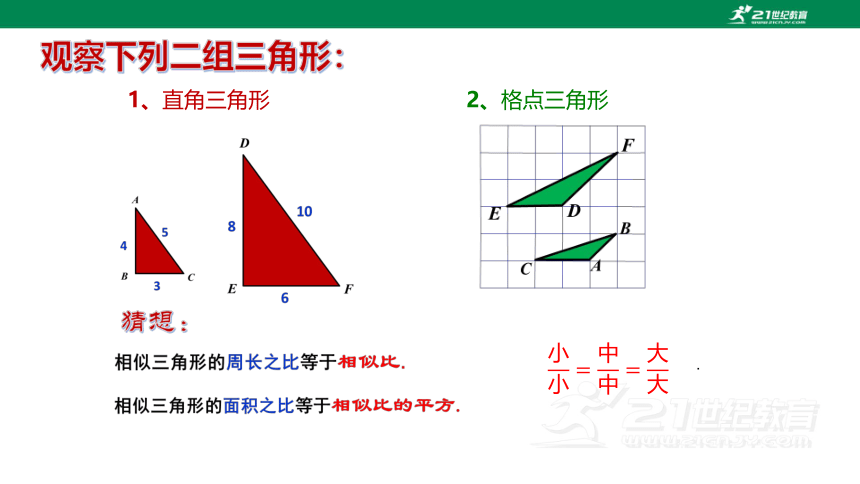
相似三角形的周长比等于相似比,
面积比等于相似比的平方
B’
C’
A’
B
A
C
D
∟
D’
∟
温故知新
.
.
( ?)
k>1, 放大;k=1,全等;k<1,缩小
观察下列二组三角形:
1、直角三角形
2、格点三角形
.
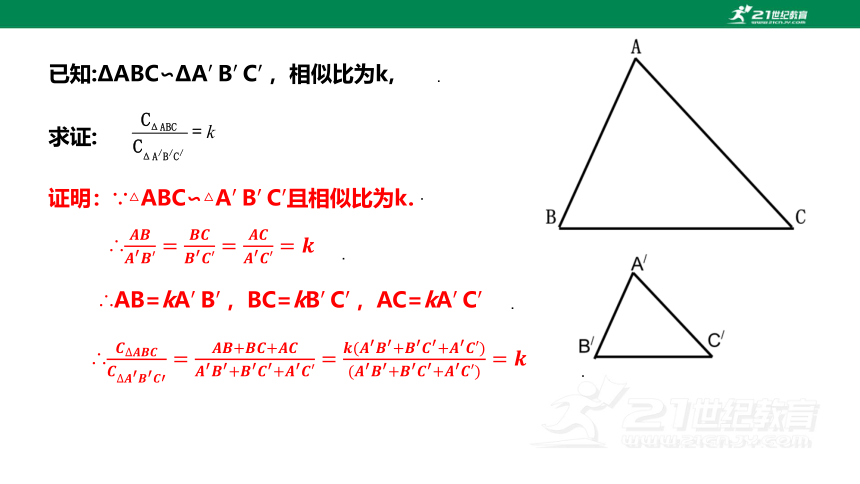
求证:
已知:ΔABC∽ΔABC,相似比为k,
.
证明:∵△ABC∽△ABC且相似比为k.
.
∴
.
∴AB=kAB,BC=kBC,AC=kAC
.
∴
.
已知:ΔABC∽ΔABC,相似比为k,
.
求证:
证明:作BC、BC边上的高AD、AD
.
∵△ABC∽△ABC
.
∴
.
∴
.
相似三角形的对应边上的高之比等于相似比
相似三角形的周长比等于相似比;
相似三角形的面积比等于相似比的平方
几何语言:
∵△ABC∽△A’B’C’,相似比为k,
相似三角形的性质:
∴,
.
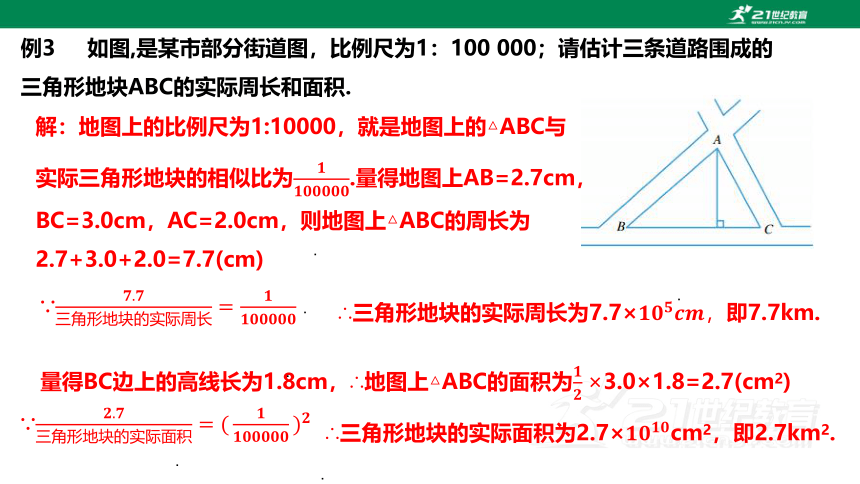
例3 如图,是某市部分街道图,比例尺为1:100 000;请估计三条道路围成的三角形地块ABC的实际周长和面积.
解:地图上的比例尺为1:10000,就是地图上的△ABC与实际三角形地块的相似比为.量得地图上AB=2.7cm,BC=3.0cm,AC=2.0cm,则地图上△ABC的周长为2.7+3.0+2.0=7.7(cm)
.
∴三角形地块的实际面积为2.7×cm2,即2.7km2.
.
∵
.
∴三角形地块的实际周长为7.7×即7.7km.
.
量得BC边上的高线长为1.8cm,∴地图上△ABC的面积为3.0×1.8=2.7(cm2)
.
∵
.
例4 如图,在△ABC中,作DE//BC,分别交AB,AC于点D,E.若要使△ADE与四边形DBCE的面积相等,问AD与AB的比应取多少?
解:∵DE//BC
∴△ADE∽△ABC
由=1,
.
得.
.
∴.
.
∴.
.
答:若△ADE与四边形DBCE的面积相等,则AD与AB的比为.
.
相似三角形的面积比等于相似比的平方
1、已知两个三角形相似,请完成下列表格.
相似比 3
周长比
面积比 10000
m2(m>0)
k(k>0)
2
夯实基础,稳扎稳打
3
9
.
2
100
100
m
m
.
.
2.在10倍的放大镜下看到的三角形与原三角形相比,
三角形的边长,周长,面积,角,哪些放大为10倍
答:三角形的边长,周长放大为10倍.
三角形的面积放大为100倍.
三角形的角大小不变.
3、如图,D,E分别是AB,AC边上的点,∠ADE=∠B, AG⊥BC于点G,AF⊥DE于点F,若AD=3,AB=5 .求:
(1) AF: AG = .
(2)△ADE与△ABC的周长之比 = .
(3)△ADE与△ABC的面积之比= .
3:5
3:5
9:25
4.如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,
DE∥BC,DF∥AC.已知 ,△ABC的面积为a.求 DFCE的面积.
A
D
E
B
F
C
C
D
连续递推,豁然开朗
8. 如图,已知△ABC,作一条与BC平行的直线,把△ABC划分成两部分,使划分成的三角形和四边形的面积之比为1:2,可怎样作?如果要使划分成的两部分面积之比为1:n呢?
解 ∵DE∥BC,
∴△ADE∽△ABC,
A
B
C
D
E
=
.
=
.
.
.
AD:DB=1:( -1)
.
=
.
=
.
.
.
AD:DB=1:( -1)
.
P
A
B
C
D
F
E
.
18=2
.
.
18=8
.
S四边形CDFE=
.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
浙教版九年级上册
4.5 相似三角形的性质及其应用(2)
第四章 相似三角形
在8×8的正方形网格中,△ABC∽△A’B’C’ ,探究下面 的问题:
1、两个相似三角形的相似比是多少?
2、两个相似三角形的周长比是多少?
3、两个相似三角形的面积比是多少?
4、两个相似三角形的周长之比与相似比有什么关系?面积之比与相似比有什么关系?
相似三角形的周长比等于相似比,
面积比等于相似比的平方
B’
C’
A’
B
A
C
D
∟
D’
∟
温故知新
.
.
( ?)
k>1, 放大;k=1,全等;k<1,缩小
观察下列二组三角形:
1、直角三角形
2、格点三角形
.
求证:
已知:ΔABC∽ΔABC,相似比为k,
.
证明:∵△ABC∽△ABC且相似比为k.
.
∴
.
∴AB=kAB,BC=kBC,AC=kAC
.
∴
.
已知:ΔABC∽ΔABC,相似比为k,
.
求证:
证明:作BC、BC边上的高AD、AD
.
∵△ABC∽△ABC
.
∴
.
∴
.
相似三角形的对应边上的高之比等于相似比
相似三角形的周长比等于相似比;
相似三角形的面积比等于相似比的平方
几何语言:
∵△ABC∽△A’B’C’,相似比为k,
相似三角形的性质:
∴,
.
例3 如图,是某市部分街道图,比例尺为1:100 000;请估计三条道路围成的三角形地块ABC的实际周长和面积.
解:地图上的比例尺为1:10000,就是地图上的△ABC与实际三角形地块的相似比为.量得地图上AB=2.7cm,BC=3.0cm,AC=2.0cm,则地图上△ABC的周长为2.7+3.0+2.0=7.7(cm)
.
∴三角形地块的实际面积为2.7×cm2,即2.7km2.
.
∵
.
∴三角形地块的实际周长为7.7×即7.7km.
.
量得BC边上的高线长为1.8cm,∴地图上△ABC的面积为3.0×1.8=2.7(cm2)
.
∵
.
例4 如图,在△ABC中,作DE//BC,分别交AB,AC于点D,E.若要使△ADE与四边形DBCE的面积相等,问AD与AB的比应取多少?
解:∵DE//BC
∴△ADE∽△ABC
由=1,
.
得.
.
∴.
.
∴.
.
答:若△ADE与四边形DBCE的面积相等,则AD与AB的比为.
.
相似三角形的面积比等于相似比的平方
1、已知两个三角形相似,请完成下列表格.
相似比 3
周长比
面积比 10000
m2(m>0)
k(k>0)
2
夯实基础,稳扎稳打
3
9
.
2
100
100
m
m
.
.
2.在10倍的放大镜下看到的三角形与原三角形相比,
三角形的边长,周长,面积,角,哪些放大为10倍
答:三角形的边长,周长放大为10倍.
三角形的面积放大为100倍.
三角形的角大小不变.
3、如图,D,E分别是AB,AC边上的点,∠ADE=∠B, AG⊥BC于点G,AF⊥DE于点F,若AD=3,AB=5 .求:
(1) AF: AG = .
(2)△ADE与△ABC的周长之比 = .
(3)△ADE与△ABC的面积之比= .
3:5
3:5
9:25
4.如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,
DE∥BC,DF∥AC.已知 ,△ABC的面积为a.求 DFCE的面积.
A
D
E
B
F
C
C
D
连续递推,豁然开朗
8. 如图,已知△ABC,作一条与BC平行的直线,把△ABC划分成两部分,使划分成的三角形和四边形的面积之比为1:2,可怎样作?如果要使划分成的两部分面积之比为1:n呢?
解 ∵DE∥BC,
∴△ADE∽△ABC,
A
B
C
D
E
=
.
=
.
.
.
AD:DB=1:( -1)
.
=
.
=
.
.
.
AD:DB=1:( -1)
.
P
A
B
C
D
F
E
.
18=2
.
.
18=8
.
S四边形CDFE=
.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
