2.2简单事件的概率(2)课件

课件14张PPT。2.2 简单事件的概率（2）1、 概率定义：在数学中，我们把事件发生的 可能性的大小称为事件发生的概率关键是求事件所有可能的结果总数n
和其中事件Ａ发生的可能的结果m(m ≤n）2、运用公式　　　　　　求概率，
适用什么事件？
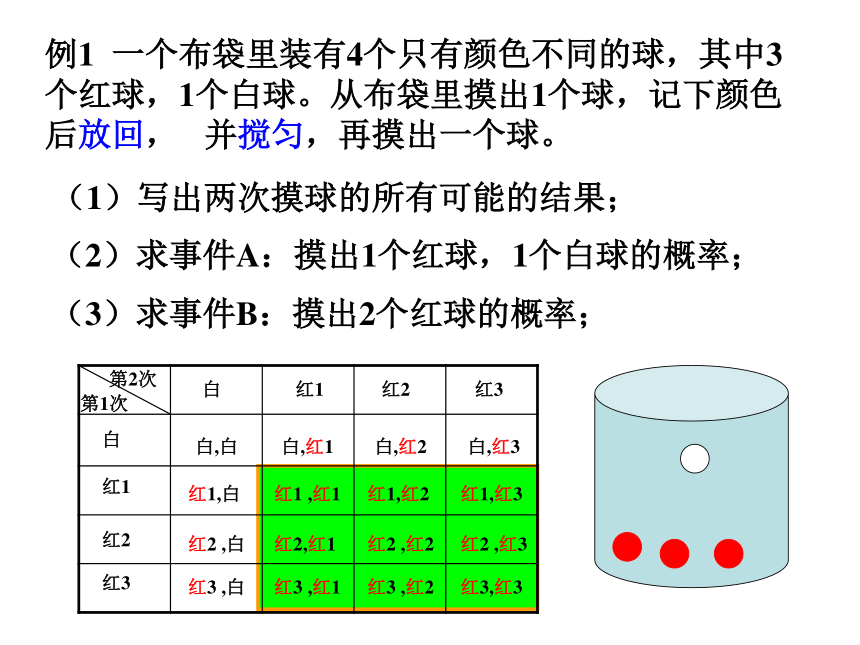
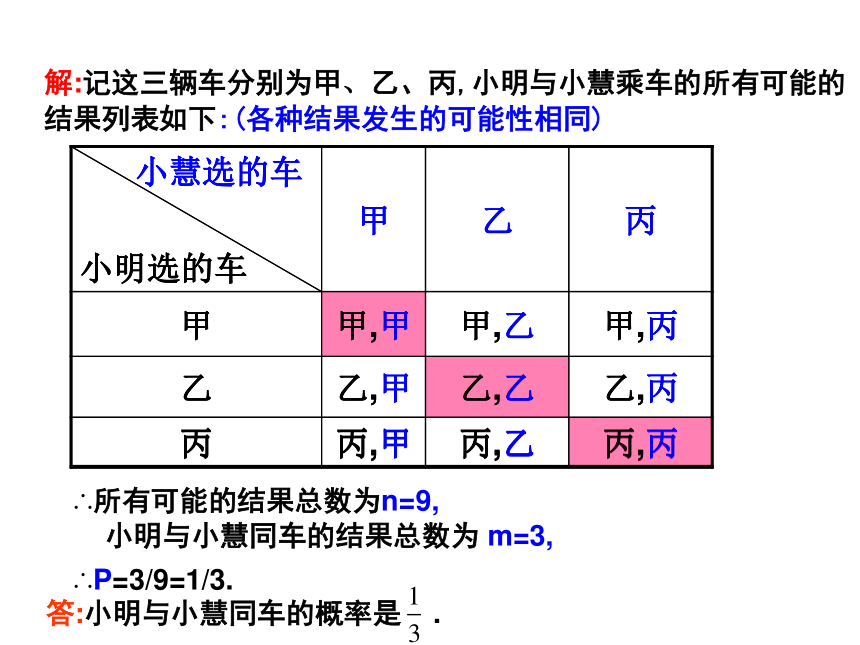
关键是求什么？　　回顾与思考等可能事件例1 一个布袋里装有4个只有颜色不同的球，其中3个红球，1个白球。从布袋里摸出1个球，记下颜色后放回， 并搅匀，再摸出一个球。（2）求事件A：摸出1个红球，1个白球的概率；（3）求事件B：摸出2个红球的概率；第1次第2次（1）写出两次摸球的所有可能的结果；学校组织春游,安排给九年级3辆车,小明与小慧都可以从这3辆车中任选一辆搭乘.问小明与小慧同车的概率有多大?用列表法也试试吧!例2解:记这三辆车分别为甲、乙、丙,小明与小慧乘车的所有可能的
结果列表如下:(各种结果发生的可能性相同)∴所有可能的结果总数为n=9,
小明与小慧同车的结果总数为 m=3,∴P=3/9=1/3.答:小明与小慧同车的概率是 .课内练习：
1．设有5个型号相同的杯子，其中一等品4个，二等品1个。从中任意取1个杯子，记下等级后放回，第二次再从中取1个杯子。求
(1)两次取出都是一等品杯子的概率；
(2)两次取出至少有一次是二等品杯子的概率．2. 有两辆车按1，2编号，李、张两位老师可任意选坐一辆车。求两位老师同坐1号车的概率。例3 如图,转盘的白色扇形和红色扇形的圆心角分别为120°和240°。让转盘自由转动2次,求指针一次落在白色区域,另一次落在红色区域的概率。解:把红色扇形划分成两个圆心角
都是120°的扇形(如图),分别为红Ⅰ,红Ⅱ.让转盘自由转动2次,
所有可能的结果如图所示,且各种结果发生的可能性相同.∴所有可能的结果总数为
n=3x3=9,指针一次落在
白色区域,另一次落在红色
区域的结果总数为m=4.∴P=已知四条线段的长分别是4cm,5cm,6cm,
9cm,则从中任意取三条能构成一个三角形
的概率是多少?课内练习一解:从4条线段中任意取3条,共有4种可能[(4,5,6),(4,5,9)
(4,6,9)(5,6,9)],其中能构成三角形的有3种,因此

P(能构成三角形)= 1654年，有一个法国赌徒梅勒遇到了一个难解的问题：梅勒和他的一个朋友每人出30个金币，两人谁先赢满3局谁就得到全部赌注。在游戏进行了一会儿后，梅勒赢了2局，他的朋友赢了1局。这时候，梅勒由于一个紧急事情必须离开，游戏不得不停止。他们该如何分配赌桌上的60个金币的赌注呢？古怪问题 梅勒的朋友认为，既然他接下来赢的机会是梅勒的一半，那么他该拿到梅勒所得的一半，即他拿20个金币，梅勒拿40个金币。然而梅勒争执道：再掷一次骰子，即使他输了，游戏是平局，他最少也能得到全部赌注的一半30个金币；但如果他赢了，并可拿走全部的60个金币。在下一次掷骰子之前，他实际上已经拥有了30个金币，他还有50%的机会赢得另外30个金币，所以，他应分得45个金币。 后来梅勒把这个问题告诉了当时法国著名的数学家帕斯卡，这居然也难住了帕斯卡，因为当时并没有相关知识来解决此类问题，而且两人说的似乎都有道理。帕斯卡又写信告诉了另一个著名的数学家费马，于是在这两位伟大的法国数学家之间开始了具有划时代意义的通信，在通信中，他们最终正确地解决了这个问题。他们设想：如果继续赌下去，梅勒（设为甲）和他朋友（设为乙）最终获胜的机会如何呢?他们俩至多再赌2局即可分出胜负，这2局有4种可能结果：甲甲、甲乙、乙甲、乙乙。前3种情况都是甲最后取胜，只有最后一种情况才是乙取胜，所以赌注应按3：1的比例分配，即甲得45个金币，乙15个。 用6个颜色不同的乒乓球设计一个摸球游戏.
(1)使摸到白球的概率为 ,摸到黄球和摸到红球
的概率也各为 ;
(2)使摸到白球的概率为 ,摸到黄球的概率为 ,
摸到红球的概率为 ;
(3)使摸到红球和黄球的概率各为 ,摸到白球的概

率为 . 课内练习二用树状图或表格表示概率回 味 无 穷 1、利用树状图或表格可以清晰地表
示出某个事件发生的所有可能出现的
结果;从而较方便地求出某些事件发
生的概率.2 根据不同的情况选择恰当的方法表示某个事件发生的所有可能结果。