4.5 相似三角形的性质及其应用(3) 课件(共16张PPT)
文档属性
| 名称 | 4.5 相似三角形的性质及其应用(3) 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-22 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
浙教版九年级上册
4.5 相似三角形的性质及其应用(3)
第四章 相似三角形
相似三角形的性质:
1、相似三角形对应角相等。
∵⊿ABC∽⊿A′B′C′ ∴ ∠A=∠A′,∠B=∠B′,∠C= ∠C′
2、相似三角形对应边成比例。
∵⊿ABC∽⊿A′B′C′ ∴AB:A′B′=BC :B′C′=CA :C′A′
3、相似三角形的周长之比等于相似比;
4、相似三角形的面积之比等于相似比的平方。
5、相似三角形的对应高线、中线、角平分线之比等于相似比。
三角形的重心分每一条中线成1:2的两条线段。
6.
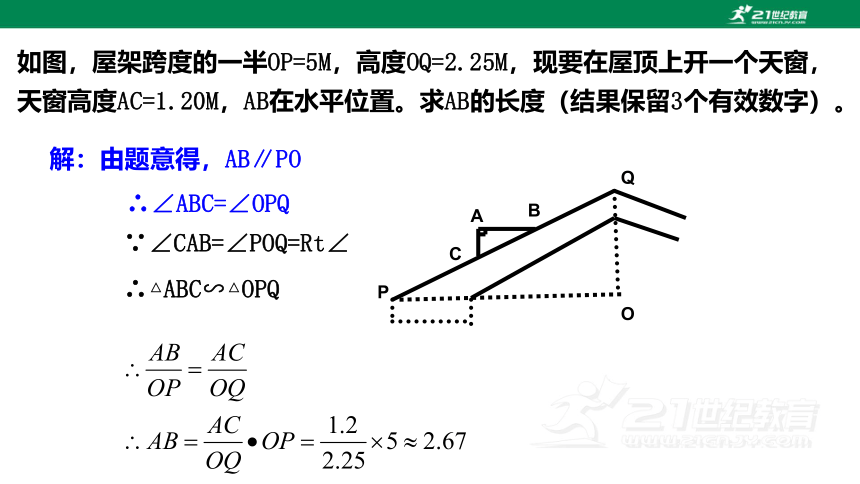
如图,屋架跨度的一半OP=5M,高度OQ=2.25M,现要在屋顶上开一个天窗,天窗高度AC=1.20M,AB在水平位置。求AB的长度(结果保留3个有效数字)。
P
O
Q
A
B
C
解:由题意得,AB∥PO
∴∠ABC=∠OPQ
∵∠CAB=∠POQ=Rt∠
∴△ABC∽△OPQ
怎样利用相似三角形的有关知识测量旗杆的高度
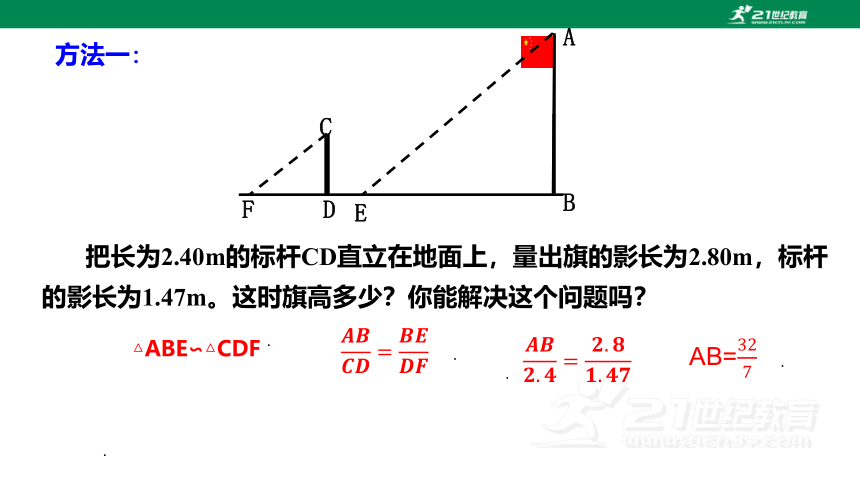
方法一:
A
B
E
C
D
F
把长为2.40m的标杆CD直立在地面上,量出旗的影长为2.80m,标杆的影长为1.47m。这时旗高多少?你能解决这个问题吗?
△ABE∽△CDF
.
.
.
.
AB=
.
方法二:
把一小镜子放在离红旗(AB)8米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到红旗顶点A,再用皮尺量得DE=2.8m,观察者目高CD=1.6m。这时旗高多少?你能解决这个问题吗?
B
E
C
D
A
△ABE∽△CDE
.
.
AB=
.
.
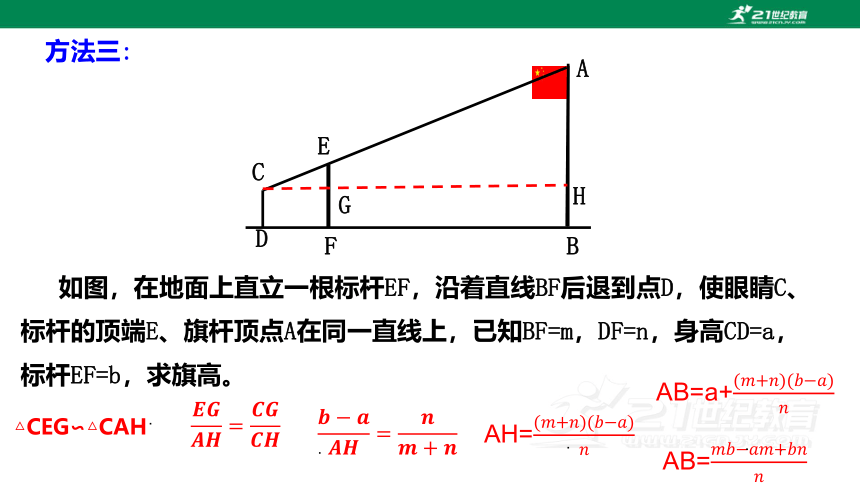
方法三:
如图,在地面上直立一根标杆EF,沿着直线BF后退到点D,使眼睛C、标杆的顶端E、旗杆顶点A在同一直线上,已知BF=m,DF=n,身高CD=a,标杆EF=b,求旗高。
C
D
G
E
F
A
B
△CEG∽△CAH
.
.
AH=
.
AB=a+
.
AB=
.
H
.
1.某一时刻树的影长为8米,同一时刻身高为1.5米的人的影长为3米,则树高为 .
4米
.
h=4
夯实基础,稳扎稳打
2、步枪在瞄准时的示意图如图,从眼睛到准星的距离OE为80cm,步枪上准星宽度AB为2mm,目标的正面宽度CD为50cm,求眼睛到目标的距离OF。
E
A
B
O
C
D
F
准星
A
B
解:由题意得,△OAB∽ △OCD,
AB
CD
OE
OF
0.2
50
80
OF
= ,即 = ,
解得:OF=20000(cm)
=200(m).
3.如图,△ABC是一块锐角三角形余料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为x毫米。
因为PN∥BC,所以△APN∽ △ABC
所以
AE
AD
=
PN
BC
因此 ,得 x=48(毫米)。
80–x
80
=
x
120
N
M
Q
P
E
D
C
B
A
连续递推,豁然开朗
x=16
=
.
4.
∟
G
△ABG∽ △CBE
CE=
.
AG
CE
=
AB
BC
.
AG
=
1.2
2.4
.
AG=
.
AD=+1.4≈2.4 (m)
.
5.
6、如图,正方形城邑DEFG的四面正中各有城门,出北门20步的A处(HA=20步)有一树木,出南门14步到C处(KC=14步),再向西行1775步到B处(CB=1775步),正好看到A处的树木(点D在直线AB上),求城邑的边长。
A
B
C
D
G
E
F
H
K
=
.
x2+34x-71000=0
.
x1=250, x2=-284(舍去)
.
7、在直径为AB的半圆内,划出一个三角形区域,使三角形的一边为AB,顶点C在半圆周上,现要建造一个内接于三角形ABC的矩形水池DEFN,其中DE在AB上,如图设计方案是使AC=8,BC=6,
求(1)三角形AB边上的高线CH。
(2)设DN=x,NF=y,求y关于x的函数解析式。
(3)当x为何值时,水池DEFN的面积最大,最大为多少?
H
G
(2)
(1) 6×8=10×CH ,CH=4.8
0<2.4<4.8
思维拓展,更上一层
=
.
y= - x+10 (0.
(3) S=x ( - x+10 )
.
= - x2+10x
.
x=-
.
S最大=
.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
浙教版九年级上册
4.5 相似三角形的性质及其应用(3)
第四章 相似三角形
相似三角形的性质:
1、相似三角形对应角相等。
∵⊿ABC∽⊿A′B′C′ ∴ ∠A=∠A′,∠B=∠B′,∠C= ∠C′
2、相似三角形对应边成比例。
∵⊿ABC∽⊿A′B′C′ ∴AB:A′B′=BC :B′C′=CA :C′A′
3、相似三角形的周长之比等于相似比;
4、相似三角形的面积之比等于相似比的平方。
5、相似三角形的对应高线、中线、角平分线之比等于相似比。
三角形的重心分每一条中线成1:2的两条线段。
6.
如图,屋架跨度的一半OP=5M,高度OQ=2.25M,现要在屋顶上开一个天窗,天窗高度AC=1.20M,AB在水平位置。求AB的长度(结果保留3个有效数字)。
P
O
Q
A
B
C
解:由题意得,AB∥PO
∴∠ABC=∠OPQ
∵∠CAB=∠POQ=Rt∠
∴△ABC∽△OPQ
怎样利用相似三角形的有关知识测量旗杆的高度
方法一:
A
B
E
C
D
F
把长为2.40m的标杆CD直立在地面上,量出旗的影长为2.80m,标杆的影长为1.47m。这时旗高多少?你能解决这个问题吗?
△ABE∽△CDF
.
.
.
.
AB=
.
方法二:
把一小镜子放在离红旗(AB)8米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到红旗顶点A,再用皮尺量得DE=2.8m,观察者目高CD=1.6m。这时旗高多少?你能解决这个问题吗?
B
E
C
D
A
△ABE∽△CDE
.
.
AB=
.
.
方法三:
如图,在地面上直立一根标杆EF,沿着直线BF后退到点D,使眼睛C、标杆的顶端E、旗杆顶点A在同一直线上,已知BF=m,DF=n,身高CD=a,标杆EF=b,求旗高。
C
D
G
E
F
A
B
△CEG∽△CAH
.
.
AH=
.
AB=a+
.
AB=
.
H
.
1.某一时刻树的影长为8米,同一时刻身高为1.5米的人的影长为3米,则树高为 .
4米
.
h=4
夯实基础,稳扎稳打
2、步枪在瞄准时的示意图如图,从眼睛到准星的距离OE为80cm,步枪上准星宽度AB为2mm,目标的正面宽度CD为50cm,求眼睛到目标的距离OF。
E
A
B
O
C
D
F
准星
A
B
解:由题意得,△OAB∽ △OCD,
AB
CD
OE
OF
0.2
50
80
OF
= ,即 = ,
解得:OF=20000(cm)
=200(m).
3.如图,△ABC是一块锐角三角形余料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为x毫米。
因为PN∥BC,所以△APN∽ △ABC
所以
AE
AD
=
PN
BC
因此 ,得 x=48(毫米)。
80–x
80
=
x
120
N
M
Q
P
E
D
C
B
A
连续递推,豁然开朗
x=16
=
.
4.
∟
G
△ABG∽ △CBE
CE=
.
AG
CE
=
AB
BC
.
AG
=
1.2
2.4
.
AG=
.
AD=+1.4≈2.4 (m)
.
5.
6、如图,正方形城邑DEFG的四面正中各有城门,出北门20步的A处(HA=20步)有一树木,出南门14步到C处(KC=14步),再向西行1775步到B处(CB=1775步),正好看到A处的树木(点D在直线AB上),求城邑的边长。
A
B
C
D
G
E
F
H
K
=
.
x2+34x-71000=0
.
x1=250, x2=-284(舍去)
.
7、在直径为AB的半圆内,划出一个三角形区域,使三角形的一边为AB,顶点C在半圆周上,现要建造一个内接于三角形ABC的矩形水池DEFN,其中DE在AB上,如图设计方案是使AC=8,BC=6,
求(1)三角形AB边上的高线CH。
(2)设DN=x,NF=y,求y关于x的函数解析式。
(3)当x为何值时,水池DEFN的面积最大,最大为多少?
H
G
(2)
(1) 6×8=10×CH ,CH=4.8
0<2.4<4.8
思维拓展,更上一层
=
.
y= - x+10 (0
(3) S=x ( - x+10 )
.
= - x2+10x
.
x=-
.
S最大=
.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
