第四章 相似三角形章末复习-----母子相似型 课件(共20张PPT)
文档属性
| 名称 | 第四章 相似三角形章末复习-----母子相似型 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-26 00:00:00 | ||
图片预览



文档简介
(共20张PPT)
浙教版九年级上册
------------母子型相似
第四章 相似三角形章末复习
相似图形的定义:形状相同的图形叫做相似图形
平行线分线段成比例定理:两条直线被一组平行线所截,所得的对应线段成比例。
相似三角形的判定:
1、平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似
2、三边成比例的两个三角形相似
3、两边成比例且夹角相等的两个三角形相似
4、两角分别相等的两个三角形相似
相似三角形的性质:
1、对应角相等、对应边成比例;
2、对应角平分线的比、对应中线的比、对应高线的比、周长的比等于相似比、
3、面积的比等于相似比的平方
推论:平行三角形一边的直线截其它两边(或两边的延长线),所得的对应线段成比例。
齐声朗读
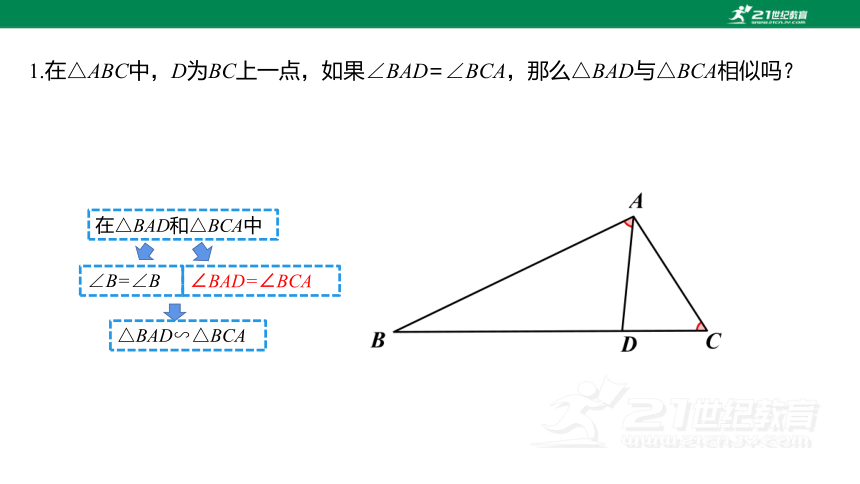
1.在△ABC中,D为BC上一点,如果∠BAD=∠BCA,那么△BAD与△BCA相似吗?
在△BAD和△BCA中
∠B=∠B
∠BAD=∠BCA
△BAD∽△BCA
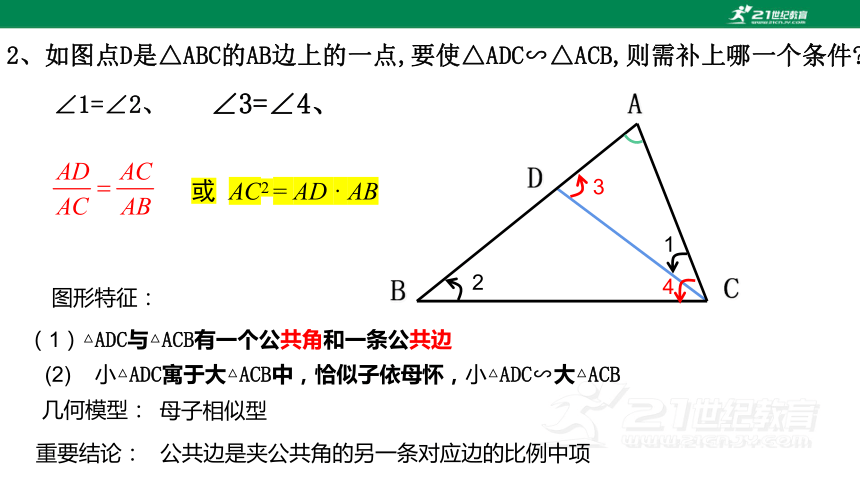
2、如图点D是△ABC的AB边上的一点,要使△ADC∽△ACB,则需补上哪一个条件
A
C
B
D
∠1=∠2、
∠3=∠4、
或 AC2 = AD · AB
1
2
3
4
图形特征:
(1)△ADC与△ACB有一个公共角和一条公共边
(2) 小△ADC寓于大△ACB中,恰似子依母怀,小△ADC∽大△ACB
几何模型:
母子相似型
重要结论:
公共边是夹公共角的另一条对应边的比例中项
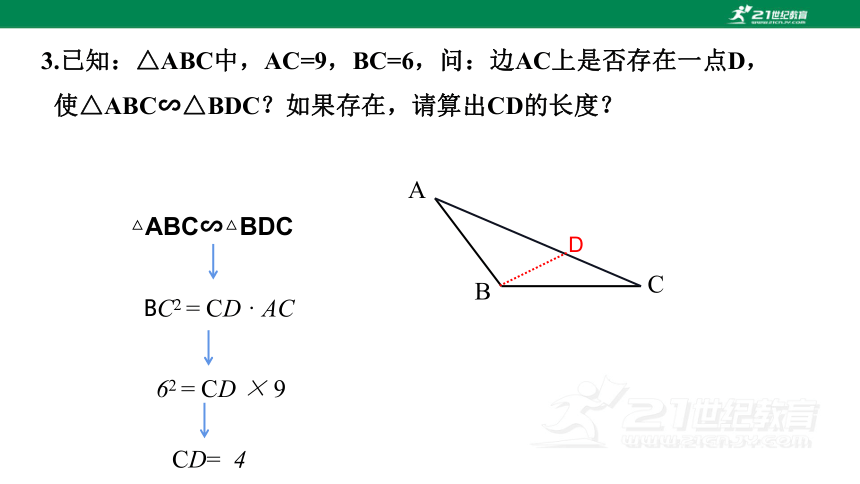
3.已知:△ABC中,AC=9,BC=6,问:边AC上是否存在一点D,
使△ABC∽△BDC?如果存在,请算出CD的长度?
A
B
C
D
△ABC∽△BDC
BC2 = CD · AC
62 = CD × 9
CD= 4
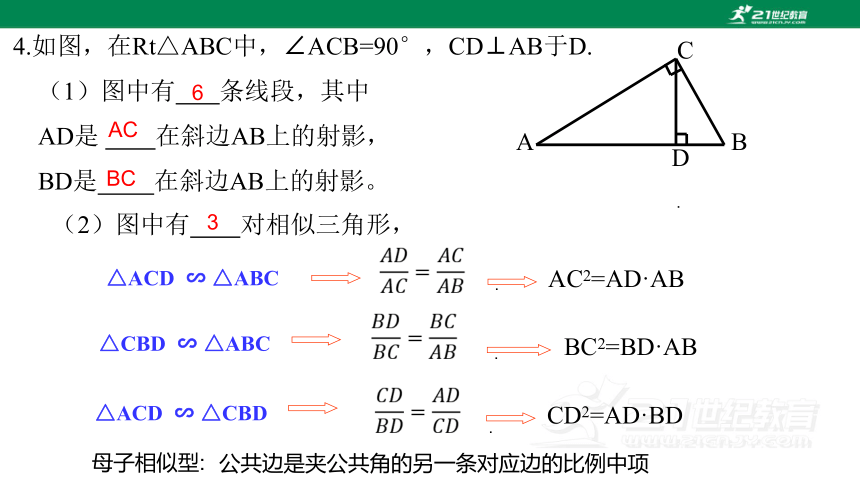
4.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.
A
B
C
D
(1)图中有 条线段,其中
AD是 在斜边AB上的射影,
BD是 在斜边AB上的射影。
6
AC
BC
(2)图中有 对相似三角形,
3
△ACD ∽ △CBD
△ACD ∽ △ABC
△CBD ∽ △ABC
CD2=AD·BD
.
AC2=AD·AB
.
BC2=BD·AB
.
.
公共边是夹公共角的另一条对应边的比例中项
母子相似型:
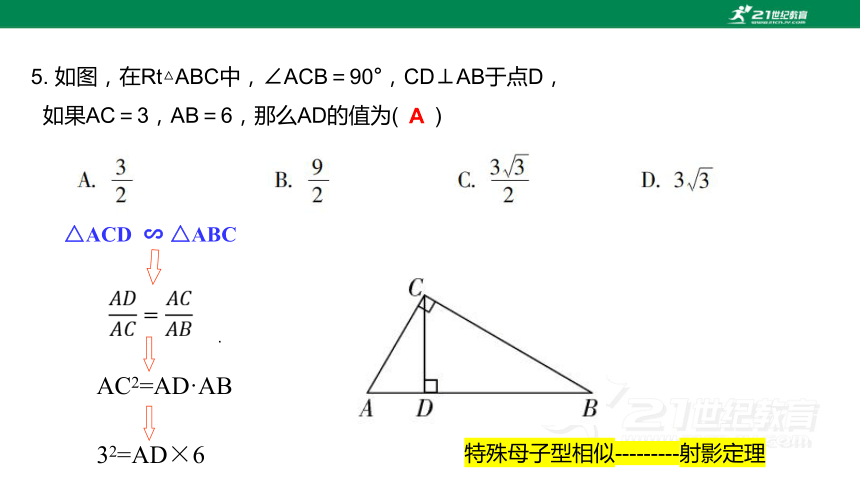
5. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,
如果AC=3,AB=6,那么AD的值为( )
A
△ACD ∽ △ABC
.
AC2=AD·AB
32=AD×6
特殊母子型相似---------射影定理
6.如图,在 △ABC 中,CD 是边 AB 上的高,且 ,求证 :∠ACB=90°.
A
B
C
D
证明: ∵ CD 是边 AB 上的高,
∴ ∠ADC =∠CDB =90°.
∵
∴△ADC ∽△CDB,∴ ∠ACD =∠B,
∴ ∠ACB =∠ACD +∠BCD =∠B +∠BCD = 90°.
母子相似型:
公共边是夹等角的另一条对应边的比例中项
A
B
D
C
B
D
C
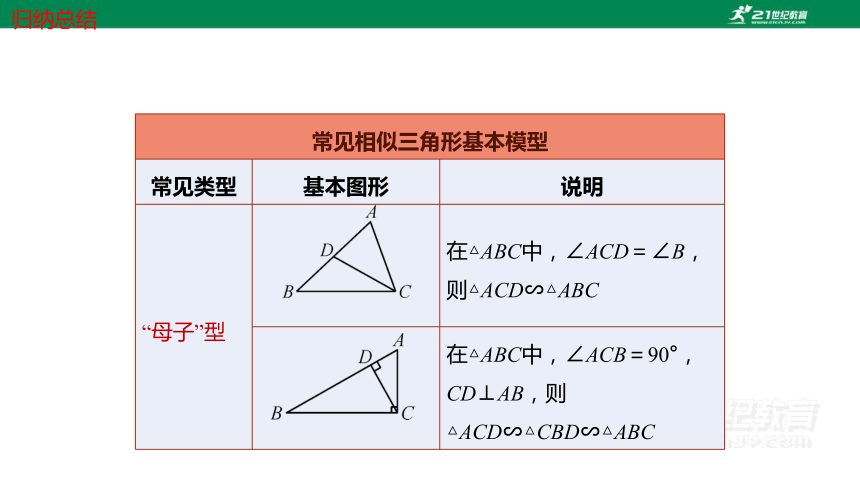
常见相似三角形基本模型 常见类型 基本图形 说明
“母子”型 在△ABC中,∠ACD=∠B,则△ACD∽△ABC
在△ABC中,∠ACB=90°,CD⊥AB,则△ACD∽△CBD∽△ABC
归纳总结
③共边共角
特殊母子型相似---------射影定理
1. 已知:如图,∠ABD=∠C,AD=2, AC=8,求AB.
A
B
C
D
解:∵ ∠ A= ∠ A,∠ABD=∠C,
∴ △ABD ∽ △ACB ,
∴ AB : AC=AD : AB,
∴ AB2 = AD · AC.
∵ AD=2, AC=8,
∴ AB =4.
重点提示:图中找母子
相似得比例
比例来计算
计算求线段
夯实基础,稳扎稳打
2.如图,在△ABC中,点D是AB边上的一点,若
∠ACD=∠B,AD=1,AC=2,△ADC的面积为1,求△BCD的面积
解∵∠ACD=∠B,∠A=∠A,
∴△ACD∽△ABC,∴=()2=.
∵S△ACD=1,∴S△ABC=4,
S△BCD=S△ABC-S△ACD=3.
.
3.如图,AB是半圆O的直径,D,E是半圆上任意两点,连接AD,DE,AE与BD相交于点C,要使△ADC与△ABD相似,可以添加一个条件,下列添加的条件其中错误的是( )
A.∠ACD=∠DAB B.AD=DE
C.AD2=BD·CD D.AD·AB=AC·BD
D
4. 如图,CD 是 ⊙O 的弦,AB 是直径,CD⊥AB,垂
足为 P,求证:PC2 = PA · PB.
·
A
C
D
O
P
证明:连接AC,BC.
∵AB是直径,
∴∠ACB=90°,
∴ ∠A + ∠B = 90°.
又 ∵CD⊥AB,∴∠CPB=90°,
∠PCB+∠B=90°.
又 ∠A=∠CPB,
∴ △APC ∽△CPB.
B
5 :如图,已知A、B是以BD为 直径的⊙O上两点,C为BD上一点,且∠ACB=90 ,AC=3,BC=4.⊙O是否存在这样的点E,使得△BAE 与△BAC
相似.若存在,求AE的长;若不存在,请说明理由.
E
E
(1)
(2)
连续递推,豁然开朗
6.如图,在△ABC中,∠BAC=90°,M为BC的中点,DM⊥BC交CA的延长线于点D,交AB于点E.
求证:AM2=MD·ME.
证明:∵DM⊥BC,∠BAC=90°,
∴∠B+∠BEM=90°,∠D+∠DEA=90°.
∵∠BEM=∠DEA,∴∠B=∠D.
又∵M为BC的中点,∠BAC=90°,∴BM=AM.
∴∠B=∠BAM.∴∠BAM=∠D,即∠EAM=∠D.
又∵∠AME=∠DMA,∴△AME∽△DMA.
∴ ,即AM2=MD·ME.
7. 如图,点C是△ABD的中线AE上一点,且∠EBC=∠EAB,
求证:∠EDC=∠DAC.
分析:
∠EBC=∠EAB
∠BEC=∠AEB
△AEB∽△BEC
AE是△ABD的中线
∠DEC=∠AED
△DEC∽△AED
∠EDC=∠DAC
8. 如图,△ABC中,AB=AC,BD⊥AC于点D,求证:
A
B
C
D
证明:
法一
在AC上取点E,使得CD=ED连接BE.
∵CD=ED,BD⊥AC
∴BE=BC
∴∠BEC=∠BCE.
∵AB=AC. ∴∠ABC=∠ACB.
∴∠ABC=∠BEC.
又∵∠ACB=∠BCE.
∴△ABC∽△BEC.
∴
即 ,
E
思维拓展,更上一层
8. 如图,△ABC中,AB=AC,BD⊥AC于点D,求证:
A
B
C
D
E
法二
延长CA到点E,使得CA=AE,连接BE
AB=AC
AB=AC=CE
∠EBA=∠E,∠ABC=∠C
∠EBC=90°
BD⊥AC
△CDB∽△CBE
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
浙教版九年级上册
------------母子型相似
第四章 相似三角形章末复习
相似图形的定义:形状相同的图形叫做相似图形
平行线分线段成比例定理:两条直线被一组平行线所截,所得的对应线段成比例。
相似三角形的判定:
1、平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似
2、三边成比例的两个三角形相似
3、两边成比例且夹角相等的两个三角形相似
4、两角分别相等的两个三角形相似
相似三角形的性质:
1、对应角相等、对应边成比例;
2、对应角平分线的比、对应中线的比、对应高线的比、周长的比等于相似比、
3、面积的比等于相似比的平方
推论:平行三角形一边的直线截其它两边(或两边的延长线),所得的对应线段成比例。
齐声朗读
1.在△ABC中,D为BC上一点,如果∠BAD=∠BCA,那么△BAD与△BCA相似吗?
在△BAD和△BCA中
∠B=∠B
∠BAD=∠BCA
△BAD∽△BCA
2、如图点D是△ABC的AB边上的一点,要使△ADC∽△ACB,则需补上哪一个条件
A
C
B
D
∠1=∠2、
∠3=∠4、
或 AC2 = AD · AB
1
2
3
4
图形特征:
(1)△ADC与△ACB有一个公共角和一条公共边
(2) 小△ADC寓于大△ACB中,恰似子依母怀,小△ADC∽大△ACB
几何模型:
母子相似型
重要结论:
公共边是夹公共角的另一条对应边的比例中项
3.已知:△ABC中,AC=9,BC=6,问:边AC上是否存在一点D,
使△ABC∽△BDC?如果存在,请算出CD的长度?
A
B
C
D
△ABC∽△BDC
BC2 = CD · AC
62 = CD × 9
CD= 4
4.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.
A
B
C
D
(1)图中有 条线段,其中
AD是 在斜边AB上的射影,
BD是 在斜边AB上的射影。
6
AC
BC
(2)图中有 对相似三角形,
3
△ACD ∽ △CBD
△ACD ∽ △ABC
△CBD ∽ △ABC
CD2=AD·BD
.
AC2=AD·AB
.
BC2=BD·AB
.
.
公共边是夹公共角的另一条对应边的比例中项
母子相似型:
5. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,
如果AC=3,AB=6,那么AD的值为( )
A
△ACD ∽ △ABC
.
AC2=AD·AB
32=AD×6
特殊母子型相似---------射影定理
6.如图,在 △ABC 中,CD 是边 AB 上的高,且 ,求证 :∠ACB=90°.
A
B
C
D
证明: ∵ CD 是边 AB 上的高,
∴ ∠ADC =∠CDB =90°.
∵
∴△ADC ∽△CDB,∴ ∠ACD =∠B,
∴ ∠ACB =∠ACD +∠BCD =∠B +∠BCD = 90°.
母子相似型:
公共边是夹等角的另一条对应边的比例中项
A
B
D
C
B
D
C
常见相似三角形基本模型 常见类型 基本图形 说明
“母子”型 在△ABC中,∠ACD=∠B,则△ACD∽△ABC
在△ABC中,∠ACB=90°,CD⊥AB,则△ACD∽△CBD∽△ABC
归纳总结
③共边共角
特殊母子型相似---------射影定理
1. 已知:如图,∠ABD=∠C,AD=2, AC=8,求AB.
A
B
C
D
解:∵ ∠ A= ∠ A,∠ABD=∠C,
∴ △ABD ∽ △ACB ,
∴ AB : AC=AD : AB,
∴ AB2 = AD · AC.
∵ AD=2, AC=8,
∴ AB =4.
重点提示:图中找母子
相似得比例
比例来计算
计算求线段
夯实基础,稳扎稳打
2.如图,在△ABC中,点D是AB边上的一点,若
∠ACD=∠B,AD=1,AC=2,△ADC的面积为1,求△BCD的面积
解∵∠ACD=∠B,∠A=∠A,
∴△ACD∽△ABC,∴=()2=.
∵S△ACD=1,∴S△ABC=4,
S△BCD=S△ABC-S△ACD=3.
.
3.如图,AB是半圆O的直径,D,E是半圆上任意两点,连接AD,DE,AE与BD相交于点C,要使△ADC与△ABD相似,可以添加一个条件,下列添加的条件其中错误的是( )
A.∠ACD=∠DAB B.AD=DE
C.AD2=BD·CD D.AD·AB=AC·BD
D
4. 如图,CD 是 ⊙O 的弦,AB 是直径,CD⊥AB,垂
足为 P,求证:PC2 = PA · PB.
·
A
C
D
O
P
证明:连接AC,BC.
∵AB是直径,
∴∠ACB=90°,
∴ ∠A + ∠B = 90°.
又 ∵CD⊥AB,∴∠CPB=90°,
∠PCB+∠B=90°.
又 ∠A=∠CPB,
∴ △APC ∽△CPB.
B
5 :如图,已知A、B是以BD为 直径的⊙O上两点,C为BD上一点,且∠ACB=90 ,AC=3,BC=4.⊙O是否存在这样的点E,使得△BAE 与△BAC
相似.若存在,求AE的长;若不存在,请说明理由.
E
E
(1)
(2)
连续递推,豁然开朗
6.如图,在△ABC中,∠BAC=90°,M为BC的中点,DM⊥BC交CA的延长线于点D,交AB于点E.
求证:AM2=MD·ME.
证明:∵DM⊥BC,∠BAC=90°,
∴∠B+∠BEM=90°,∠D+∠DEA=90°.
∵∠BEM=∠DEA,∴∠B=∠D.
又∵M为BC的中点,∠BAC=90°,∴BM=AM.
∴∠B=∠BAM.∴∠BAM=∠D,即∠EAM=∠D.
又∵∠AME=∠DMA,∴△AME∽△DMA.
∴ ,即AM2=MD·ME.
7. 如图,点C是△ABD的中线AE上一点,且∠EBC=∠EAB,
求证:∠EDC=∠DAC.
分析:
∠EBC=∠EAB
∠BEC=∠AEB
△AEB∽△BEC
AE是△ABD的中线
∠DEC=∠AED
△DEC∽△AED
∠EDC=∠DAC
8. 如图,△ABC中,AB=AC,BD⊥AC于点D,求证:
A
B
C
D
证明:
法一
在AC上取点E,使得CD=ED连接BE.
∵CD=ED,BD⊥AC
∴BE=BC
∴∠BEC=∠BCE.
∵AB=AC. ∴∠ABC=∠ACB.
∴∠ABC=∠BEC.
又∵∠ACB=∠BCE.
∴△ABC∽△BEC.
∴
即 ,
E
思维拓展,更上一层
8. 如图,△ABC中,AB=AC,BD⊥AC于点D,求证:
A
B
C
D
E
法二
延长CA到点E,使得CA=AE,连接BE
AB=AC
AB=AC=CE
∠EBA=∠E,∠ABC=∠C
∠EBC=90°
BD⊥AC
△CDB∽△CBE
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
