浙教版九上数学每日一题16-20 二次函数与相似(含解析)
文档属性
| 名称 | 浙教版九上数学每日一题16-20 二次函数与相似(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 11:07:19 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
每日一题16 二次函数与相似
班级 姓名
16.如图,抛物线y=ax2+bx+2与x轴交于A,B两点,且OA=2OB,与y轴交于点C,连接BC,抛物线对称轴为直线x=,D为第一象限内抛物线上一动点,过点D作DE⊥OA于点E,与AC交于点F,设点D的横坐标为m.
(1)求抛物线的表达式;
(2)当线段DF的长度最大时,求D点的坐标;
(3)抛物线上是否存在点D,使得以点O,D,E为顶点的三角形与△BOC相似?若存在,求出m的值;若不存在,请说明理由.
每日一题17 二次函数与相似
班级 姓名
17.如图,抛物线与x轴交于点和点,与y轴交于点C,顶点为D,连接与抛物线的对称轴l交于点E.
(1)求抛物线的表达式;
(2)点P是第一象限内抛物线上的动点,连接,当时,求点P的坐标;
(3)点N是对称轴l右侧抛物线上的动点,在射线上是否存在点M,使得以点M,N,E为顶点的三角形与△相似?若存在,求点M的坐标;若不存在,请说明理由.
每日一题18 二次函数与相似
班级 姓名
18.如图,在平面直角坐标系中,矩形ABCD的边BC与x轴,y轴的交点分别为C(8,0),B(0,6),CD=5,抛物线y=ax2-x+c(a≠0)过B,C两点,动点M从点D开始以每秒5个单位长度的速度沿D-A-B-C的方向运动,到达C点后停止运动,动点N从点O以每秒4个单位长度的速度沿OC方向运动,到达C点后,立即返回,向CO方向运动,到达O点后又立即返回,依此在线段OC上反复运动,当点M停止时,点N也停止运动,设运动时间为t.
(1)求抛物线的解析式;
(2)求点D的坐标;
(3)当点M,N同时开始运动时,若以点M,D,C为顶点的三角形与以点B,O,N为顶点的三角形相似,求t的值;
(4)过点D与x轴平行的直线,交抛物线的对称轴于点Q,将线段BA沿过点B的直线翻折,点A的对称点为A′,求A′Q+QN+DN的最小值.
每日一题19 二次函数与相似
班级 姓名
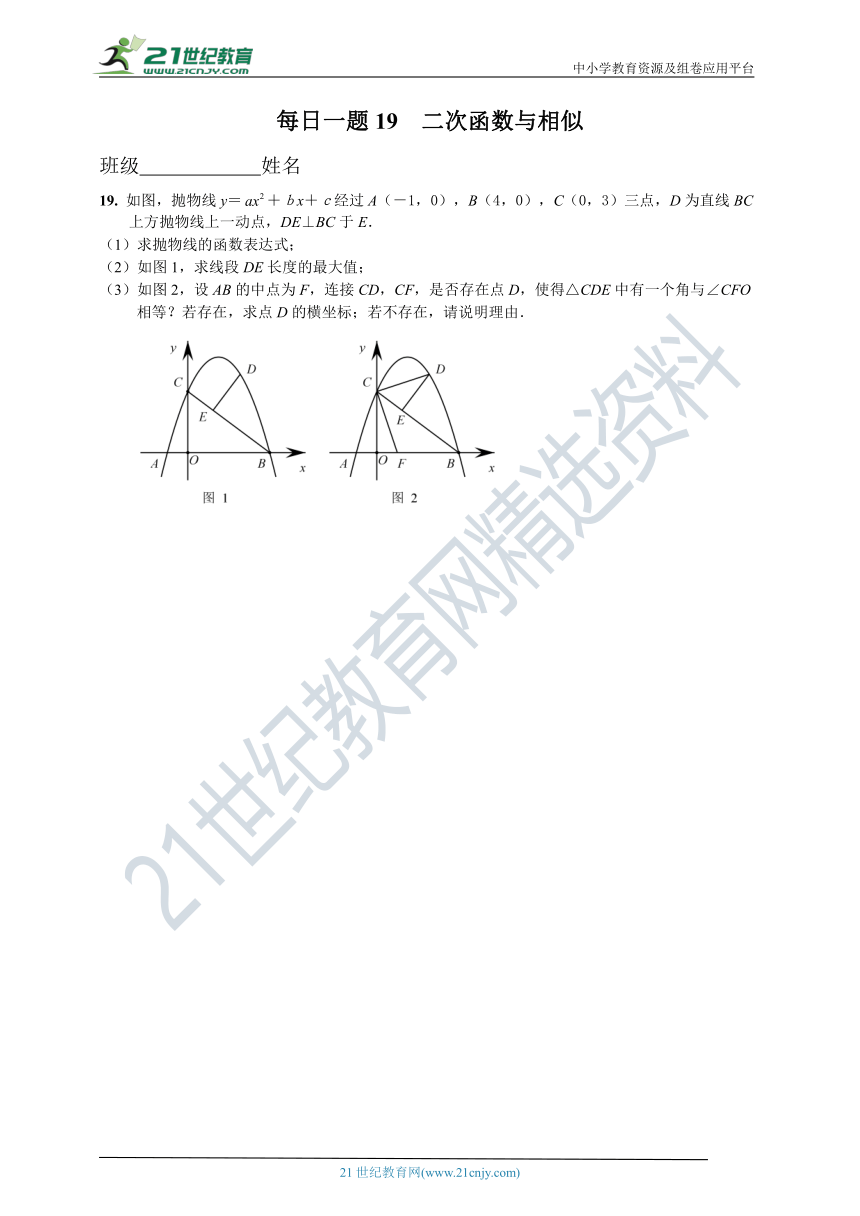
19. 如图,抛物线y=+bx+c经过A(-1,0),B(4,0),C(0,3)三点,D为直线BC上方抛物线上一动点,DE⊥BC于E.
(1)求抛物线的函数表达式;
(2)如图1,求线段DE长度的最大值;
(3)如图2,设AB的中点为F,连接CD,CF,是否存在点D,使得△CDE中有一个角与∠CFO相等?若存在,求点D的横坐标;若不存在,请说明理由.
每日一题20 二次函数与相似
班级 姓名
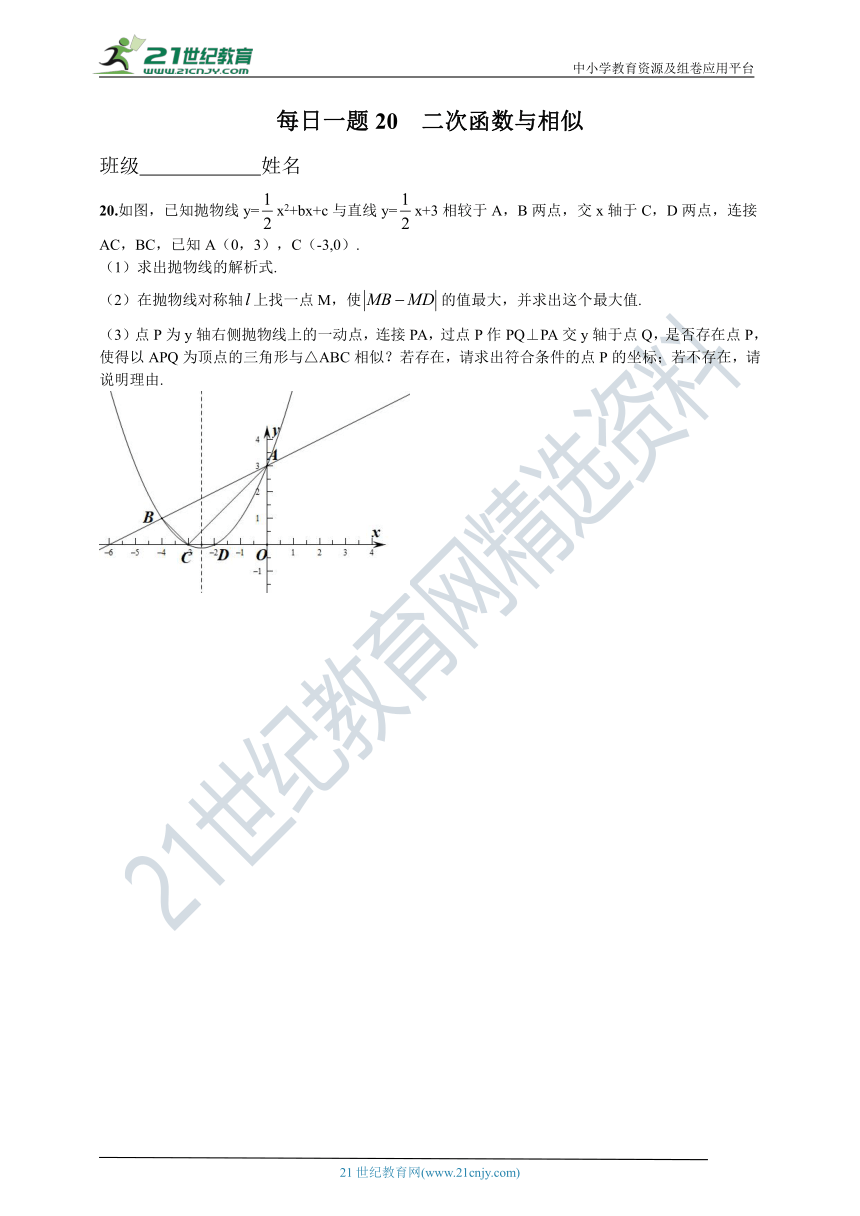
20.如图,已知抛物线y=x2+bx+c与直线y=x+3相较于A,B两点,交x轴于C,D两点,连接AC,BC,已知A(0,3),C(-3,0).
(1)求出抛物线的解析式.
(2)在抛物线对称轴上找一点M,使的值最大,并求出这个最大值.
(3)点P为y轴右侧抛物线上的一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,是否存在点P,使得以APQ为顶点的三角形与△ABC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
每日一题16 答案
16. 解:(1)设OB=t,则OA=2t,则点A、B的坐标分别为(2t,0)、(﹣t,0),
则x,解得:t=1,故点A、B的坐标分别为(2,0)、(﹣1,0),
则抛物线的表达式为:y=a(x﹣2)(x+1)=ax2+bx+2,解得:a=﹣1,
故抛物线的表达式为:y=﹣x2+x+2;
(2)对于y=﹣x2+x+2,令x=0,则y=2,故点C(0,2),
由点A、C的坐标得,直线AC的表达式为:y=﹣x+2,
设点D的横坐标为m,则点D(m,﹣m2+m+2),则点F(m,﹣m+2),
则DF=﹣m2+m+2﹣(﹣m+2)=﹣m2+2m,
∵﹣1<0,故DF有最大值,此时m=1,点D(1,2);
(3)存在,理由:
点D(m,﹣m2+m+2)(m>0),则OD=m,DE=﹣m2+m+2,
以点O,D,E为顶点的三角形与△BOC相似,
则,即2或,
解得:m=1或﹣2(舍去)或或(舍去),
故m=1或.
每日一题17 答案
17.(1)抛物线过点和点
∴,∴∴抛物线解析式为:.
(2)当时,,∴,∴直线BC解析式为:.
∵,∴.
过点P作PG轴,交轴于点G,交BC于点F
设,∴,∴,∴,即,∴,∴.
(3)∵,∴△为等腰直角三角形.
∵抛物线的对称轴为直线,
∴点E的横坐标为3.又点E在直线BC上,∴点E的纵坐标为5,∴.
设
①当MN=EM,,△NME∽△COB时
解得或(舍去)此时点M的坐标为
②当ME=EN,时
解得:或(舍去)此时点M的坐标为
③当MN=EN,时
连接CM,易知当N为C关于对称轴l的对称点时,△MNE∽△COB,此时四边形CMNE为正方形
解得:(舍去)此时点M的坐标为
在射线上存在点M,使得以点M,N,E为顶点的三角形与△相似,点M的坐标为:,或.
每日一题18 答案
18.解:(1)将代入得
,解得 ∴抛物线的解析式为:
(2)作于点E
∵ ∴ ∴
∵ ∴ ∴
∴ ∴ ∴
(3)若点M在DA上运动时,
当,则,即不成立,舍去
当,则,即,解得:,
若点M在BC上运动时,,
当,则,即,∴,
当时,,∴,解得(舍去),
当时,,∴,无解;
当,则,即,∴,
当时,,
∴,解得(舍去),
当时,,
∴,解得,
综上所示:当时,;时;
(4)作点D关于x轴的对称点F,连接QF交x轴于点N
∵点D,∴点 由得对称轴为 ∴点
∴
∴
故最小值为.
每日一题19 答案
解:(1)由题意得,,解得,. ∴y=+3.
(2)设直线BC的解析式为y=kx+b,
∴,解得,∴y=﹣x+3.
设D(a,+3)(0<a<4).过点D作DM⊥x轴交BC于M.∴M(a,﹣a+3).
∴DM==.
∵∠DME=∠OCB,∠DEM=∠COB,∴△DEM∽△BOC,∴=.
∵OB=4,OC=3,∴BC=5,∴DE=DM.
∴DE==.当a=2时,DE取最大值,最大值是.
(3)假设存在这样的点D,使得△CDE中有一个角与∠CFO相等.
∵F是AB的中点,∴OF=,tan∠CFO==2.
过点B作BG⊥BC交CD的延长线于G,过点G作GH⊥x轴,垂足为H.
∵DE⊥BC,故∠CED=90°,则只存在另外两个角与∠CFO相等.
①若∠DCE=∠CFO,∴tan∠DCE==2,∴BG=10.
∵△GBH∽△BCO,∴==.
∴GH=8,BH=6.∴G(10,8).
设直线CG的解析式为y=kx+b,∴,解得,∴y=x+3.
依题意得,,解得x=,或x=0(舍).
②若∠CDE=∠CFO,同理可得,BG=,GH=2,BH=,∴G(,2).
同理可得,直线CG的解析式为y=-x+3.
依题意得,,解得x=,或x=0(舍).
综上所述,存在D使得△CDE中有一个角与∠CFO相等,其横坐标为或.
每日一题20 答案
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
每日一题16 二次函数与相似
班级 姓名
16.如图,抛物线y=ax2+bx+2与x轴交于A,B两点,且OA=2OB,与y轴交于点C,连接BC,抛物线对称轴为直线x=,D为第一象限内抛物线上一动点,过点D作DE⊥OA于点E,与AC交于点F,设点D的横坐标为m.
(1)求抛物线的表达式;
(2)当线段DF的长度最大时,求D点的坐标;
(3)抛物线上是否存在点D,使得以点O,D,E为顶点的三角形与△BOC相似?若存在,求出m的值;若不存在,请说明理由.
每日一题17 二次函数与相似
班级 姓名
17.如图,抛物线与x轴交于点和点,与y轴交于点C,顶点为D,连接与抛物线的对称轴l交于点E.
(1)求抛物线的表达式;
(2)点P是第一象限内抛物线上的动点,连接,当时,求点P的坐标;
(3)点N是对称轴l右侧抛物线上的动点,在射线上是否存在点M,使得以点M,N,E为顶点的三角形与△相似?若存在,求点M的坐标;若不存在,请说明理由.
每日一题18 二次函数与相似
班级 姓名
18.如图,在平面直角坐标系中,矩形ABCD的边BC与x轴,y轴的交点分别为C(8,0),B(0,6),CD=5,抛物线y=ax2-x+c(a≠0)过B,C两点,动点M从点D开始以每秒5个单位长度的速度沿D-A-B-C的方向运动,到达C点后停止运动,动点N从点O以每秒4个单位长度的速度沿OC方向运动,到达C点后,立即返回,向CO方向运动,到达O点后又立即返回,依此在线段OC上反复运动,当点M停止时,点N也停止运动,设运动时间为t.
(1)求抛物线的解析式;
(2)求点D的坐标;
(3)当点M,N同时开始运动时,若以点M,D,C为顶点的三角形与以点B,O,N为顶点的三角形相似,求t的值;
(4)过点D与x轴平行的直线,交抛物线的对称轴于点Q,将线段BA沿过点B的直线翻折,点A的对称点为A′,求A′Q+QN+DN的最小值.
每日一题19 二次函数与相似
班级 姓名
19. 如图,抛物线y=+bx+c经过A(-1,0),B(4,0),C(0,3)三点,D为直线BC上方抛物线上一动点,DE⊥BC于E.
(1)求抛物线的函数表达式;
(2)如图1,求线段DE长度的最大值;
(3)如图2,设AB的中点为F,连接CD,CF,是否存在点D,使得△CDE中有一个角与∠CFO相等?若存在,求点D的横坐标;若不存在,请说明理由.
每日一题20 二次函数与相似
班级 姓名
20.如图,已知抛物线y=x2+bx+c与直线y=x+3相较于A,B两点,交x轴于C,D两点,连接AC,BC,已知A(0,3),C(-3,0).
(1)求出抛物线的解析式.
(2)在抛物线对称轴上找一点M,使的值最大,并求出这个最大值.
(3)点P为y轴右侧抛物线上的一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,是否存在点P,使得以APQ为顶点的三角形与△ABC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
每日一题16 答案
16. 解:(1)设OB=t,则OA=2t,则点A、B的坐标分别为(2t,0)、(﹣t,0),
则x,解得:t=1,故点A、B的坐标分别为(2,0)、(﹣1,0),
则抛物线的表达式为:y=a(x﹣2)(x+1)=ax2+bx+2,解得:a=﹣1,
故抛物线的表达式为:y=﹣x2+x+2;
(2)对于y=﹣x2+x+2,令x=0,则y=2,故点C(0,2),
由点A、C的坐标得,直线AC的表达式为:y=﹣x+2,
设点D的横坐标为m,则点D(m,﹣m2+m+2),则点F(m,﹣m+2),
则DF=﹣m2+m+2﹣(﹣m+2)=﹣m2+2m,
∵﹣1<0,故DF有最大值,此时m=1,点D(1,2);
(3)存在,理由:
点D(m,﹣m2+m+2)(m>0),则OD=m,DE=﹣m2+m+2,
以点O,D,E为顶点的三角形与△BOC相似,
则,即2或,
解得:m=1或﹣2(舍去)或或(舍去),
故m=1或.
每日一题17 答案
17.(1)抛物线过点和点
∴,∴∴抛物线解析式为:.
(2)当时,,∴,∴直线BC解析式为:.
∵,∴.
过点P作PG轴,交轴于点G,交BC于点F
设,∴,∴,∴,即,∴,∴.
(3)∵,∴△为等腰直角三角形.
∵抛物线的对称轴为直线,
∴点E的横坐标为3.又点E在直线BC上,∴点E的纵坐标为5,∴.
设
①当MN=EM,,△NME∽△COB时
解得或(舍去)此时点M的坐标为
②当ME=EN,时
解得:或(舍去)此时点M的坐标为
③当MN=EN,时
连接CM,易知当N为C关于对称轴l的对称点时,△MNE∽△COB,此时四边形CMNE为正方形
解得:(舍去)此时点M的坐标为
在射线上存在点M,使得以点M,N,E为顶点的三角形与△相似,点M的坐标为:,或.
每日一题18 答案
18.解:(1)将代入得
,解得 ∴抛物线的解析式为:
(2)作于点E
∵ ∴ ∴
∵ ∴ ∴
∴ ∴ ∴
(3)若点M在DA上运动时,
当,则,即不成立,舍去
当,则,即,解得:,
若点M在BC上运动时,,
当,则,即,∴,
当时,,∴,解得(舍去),
当时,,∴,无解;
当,则,即,∴,
当时,,
∴,解得(舍去),
当时,,
∴,解得,
综上所示:当时,;时;
(4)作点D关于x轴的对称点F,连接QF交x轴于点N
∵点D,∴点 由得对称轴为 ∴点
∴
∴
故最小值为.
每日一题19 答案
解:(1)由题意得,,解得,. ∴y=+3.
(2)设直线BC的解析式为y=kx+b,
∴,解得,∴y=﹣x+3.
设D(a,+3)(0<a<4).过点D作DM⊥x轴交BC于M.∴M(a,﹣a+3).
∴DM==.
∵∠DME=∠OCB,∠DEM=∠COB,∴△DEM∽△BOC,∴=.
∵OB=4,OC=3,∴BC=5,∴DE=DM.
∴DE==.当a=2时,DE取最大值,最大值是.
(3)假设存在这样的点D,使得△CDE中有一个角与∠CFO相等.
∵F是AB的中点,∴OF=,tan∠CFO==2.
过点B作BG⊥BC交CD的延长线于G,过点G作GH⊥x轴,垂足为H.
∵DE⊥BC,故∠CED=90°,则只存在另外两个角与∠CFO相等.
①若∠DCE=∠CFO,∴tan∠DCE==2,∴BG=10.
∵△GBH∽△BCO,∴==.
∴GH=8,BH=6.∴G(10,8).
设直线CG的解析式为y=kx+b,∴,解得,∴y=x+3.
依题意得,,解得x=,或x=0(舍).
②若∠CDE=∠CFO,同理可得,BG=,GH=2,BH=,∴G(,2).
同理可得,直线CG的解析式为y=-x+3.
依题意得,,解得x=,或x=0(舍).
综上所述,存在D使得△CDE中有一个角与∠CFO相等,其横坐标为或.
每日一题20 答案
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
