浙教版九上数学每日一题21-25 相似三角形综合应用(含解析)
文档属性
| 名称 | 浙教版九上数学每日一题21-25 相似三角形综合应用(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 11:08:24 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
每日一题21 相似三角形的综合应用
班级 小组 姓名
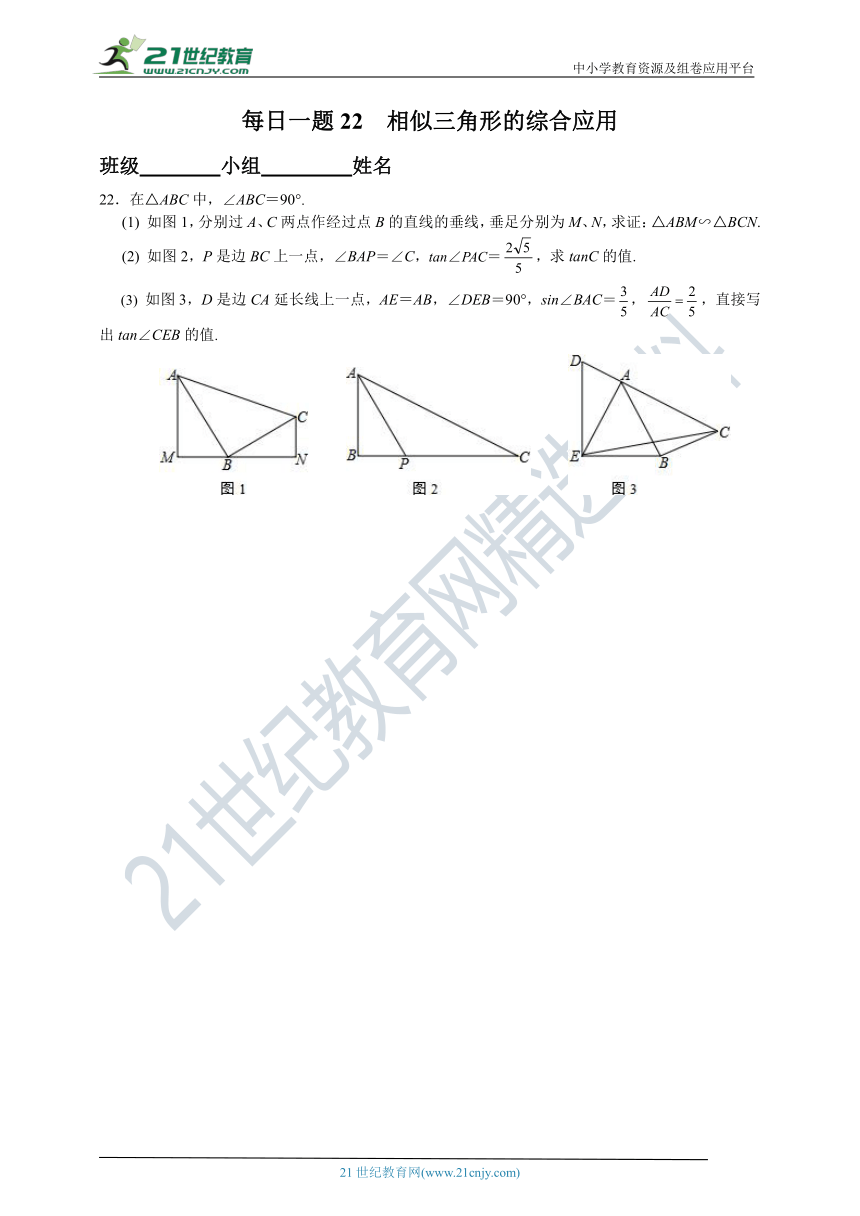
21.如图,在矩形纸片ABCD中,已知AB=1,BC=,点E在边CD上移动,连接AE,将多边形ABCF沿AE折叠,得到多边形AB’C’E,点B,C的对应点分别为点B’,C’,
(1)当B’C’恰好经过点D时(如图1)求线段CE的长;
(2)若B’C’分别交AD,CD于点F,G,且∠DAE=22.5°,(如图2),求△DFG的面积;
(3)在点E从点C移动到点D的过程中,求点C’移动的路径长.
每日一题22 相似三角形的综合应用
班级 小组 姓名
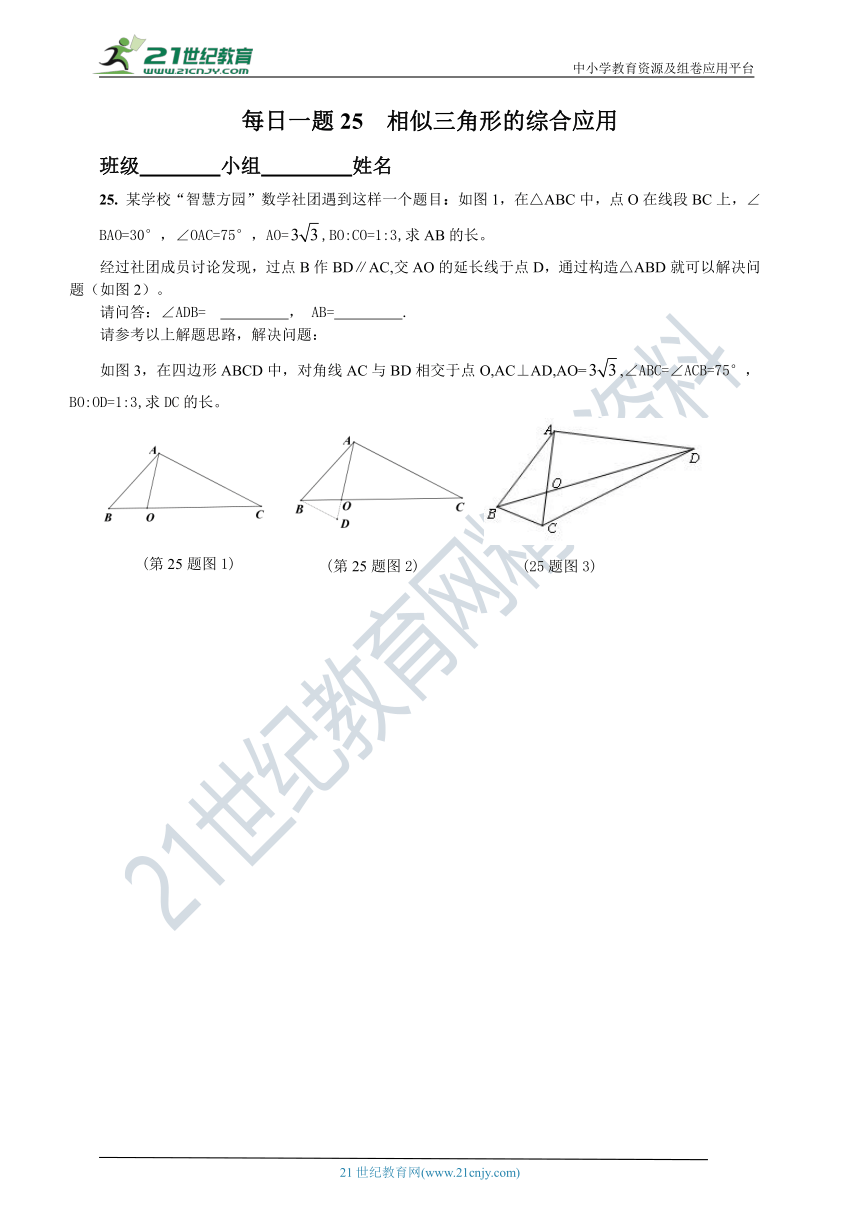
22.在△ABC中,∠ABC=90°.
(1) 如图1,分别过A、C两点作经过点B的直线的垂线,垂足分别为M、N,求证:△ABM∽△BCN.
(2) 如图2,P是边BC上一点,∠BAP=∠C,tan∠PAC=,求tanC的值.
(3) 如图3,D是边CA延长线上一点,AE=AB,∠DEB=90°,sin∠BAC=,,直接写出tan∠CEB的值.
每日一题23 相似三角形的综合应用
班级 小组 姓名
23.如图,在△ABC中,AB=4,∠B=45°,∠C=60°.
(1)求BC边上的高线长.
(2)点E为线段AB的中点,点F在边AC上,连结EF,沿EF将△AEF折叠得到△PEF.
①如图2,当点P落在BC上时,求∠AEP的度数.
②如图3,连结AP,当PF⊥AC时,求AP的长.
每日一题24 相似三角形的综合应用
班级 小组 姓名
24. 在数学兴趣小组活动中,小亮进行数学探究活动.△ABC是边长为2的等边三角形,E是AC上一点,小亮以BE为边向BE的右侧作等边三角形BEF,连接CF.
(1)如图1,当点E在线段AC上时,EF、BC相交于点D,小亮发现有两个三角形全等,请你找出来,并证明.
(2)当点E在线段AC上运动时,点F也随着运动,若四边形ABFC的面积为求AE的长.
(3)如图2,当点E在AC的延长线上运动时,CF、BE相交于点D,请你探求△ECD的面积S1与△DBF的面积S2之间的数量关系,并说明理由.
(4)如图2,当△ECD的面积S1=时,求AE的长.
图1 图2
每日一题25 相似三角形的综合应用
班级 小组 姓名
25. 某学校“智慧方园”数学社团遇到这样一个题目:如图1,在△ABC中,点O在线段BC上,∠BAO=30°,∠OAC=75°,AO=,BO:CO=1:3,求AB的长。
经过社团成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图2)。
请问答:∠ADB= , AB= .
请参考以上解题思路,解决问题:
如图3,在四边形ABCD中,对角线AC与BD相交于点O,AC⊥AD,AO=,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长。
每日一题21 答案
21.解:(1)由折叠知:∠B’=∠B=90°,AB’=AB=1,B’C’=BC=,C’E=CE;
由勾股定理得B’D==,∴D’C’=-,
∵∠ADE=90°,∴∠ADB’+∠EDC’=90°
∵∠ADB’+∠DAB’=90°,∴∠EDC’=∠DAB’,
∵∠B’=∠C’=90°,∴△AB’D∽△DC’E
∴,即,∴CE=;
(2)如图,连接AC,
∵tan∠BAC=,∴∠BAC=60°,∠DAC=60°,
∵∠DAE=22.5°,∴∠EAC=30°-22.5°=7.5°,
由折叠得∠B’AE=∠BAE=67.5°
∴∠B’AF=45°,∴AF=,DF=-,
∵∠B’FA=45°,∴S△DFG==;
(3)如图,连接AC’,则AC’=AC=2,
∴点C’的运动路径是以点A为圆心,以AC为半径的圆弧,
当点E运动到点D时,点C’恰好在CD的延长线上,此时∠CAC’=60°,
∴点C’移动的路径长是.
每日一题22 答案
【解题过程】证明:
⑴∵∠ABC=90°,
∴∠3+∠2=180°-∠ABC=180°-90°=90°,
又∵AM⊥MN,CN⊥MN,
∴∠M=∠N=90°,∠1+∠3=90°,
∴∠1=∠2. ∴△ABM∽△BCN. 37⑴答题图
(2)过P点作PN⊥AP交AC于N点,过N作NM⊥BC于M点,
∵∠BAP+∠APB=90°,∠APB+∠NPC=90°,
∴∠BAP=∠NPC,△BAP∽△MPN,
,又∵,
设,,则,, 37(2)答题图
又∵,∴,∴,
又△∽△,,∴,
,解得:, ∴.
(3)过作交于,过作交的延长线于
∵ ∴,易知△∽△,
设,∵△∽△,∴,∴
∴,∴
37(3)答题图
每日一题23 答案
【解答】解:(1)如图1中,过点A作AD⊥BC于D.
在Rt△ABD中,AD=AB sin45°=4.
(2)①如图2中,
∵△AEF≌△PEF,∴AE=EP,∵AE=EB,∴BE=EP,∴∠EPB=∠B=45°,∴∠PEB=90°,∴∠AEP=180°﹣90°=90°.
②如图3中,由(1)可知:AC,
∵PF⊥AC,∴∠PFA=90°,∵△AEF≌△PEF,∴∠AFE=∠PFE=45°,
∴∠AFE=∠B,∵∠EAF=∠CAB,∴△AEF∽△ACB,
∴,即,∴AF=2,在Rt△AFP,AF=FP,
∴AP=AF=2.
每日一题24 答案
【解题过程】(1)发现点E沿边AC从点A向点C运动过程中,始终有△ABE≌△CBF.
由图1知,△ABC与△EBF都是等边三角形,所以AB=CB,BE=BF,
又∠CBF=∠ABE=60°-∠CBE,所以△ABE≌△CBF.
(2)由(1)知点E在运动过程中始终有△ABE≌△CBF,
∵S四边形BECF=S△BCF+S△BCE,
∴S四边形BECF=S△ABC,∵△ABC的边长为2,则S△ABC=,
所以四边形BECF的面积为,又四边形ABFC的面积是,
所以S△ABE=,在三角形ABE中,因∠A=60°,所以边AB上的高为 AEsin60°,
则△ABE=AB· AEsin60°=×2×AE=,则AE=.
(3)S2-S1=.
由图2知,△ABC与△EBF都是等边三角形,所以AB=CB,BE=BF,
又∠CBF=∠ABE=60°+∠CBE,所以△ABE≌△CBF,
∴S△ABE=S△CBF,∴S△FDB=S△ECD+S△ABC,
则S△FDB-S△ECD=S△ABC=,则S2-S1=.
(4)由(3)知S2-S1=,即S△FDB-S△ECD=,
由S△ECD=,得S△BDF=,因△ABE≌△CBF,
所以AE=CF,∠BAE=∠BCF=60°,
又∠BAE=∠ABC=60°,得∠ABC=∠BCF,所以CF∥AB,则△BDF的高是,
则DF=,设CE=x,则2+x=CD+DF=CD+,所以CD=x-,
在△ABE中,由CD∥AB得, ,即,
化简得3x2-x-2=0,所以x=1或x= (舍),
即CE=1,所以AE=3.
每日一题25 答案
【解题过程】
(1)∵BD∥AC ∴∠BDO=∠OAC=75°,
∵∠AOC=∠DOB ∴△DOB∽△AOC
∴ ∵AO= ∴DO=. ∴AD=AO+DO=+=.
∵在△ABD中,∠BAO=30°,∠ADB=75°,
∴∠ABD=180°-∠BAO-∠ADB=180°-30°-75°=75°,
∴∠ABD=∠ADB ∴AB=AD=.
(2)解:过点B作BE∥AD交AC于点E
∵AC⊥AD ∴∠DAC =∠BEA=90°
∵∠AOD =∠EOB ∴△AOD∽△EOB ∴
∵BO:OD=1:3 ∴.
∵AO= ∴EO= ∴AE=
∵∠ABC=∠ACB=75° ∴∠BAC=30°,AB=AC.
∴AB=2BE
在Rt△AEB中,
即,得BE=4.
∴AB=AC=8,AD=12.
在Rt△CAD中,
即,得CD=
(第25题图1)
(第25题图2)
(25题图3)
(第40题答案图)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
每日一题21 相似三角形的综合应用
班级 小组 姓名
21.如图,在矩形纸片ABCD中,已知AB=1,BC=,点E在边CD上移动,连接AE,将多边形ABCF沿AE折叠,得到多边形AB’C’E,点B,C的对应点分别为点B’,C’,
(1)当B’C’恰好经过点D时(如图1)求线段CE的长;
(2)若B’C’分别交AD,CD于点F,G,且∠DAE=22.5°,(如图2),求△DFG的面积;
(3)在点E从点C移动到点D的过程中,求点C’移动的路径长.
每日一题22 相似三角形的综合应用
班级 小组 姓名
22.在△ABC中,∠ABC=90°.
(1) 如图1,分别过A、C两点作经过点B的直线的垂线,垂足分别为M、N,求证:△ABM∽△BCN.
(2) 如图2,P是边BC上一点,∠BAP=∠C,tan∠PAC=,求tanC的值.
(3) 如图3,D是边CA延长线上一点,AE=AB,∠DEB=90°,sin∠BAC=,,直接写出tan∠CEB的值.
每日一题23 相似三角形的综合应用
班级 小组 姓名
23.如图,在△ABC中,AB=4,∠B=45°,∠C=60°.
(1)求BC边上的高线长.
(2)点E为线段AB的中点,点F在边AC上,连结EF,沿EF将△AEF折叠得到△PEF.
①如图2,当点P落在BC上时,求∠AEP的度数.
②如图3,连结AP,当PF⊥AC时,求AP的长.
每日一题24 相似三角形的综合应用
班级 小组 姓名
24. 在数学兴趣小组活动中,小亮进行数学探究活动.△ABC是边长为2的等边三角形,E是AC上一点,小亮以BE为边向BE的右侧作等边三角形BEF,连接CF.
(1)如图1,当点E在线段AC上时,EF、BC相交于点D,小亮发现有两个三角形全等,请你找出来,并证明.
(2)当点E在线段AC上运动时,点F也随着运动,若四边形ABFC的面积为求AE的长.
(3)如图2,当点E在AC的延长线上运动时,CF、BE相交于点D,请你探求△ECD的面积S1与△DBF的面积S2之间的数量关系,并说明理由.
(4)如图2,当△ECD的面积S1=时,求AE的长.
图1 图2
每日一题25 相似三角形的综合应用
班级 小组 姓名
25. 某学校“智慧方园”数学社团遇到这样一个题目:如图1,在△ABC中,点O在线段BC上,∠BAO=30°,∠OAC=75°,AO=,BO:CO=1:3,求AB的长。
经过社团成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图2)。
请问答:∠ADB= , AB= .
请参考以上解题思路,解决问题:
如图3,在四边形ABCD中,对角线AC与BD相交于点O,AC⊥AD,AO=,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长。
每日一题21 答案
21.解:(1)由折叠知:∠B’=∠B=90°,AB’=AB=1,B’C’=BC=,C’E=CE;
由勾股定理得B’D==,∴D’C’=-,
∵∠ADE=90°,∴∠ADB’+∠EDC’=90°
∵∠ADB’+∠DAB’=90°,∴∠EDC’=∠DAB’,
∵∠B’=∠C’=90°,∴△AB’D∽△DC’E
∴,即,∴CE=;
(2)如图,连接AC,
∵tan∠BAC=,∴∠BAC=60°,∠DAC=60°,
∵∠DAE=22.5°,∴∠EAC=30°-22.5°=7.5°,
由折叠得∠B’AE=∠BAE=67.5°
∴∠B’AF=45°,∴AF=,DF=-,
∵∠B’FA=45°,∴S△DFG==;
(3)如图,连接AC’,则AC’=AC=2,
∴点C’的运动路径是以点A为圆心,以AC为半径的圆弧,
当点E运动到点D时,点C’恰好在CD的延长线上,此时∠CAC’=60°,
∴点C’移动的路径长是.
每日一题22 答案
【解题过程】证明:
⑴∵∠ABC=90°,
∴∠3+∠2=180°-∠ABC=180°-90°=90°,
又∵AM⊥MN,CN⊥MN,
∴∠M=∠N=90°,∠1+∠3=90°,
∴∠1=∠2. ∴△ABM∽△BCN. 37⑴答题图
(2)过P点作PN⊥AP交AC于N点,过N作NM⊥BC于M点,
∵∠BAP+∠APB=90°,∠APB+∠NPC=90°,
∴∠BAP=∠NPC,△BAP∽△MPN,
,又∵,
设,,则,, 37(2)答题图
又∵,∴,∴,
又△∽△,,∴,
,解得:, ∴.
(3)过作交于,过作交的延长线于
∵ ∴,易知△∽△,
设,∵△∽△,∴,∴
∴,∴
37(3)答题图
每日一题23 答案
【解答】解:(1)如图1中,过点A作AD⊥BC于D.
在Rt△ABD中,AD=AB sin45°=4.
(2)①如图2中,
∵△AEF≌△PEF,∴AE=EP,∵AE=EB,∴BE=EP,∴∠EPB=∠B=45°,∴∠PEB=90°,∴∠AEP=180°﹣90°=90°.
②如图3中,由(1)可知:AC,
∵PF⊥AC,∴∠PFA=90°,∵△AEF≌△PEF,∴∠AFE=∠PFE=45°,
∴∠AFE=∠B,∵∠EAF=∠CAB,∴△AEF∽△ACB,
∴,即,∴AF=2,在Rt△AFP,AF=FP,
∴AP=AF=2.
每日一题24 答案
【解题过程】(1)发现点E沿边AC从点A向点C运动过程中,始终有△ABE≌△CBF.
由图1知,△ABC与△EBF都是等边三角形,所以AB=CB,BE=BF,
又∠CBF=∠ABE=60°-∠CBE,所以△ABE≌△CBF.
(2)由(1)知点E在运动过程中始终有△ABE≌△CBF,
∵S四边形BECF=S△BCF+S△BCE,
∴S四边形BECF=S△ABC,∵△ABC的边长为2,则S△ABC=,
所以四边形BECF的面积为,又四边形ABFC的面积是,
所以S△ABE=,在三角形ABE中,因∠A=60°,所以边AB上的高为 AEsin60°,
则△ABE=AB· AEsin60°=×2×AE=,则AE=.
(3)S2-S1=.
由图2知,△ABC与△EBF都是等边三角形,所以AB=CB,BE=BF,
又∠CBF=∠ABE=60°+∠CBE,所以△ABE≌△CBF,
∴S△ABE=S△CBF,∴S△FDB=S△ECD+S△ABC,
则S△FDB-S△ECD=S△ABC=,则S2-S1=.
(4)由(3)知S2-S1=,即S△FDB-S△ECD=,
由S△ECD=,得S△BDF=,因△ABE≌△CBF,
所以AE=CF,∠BAE=∠BCF=60°,
又∠BAE=∠ABC=60°,得∠ABC=∠BCF,所以CF∥AB,则△BDF的高是,
则DF=,设CE=x,则2+x=CD+DF=CD+,所以CD=x-,
在△ABE中,由CD∥AB得, ,即,
化简得3x2-x-2=0,所以x=1或x= (舍),
即CE=1,所以AE=3.
每日一题25 答案
【解题过程】
(1)∵BD∥AC ∴∠BDO=∠OAC=75°,
∵∠AOC=∠DOB ∴△DOB∽△AOC
∴ ∵AO= ∴DO=. ∴AD=AO+DO=+=.
∵在△ABD中,∠BAO=30°,∠ADB=75°,
∴∠ABD=180°-∠BAO-∠ADB=180°-30°-75°=75°,
∴∠ABD=∠ADB ∴AB=AD=.
(2)解:过点B作BE∥AD交AC于点E
∵AC⊥AD ∴∠DAC =∠BEA=90°
∵∠AOD =∠EOB ∴△AOD∽△EOB ∴
∵BO:OD=1:3 ∴.
∵AO= ∴EO= ∴AE=
∵∠ABC=∠ACB=75° ∴∠BAC=30°,AB=AC.
∴AB=2BE
在Rt△AEB中,
即,得BE=4.
∴AB=AC=8,AD=12.
在Rt△CAD中,
即,得CD=
(第25题图1)
(第25题图2)
(25题图3)
(第40题答案图)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
