浙教版数学八年级上册 3.3.3一元一次不等式的应用 课件(共17张PPT)
文档属性
| 名称 | 浙教版数学八年级上册 3.3.3一元一次不等式的应用 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 626.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-26 09:19:01 | ||
图片预览






文档简介
(共17张PPT)
3.3 一元一次不等式
第3课时 一元一次不等式的应用
学习目标
1.能根据具体问题中的数量关系列一元一次不等式;
2.可以利用一元一次不等式解决简单实际问题.
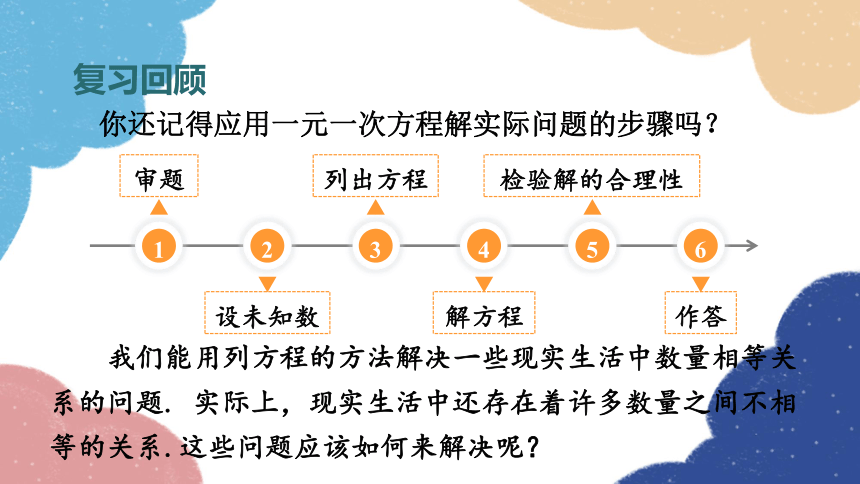
你还记得应用一元一次方程解实际问题的步骤吗?
1
2
3
4
5
6
审题
设未知数
列出方程
解方程
检验解的合理性
作答
我们能用列方程的方法解决一些现实生活中数量相等关系的问题. 实际上,现实生活中还存在着许多数量之间不相等的关系.这些问题应该如何来解决呢?
复习回顾
合作学习
一部电梯的额定限载量为1 000千克.两人要用电梯把一批重物从底层搬到顶层,这两人的身体质量分别为60千克和80千克,货物每箱的质量为50千克,问他们每次最多只能搬运重物多少箱?
讨论以下问题:
(1)选择哪一种数学模型?是列方程,还是列不等式?
(2)问题中有哪些相等的数量关系和不等的数量关系?
解决问题:
(1)列不等式.
(2)设每次搬x箱,相等关系有:
货物总质量=50x; 电梯内人与货物总质量=50x+60+80;
不等关系有:人与货物的总质量≤1 000.
列出不等式:50x+60+80≤1 000.
解得x≤17.2.
答:每次最多能搬17箱.
应用一元一次不等式可以刻画和解决很多实际生活中的有关数量不等关系的问题.
例题讲解
有一家庭工厂投资2万元购进一台机器,生产某种商品.这种商品每个的成本是3元,出售价是5元,应付的税款和其他费用是销售收入的10%. 问至少需要生产、销售多少个这种商品,才能使所获利润(毛利润减去税款和其他费用)超过投资购买机器的费用?
分析:每生产、销售一个这种商品的利润是(5-3-5×10%)元,
因此生产、销售x个这种商品的利润是(5-3-5×10%)x元.
问题中不等的数量关系是:所获利润>购买机器款.
根据解题过程,总结列不等式解决实际问题的方法步骤.
归纳总结
列不等式解应用题的基本步骤与列方程解应用题的
步骤类似,可概括为:“审、设、列、解、验、答”六步,
其不同点是方程是找相等关系,不等式是找不等关系.
随堂练习
1.某次知识竞赛共有20道题,每一题答对得10分,答错或不答都扣5分,小明得分想要超过120分,他至少要答对多少道题?如果设小明答对x道题,那么他答错或不答的题数为20-x,根据题意,得( )
A.10x-5(20-x)≥120 B.10x-5(20-x)≤120
C.10x-5(20-x)>120 D.10x-5(20-x)<120
C
2.现用甲、乙两种运输车将56 t救灾物资运往灾区,甲种车的载重量为6 t,乙种车的载重量为5 t,安排的车辆不超过10辆,则甲种运输车至少安排( )
A.4辆 B.5辆 C.6辆 D.7辆
解析:设甲种车安排x辆,根据题意可列出不等式:
6x+5(10-x) ≥56,解得x≥6.
∴甲种车辆至少要安排6辆.
C
3.某经销商销售一批电话手表,第一个月以550元/块的价格售出60块,第二个月起降价,以500元/块的价格将这批电话手表全部售出,销售总额超过了5.5万元.这批电话手表至少有( )
A.103块 B.104块 C.105块 D.106块
解析:设这批电话手表有x块,
550×60+(x-60)×500>55 000,解得x>104.
∴这批电话手表至少有105块.
C
4.某商场推出一种购物“金卡”,凭卡在该商场购物均可按商品标价的九折优惠,但办理购物“金卡”时每张要收费100元购卡费,设按标价累计购物金额为x元,当x_______时,办理购物“金卡”省钱.
解析:在办理购物“金卡”省钱时,
满足的关系式为:标价x>购卡费+标价×0.9.
即:x>100+0.9x,解得x>1 000.
>1 000
5.一水果店进了某种水果1吨,进价是7元/千克,售价定为10元/千克.销售了一半时,商家为了尽快售完,准备打折出售.如果要使总利润不低于2 000元,那么余下的水果至多可按原定价的几折出售?
利用一元一次不等式解决实际问题的步骤
1.审题,找出已知条件和所求问题,
以及题中的等量关系和不等关系;
2.设未知数,用含未知数的代数式表示相关量;
3.根据题目中的不等关系列出不等式;
4.解不等式,求出未知数的取值范围;
5.根据问题的实际情况,写出答案.
课堂小结
列一元一次不等式解应用题,要抓住题中的关键词如“大于”“小于”“不大于”“不小于”
“不超过”“超过”“最多”“最少”“至少”等,找出题中的不等关系,列出不等式.
感谢观看!
3.3 一元一次不等式
第3课时 一元一次不等式的应用
学习目标
1.能根据具体问题中的数量关系列一元一次不等式;
2.可以利用一元一次不等式解决简单实际问题.
你还记得应用一元一次方程解实际问题的步骤吗?
1
2
3
4
5
6
审题
设未知数
列出方程
解方程
检验解的合理性
作答
我们能用列方程的方法解决一些现实生活中数量相等关系的问题. 实际上,现实生活中还存在着许多数量之间不相等的关系.这些问题应该如何来解决呢?
复习回顾
合作学习
一部电梯的额定限载量为1 000千克.两人要用电梯把一批重物从底层搬到顶层,这两人的身体质量分别为60千克和80千克,货物每箱的质量为50千克,问他们每次最多只能搬运重物多少箱?
讨论以下问题:
(1)选择哪一种数学模型?是列方程,还是列不等式?
(2)问题中有哪些相等的数量关系和不等的数量关系?
解决问题:
(1)列不等式.
(2)设每次搬x箱,相等关系有:
货物总质量=50x; 电梯内人与货物总质量=50x+60+80;
不等关系有:人与货物的总质量≤1 000.
列出不等式:50x+60+80≤1 000.
解得x≤17.2.
答:每次最多能搬17箱.
应用一元一次不等式可以刻画和解决很多实际生活中的有关数量不等关系的问题.
例题讲解
有一家庭工厂投资2万元购进一台机器,生产某种商品.这种商品每个的成本是3元,出售价是5元,应付的税款和其他费用是销售收入的10%. 问至少需要生产、销售多少个这种商品,才能使所获利润(毛利润减去税款和其他费用)超过投资购买机器的费用?
分析:每生产、销售一个这种商品的利润是(5-3-5×10%)元,
因此生产、销售x个这种商品的利润是(5-3-5×10%)x元.
问题中不等的数量关系是:所获利润>购买机器款.
根据解题过程,总结列不等式解决实际问题的方法步骤.
归纳总结
列不等式解应用题的基本步骤与列方程解应用题的
步骤类似,可概括为:“审、设、列、解、验、答”六步,
其不同点是方程是找相等关系,不等式是找不等关系.
随堂练习
1.某次知识竞赛共有20道题,每一题答对得10分,答错或不答都扣5分,小明得分想要超过120分,他至少要答对多少道题?如果设小明答对x道题,那么他答错或不答的题数为20-x,根据题意,得( )
A.10x-5(20-x)≥120 B.10x-5(20-x)≤120
C.10x-5(20-x)>120 D.10x-5(20-x)<120
C
2.现用甲、乙两种运输车将56 t救灾物资运往灾区,甲种车的载重量为6 t,乙种车的载重量为5 t,安排的车辆不超过10辆,则甲种运输车至少安排( )
A.4辆 B.5辆 C.6辆 D.7辆
解析:设甲种车安排x辆,根据题意可列出不等式:
6x+5(10-x) ≥56,解得x≥6.
∴甲种车辆至少要安排6辆.
C
3.某经销商销售一批电话手表,第一个月以550元/块的价格售出60块,第二个月起降价,以500元/块的价格将这批电话手表全部售出,销售总额超过了5.5万元.这批电话手表至少有( )
A.103块 B.104块 C.105块 D.106块
解析:设这批电话手表有x块,
550×60+(x-60)×500>55 000,解得x>104.
∴这批电话手表至少有105块.
C
4.某商场推出一种购物“金卡”,凭卡在该商场购物均可按商品标价的九折优惠,但办理购物“金卡”时每张要收费100元购卡费,设按标价累计购物金额为x元,当x_______时,办理购物“金卡”省钱.
解析:在办理购物“金卡”省钱时,
满足的关系式为:标价x>购卡费+标价×0.9.
即:x>100+0.9x,解得x>1 000.
>1 000
5.一水果店进了某种水果1吨,进价是7元/千克,售价定为10元/千克.销售了一半时,商家为了尽快售完,准备打折出售.如果要使总利润不低于2 000元,那么余下的水果至多可按原定价的几折出售?
利用一元一次不等式解决实际问题的步骤
1.审题,找出已知条件和所求问题,
以及题中的等量关系和不等关系;
2.设未知数,用含未知数的代数式表示相关量;
3.根据题目中的不等关系列出不等式;
4.解不等式,求出未知数的取值范围;
5.根据问题的实际情况,写出答案.
课堂小结
列一元一次不等式解应用题,要抓住题中的关键词如“大于”“小于”“不大于”“不小于”
“不超过”“超过”“最多”“最少”“至少”等,找出题中的不等关系,列出不等式.
感谢观看!
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
