浙教版九上数学每日一题26-30 与圆有关的函数综合题(含解析)
文档属性
| 名称 | 浙教版九上数学每日一题26-30 与圆有关的函数综合题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 11:09:18 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
每日一题26 与圆有关的函数综合题
班级: 姓名:
26.如图,已知二次函数的图象与轴交于两点与轴交于点,⊙的半径为为⊙上一动点.
(1)点的坐标分别为( ),( );
(2)是否存在点,使得为直角三角形?若存在,求出点的坐标;若不存在,请说明理由;
(3)连接,若为的中点,连接,则的最大值= .
(备用图)
每日一题27 与圆有关的函数综合题
班级: 姓名:
27.如图所示,在平面直角坐标系中,⊙C经过坐标原点O,且与x轴,y轴分别相交于M(4,0),N(0,3)两点.已知抛物线开口向上,与⊙C交于N,H,P三点,P为抛物线的顶点,抛物线的对称轴经过点C且垂直x轴于点D.
(1)求线段CD的长及顶点P的坐标;
(2)求抛物线的函数表达式;
(3)设抛物线交x轴于A,B两点,在抛物线上是否存在点Q,使得S四边形OPMN=8S△QAB,且△QAB∽△OBN成立?若存在,请求出Q点的坐标;若不存在,请说明理由.
每日一题28 与圆有关的函数综合题
班级: 姓名:
28.如图,直线与轴交于点,与轴交于点,抛物线。经过两点,与轴的另一个交点为.
(1)求抛物线的解析式;
(2)点是第一象限抛物线上的点,连接交直线于点,设点的横坐标为,与的比值为,求与的函数关系式,并求出与的比值的最大值;
(3)点是抛物线对称轴上的一动点,连接.设外接圆的圆心为,当的值最大时,求点的坐标.
每日一题29 与圆有关的函数综合题
班级: 姓名:
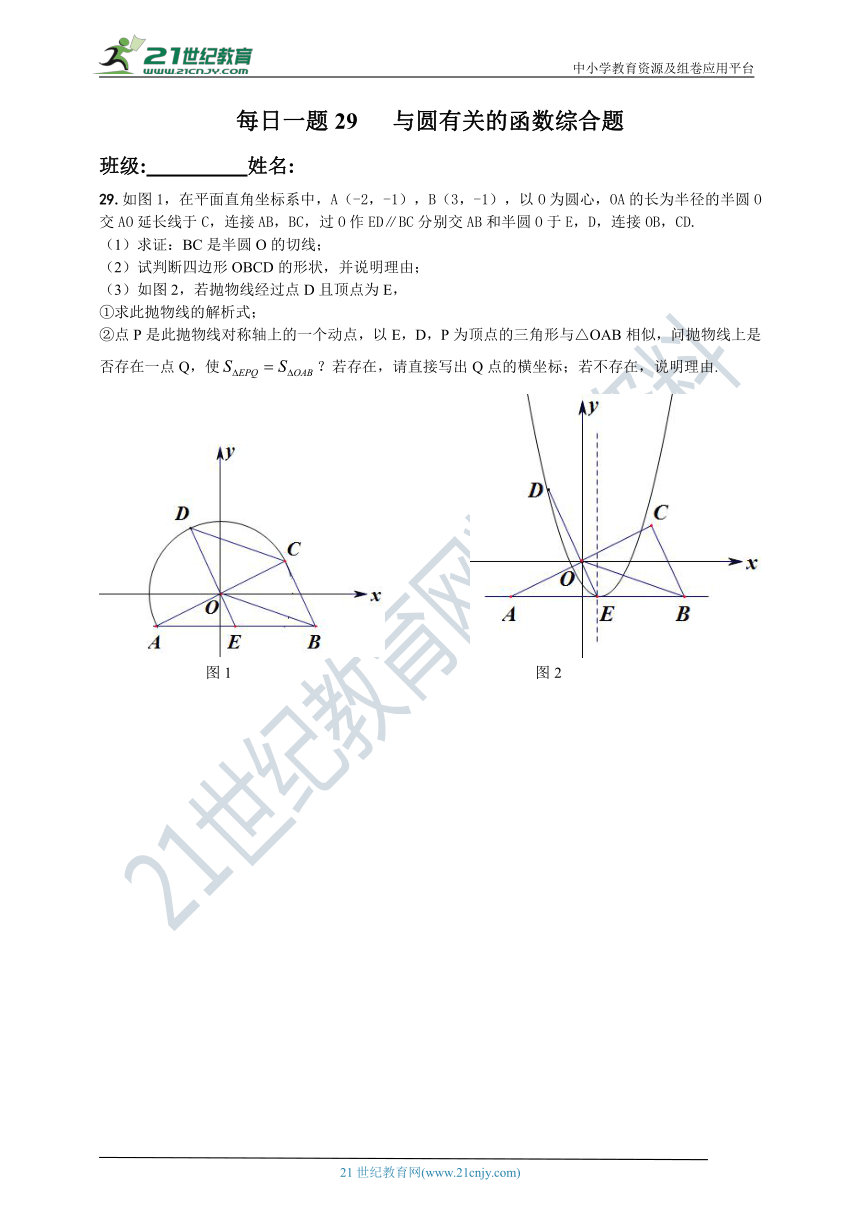
29.如图1,在平面直角坐标系中,A(-2,-1),B(3,-1),以O为圆心,OA的长为半径的半圆O交AO延长线于C,连接AB,BC,过O作ED∥BC分别交AB和半圆O于E,D,连接OB,CD.
(1)求证:BC是半圆O的切线;
(2)试判断四边形OBCD的形状,并说明理由;
(3)如图2,若抛物线经过点D且顶点为E,
①求此抛物线的解析式;
②点P是此抛物线对称轴上的一个动点,以E,D,P为顶点的三角形与△OAB相似,问抛物线上是否存在一点Q,使?若存在,请直接写出Q点的横坐标;若不存在,说明理由.
图1 图2
每日一题30 与圆有关的函数综合题
班级: 姓名:
30.已知如图,抛物线与x轴相交于B(1,0)、C(4,0)两点,与y轴的正半轴相交于A点,过A、B、C三点的⊙P与y轴相切于点A,M为y轴负半轴上的一个动点,直线MB交抛物线于N,交⊙P于D.
(1)填空:A点坐标是 ,⊙P半径的长是 ,a= ,b= ,c= ;
(2)若,求N点的坐标;
(3)若△AOB与以A、B、D为顶点的三角形相似,求MB MD的值.
每日一题26 答案
26.解:.(1)B(3,0),C(0,-4)
(2)设P(a,b)
若∠BPC=90°,则解得
∴P1(-1,-2)或P2(,-)
若∠BCP=90°,则解得
∴P3(,)或P4(,)
综上所述:符合条件的P共有4个:
P1(-1,-2)或P2(,-)或P3(,)或P4(,)
(3)
每日一题27 答案
27.解:(1)如图,连接OC,
∵M(4,0),N(0,3),∴OM=4,ON=3,
∴MN=5,∴OC=MN=,∵CD为抛物线对称轴,
∴OD=MD=2,
在Rt△OCD中,由勾股定理可得CD===,
∴PD=PC-CD==1,∴P(2,-1);
(2)∵抛物线的顶点为P(2,-1),
∴设抛物线的函数表达式为y=a(x-2)2-1,
∵抛物线过N(0,3),∴3=a(0-2)2-1,解得a=1,
∴抛物线的函数表达式为y=(x-2)2-1,即y=x2-4x+3;
(3)在y=x2-4x+3中,令y=0可得0=x2-4x+3,解得x=1或x=3,
∴A(1,0),B(3,0),∴AB=3-1=2,∵ON=3,OM=4,PD=1,
∴S四边形OPMN=S△OMP+S△OMN=OM PD+OM ON=×4×1+×4×3=8=8S△QAB,
∴S△QAB=1,设Q点纵坐标为y,则×2×|y|=1,解得y=1或y=-1,
当y=1时,则△QAB为钝角三角形,而△OBN为直角三角形,不合题意,舍去,
当y=-1时,可知P点即为所求的Q点,∵D为AB的中点,
∴AD=BD=QD,∴△QAB为等腰直角三角形,∵ON=OB=3,
∴△OBN为等腰直角三角形,∴△QAB∽△OBN,
综上可知存在满足条件的点Q,其坐标为(2,-1).
每日一题28 答案
28.【解题过程】解:(1)在y=-x+3种,令y=0得x=4,令x=0得y=3,
∴点A(4,0)、B(0,3),
把A(4,0)、B(0,3)代入y=-x2+bx+c,得:
,解得:,∴抛物线解析式为y=-x2+x+3;
(2)如图1,过点P作y轴的平行线交AB于点E,
则△PEQ∽△OBQ,∴,∵、OB=3, ∴y=PE,
∵P(m,-m2+m+3)、E(m,-m+3),则PE=(-m2+m+3)-(-m+3)=-m2+m,
∴y=(-m2+m)=-m2+m=-(m-2)2+,
∵0<m<3,∴当m=2时,y最大值=,∴PQ与OQ的比值的最大值为;
(3)由抛物线y=-x2+x+3易求C(-2,0),对称轴为直线x=1,
∵△ODC的外心为点M,∴点M在CO的垂直平分线上,
设CO的垂直平分线与CO交于点N,连接OM、CM、DM,
则∠ODC=∠CMO=∠OMN、MC=MO=MD,
∴sin∠ODC=sin∠OMN=,又MO=MD,
∴当MD取最小值时,sin∠ODC最大,此时⊙M与直线x=1相切,MD=2,
MN=,∴点M(-1,-),
根据对称性,另一点(-1,)也符合题意;
综上所述,点M的坐标为(-1,)或(-1,-).
每日一题29 答案
{答案} (1)证明: 如图,设AB与轴交于M,由题意,知:AM=2,OM=1,AB=5,则OA=OC=,
∵OE∥BC且O为AC的中点,∴OE为△ABC的中位线,∴,BC=2EO,
∴E(,-1),ME=,OM=1,∴,则,
在△ABC中,
∴△ABC为直角三角形且∠ACB=90°,即BC⊥AC,而AC为半圆O的直径,∴BC为半圆O的切线.
(2)四边形OBCD是平行四边形,理由:
如图1,由(1)中可得:BC=OD=OA=,
又∵OD∥BC,
∴四边形OBCD是平行四边形;
(3)①如图2,由(1)知: OD=OA=,E为AB中点且E(,-1),
过D作DN⊥轴于N,则DN∥ME,
∴△ODN∽△OEM,
∴,即,解得: ,,∴D点坐标为(-1,2).设此抛物线的解析式为,,则有:2= ,,解得:
∴此抛物线的解析式为,,即.
②存在符合题意的Q点,Q点的横坐标为或或或.
提示:由题意,易知: OA=,AB=5, D点坐标为(-1,2), E(,-1),M(0,-1)
∴DE=,tan∠OEP=,.
又∵A(-2,-1),tan∠A=,∴∠OEP=∠A,
当∠EDP′=∠AOB时,△AOB∽△EDP′,∴, 即,∴,
设此时Q点到对称轴的距离为,∵=,∴=,解得,∴点横坐标为: ,或点横坐标为:;
当∠EPD=∠AOB时,△AOB∽△EPD, ∴, 即,∴,
设此时Q点到对称轴的距离为,∵=,∴=,解得,∴点横坐标为: ,或点横坐标为:;
综上所述, Q点的横坐标为或或或.
每日一题30 答案
x
y
O
A
B
C
P
Q
A
B
C
x
y
O
备用图
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
每日一题26 与圆有关的函数综合题
班级: 姓名:
26.如图,已知二次函数的图象与轴交于两点与轴交于点,⊙的半径为为⊙上一动点.
(1)点的坐标分别为( ),( );
(2)是否存在点,使得为直角三角形?若存在,求出点的坐标;若不存在,请说明理由;
(3)连接,若为的中点,连接,则的最大值= .
(备用图)
每日一题27 与圆有关的函数综合题
班级: 姓名:
27.如图所示,在平面直角坐标系中,⊙C经过坐标原点O,且与x轴,y轴分别相交于M(4,0),N(0,3)两点.已知抛物线开口向上,与⊙C交于N,H,P三点,P为抛物线的顶点,抛物线的对称轴经过点C且垂直x轴于点D.
(1)求线段CD的长及顶点P的坐标;
(2)求抛物线的函数表达式;
(3)设抛物线交x轴于A,B两点,在抛物线上是否存在点Q,使得S四边形OPMN=8S△QAB,且△QAB∽△OBN成立?若存在,请求出Q点的坐标;若不存在,请说明理由.
每日一题28 与圆有关的函数综合题
班级: 姓名:
28.如图,直线与轴交于点,与轴交于点,抛物线。经过两点,与轴的另一个交点为.
(1)求抛物线的解析式;
(2)点是第一象限抛物线上的点,连接交直线于点,设点的横坐标为,与的比值为,求与的函数关系式,并求出与的比值的最大值;
(3)点是抛物线对称轴上的一动点,连接.设外接圆的圆心为,当的值最大时,求点的坐标.
每日一题29 与圆有关的函数综合题
班级: 姓名:
29.如图1,在平面直角坐标系中,A(-2,-1),B(3,-1),以O为圆心,OA的长为半径的半圆O交AO延长线于C,连接AB,BC,过O作ED∥BC分别交AB和半圆O于E,D,连接OB,CD.
(1)求证:BC是半圆O的切线;
(2)试判断四边形OBCD的形状,并说明理由;
(3)如图2,若抛物线经过点D且顶点为E,
①求此抛物线的解析式;
②点P是此抛物线对称轴上的一个动点,以E,D,P为顶点的三角形与△OAB相似,问抛物线上是否存在一点Q,使?若存在,请直接写出Q点的横坐标;若不存在,说明理由.
图1 图2
每日一题30 与圆有关的函数综合题
班级: 姓名:
30.已知如图,抛物线与x轴相交于B(1,0)、C(4,0)两点,与y轴的正半轴相交于A点,过A、B、C三点的⊙P与y轴相切于点A,M为y轴负半轴上的一个动点,直线MB交抛物线于N,交⊙P于D.
(1)填空:A点坐标是 ,⊙P半径的长是 ,a= ,b= ,c= ;
(2)若,求N点的坐标;
(3)若△AOB与以A、B、D为顶点的三角形相似,求MB MD的值.
每日一题26 答案
26.解:.(1)B(3,0),C(0,-4)
(2)设P(a,b)
若∠BPC=90°,则解得
∴P1(-1,-2)或P2(,-)
若∠BCP=90°,则解得
∴P3(,)或P4(,)
综上所述:符合条件的P共有4个:
P1(-1,-2)或P2(,-)或P3(,)或P4(,)
(3)
每日一题27 答案
27.解:(1)如图,连接OC,
∵M(4,0),N(0,3),∴OM=4,ON=3,
∴MN=5,∴OC=MN=,∵CD为抛物线对称轴,
∴OD=MD=2,
在Rt△OCD中,由勾股定理可得CD===,
∴PD=PC-CD==1,∴P(2,-1);
(2)∵抛物线的顶点为P(2,-1),
∴设抛物线的函数表达式为y=a(x-2)2-1,
∵抛物线过N(0,3),∴3=a(0-2)2-1,解得a=1,
∴抛物线的函数表达式为y=(x-2)2-1,即y=x2-4x+3;
(3)在y=x2-4x+3中,令y=0可得0=x2-4x+3,解得x=1或x=3,
∴A(1,0),B(3,0),∴AB=3-1=2,∵ON=3,OM=4,PD=1,
∴S四边形OPMN=S△OMP+S△OMN=OM PD+OM ON=×4×1+×4×3=8=8S△QAB,
∴S△QAB=1,设Q点纵坐标为y,则×2×|y|=1,解得y=1或y=-1,
当y=1时,则△QAB为钝角三角形,而△OBN为直角三角形,不合题意,舍去,
当y=-1时,可知P点即为所求的Q点,∵D为AB的中点,
∴AD=BD=QD,∴△QAB为等腰直角三角形,∵ON=OB=3,
∴△OBN为等腰直角三角形,∴△QAB∽△OBN,
综上可知存在满足条件的点Q,其坐标为(2,-1).
每日一题28 答案
28.【解题过程】解:(1)在y=-x+3种,令y=0得x=4,令x=0得y=3,
∴点A(4,0)、B(0,3),
把A(4,0)、B(0,3)代入y=-x2+bx+c,得:
,解得:,∴抛物线解析式为y=-x2+x+3;
(2)如图1,过点P作y轴的平行线交AB于点E,
则△PEQ∽△OBQ,∴,∵、OB=3, ∴y=PE,
∵P(m,-m2+m+3)、E(m,-m+3),则PE=(-m2+m+3)-(-m+3)=-m2+m,
∴y=(-m2+m)=-m2+m=-(m-2)2+,
∵0<m<3,∴当m=2时,y最大值=,∴PQ与OQ的比值的最大值为;
(3)由抛物线y=-x2+x+3易求C(-2,0),对称轴为直线x=1,
∵△ODC的外心为点M,∴点M在CO的垂直平分线上,
设CO的垂直平分线与CO交于点N,连接OM、CM、DM,
则∠ODC=∠CMO=∠OMN、MC=MO=MD,
∴sin∠ODC=sin∠OMN=,又MO=MD,
∴当MD取最小值时,sin∠ODC最大,此时⊙M与直线x=1相切,MD=2,
MN=,∴点M(-1,-),
根据对称性,另一点(-1,)也符合题意;
综上所述,点M的坐标为(-1,)或(-1,-).
每日一题29 答案
{答案} (1)证明: 如图,设AB与轴交于M,由题意,知:AM=2,OM=1,AB=5,则OA=OC=,
∵OE∥BC且O为AC的中点,∴OE为△ABC的中位线,∴,BC=2EO,
∴E(,-1),ME=,OM=1,∴,则,
在△ABC中,
∴△ABC为直角三角形且∠ACB=90°,即BC⊥AC,而AC为半圆O的直径,∴BC为半圆O的切线.
(2)四边形OBCD是平行四边形,理由:
如图1,由(1)中可得:BC=OD=OA=,
又∵OD∥BC,
∴四边形OBCD是平行四边形;
(3)①如图2,由(1)知: OD=OA=,E为AB中点且E(,-1),
过D作DN⊥轴于N,则DN∥ME,
∴△ODN∽△OEM,
∴,即,解得: ,,∴D点坐标为(-1,2).设此抛物线的解析式为,,则有:2= ,,解得:
∴此抛物线的解析式为,,即.
②存在符合题意的Q点,Q点的横坐标为或或或.
提示:由题意,易知: OA=,AB=5, D点坐标为(-1,2), E(,-1),M(0,-1)
∴DE=,tan∠OEP=,.
又∵A(-2,-1),tan∠A=,∴∠OEP=∠A,
当∠EDP′=∠AOB时,△AOB∽△EDP′,∴, 即,∴,
设此时Q点到对称轴的距离为,∵=,∴=,解得,∴点横坐标为: ,或点横坐标为:;
当∠EPD=∠AOB时,△AOB∽△EPD, ∴, 即,∴,
设此时Q点到对称轴的距离为,∵=,∴=,解得,∴点横坐标为: ,或点横坐标为:;
综上所述, Q点的横坐标为或或或.
每日一题30 答案
x
y
O
A
B
C
P
Q
A
B
C
x
y
O
备用图
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
