浙教版九上数学每日一题31-35 与圆有关的函数综合题(含解析)
文档属性
| 名称 | 浙教版九上数学每日一题31-35 与圆有关的函数综合题(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
每日一题31 与圆有关的函数综合题
班级: 姓名:
31.如图,已知的圆心为点,抛物线过点,与交于、两点,连接、,且,、两点的纵坐标分别是2、1.
(1)请直接写出点的坐标,并求、的值;
(2)直线经过点,与轴交于点.点(与点不重合)在该直线上,且,请判断点是否在此抛物线上,并说明理由;
(3)如果直线与相切,请直接写出满足此条件的直线解析式.
每日一题32 与圆有关的函数综合题
班级: 姓名:
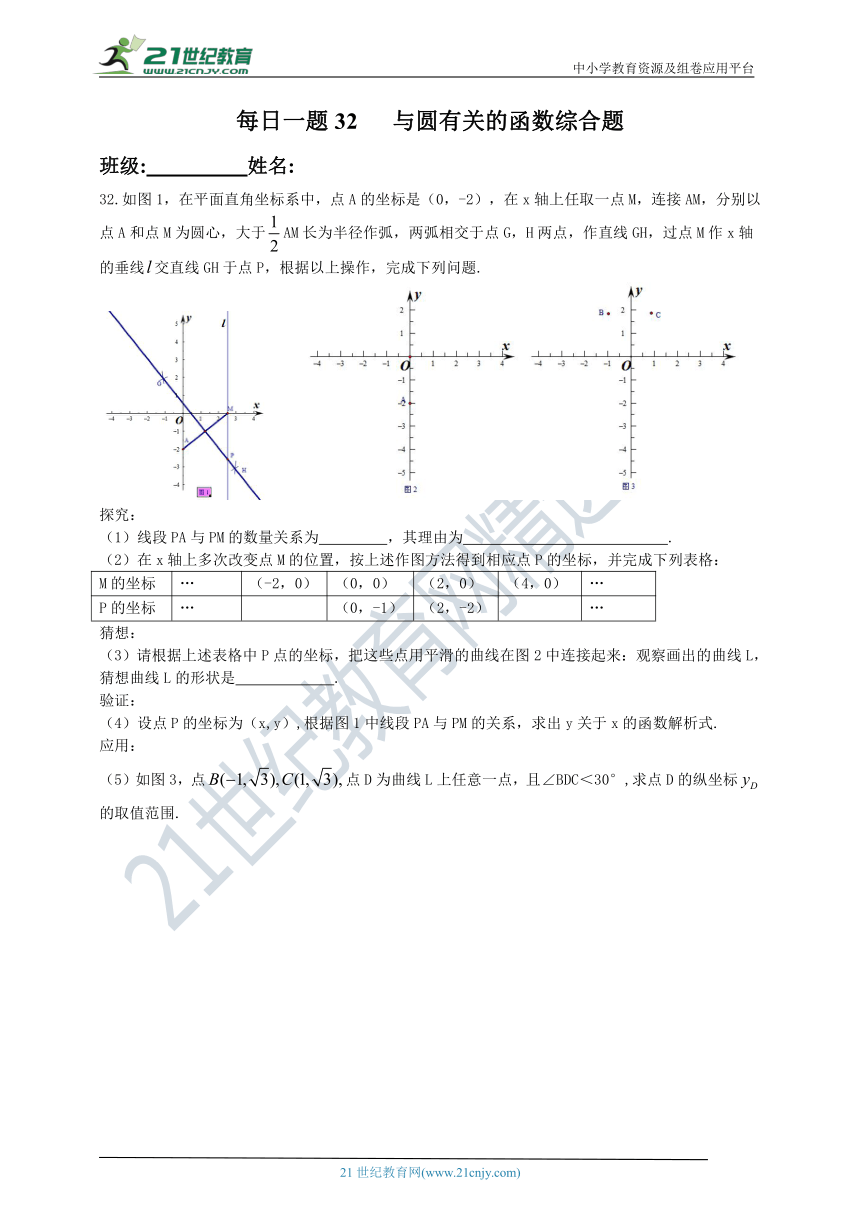
32.如图1,在平面直角坐标系中,点A的坐标是(0,-2),在x轴上任取一点M,连接AM,分别以点A和点M为圆心,大于AM长为半径作弧,两弧相交于点G,H两点,作直线GH,过点M作x轴的垂线交直线GH于点P,根据以上操作,完成下列问题.
探究:
(1)线段PA与PM的数量关系为 ,其理由为 .
(2)在x轴上多次改变点M的位置,按上述作图方法得到相应点P的坐标,并完成下列表格:
M的坐标 … (-2,0) (0,0) (2,0) (4,0) …
P的坐标 … (0,-1) (2,-2) …
猜想:
(3)请根据上述表格中P点的坐标,把这些点用平滑的曲线在图2中连接起来:观察画出的曲线L,猜想曲线L的形状是 .
验证:
(4)设点P的坐标为(x,y),根据图1中线段PA与PM的关系,求出y关于x的函数解析式.
应用:
(5)如图3,点点D为曲线L上任意一点,且∠BDC<30°,求点D的纵坐标的取值范围.
每日一题33 与圆有关的函数综合题
班级: 姓名:
33.如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点B,抛物线过点B且与直线相交于另一点.
(1)求抛物线的解析式;
(2)点P是抛物线上一动点,当时,求点P的坐标;
(3)点在x轴的正半轴上,点是y轴正半轴上的一动点,且满足.①求m与n之间的函数关系式;②当m在什么范围时,符合条件的N点的个数有2个?
每日一题34 与圆有关的函数综合题
班级: 姓名:
34.如图,顶点为M的抛物线与x轴交于,两点,与y轴交于点C,过点C作轴交抛物线与另一个点D,作轴,垂足为点E.双曲线经过点D,连接MD,BD.
(1)求抛物线的解析式.
(2)点N,F分别是x轴,y轴上的两点,当M,D,N,F为顶点的四边形周长最小时,求出点N,F的坐标;
(3)动点P从点O出发,以每秒1个单位长度的速度沿OC方向运动,运动时间为t秒,当t为何值时,的度数最大?(请直接写出结果)
备用图
每日一题35 与圆有关的函数综合题
班级: 姓名:
35.如图,在直角坐标系中,四边形OABC是平行四边形,经过A(﹣2,0),B,C三点的抛物线y=ax2+bx+(a<0)与x轴的另一个交点为D,其顶点为M,对称轴与x轴交于点E.
(1)求这条抛物线对应的函数表达式;
(2)已知R是抛物线上的点,使得△ADR的面积是 OABC的面积的,求点R的坐标;
(3)已知P是抛物线对称轴上的点,满足在直线MD上存在唯一的点Q,使得∠PQE=45°,求点P的坐标.
每日一题31 答案
解:(1)过点、分别作轴的垂线交于点、,
,,,又,
△,,,
故点、的坐标分别为、,
将点、坐标代入抛物线并解得:,,
故抛物线的表达式为:;
(2)将点坐标代入并解得:,则点,
点、、、的坐标分别为、、、,则,,
点在直线上,则设的坐标为,
,则,解得:或6(舍去,
故点,把代入,故点在抛物线上;
(3)①当切点在轴下方时,
设直线与相切于点,直线与轴、轴分别交于点、,连接,
,,
,,,
,即:,
解得:或(舍去,故点,
把点、坐标代入并解得:
直线的表达式为:;
②当切点在轴上方时,直线的表达式为:;
故满足条件的直线解析式为:或.
每日一题32 答案
{答案}解:(1)PA=PM,线段垂直平分线上的点与这条线段两个端点的距离相等.
(2)
M的坐标 … (-2,0) (0,0) (2,0) (4,0) …
P的坐标 … (-2,-2) (0,-1) (2,-2) (4,-5) …
(3)草图见图2,曲线L的形状是抛物线.
(4)如图1,过点P作PE⊥y轴于点E,
PA=PM=,AE=OE=OA=,PE=,
在Rt△PAE中,,即,
化简得,所以y关于x的解析式为.
(5)连接OB,OC,易得OB=OC=2,
∴△OBC是等边三角形,∴∠BOC=60°.
当∠BDC=30°时,在△BDC的外接圆上,弧BC所对的圆心角是60°.其圆心在BC的垂直平分线y轴上,
∴△BDC的外接圆圆心是坐标原点O.
设D(),则OD=2,即,①
又∵点D在抛物线上,∴.②
由①②联立解得:(舍去),
数形结合可得:当∠BDC<30°时,点D的纵坐标的取值范围为<.
每日一题33 答案
解:(1)∵直线与x轴交于点A,与y轴交于点B,令x=0,则y=2,令y=0,则x=4,∴A(4,0),B(0,2),∵抛物线经过B(0,2),,∴,解得:,
∴抛物线的表达式为:;
(2)当点P在x轴上方时,点P与点C重合,满足,∵,
∴,当点P在x轴下方时,如图,AP与y轴交于点Q,
∵,∴B,Q关于x轴对称,∴Q(0,-2),又A(4,0),
设直线AQ的表达式为y=px+q,代入,,解得:,
∴直线AQ的表达式为:,联立得:,解得:x=3或-2,
∴点P的坐标为(3,)或(-2,-3),
综上,当时,点P的坐标为:或(3,)或(-2,-3);
(3)①如图,∠MNC=90°,过点C作CD⊥x轴于点D,∴∠MNO+∠CND=90°,∵∠OMN+∠MNO=90°,∴∠CND=∠OMN,又∠MON=∠CDN=90°,∴△MNO∽△NCD,
∴,即,整理得:;
②如图,∵∠MNC=90°,以MC为直径画圆E,∵,
∴点N在线段OD上(不含O和D),即圆E与线段OD有两个交点(不含O和D),
∵点M在y轴正半轴,当圆E与线段OD相切时,有NE=MC,即NE2=MC2,
∵M(0,m),,∴E(,),∴=,
解得:m=,
当点M与点O重合时,如图,此时圆E与线段OD(不含O和D)有一个交点,
∴当0<m<时,圆E与线段OD有两个交点,故m的取值范围是:0<m<.
每日一题34 答案
(1)当时 所以,,
因为轴,轴,,所以四边形OEDC为矩形,
又因为双曲线经过点D, 所以,
所以,所以
将点、代入抛物线得
解得 所以抛物线的表达式为.
(2)解:作点D关于x轴的对称点,作点M关于y轴的对称点,如图(1)
由图形轴对称的性质可知,,所以四边形MDNF的周长,
因为是定值,所以当最小时,四边形MDNF的周长最小,
因为两点之间线段最短,所以当I、F、N、H在同一条直线上时最小
所以当I、F、N、H在同一条直线上时,四边形MDNF的周长最小,
连接,交x轴于点N,交y轴于点F,
因为抛物线的表达式为,所以点M的坐标为,
由轴对称的性质可得,,, 设直线HI的表达式为,
所以,解得,所以直线HI的表达式为,
当时,,当时,,所以,所以,,
所以当M,D,N,F为顶点的四边形周长最小时,,.
(3)解:本题的答案为.
解题分析:如图(2),当两点A、B距离是定值,直线CD是一条固定的直线,点P在直线CD上移动,由下图可以看出只有当过A、B的圆与直线CD相切时最大.
方法1:
方法2:
每日一题35 答案
解:(1)OA=2=BC,故函数的对称轴为x=1,则x=1①,
将点A的坐标代入抛物线表达式得:0=4a﹣2b+②,
联立①②并解得,故抛物线的表达式为:③;
(2)由抛物线的表达式得,点M(1,3)、点D(4,0);
∵△ADR的面积是 OABC的面积的,
∴AD×|yR|=OA×OB,则6×|yR|=2,解得:yR=±④,
联立④③并解得或,
故点R的坐标为(1+,4)或(1-,4)或(1+,﹣4)或(1-,﹣4);
(3)①先考虑特殊情况:
当Q与D重合时,P点坐标为(1,3)或(1,-3)刚好满足条件。
②Q在MD上且不与D重合:
方法2图
方法1图
第34题答图(2)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
每日一题31 与圆有关的函数综合题
班级: 姓名:
31.如图,已知的圆心为点,抛物线过点,与交于、两点,连接、,且,、两点的纵坐标分别是2、1.
(1)请直接写出点的坐标,并求、的值;
(2)直线经过点,与轴交于点.点(与点不重合)在该直线上,且,请判断点是否在此抛物线上,并说明理由;
(3)如果直线与相切,请直接写出满足此条件的直线解析式.
每日一题32 与圆有关的函数综合题
班级: 姓名:
32.如图1,在平面直角坐标系中,点A的坐标是(0,-2),在x轴上任取一点M,连接AM,分别以点A和点M为圆心,大于AM长为半径作弧,两弧相交于点G,H两点,作直线GH,过点M作x轴的垂线交直线GH于点P,根据以上操作,完成下列问题.
探究:
(1)线段PA与PM的数量关系为 ,其理由为 .
(2)在x轴上多次改变点M的位置,按上述作图方法得到相应点P的坐标,并完成下列表格:
M的坐标 … (-2,0) (0,0) (2,0) (4,0) …
P的坐标 … (0,-1) (2,-2) …
猜想:
(3)请根据上述表格中P点的坐标,把这些点用平滑的曲线在图2中连接起来:观察画出的曲线L,猜想曲线L的形状是 .
验证:
(4)设点P的坐标为(x,y),根据图1中线段PA与PM的关系,求出y关于x的函数解析式.
应用:
(5)如图3,点点D为曲线L上任意一点,且∠BDC<30°,求点D的纵坐标的取值范围.
每日一题33 与圆有关的函数综合题
班级: 姓名:
33.如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点B,抛物线过点B且与直线相交于另一点.
(1)求抛物线的解析式;
(2)点P是抛物线上一动点,当时,求点P的坐标;
(3)点在x轴的正半轴上,点是y轴正半轴上的一动点,且满足.①求m与n之间的函数关系式;②当m在什么范围时,符合条件的N点的个数有2个?
每日一题34 与圆有关的函数综合题
班级: 姓名:
34.如图,顶点为M的抛物线与x轴交于,两点,与y轴交于点C,过点C作轴交抛物线与另一个点D,作轴,垂足为点E.双曲线经过点D,连接MD,BD.
(1)求抛物线的解析式.
(2)点N,F分别是x轴,y轴上的两点,当M,D,N,F为顶点的四边形周长最小时,求出点N,F的坐标;
(3)动点P从点O出发,以每秒1个单位长度的速度沿OC方向运动,运动时间为t秒,当t为何值时,的度数最大?(请直接写出结果)
备用图
每日一题35 与圆有关的函数综合题
班级: 姓名:
35.如图,在直角坐标系中,四边形OABC是平行四边形,经过A(﹣2,0),B,C三点的抛物线y=ax2+bx+(a<0)与x轴的另一个交点为D,其顶点为M,对称轴与x轴交于点E.
(1)求这条抛物线对应的函数表达式;
(2)已知R是抛物线上的点,使得△ADR的面积是 OABC的面积的,求点R的坐标;
(3)已知P是抛物线对称轴上的点,满足在直线MD上存在唯一的点Q,使得∠PQE=45°,求点P的坐标.
每日一题31 答案
解:(1)过点、分别作轴的垂线交于点、,
,,,又,
△,,,
故点、的坐标分别为、,
将点、坐标代入抛物线并解得:,,
故抛物线的表达式为:;
(2)将点坐标代入并解得:,则点,
点、、、的坐标分别为、、、,则,,
点在直线上,则设的坐标为,
,则,解得:或6(舍去,
故点,把代入,故点在抛物线上;
(3)①当切点在轴下方时,
设直线与相切于点,直线与轴、轴分别交于点、,连接,
,,
,,,
,即:,
解得:或(舍去,故点,
把点、坐标代入并解得:
直线的表达式为:;
②当切点在轴上方时,直线的表达式为:;
故满足条件的直线解析式为:或.
每日一题32 答案
{答案}解:(1)PA=PM,线段垂直平分线上的点与这条线段两个端点的距离相等.
(2)
M的坐标 … (-2,0) (0,0) (2,0) (4,0) …
P的坐标 … (-2,-2) (0,-1) (2,-2) (4,-5) …
(3)草图见图2,曲线L的形状是抛物线.
(4)如图1,过点P作PE⊥y轴于点E,
PA=PM=,AE=OE=OA=,PE=,
在Rt△PAE中,,即,
化简得,所以y关于x的解析式为.
(5)连接OB,OC,易得OB=OC=2,
∴△OBC是等边三角形,∴∠BOC=60°.
当∠BDC=30°时,在△BDC的外接圆上,弧BC所对的圆心角是60°.其圆心在BC的垂直平分线y轴上,
∴△BDC的外接圆圆心是坐标原点O.
设D(),则OD=2,即,①
又∵点D在抛物线上,∴.②
由①②联立解得:(舍去),
数形结合可得:当∠BDC<30°时,点D的纵坐标的取值范围为<.
每日一题33 答案
解:(1)∵直线与x轴交于点A,与y轴交于点B,令x=0,则y=2,令y=0,则x=4,∴A(4,0),B(0,2),∵抛物线经过B(0,2),,∴,解得:,
∴抛物线的表达式为:;
(2)当点P在x轴上方时,点P与点C重合,满足,∵,
∴,当点P在x轴下方时,如图,AP与y轴交于点Q,
∵,∴B,Q关于x轴对称,∴Q(0,-2),又A(4,0),
设直线AQ的表达式为y=px+q,代入,,解得:,
∴直线AQ的表达式为:,联立得:,解得:x=3或-2,
∴点P的坐标为(3,)或(-2,-3),
综上,当时,点P的坐标为:或(3,)或(-2,-3);
(3)①如图,∠MNC=90°,过点C作CD⊥x轴于点D,∴∠MNO+∠CND=90°,∵∠OMN+∠MNO=90°,∴∠CND=∠OMN,又∠MON=∠CDN=90°,∴△MNO∽△NCD,
∴,即,整理得:;
②如图,∵∠MNC=90°,以MC为直径画圆E,∵,
∴点N在线段OD上(不含O和D),即圆E与线段OD有两个交点(不含O和D),
∵点M在y轴正半轴,当圆E与线段OD相切时,有NE=MC,即NE2=MC2,
∵M(0,m),,∴E(,),∴=,
解得:m=,
当点M与点O重合时,如图,此时圆E与线段OD(不含O和D)有一个交点,
∴当0<m<时,圆E与线段OD有两个交点,故m的取值范围是:0<m<.
每日一题34 答案
(1)当时 所以,,
因为轴,轴,,所以四边形OEDC为矩形,
又因为双曲线经过点D, 所以,
所以,所以
将点、代入抛物线得
解得 所以抛物线的表达式为.
(2)解:作点D关于x轴的对称点,作点M关于y轴的对称点,如图(1)
由图形轴对称的性质可知,,所以四边形MDNF的周长,
因为是定值,所以当最小时,四边形MDNF的周长最小,
因为两点之间线段最短,所以当I、F、N、H在同一条直线上时最小
所以当I、F、N、H在同一条直线上时,四边形MDNF的周长最小,
连接,交x轴于点N,交y轴于点F,
因为抛物线的表达式为,所以点M的坐标为,
由轴对称的性质可得,,, 设直线HI的表达式为,
所以,解得,所以直线HI的表达式为,
当时,,当时,,所以,所以,,
所以当M,D,N,F为顶点的四边形周长最小时,,.
(3)解:本题的答案为.
解题分析:如图(2),当两点A、B距离是定值,直线CD是一条固定的直线,点P在直线CD上移动,由下图可以看出只有当过A、B的圆与直线CD相切时最大.
方法1:
方法2:
每日一题35 答案
解:(1)OA=2=BC,故函数的对称轴为x=1,则x=1①,
将点A的坐标代入抛物线表达式得:0=4a﹣2b+②,
联立①②并解得,故抛物线的表达式为:③;
(2)由抛物线的表达式得,点M(1,3)、点D(4,0);
∵△ADR的面积是 OABC的面积的,
∴AD×|yR|=OA×OB,则6×|yR|=2,解得:yR=±④,
联立④③并解得或,
故点R的坐标为(1+,4)或(1-,4)或(1+,﹣4)或(1-,﹣4);
(3)①先考虑特殊情况:
当Q与D重合时,P点坐标为(1,3)或(1,-3)刚好满足条件。
②Q在MD上且不与D重合:
方法2图
方法1图
第34题答图(2)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
