浙教版九上数学每日一题36-40 与圆相关的新定义型问题(含解析)
文档属性
| 名称 | 浙教版九上数学每日一题36-40 与圆相关的新定义型问题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 11:12:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
每日一题36 与圆相关的新定义型问题
班级 小组 姓名
36.定义:三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角.
(1)如图1,∠E是△ABC中∠A的遥望角,若∠A=a,请用含a的代数式表示∠E.
(2)如图2,四边形ABCD内接于⊙O,=,四边形ABCD的外角平分线DF交⊙O于点F,连结BF并延长交CD的延长线于点E.求证:∠BEC是△ABC中∠BAC的遥望角.
(3)如图3,在(2)的条件下,连结AE,AF,若AC是⊙O的直径.
①求∠AED的度数;
②若AB=8,CD=5,求△DEF的面积.
每日一题37 与圆相关的新定义型问题
班级 小组 姓名
37.在平面直角坐标系xOy中,⊙O的半径为1,A,B为⊙O外两点,AB=1.给出如下定义:平移线段AB,得到⊙O的弦A B (A ,B 分别为点A,B的对应点),线段AA 长度的最小值称为线段AB到⊙O的“平移距离”.
(1)如图,平移线段AB到⊙O的长度为1的弦和,则这两条弦的位置关系是 ;在点中,连接点A与点 的线段的长度等于线段AB到⊙O的“平移距离”;
(2)若点A,B都在直线上,记线段AB到⊙O的“平移距离”为,求的最小值;
(3)若点A的坐标为,记线段AB到⊙O的“平移距离”为,直接写出的取值范围.
每日一题38 与圆相关的新定义型问题
班级 小组 姓名
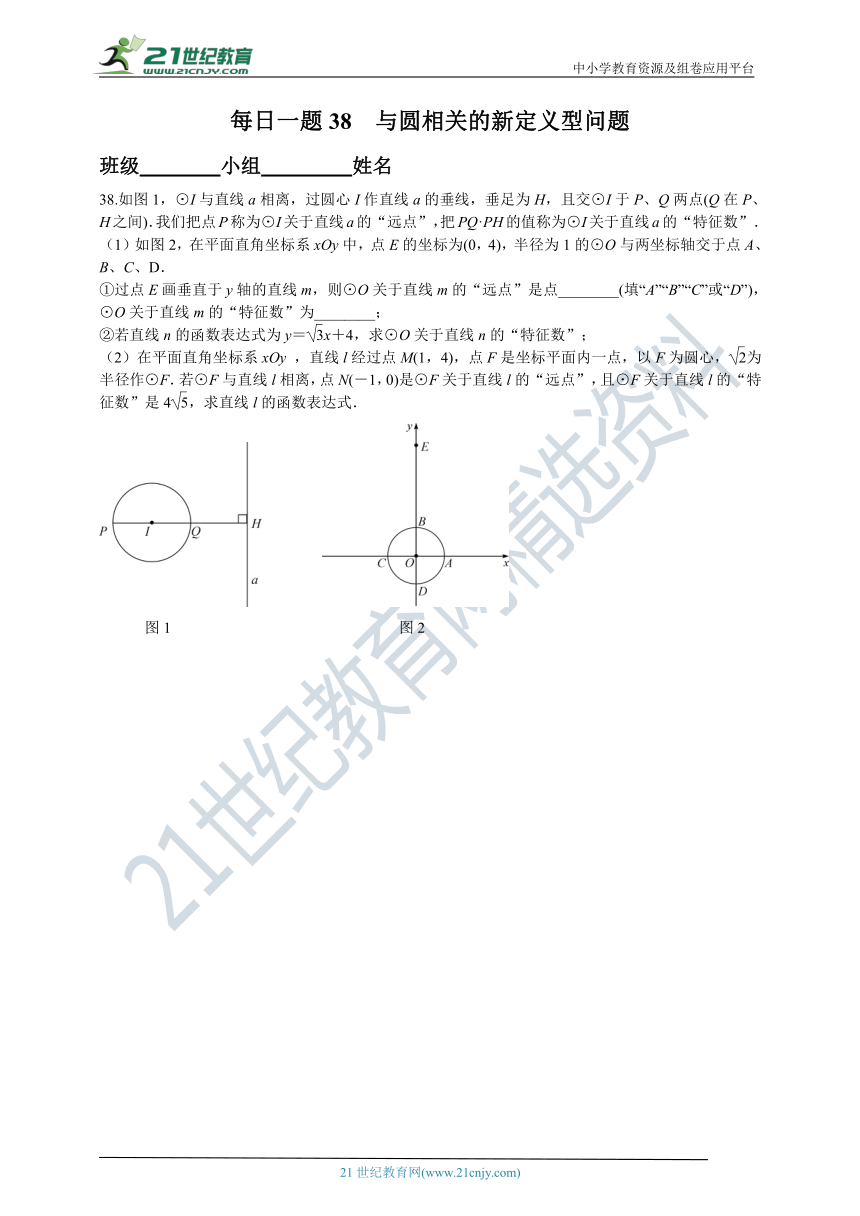
38.如图1,⊙I与直线a相离,过圆心I作直线a的垂线,垂足为H,且交⊙I于P、Q两点(Q在P、H之间).我们把点P称为⊙I关于直线a的“远点”,把PQ·PH的值称为⊙I关于直线a的“特征数”.
(1)如图2,在平面直角坐标系xOy中,点E的坐标为(0,4),半径为1的⊙O与两坐标轴交于点A、B、C、D.
①过点E画垂直于y轴的直线m,则⊙O关于直线m的“远点”是点________(填“A”“B”“C”或“D”),⊙O关于直线m的“特征数”为________;
②若直线n的函数表达式为y=x+4,求⊙O关于直线n的“特征数”;
(2)在平面直角坐标系xOy ,直线l经过点M(1,4),点F是坐标平面内一点,以F为圆心,为半径作⊙F.若⊙F与直线l相离,点N(-1,0)是⊙F关于直线l的“远点”,且⊙F关于直线l的“特征数”是4,求直线l的函数表达式.
INCLUDEPICTURE"20CZSX15.TIF" INCLUDEPICTURE "C:\\Users\\chenxi\\Desktop\\20CZSX15.TIF" \* MERGEFORMATINET INCLUDEPICTURE "C:\\Users\\余中华\\Desktop\\20CZSX15.TIF" \* MERGEFORMATINET INCLUDEPICTURE "C:\\Users\\鱼\\Desktop\\20CZSX15.TIF" \* MERGEFORMATINET INCLUDEPICTURE"20CZSX16.TIF" INCLUDEPICTURE "C:\\Users\\chenxi\\Desktop\\20CZSX16.TIF" \* MERGEFORMATINET INCLUDEPICTURE "C:\\Users\\余中华\\Desktop\\20CZSX16.TIF" \* MERGEFORMATINET INCLUDEPICTURE "C:\\Users\\鱼\\Desktop\\20CZSX16.TIF" \* MERGEFORMATINET
图1 图2
每日一题39 与圆相关的新定义型问题
班级 小组 姓名
39.已知平面图形S,点P、Q是S上任意两点,我们把线段PQ的长度的最大值称为平面图形S的“宽距”.例如,正方形的宽距等于它的对角线的长度.
(1)写出下列图形的宽距:①半径为1的圆:________;
②如图1,上方是半径为1的半圆,下方是正方形的三条边的“窗户形”:________;
(2)如图2,在平面直角坐标系中,已知点A(-1,0)、B(1,0),C是坐标平面内的点,连接AB、BC、CA所形成的图形为S,记S的宽距为d.
①若d=2,用直尺和圆规画出点C所在的区域并求它的面积(所在区域用阴影表示);
②若点C在⊙M上运动,⊙M的半径为1,圆心M在过点(0,2)且与y轴垂直的直线上.对于⊙M上的任意点C,都有5≤d≤8,直接写出圆心M的横坐标x的取值范围.
每日一题40 与圆相关的新定义型问题
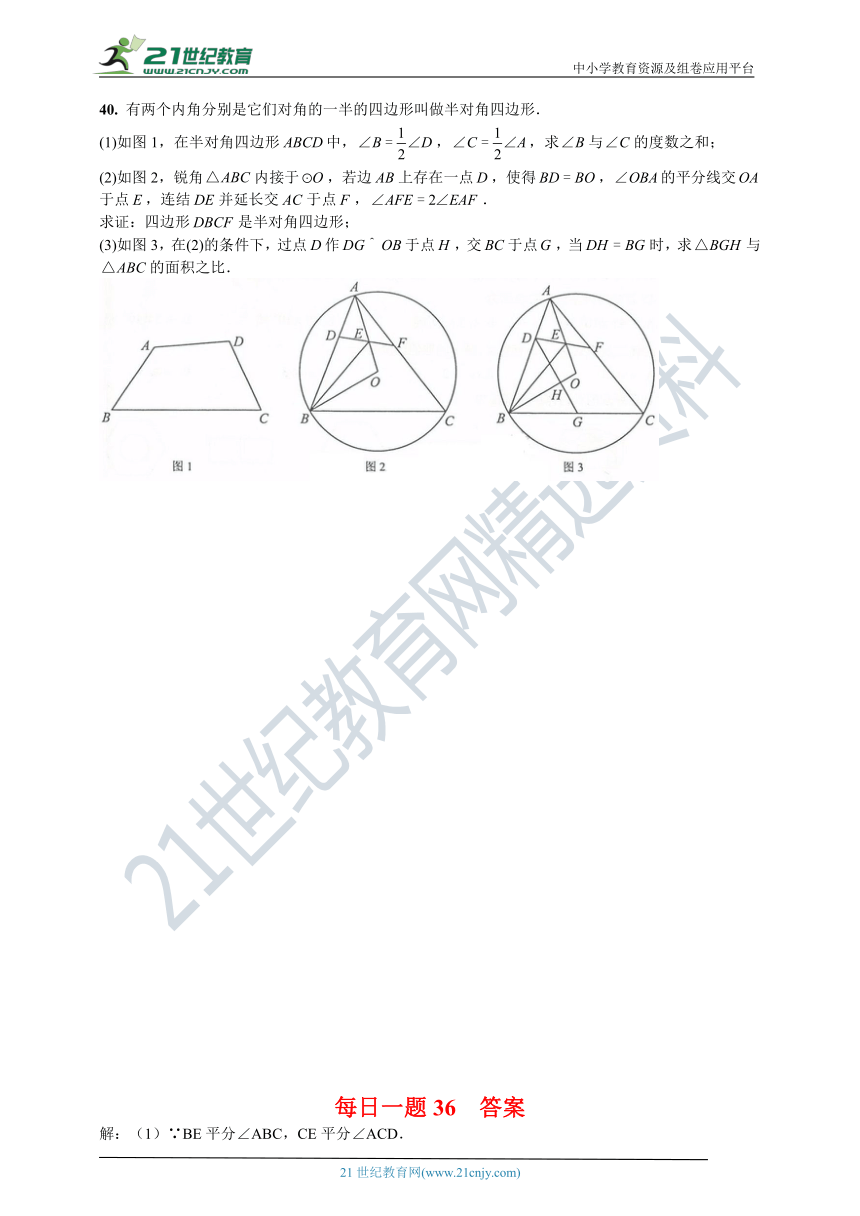
40. 有两个内角分别是它们对角的一半的四边形叫做半对角四边形.
(1)如图1,在半对角四边形中,,,求与的度数之和;
(2)如图2,锐角内接于,若边上存在一点,使得,的平分线交于点,连结并延长交于点,.
求证:四边形是半对角四边形;
(3)如图3,在(2)的条件下,过点作于点,交于点,当时,求与的面积之比.
每日一题36 答案
解:(1)∵BE平分∠ABC,CE平分∠ACD.
∴∠E=∠ECD-∠EBD=(∠ACD-∠ABC)=∠A=a
(2)如图,延长BC到点T.∵四边形FBCD内接于⊙O,
∴∠FDC+∠FBC=180°,又∵∠FDE+∠FDC=180°,∴∠FDE=∠FBC,∵DF平分∠ADE,
∴∠ADF=∠FDE,∵∠ADF=∠ABF,∴∠ABF=∠FBC,∴BE是∠ABC的平分线,
∵=,∴∠ACD=∠BFD,∵∠BFD+∠BCD=180°,
∠DCT+∠BCD=180°,∴∠DCT=∠BFD,∴∠ACD=∠DCT,
∴CE是△ABC的外角平分线,∴∠BEC是△ABC中∠BAC的遥望角.
(3)①如图,连结CF.
∵∠BEC是△ABC中∠BAC的遥望角,∴∠BAC=2∠BEC,
∵∠BFC=∠BAC,∴∠BFC=2∠BEC,
∵∠BFC=∠BEC+∠FCE,∴∠BEC=∠FCE,∵∠FCE=∠FAD,
∴∠BEC=∠FAD,又∵∠FDE=∠FDA,FD=FD,∴△FDE≌△FDA(AAS),
∴DE=AD,∵∠AED=∠DAE,∵AC是⊙O的直径
∴∠ADC=90°,∴∠AED+∠DAE=90°,∴∠AED=∠DAE=45°.
②如图,过点A作AG⊥BE于点G,过点F作FM⊥CE于点M.
∵AC是⊙O的直径,∴∠ABC=90°,∵BE平分∠ABC,∴∠FAC=∠EBC=∠ABC=45°,
∵∠AED=45°,∴∠AED=∠FAC,∵∠FED=∠FAD,∴∠AED-∠FED=∠FAC-∠FAD,
∴∠AEG=∠CAD,∴∠EGA=∠ADC=90°,∴△EGA∽△ADC,
∴AE:AC=AG:CD∵在Rt△ABG中,AG=AB=,
在Rt△ADE中,AE=AD,∴AD:AC=,在Rt△ADC中,
AD2+DC2=AC2,∴设AD=4x,AC=5x,则有(4x)2+52=(5x)2,
∴x=,∴ED=AD=,∴CE=CD+DE=,∵∠BEC=∠FCE,∴FC=FE,∵FM⊥CE,∴EM=CE=,∴DM=DE-EM=,
∵∠FDM=45° ,∴FM=DM=,
∴S△DEF=DE·FM=.
每日一题37 答案
解: (1)平行;P3;
(2)如图,线段AB在直线上,平移之后与圆相交,得到的弦为CD,CD∥AB,过点O作OE⊥AB于点E,交弦CD于点F,OF⊥CD,令,直线与x轴交点为(-2,0),直线与x轴夹角为60°,∴.
由垂径定理得:,∴;
(3)线段AB的位置变换,可以看作是以点A为圆心,半径为1的圆,只需在⊙O内找到与之平行,且长度为1的弦即可;
点A到O的距离为.
如图,平移距离的最小值即点A到⊙O的最小值:;
如图,由平移距离可知,AA 的长度的最小值即为平移距离,因此当且仅当AA =AA 时,平移距离最大,如图所示:
由题意可知:△AA O≌△AA O,可得∠AOA =120°,在Rt△A OC中,A C=,所以AA =.
∴.
每日一题38 答案
解:(1)根据定义得⊙O关于直线m的远点是D;(2)如图1,圆O关于直线m的特征数为DB×DE=[1-(-1)]·[4-(-1)]=2×5=10.
②如图2,过O点作OA1⊥直线n于A1,延长A1O交圆O于点B1,设 与y轴交于点C1,∴OC1=4
∵ ∴直线与x轴的所夹锐角为60°.∴∠A1C1O=90°-60°=30°
在Rt△A1C1O中,A1O= C1O=2
∵OB1=1,∴⊙O关于直线n的特征数=2B1O×A1B1=2(2+1)=6
(2)如图3,设过M的直线l解析式为y=k1x+b1
∴4=k1+b1,即k1=4-b1,∴l的解析式为y=(4-b1)x+b1
设⊙F与NF所在直线交D1,NF的延长线交y=k1x+b1于E1
∵⊙F的半径为 ,∴NF=FD1=
∵⊙F关于直线l的“特征数”是
∴ND1·NE1= 即
由点N到直线l的距离公式得.
∴b1=7或 经检验,b1=7或都是原方程的解,且符合题意.
当b1=7时,k1=-3,此时直线l的函数表达式为y=-3x+7.
当b1= 时,k1=此时直线l的函数表达式为.
综上所述,此时直线l的函数表达式为y=-3x+7或.
图1 图2 图3
每日一题39 答案
解:(1)①2(直径是圆的宽距);②+1.(如答图1,点A与半圆圆心的连线与半圆相交于点D,则AD的长最大)
(2)①如答图2所示,分别以A、B为圆心,以AB为半径所作的圆心角为120°的两条弧所形成的阴影部分即为点C所在的区域. S阴影=2(-)=.
②2-1≤x≤3-1或1-3≤x≤1-2.
每日一题40 答案
【解析】(1)在半对角四边形ABCD中,∠B=∠D,∠C=∠A,
∵∠A+∠B+∠C+∠D=360°,∴3∠B+3∠C=360°.∴∠B+∠C=120°,
即∠B与∠C的和为120°.
(2)在△BED和△BEO中,
, ∴△BED≌△BEO(SAS).∴∠BDE=∠BOE,
又∵∠BCF=∠BOE, ∴∠BCF=∠BDE.
如图,连接OC,设∠EAF=a,则∠AFE=2a.
∴∠EFC=180°-∠AFE=180°-2a.
∵OA=OC, ∴∠OAC=∠OCA=a.
∴∠AOC=180°-2a. ∴∠ABC=∠AOC=∠EFC,
∴四边形DBCF是半对角四边形.
(3)如图,作OM⊥BC于点M.∵四边形DBCF是半对角四边形.
∴∠ABC+∠ACB=120°,∴∠BAC=60°,∴∠BOC=2∠BAC=120°,
∵OB=OC, ∴∠OBC=∠OBC=30°, ∴BC=2BM=BO=BD.
∵DG⊥OB,∴∠HGB=∠BAC=60°.
∵∠DBG=∠CBA,∴△DBG∽△CBA.
∴,
∵DH=BG,BG=2HG, ∴DG=3HG,
∴, ∴.
图2
图1
第39题答图1
第39题答图2
第39题答图3 第39题答图4
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
每日一题36 与圆相关的新定义型问题
班级 小组 姓名
36.定义:三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角.
(1)如图1,∠E是△ABC中∠A的遥望角,若∠A=a,请用含a的代数式表示∠E.
(2)如图2,四边形ABCD内接于⊙O,=,四边形ABCD的外角平分线DF交⊙O于点F,连结BF并延长交CD的延长线于点E.求证:∠BEC是△ABC中∠BAC的遥望角.
(3)如图3,在(2)的条件下,连结AE,AF,若AC是⊙O的直径.
①求∠AED的度数;
②若AB=8,CD=5,求△DEF的面积.
每日一题37 与圆相关的新定义型问题
班级 小组 姓名
37.在平面直角坐标系xOy中,⊙O的半径为1,A,B为⊙O外两点,AB=1.给出如下定义:平移线段AB,得到⊙O的弦A B (A ,B 分别为点A,B的对应点),线段AA 长度的最小值称为线段AB到⊙O的“平移距离”.
(1)如图,平移线段AB到⊙O的长度为1的弦和,则这两条弦的位置关系是 ;在点中,连接点A与点 的线段的长度等于线段AB到⊙O的“平移距离”;
(2)若点A,B都在直线上,记线段AB到⊙O的“平移距离”为,求的最小值;
(3)若点A的坐标为,记线段AB到⊙O的“平移距离”为,直接写出的取值范围.
每日一题38 与圆相关的新定义型问题
班级 小组 姓名
38.如图1,⊙I与直线a相离,过圆心I作直线a的垂线,垂足为H,且交⊙I于P、Q两点(Q在P、H之间).我们把点P称为⊙I关于直线a的“远点”,把PQ·PH的值称为⊙I关于直线a的“特征数”.
(1)如图2,在平面直角坐标系xOy中,点E的坐标为(0,4),半径为1的⊙O与两坐标轴交于点A、B、C、D.
①过点E画垂直于y轴的直线m,则⊙O关于直线m的“远点”是点________(填“A”“B”“C”或“D”),⊙O关于直线m的“特征数”为________;
②若直线n的函数表达式为y=x+4,求⊙O关于直线n的“特征数”;
(2)在平面直角坐标系xOy ,直线l经过点M(1,4),点F是坐标平面内一点,以F为圆心,为半径作⊙F.若⊙F与直线l相离,点N(-1,0)是⊙F关于直线l的“远点”,且⊙F关于直线l的“特征数”是4,求直线l的函数表达式.
INCLUDEPICTURE"20CZSX15.TIF" INCLUDEPICTURE "C:\\Users\\chenxi\\Desktop\\20CZSX15.TIF" \* MERGEFORMATINET INCLUDEPICTURE "C:\\Users\\余中华\\Desktop\\20CZSX15.TIF" \* MERGEFORMATINET INCLUDEPICTURE "C:\\Users\\鱼\\Desktop\\20CZSX15.TIF" \* MERGEFORMATINET INCLUDEPICTURE"20CZSX16.TIF" INCLUDEPICTURE "C:\\Users\\chenxi\\Desktop\\20CZSX16.TIF" \* MERGEFORMATINET INCLUDEPICTURE "C:\\Users\\余中华\\Desktop\\20CZSX16.TIF" \* MERGEFORMATINET INCLUDEPICTURE "C:\\Users\\鱼\\Desktop\\20CZSX16.TIF" \* MERGEFORMATINET
图1 图2
每日一题39 与圆相关的新定义型问题
班级 小组 姓名
39.已知平面图形S,点P、Q是S上任意两点,我们把线段PQ的长度的最大值称为平面图形S的“宽距”.例如,正方形的宽距等于它的对角线的长度.
(1)写出下列图形的宽距:①半径为1的圆:________;
②如图1,上方是半径为1的半圆,下方是正方形的三条边的“窗户形”:________;
(2)如图2,在平面直角坐标系中,已知点A(-1,0)、B(1,0),C是坐标平面内的点,连接AB、BC、CA所形成的图形为S,记S的宽距为d.
①若d=2,用直尺和圆规画出点C所在的区域并求它的面积(所在区域用阴影表示);
②若点C在⊙M上运动,⊙M的半径为1,圆心M在过点(0,2)且与y轴垂直的直线上.对于⊙M上的任意点C,都有5≤d≤8,直接写出圆心M的横坐标x的取值范围.
每日一题40 与圆相关的新定义型问题
40. 有两个内角分别是它们对角的一半的四边形叫做半对角四边形.
(1)如图1,在半对角四边形中,,,求与的度数之和;
(2)如图2,锐角内接于,若边上存在一点,使得,的平分线交于点,连结并延长交于点,.
求证:四边形是半对角四边形;
(3)如图3,在(2)的条件下,过点作于点,交于点,当时,求与的面积之比.
每日一题36 答案
解:(1)∵BE平分∠ABC,CE平分∠ACD.
∴∠E=∠ECD-∠EBD=(∠ACD-∠ABC)=∠A=a
(2)如图,延长BC到点T.∵四边形FBCD内接于⊙O,
∴∠FDC+∠FBC=180°,又∵∠FDE+∠FDC=180°,∴∠FDE=∠FBC,∵DF平分∠ADE,
∴∠ADF=∠FDE,∵∠ADF=∠ABF,∴∠ABF=∠FBC,∴BE是∠ABC的平分线,
∵=,∴∠ACD=∠BFD,∵∠BFD+∠BCD=180°,
∠DCT+∠BCD=180°,∴∠DCT=∠BFD,∴∠ACD=∠DCT,
∴CE是△ABC的外角平分线,∴∠BEC是△ABC中∠BAC的遥望角.
(3)①如图,连结CF.
∵∠BEC是△ABC中∠BAC的遥望角,∴∠BAC=2∠BEC,
∵∠BFC=∠BAC,∴∠BFC=2∠BEC,
∵∠BFC=∠BEC+∠FCE,∴∠BEC=∠FCE,∵∠FCE=∠FAD,
∴∠BEC=∠FAD,又∵∠FDE=∠FDA,FD=FD,∴△FDE≌△FDA(AAS),
∴DE=AD,∵∠AED=∠DAE,∵AC是⊙O的直径
∴∠ADC=90°,∴∠AED+∠DAE=90°,∴∠AED=∠DAE=45°.
②如图,过点A作AG⊥BE于点G,过点F作FM⊥CE于点M.
∵AC是⊙O的直径,∴∠ABC=90°,∵BE平分∠ABC,∴∠FAC=∠EBC=∠ABC=45°,
∵∠AED=45°,∴∠AED=∠FAC,∵∠FED=∠FAD,∴∠AED-∠FED=∠FAC-∠FAD,
∴∠AEG=∠CAD,∴∠EGA=∠ADC=90°,∴△EGA∽△ADC,
∴AE:AC=AG:CD∵在Rt△ABG中,AG=AB=,
在Rt△ADE中,AE=AD,∴AD:AC=,在Rt△ADC中,
AD2+DC2=AC2,∴设AD=4x,AC=5x,则有(4x)2+52=(5x)2,
∴x=,∴ED=AD=,∴CE=CD+DE=,∵∠BEC=∠FCE,∴FC=FE,∵FM⊥CE,∴EM=CE=,∴DM=DE-EM=,
∵∠FDM=45° ,∴FM=DM=,
∴S△DEF=DE·FM=.
每日一题37 答案
解: (1)平行;P3;
(2)如图,线段AB在直线上,平移之后与圆相交,得到的弦为CD,CD∥AB,过点O作OE⊥AB于点E,交弦CD于点F,OF⊥CD,令,直线与x轴交点为(-2,0),直线与x轴夹角为60°,∴.
由垂径定理得:,∴;
(3)线段AB的位置变换,可以看作是以点A为圆心,半径为1的圆,只需在⊙O内找到与之平行,且长度为1的弦即可;
点A到O的距离为.
如图,平移距离的最小值即点A到⊙O的最小值:;
如图,由平移距离可知,AA 的长度的最小值即为平移距离,因此当且仅当AA =AA 时,平移距离最大,如图所示:
由题意可知:△AA O≌△AA O,可得∠AOA =120°,在Rt△A OC中,A C=,所以AA =.
∴.
每日一题38 答案
解:(1)根据定义得⊙O关于直线m的远点是D;(2)如图1,圆O关于直线m的特征数为DB×DE=[1-(-1)]·[4-(-1)]=2×5=10.
②如图2,过O点作OA1⊥直线n于A1,延长A1O交圆O于点B1,设 与y轴交于点C1,∴OC1=4
∵ ∴直线与x轴的所夹锐角为60°.∴∠A1C1O=90°-60°=30°
在Rt△A1C1O中,A1O= C1O=2
∵OB1=1,∴⊙O关于直线n的特征数=2B1O×A1B1=2(2+1)=6
(2)如图3,设过M的直线l解析式为y=k1x+b1
∴4=k1+b1,即k1=4-b1,∴l的解析式为y=(4-b1)x+b1
设⊙F与NF所在直线交D1,NF的延长线交y=k1x+b1于E1
∵⊙F的半径为 ,∴NF=FD1=
∵⊙F关于直线l的“特征数”是
∴ND1·NE1= 即
由点N到直线l的距离公式得.
∴b1=7或 经检验,b1=7或都是原方程的解,且符合题意.
当b1=7时,k1=-3,此时直线l的函数表达式为y=-3x+7.
当b1= 时,k1=此时直线l的函数表达式为.
综上所述,此时直线l的函数表达式为y=-3x+7或.
图1 图2 图3
每日一题39 答案
解:(1)①2(直径是圆的宽距);②+1.(如答图1,点A与半圆圆心的连线与半圆相交于点D,则AD的长最大)
(2)①如答图2所示,分别以A、B为圆心,以AB为半径所作的圆心角为120°的两条弧所形成的阴影部分即为点C所在的区域. S阴影=2(-)=.
②2-1≤x≤3-1或1-3≤x≤1-2.
每日一题40 答案
【解析】(1)在半对角四边形ABCD中,∠B=∠D,∠C=∠A,
∵∠A+∠B+∠C+∠D=360°,∴3∠B+3∠C=360°.∴∠B+∠C=120°,
即∠B与∠C的和为120°.
(2)在△BED和△BEO中,
, ∴△BED≌△BEO(SAS).∴∠BDE=∠BOE,
又∵∠BCF=∠BOE, ∴∠BCF=∠BDE.
如图,连接OC,设∠EAF=a,则∠AFE=2a.
∴∠EFC=180°-∠AFE=180°-2a.
∵OA=OC, ∴∠OAC=∠OCA=a.
∴∠AOC=180°-2a. ∴∠ABC=∠AOC=∠EFC,
∴四边形DBCF是半对角四边形.
(3)如图,作OM⊥BC于点M.∵四边形DBCF是半对角四边形.
∴∠ABC+∠ACB=120°,∴∠BAC=60°,∴∠BOC=2∠BAC=120°,
∵OB=OC, ∴∠OBC=∠OBC=30°, ∴BC=2BM=BO=BD.
∵DG⊥OB,∴∠HGB=∠BAC=60°.
∵∠DBG=∠CBA,∴△DBG∽△CBA.
∴,
∵DH=BG,BG=2HG, ∴DG=3HG,
∴, ∴.
图2
图1
第39题答图1
第39题答图2
第39题答图3 第39题答图4
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
