浙教版九上数学每日一题46-50 几何新定义型问题(含解析)
文档属性
| 名称 | 浙教版九上数学每日一题46-50 几何新定义型问题(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
每日一题46 几何新定义型问题
班级 小组 姓名
46.定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.
(1)如图1,在△ABC中,AB=AC,AD是△ABC的角平分线,E,F分别是BD,AD上的点.求证:四边形ABEF是邻余四边形;
(2)如图2,在5×4的方格纸中,A,B在格点上,请画出一个符合条件的邻余四边形ABEF,使AB是邻余线,E,F在格点上;
(3)如图3,在(1)的条件下,取EF中点M,连接DM并延长交AB于点Q,延长EF交AC于点N.若N为AC的中点,DE=2BE,QB=3,求邻余线AB的长.
每日一题47 几何新定义型问题
班级 小组 姓名
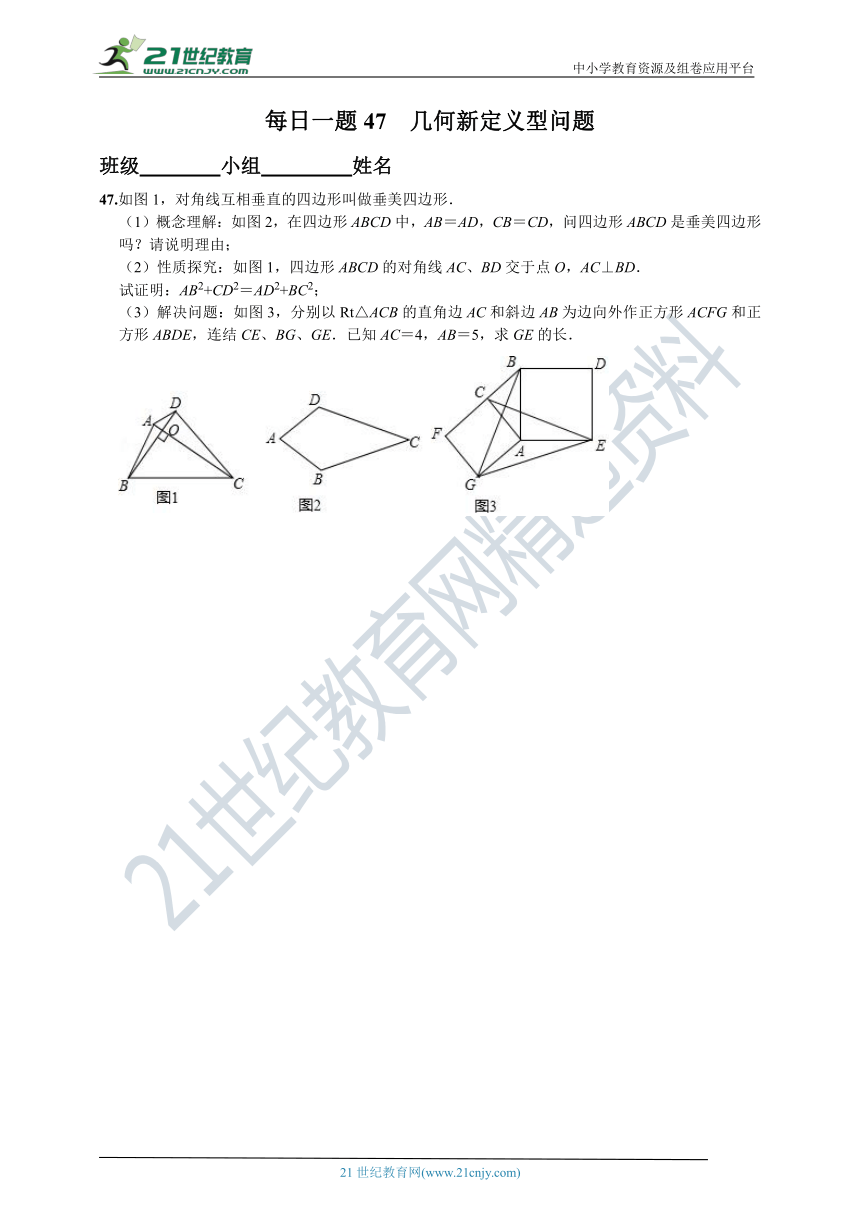
47.如图1,对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由;
(2)性质探究:如图1,四边形ABCD的对角线AC、BD交于点O,AC⊥BD.
试证明:AB2+CD2=AD2+BC2;
(3)解决问题:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结CE、BG、GE.已知AC=4,AB=5,求GE的长.
每日一题48 几何新定义型问题
班级 小组 姓名
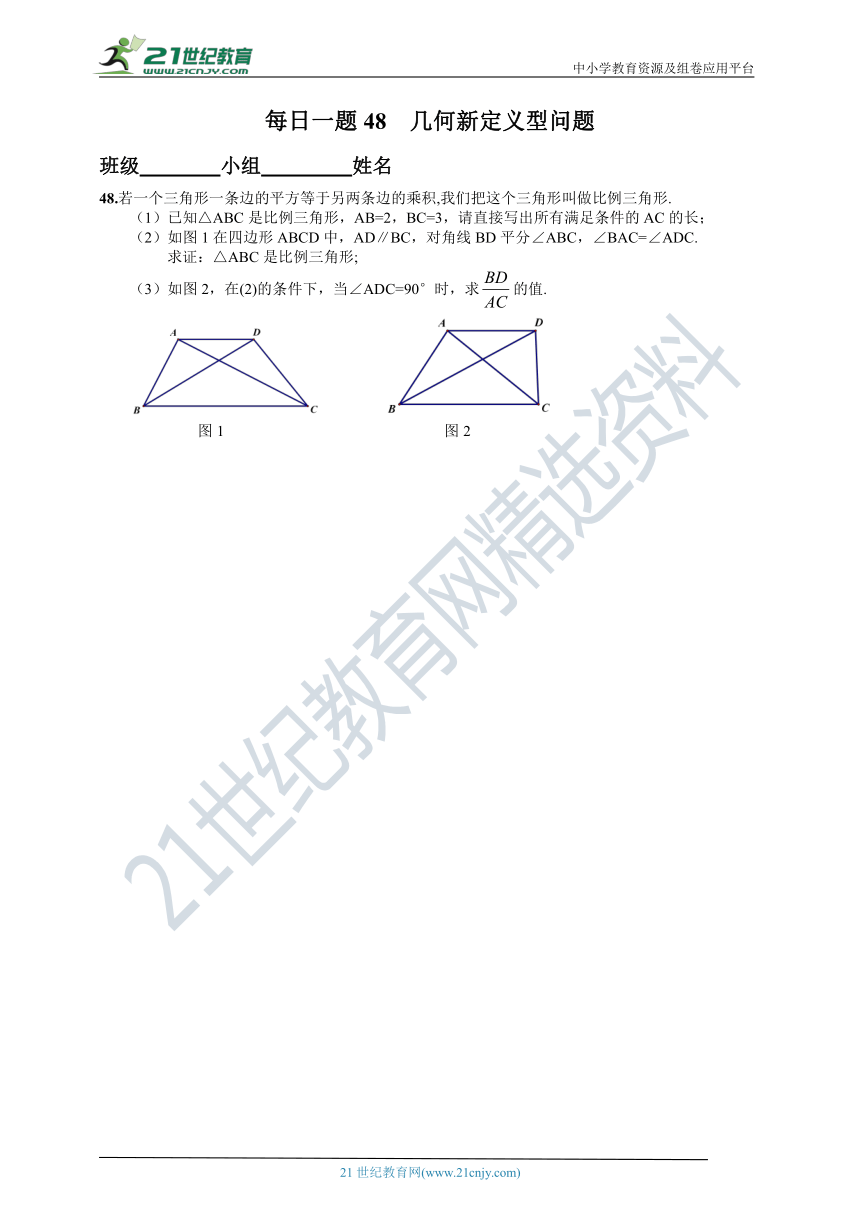
48.若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形.
(1)已知△ABC是比例三角形,AB=2,BC=3,请直接写出所有满足条件的AC的长;
(2)如图1在四边形ABCD中,AD∥BC,对角线BD平分∠ABC,∠BAC=∠ADC.
求证:△ABC是比例三角形;
(3)如图2,在(2)的条件下,当∠ADC=90°时,求的值.
图1 图2
每日一题49 几何新定义型问题
班级 小组 姓名
49.我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.
(1)概念理解:
如图1,在△ABC中,AC=6,BC=3,∠ACB=30°,试判断△ABC是否是“等高底”三角形,请说明理由.
(2)问题探究:
如图2,△ABC是“等高底”三角形,BC是“等底”,作△ABC关于BC所在直线的对称图形得到△A′BC,连结AA′交直线BC于点D.若点B是△AA′C的重心,求的值.
(3)应用拓展:
如图3,已知l1∥l2,l1与l2之间的距离为2.“等高底”△ABC的“等底”BC在直线l1上,点A在直线l2上,有一边的长是BC的倍.将△ABC绕点C按顺时针方向旋转45°得到△A′B′C,A′C所在直线交l2于点D.求CD的值.
图1 图2 图3
每日一题50 几何新定义型问题
班级 小组 姓名
50.如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形”。
(1) 若△ABC 是“准互余三角形”,∠C>90°, ∠A=60°,则∠B= ;
(2) 如图①,在Rt△ABC中,∠ACB=90。,AC=4, BC=5。若 AD 是∠BAC的平分线,不难证明△ABD是“准互余三角形”。试问在边BC上是否存在点E(异于点D), 使得△ABE也是“准互余三角形”?若存在,请求出BE的长;若不存在,请说明理由。
(3) 如图②,在四边形ABCD中,AB=7,CD=12,BD丄CD,∠ABD=2∠BCD,且△ABC是“准互余三角形”,求对角线AC的长。
每日一题46 答案
46. 解:(1)∵AB=AC,AD是△ABC的角平分线,∴AD⊥BC,∴∠ADB=90°
,∴∠DAB+∠DBA=90°,
∴∠FAB与∠EBA互余.∴四边形ABEF是邻余四边形;
(2)如图所示,四边形ABEF即为所求.(答案不唯一)
(3)∵AB=AC,AD是△ABC的角平分线,∴BD=CD,∵DE=2BE,
∴BD=CD=3BE,∴CE=CD+DE=5BE.
∵∠EDF=90°,M为EF的中点,∴DM=ME.
∴∠MDE=∠MED.
∵AB=AC,∴∠B=∠C,∴△DBQ∽△ECN,∴,
∵QB=3,∴NC=5,∵AN=CN,∴AC=2CN=10,∴AB=AC=10.
每日一题47 答案
解:(1)四边形ABCD是垂美四边形.
证明:∵AB=AD,∴点A在线段BD的垂直平分线上,
∵CB=CD,∴点C在线段BD的垂直平分线上,
∴直线AC是线段BD的垂直平分线,∴AC⊥BD,即四边形ABCD是垂美四边形;
(2)猜想结论:垂美四边形的两组对边的平方和相等.
如图2,已知四边形ABCD中,AC⊥BD,垂足为E,
求证:AD2+BC2=AB2+CD2
证明:∵AC⊥BD,∴∠AED=∠AEB=∠BEC=∠CED=90°,
由勾股定理得,AD2+BC2=AE2+DE2+BE2+CE2,AB2+CD2=AE2+BE2+CE2+DE2,
∴AD2+BC2=AB2+CD2; 故答案为:AD2+BC2=AB2+CD2.
(3)连接CG、BE,∵∠CAG=∠BAE=90°,
∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,
又∵AG=AC,AB=AE,∴△GAB≌△CAE(SAS),
∴∠ABG=∠AEC,又∠AEC+∠AME=90°,∴∠ABG+∠AME=90°,即CE⊥BG,
∴四边形CGEB是垂美四边形,
由(2)得,CG2+BE2=CB2+GE2,∵AC=4,AB=5,∴BC=3,CG=4,BE=5,
∴GE2=CG2+BE2﹣CB2=73,∴GE=.
每日一题48 答案
【解题过程】解:(1)或或。
(2)∵AD∥BC, ∴∠ACB=∠CAD
又∵∠BAC=∠ADC, ∴△ABC∽△DCA
∴,即CA2=BC·AD
∵AD∥BC,
∴∠ADB=∠CBD
∵BD平分∠ABC,
∴∠ABD=∠CBD
∴∠ADB=∠ABD
∴AB=AD
∴CA2=BC·AB,
∴△ABC是比例三角形
(3)如图,过点A作AH⊥BD于点H
∵AB=AD,
∴BH=BD.
∵AD∥BC,∠ADC=90°
∴∠BCD=90°
∴∠BHA=∠BCD=90°
又∵∠ABH=∠DBC,
∴△ABH∽△DBC
∴
∴AB·BC=DB·BH,
∴AB·BC=BD2
又∵AB·BC=AC2,
∴BD2=AC2
∴
每日一题49 答案
【解答过程】(1)如图1,过点A作AD上直线CD于点D,
∴△ADC为直角三角形,∠ADC=90°
∴∠ACB=30°,AC=6,∴AD==3 ∴AD=BC=3
即是“等高底”三角形.
(2)如图2,∵△ABC是“等高底”三角形,BC是“等底”,∴AD=BC
∵△A′BC与与△ABC关于直线BC对称,∴∠ADC=90°
∵点B是△AA′C的重心,∴BC=2BD。设BD=x,则AD=BC=2x,∴CD=3x
∴由勾股定理得AC=x,∴
(3)①当AB=BC时,
Ⅰ.如图3,作AE⊥l1于点E,DF⊥AC于点F,
“等高底”△ABC的“等底”为BC,l1∥l2. l1与l2之间的距离为2,AB=BC
∴BC=AE=2,AB= ∴BE=2,即EC=4,∴AC=
∵△ABC绕点C按顺时针方向旋转45°得到△A′B′C,∴∠CDF=45° 设DF=CF=x
∵ l1∥l2,∴∠ACE=∠DAF,∴,即.
∴AC=3x=,可得x=,∴CD=
Ⅱ.如图4,此时△ABC是等腰直角三角形,
∵△ABC绕点C按顺时针方向旋转45°得到△A′B′C,∴△ACD是等腰直角三角形,
∴CD=AC=
②当AC=BC时,
Ⅰ.如图5,此时△ABC是等腰直角三角形,∴△ABC绕点C按顺时针方向旋转45°得到△A′B′C时,
点A′在直线l1上。∴A′C∥l2,即直线A′C与l2无交点
综上,CD的值为,,2 【其他不同解法,请酌情给分】
49题图1 49题图2 49题图3
49题图4 49题图5 49题图6
每日一题50 答案
解:(1)由“准互余三角形”定义可知:若△ABC是“准互余三角形”,又∠C>90°,则有2∠A+∠B= 90°或 2∠B+∠A=90°,又因∠A=60°,则 2∠A+∠B= 90°不成立,
即代入 2∠B+∠A= 90°可得∠B=15°.
(2) 存在,
∵点 E 在 BC 边 上 , ∴ ∠ AEB > 90 ° ,
∴2∠BAE+∠B=90° 或 2∠B +∠BAE=90° ,
∵点 E(异于点 D),∴2∠BAE+∠B=90°不成立.
由图可知:在 Rt△ABC 中可得∠BAE+∠EAC+∠B=90° ,
又由“准互余三角形”定义可知: 2∠B +∠BAE=90°,∴∠B=∠EAC,
∴△ABC∽△EAC (AA),∴,
∵AC=4, BC=5, ∴, ∴
(3) 由题意可知:∵∠ABC=∠ABD+∠CBD=2∠BCD+∠CBD=90°+∠CBD. ∴∠ABC>90°,
∴本题分 2 类讨论:
①因△ABC 为“准互余三角形”,则∠BAC+2∠ACB=90°,设∠ACD=x,∠ACB=y,则可得:∠BAC=90°-2y,∠ABD=2x+2y,则∠AEB=90°-2x,又因为在△CDE 中,∠AEB=90°-x,则x=0°,与构成四边形矛盾,舍去.
②因 2∠BAC+∠ACB=90°,设∠BAC=x,则∠ACB=90°-2x,则∠ABC=90°+x,过点 B 作 BE⊥AB,易得△CBE∽△CAB,即CB2= CE× CA ,由∠ABD=2∠BCD 易得∠BAC=∠BCD,则△BAE∽△DCB,设 AE=7a,则 CB=12a,则易得 CE=9a,可解得 ,勾股定理得:,∴AC=16a=20.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
每日一题46 几何新定义型问题
班级 小组 姓名
46.定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.
(1)如图1,在△ABC中,AB=AC,AD是△ABC的角平分线,E,F分别是BD,AD上的点.求证:四边形ABEF是邻余四边形;
(2)如图2,在5×4的方格纸中,A,B在格点上,请画出一个符合条件的邻余四边形ABEF,使AB是邻余线,E,F在格点上;
(3)如图3,在(1)的条件下,取EF中点M,连接DM并延长交AB于点Q,延长EF交AC于点N.若N为AC的中点,DE=2BE,QB=3,求邻余线AB的长.
每日一题47 几何新定义型问题
班级 小组 姓名
47.如图1,对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由;
(2)性质探究:如图1,四边形ABCD的对角线AC、BD交于点O,AC⊥BD.
试证明:AB2+CD2=AD2+BC2;
(3)解决问题:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结CE、BG、GE.已知AC=4,AB=5,求GE的长.
每日一题48 几何新定义型问题
班级 小组 姓名
48.若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形.
(1)已知△ABC是比例三角形,AB=2,BC=3,请直接写出所有满足条件的AC的长;
(2)如图1在四边形ABCD中,AD∥BC,对角线BD平分∠ABC,∠BAC=∠ADC.
求证:△ABC是比例三角形;
(3)如图2,在(2)的条件下,当∠ADC=90°时,求的值.
图1 图2
每日一题49 几何新定义型问题
班级 小组 姓名
49.我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.
(1)概念理解:
如图1,在△ABC中,AC=6,BC=3,∠ACB=30°,试判断△ABC是否是“等高底”三角形,请说明理由.
(2)问题探究:
如图2,△ABC是“等高底”三角形,BC是“等底”,作△ABC关于BC所在直线的对称图形得到△A′BC,连结AA′交直线BC于点D.若点B是△AA′C的重心,求的值.
(3)应用拓展:
如图3,已知l1∥l2,l1与l2之间的距离为2.“等高底”△ABC的“等底”BC在直线l1上,点A在直线l2上,有一边的长是BC的倍.将△ABC绕点C按顺时针方向旋转45°得到△A′B′C,A′C所在直线交l2于点D.求CD的值.
图1 图2 图3
每日一题50 几何新定义型问题
班级 小组 姓名
50.如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形”。
(1) 若△ABC 是“准互余三角形”,∠C>90°, ∠A=60°,则∠B= ;
(2) 如图①,在Rt△ABC中,∠ACB=90。,AC=4, BC=5。若 AD 是∠BAC的平分线,不难证明△ABD是“准互余三角形”。试问在边BC上是否存在点E(异于点D), 使得△ABE也是“准互余三角形”?若存在,请求出BE的长;若不存在,请说明理由。
(3) 如图②,在四边形ABCD中,AB=7,CD=12,BD丄CD,∠ABD=2∠BCD,且△ABC是“准互余三角形”,求对角线AC的长。
每日一题46 答案
46. 解:(1)∵AB=AC,AD是△ABC的角平分线,∴AD⊥BC,∴∠ADB=90°
,∴∠DAB+∠DBA=90°,
∴∠FAB与∠EBA互余.∴四边形ABEF是邻余四边形;
(2)如图所示,四边形ABEF即为所求.(答案不唯一)
(3)∵AB=AC,AD是△ABC的角平分线,∴BD=CD,∵DE=2BE,
∴BD=CD=3BE,∴CE=CD+DE=5BE.
∵∠EDF=90°,M为EF的中点,∴DM=ME.
∴∠MDE=∠MED.
∵AB=AC,∴∠B=∠C,∴△DBQ∽△ECN,∴,
∵QB=3,∴NC=5,∵AN=CN,∴AC=2CN=10,∴AB=AC=10.
每日一题47 答案
解:(1)四边形ABCD是垂美四边形.
证明:∵AB=AD,∴点A在线段BD的垂直平分线上,
∵CB=CD,∴点C在线段BD的垂直平分线上,
∴直线AC是线段BD的垂直平分线,∴AC⊥BD,即四边形ABCD是垂美四边形;
(2)猜想结论:垂美四边形的两组对边的平方和相等.
如图2,已知四边形ABCD中,AC⊥BD,垂足为E,
求证:AD2+BC2=AB2+CD2
证明:∵AC⊥BD,∴∠AED=∠AEB=∠BEC=∠CED=90°,
由勾股定理得,AD2+BC2=AE2+DE2+BE2+CE2,AB2+CD2=AE2+BE2+CE2+DE2,
∴AD2+BC2=AB2+CD2; 故答案为:AD2+BC2=AB2+CD2.
(3)连接CG、BE,∵∠CAG=∠BAE=90°,
∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,
又∵AG=AC,AB=AE,∴△GAB≌△CAE(SAS),
∴∠ABG=∠AEC,又∠AEC+∠AME=90°,∴∠ABG+∠AME=90°,即CE⊥BG,
∴四边形CGEB是垂美四边形,
由(2)得,CG2+BE2=CB2+GE2,∵AC=4,AB=5,∴BC=3,CG=4,BE=5,
∴GE2=CG2+BE2﹣CB2=73,∴GE=.
每日一题48 答案
【解题过程】解:(1)或或。
(2)∵AD∥BC, ∴∠ACB=∠CAD
又∵∠BAC=∠ADC, ∴△ABC∽△DCA
∴,即CA2=BC·AD
∵AD∥BC,
∴∠ADB=∠CBD
∵BD平分∠ABC,
∴∠ABD=∠CBD
∴∠ADB=∠ABD
∴AB=AD
∴CA2=BC·AB,
∴△ABC是比例三角形
(3)如图,过点A作AH⊥BD于点H
∵AB=AD,
∴BH=BD.
∵AD∥BC,∠ADC=90°
∴∠BCD=90°
∴∠BHA=∠BCD=90°
又∵∠ABH=∠DBC,
∴△ABH∽△DBC
∴
∴AB·BC=DB·BH,
∴AB·BC=BD2
又∵AB·BC=AC2,
∴BD2=AC2
∴
每日一题49 答案
【解答过程】(1)如图1,过点A作AD上直线CD于点D,
∴△ADC为直角三角形,∠ADC=90°
∴∠ACB=30°,AC=6,∴AD==3 ∴AD=BC=3
即是“等高底”三角形.
(2)如图2,∵△ABC是“等高底”三角形,BC是“等底”,∴AD=BC
∵△A′BC与与△ABC关于直线BC对称,∴∠ADC=90°
∵点B是△AA′C的重心,∴BC=2BD。设BD=x,则AD=BC=2x,∴CD=3x
∴由勾股定理得AC=x,∴
(3)①当AB=BC时,
Ⅰ.如图3,作AE⊥l1于点E,DF⊥AC于点F,
“等高底”△ABC的“等底”为BC,l1∥l2. l1与l2之间的距离为2,AB=BC
∴BC=AE=2,AB= ∴BE=2,即EC=4,∴AC=
∵△ABC绕点C按顺时针方向旋转45°得到△A′B′C,∴∠CDF=45° 设DF=CF=x
∵ l1∥l2,∴∠ACE=∠DAF,∴,即.
∴AC=3x=,可得x=,∴CD=
Ⅱ.如图4,此时△ABC是等腰直角三角形,
∵△ABC绕点C按顺时针方向旋转45°得到△A′B′C,∴△ACD是等腰直角三角形,
∴CD=AC=
②当AC=BC时,
Ⅰ.如图5,此时△ABC是等腰直角三角形,∴△ABC绕点C按顺时针方向旋转45°得到△A′B′C时,
点A′在直线l1上。∴A′C∥l2,即直线A′C与l2无交点
综上,CD的值为,,2 【其他不同解法,请酌情给分】
49题图1 49题图2 49题图3
49题图4 49题图5 49题图6
每日一题50 答案
解:(1)由“准互余三角形”定义可知:若△ABC是“准互余三角形”,又∠C>90°,则有2∠A+∠B= 90°或 2∠B+∠A=90°,又因∠A=60°,则 2∠A+∠B= 90°不成立,
即代入 2∠B+∠A= 90°可得∠B=15°.
(2) 存在,
∵点 E 在 BC 边 上 , ∴ ∠ AEB > 90 ° ,
∴2∠BAE+∠B=90° 或 2∠B +∠BAE=90° ,
∵点 E(异于点 D),∴2∠BAE+∠B=90°不成立.
由图可知:在 Rt△ABC 中可得∠BAE+∠EAC+∠B=90° ,
又由“准互余三角形”定义可知: 2∠B +∠BAE=90°,∴∠B=∠EAC,
∴△ABC∽△EAC (AA),∴,
∵AC=4, BC=5, ∴, ∴
(3) 由题意可知:∵∠ABC=∠ABD+∠CBD=2∠BCD+∠CBD=90°+∠CBD. ∴∠ABC>90°,
∴本题分 2 类讨论:
①因△ABC 为“准互余三角形”,则∠BAC+2∠ACB=90°,设∠ACD=x,∠ACB=y,则可得:∠BAC=90°-2y,∠ABD=2x+2y,则∠AEB=90°-2x,又因为在△CDE 中,∠AEB=90°-x,则x=0°,与构成四边形矛盾,舍去.
②因 2∠BAC+∠ACB=90°,设∠BAC=x,则∠ACB=90°-2x,则∠ABC=90°+x,过点 B 作 BE⊥AB,易得△CBE∽△CAB,即CB2= CE× CA ,由∠ABD=2∠BCD 易得∠BAC=∠BCD,则△BAE∽△DCB,设 AE=7a,则 CB=12a,则易得 CE=9a,可解得 ,勾股定理得:,∴AC=16a=20.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
