浙教版九上数学每日一题51-55 拓展、探究、应用型问题(含解析)
文档属性
| 名称 | 浙教版九上数学每日一题51-55 拓展、探究、应用型问题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 11:15:28 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
每日一题51 拓展、探究、应用型问题
班级: 姓名:
51.
小明尝试用“观察—猜想—验证—应用”的方法进行探究,请你一起来解决问题.
(1)小明利用“几何画板”软件进行观察,测量,得到l随m变化的一组对应值,并在平面直角坐标系中以各对应值为坐标描点(如图2),请你在图2中连线,观察图象特征并猜想l与m可能满足的函数类别.
(2)小明结合图1,发现应用三角形和函数知识能验证(1)中的猜想,请你求出l关于m的函数表达式及自变量的取值范围,并求出线段EF长度的最小值.
(3)小明通过观察,推理,发现△BEF能成为直角三角形,请你求出当△BEF为直角三角形时m的值.
每日一题52 拓展、探究、应用型问题
班级: 姓名:
52.【性质探究】
如图,在矩形ABCD中,对角线AC,BD相交于点O,AE平分∠BAC,交BC于点E.作DF⊥AE于点H,分别交AB,AC于点F,G.
(1)判断△AFG的形状并说明理由;
(2)求证:BF=2OG.
【迁移应用】
(3)记△DGO的面积为S1,△DBF的面积为S2,当时,求的值;
【拓展延伸】
(4)若DF交射线AB于点F,【性质探究】中的其余条件不变,连结EF,当△BEF的面积为矩形ABCD面积的时,请直接写出tan∠BAE的值.
每日一题53 拓展、探究、应用型问题
班级: 姓名:
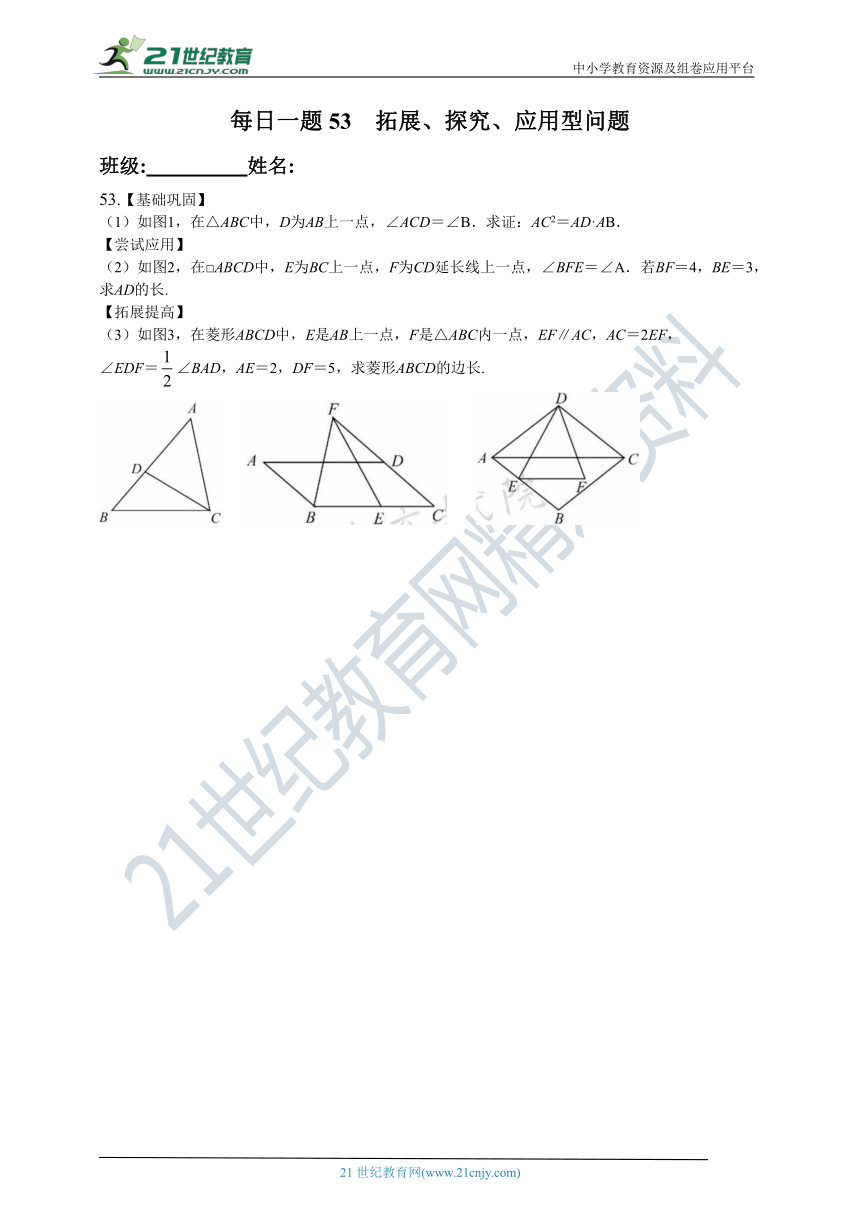
53.【基础巩固】
(1)如图1,在△ABC中,D为AB上一点,∠ACD=∠B.求证:AC2=AD·AB.
【尝试应用】
(2)如图2,在□ABCD中,E为BC上一点,F为CD延长线上一点,∠BFE=∠A.若BF=4,BE=3,求AD的长.
【拓展提高】
(3)如图3,在菱形ABCD中,E是AB上一点,F是△ABC内一点,EF∥AC,AC=2EF,
∠EDF=∠BAD,AE=2,DF=5,求菱形ABCD的边长.
每日一题54 拓展、探究、应用型问题
班级: 姓名:
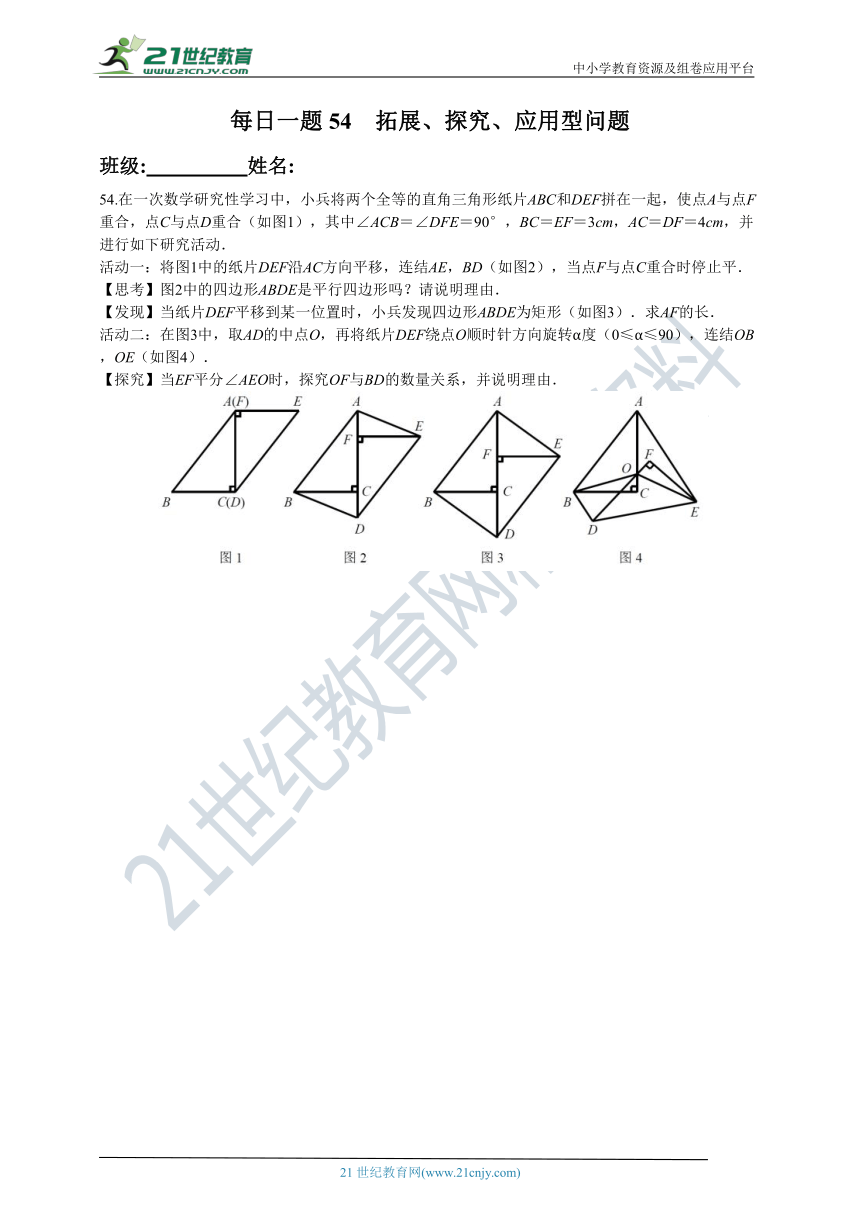
54.在一次数学研究性学习中,小兵将两个全等的直角三角形纸片ABC和DEF拼在一起,使点A与点F重合,点C与点D重合(如图1),其中∠ACB=∠DFE=90°,BC=EF=3cm,AC=DF=4cm,并进行如下研究活动.
活动一:将图1中的纸片DEF沿AC方向平移,连结AE,BD(如图2),当点F与点C重合时停止平.
【思考】图2中的四边形ABDE是平行四边形吗?请说明理由.
【发现】当纸片DEF平移到某一位置时,小兵发现四边形ABDE为矩形(如图3).求AF的长.
活动二:在图3中,取AD的中点O,再将纸片DEF绕点O顺时针方向旋转α度(0≤α≤90),连结OB,OE(如图4).
【探究】当EF平分∠AEO时,探究OF与BD的数量关系,并说明理由.
每日一题55 拓展、探究、应用型问题
班级: 姓名:
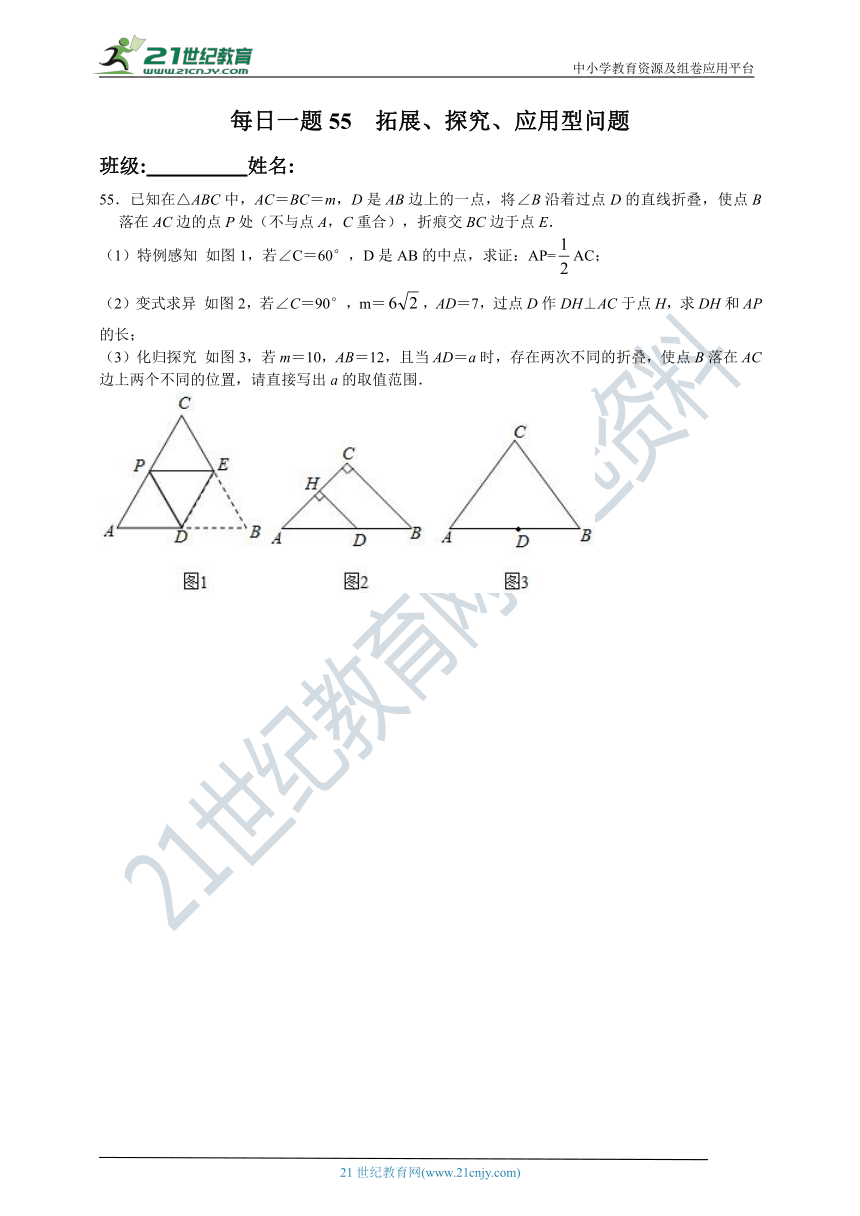
55.已知在△ABC中,AC=BC=m,D是AB边上的一点,将∠B沿着过点D的直线折叠,使点B落在AC边的点P处(不与点A,C重合),折痕交BC边于点E.
(1)特例感知 如图1,若∠C=60°,D是AB的中点,求证:AP=AC;
(2)变式求异 如图2,若∠C=90°,m=,AD=7,过点D作DH⊥AC于点H,求DH和AP的长;
(3)化归探究 如图3,若m=10,AB=12,且当AD=a时,存在两次不同的折叠,使点B落在AC边上两个不同的位置,请直接写出a的取值范围.
每日一题51 答案
解: (1)画图如下:猜想函数的类别为二次函数;
图1
(2)如图1,过点F,D分别作FG,DH垂直于y轴,垂足分别为G,H,则∠FGK=∠DHK=90 .
设FD交y轴于点K,∵D点与F点关于y轴上的K点成中心对称,∴KF=KD,
∵∠FKG=∠DKH,∴Rt△FGK≌Rt△DHK,∴FG=DH.
由yAC=-可知A(0,4) ,又∵B为(-2,0),∴yAB=2x+4,过点F作FR⊥x轴于点R,
∵D点的横坐标为m,∴F(-m,-2m+4),∴ER=2m,FR=-2m+4,
∵EF2=FR2+ER2,∴l=EF2=8m2-16m+16=8(m-1)2+8.
令-=0,解得x=1.5,∴,∴当m=1时,l的最小值为8.∴EF的最小值为2.
(3)分以下三种情形进行讨论:
①∠FBE为定角,不可能为直角;
②当∠BEF=90 ,E点与O点重合,D点与A点、F点重合,此时m=0;
③当∠BFE=90 时,如图2,
由于BF2+EF2=BE2, 由(2)得EF2=8m2﹣16m+16,又∵BR=﹣m+2,FR=﹣2m+4,
∴BF2=BR2+FR2=(﹣m+2)2+(﹣2m+4)2=5m2﹣20m+20,又∵BE2=(m+2)2,
∴(5m2﹣20m+8)+(8m2﹣16m+16)2=(m+2)2,化简得,3m2﹣10m+8=0,解得m1=,m2=2(不符题意,舍去),综上,当△BEF为直角三角形时,m=0或.
每日一题52 答案
解:如图1中,△AFG是等腰三角形.
理由:∵AE平分∠BAC,∴∠1=∠2,∵DF⊥AE,∴∠AHF=∠AHG=90°,
∵AH=AH,∴△AHF≌△AHG,∴AF=AG,∴△AFG是等腰三角形.
(2)证明:如图2中,过点O作OL∥AB交DF于L,则∠AFG=∠OLG.
∵AF=AG,∴∠AFG=∠AGF,∵∠AGF=∠OGL,∴∠OGL=∠OLG,∴OG=OL,
∵OL∥AB,∴△DLO∽△DFB,∴,
∵四边形ABCD是矩形,∴BD=2OD,∴BF=2OL,∴BF=2OG.
(3)解:如图3中,过点D作DK⊥AC于K,则∠DKA=∠CDA=90°,
∵∠DAK=∠CAD,∴△ADK∽△ACD,∴.
∵S1 OG DK,S2 BF AD,又∵BF=2OG,,
∴,设CD=2x,AC=3x,则AD=x,∴.
(4)解:设OG=a,AG=k.
①如图4中,连接EF,当点F在线段AB上时,点G在OA上.
∵AF=AG,BF=2OG,∴AF=AG=k,BF=2a,∴AB=k+2a,AC=2AO=2(k+a),
∴AD2=AC2﹣CD2=[2(k+a)]2﹣(k+2a)2=3k2+4ka,
∵∠ABE=∠DAF=90°,∠BAE=∠ADF,∴△ABE∽△DAF,∴,
∴,∴BE,由题意:102aAD (k+2a),
∴AD2=10ka,即10ka=3k2+4ka,∴k=2a,∴AD=2a,
∴BEa,AB=4a,∴tan∠BAE.
②如图5中,当点F在AB的延长线上时,点G在线段OC上,连接EF.
∵AF=AG,BF=2OG,∴AF=AG=k,BF=2a,∴AB=k﹣2a,AC=2(k﹣a),
∴AD2=AC2﹣CD2=[2(k﹣a)]2﹣(k﹣2a)2=3k2﹣4ka,
∵∠ABE=∠DAF=90°,∠BAE=∠ADF,∴△ABE∽△DAF,
∴,∴,∴BE,
由题意:102aAD (k﹣2a),∴AD2=10ka,即10ka=3k2﹣4ka,∴ka,∴ADa,∴BEa,ABa,∴tan∠BAE,
综上所述,tan∠BAE的值为或.
每日一题53 答案
53.解:(1)∵∠ACD=∠B,∠A=∠A,∴△ADC∽△ACB,∴AD:AC=AC:AB,∴AC2=AD·AB.
(2)∵四边形ABCD是平行四边形,
∴AD=BC,∠A=∠C,又∵∠BFE=∠A,∴∠BFE=∠C,又∵∠FBE=∠CBF,∴△BFE∽△BCF,∴BF2=BE·BC,
∴BC==,∴AD=
(3)如图,分别延长EF,DC相交于点G.∵四边形ABCD是菱形,
∴AB//DC,∠BAC=∠BAD,∴四边形AEGC为平行四边形,
∴AC=EG,CG=AE,∠EAC=∠G,∵∠EDF=∠BAC,
∴∠EDF=∠G,又∵∠DEF=∠GED,∴△EDF∽△EGD,
∴DE2=EF·EG,又∵EG=AC=2EF,∴DE2=2EF2,
∴DE=EF,又∵DG:DF=DE:EF,∴DG=DF=5,∴DC=DG-CG=5-2.
每日一题54 答案
解:【思考】四边形ABDE是平行四边形.
证明:如图,∵△ABC≌△DEF,∴AB=DE,∠BAC=∠EDF,
∴AB∥DE,∴四边形ABDE是平行四边形.
【发现】如图,连接BE交AD于点O,∵四边形ABDE为矩形,∴OA=OD=OB=OE,设AF=x cm,则OA=OE=(x+4),∴OF=OA﹣AF=2﹣x,
在Rt△OFE中,∵OF2+EF2=OE2,∴,
解得:x=,∴AF=cm.
【探究】BD=2OF,
证明:如图,延长OF交AE于点H,纸片DEF绕点O旋转前,四边形ABDE为矩形,∴OA=OB=OE=OD.纸片DEF绕点O旋转后,由旋转的性质可知,OA=OB=OE=OD,
∴∠OBD=∠ODB,∠OAE=∠OEA.∴∠ABD+∠BDE+∠DEA+∠EAB=360°,
∴∠ABD+∠BAE=180°,∴AE∥BD,∴∠OHE=∠ODB,
∵EF平分∠OEH,∴∠OEF=∠HEF.
∵∠EFO=∠EFH=90°,EF=EF, ∴△EFO≌△EFH(ASA),
∴EO=EH,FO=FH,∴∠EHO=∠EOH=∠OBD=∠ODB,
∴△EOH≌△OBD(AAS),∴BD=OH=2OF.
每日一题55 答案
【解答】(1)证明:∵AC=BC,∠C=60°,∴△ABC是等边三角形,∴AC=AB,∠A=60°,由题意,得DB=DP,DA=DB,∴DA=DP,∴△ADP使得等边三角形,
∴AP=AD=AB=AC.
(2)解:∵AC=BC=,∠C=90°,∴AB=12,
∵DH⊥AC,∴DH∥BC,∴△ADH∽△ABC,∴,
∵AD=7,∴,∴DH=,将∠B沿过点D的直线折叠,
情形一:当点B落在线段CH上的点P1处时,如图2﹣1中,
∵AB=12,∴DP1=DB=AB﹣AD=5,∴HP1=,
∴A1=AH+HP1=4,
情形二:当点B落在线段AH上的点P2处时,如图2﹣2中,
同法可证HP2=,∴AP2=AH﹣HP2=3,
综上所述,满足条件的AP的值为4或3.
(3)如图3中,过点C作CH⊥AB于H,过点D作DP⊥AC于P.
∵CA=CB,CH⊥AB,∴AH=HB=6,
∴CH==8,当DB=DP时,设BD=PD=x,则AD=12﹣x,
∵tanA=,∴,∴x=,
∴AD=AB﹣BD=,观察图形可知当6<a<时,存在两次不同的折叠,使点B落在AC边上两个不同的位置.
如图1,在平面直角坐标系中,△ABC的顶点A,C分别是直线 与坐标轴的交点,点B的坐标为(﹣2,0),点D是边AC上的一点,DE⊥BC于点E,点F在边AB上,且D,F两点关于y轴上的某点成中心对称,连结DF,EF.设点D的横坐标为m,EF2为l,请探究:
①线段EF长度是否有最小值;
②△BEF能否成为直角三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
每日一题51 拓展、探究、应用型问题
班级: 姓名:
51.
小明尝试用“观察—猜想—验证—应用”的方法进行探究,请你一起来解决问题.
(1)小明利用“几何画板”软件进行观察,测量,得到l随m变化的一组对应值,并在平面直角坐标系中以各对应值为坐标描点(如图2),请你在图2中连线,观察图象特征并猜想l与m可能满足的函数类别.
(2)小明结合图1,发现应用三角形和函数知识能验证(1)中的猜想,请你求出l关于m的函数表达式及自变量的取值范围,并求出线段EF长度的最小值.
(3)小明通过观察,推理,发现△BEF能成为直角三角形,请你求出当△BEF为直角三角形时m的值.
每日一题52 拓展、探究、应用型问题
班级: 姓名:
52.【性质探究】
如图,在矩形ABCD中,对角线AC,BD相交于点O,AE平分∠BAC,交BC于点E.作DF⊥AE于点H,分别交AB,AC于点F,G.
(1)判断△AFG的形状并说明理由;
(2)求证:BF=2OG.
【迁移应用】
(3)记△DGO的面积为S1,△DBF的面积为S2,当时,求的值;
【拓展延伸】
(4)若DF交射线AB于点F,【性质探究】中的其余条件不变,连结EF,当△BEF的面积为矩形ABCD面积的时,请直接写出tan∠BAE的值.
每日一题53 拓展、探究、应用型问题
班级: 姓名:
53.【基础巩固】
(1)如图1,在△ABC中,D为AB上一点,∠ACD=∠B.求证:AC2=AD·AB.
【尝试应用】
(2)如图2,在□ABCD中,E为BC上一点,F为CD延长线上一点,∠BFE=∠A.若BF=4,BE=3,求AD的长.
【拓展提高】
(3)如图3,在菱形ABCD中,E是AB上一点,F是△ABC内一点,EF∥AC,AC=2EF,
∠EDF=∠BAD,AE=2,DF=5,求菱形ABCD的边长.
每日一题54 拓展、探究、应用型问题
班级: 姓名:
54.在一次数学研究性学习中,小兵将两个全等的直角三角形纸片ABC和DEF拼在一起,使点A与点F重合,点C与点D重合(如图1),其中∠ACB=∠DFE=90°,BC=EF=3cm,AC=DF=4cm,并进行如下研究活动.
活动一:将图1中的纸片DEF沿AC方向平移,连结AE,BD(如图2),当点F与点C重合时停止平.
【思考】图2中的四边形ABDE是平行四边形吗?请说明理由.
【发现】当纸片DEF平移到某一位置时,小兵发现四边形ABDE为矩形(如图3).求AF的长.
活动二:在图3中,取AD的中点O,再将纸片DEF绕点O顺时针方向旋转α度(0≤α≤90),连结OB,OE(如图4).
【探究】当EF平分∠AEO时,探究OF与BD的数量关系,并说明理由.
每日一题55 拓展、探究、应用型问题
班级: 姓名:
55.已知在△ABC中,AC=BC=m,D是AB边上的一点,将∠B沿着过点D的直线折叠,使点B落在AC边的点P处(不与点A,C重合),折痕交BC边于点E.
(1)特例感知 如图1,若∠C=60°,D是AB的中点,求证:AP=AC;
(2)变式求异 如图2,若∠C=90°,m=,AD=7,过点D作DH⊥AC于点H,求DH和AP的长;
(3)化归探究 如图3,若m=10,AB=12,且当AD=a时,存在两次不同的折叠,使点B落在AC边上两个不同的位置,请直接写出a的取值范围.
每日一题51 答案
解: (1)画图如下:猜想函数的类别为二次函数;
图1
(2)如图1,过点F,D分别作FG,DH垂直于y轴,垂足分别为G,H,则∠FGK=∠DHK=90 .
设FD交y轴于点K,∵D点与F点关于y轴上的K点成中心对称,∴KF=KD,
∵∠FKG=∠DKH,∴Rt△FGK≌Rt△DHK,∴FG=DH.
由yAC=-可知A(0,4) ,又∵B为(-2,0),∴yAB=2x+4,过点F作FR⊥x轴于点R,
∵D点的横坐标为m,∴F(-m,-2m+4),∴ER=2m,FR=-2m+4,
∵EF2=FR2+ER2,∴l=EF2=8m2-16m+16=8(m-1)2+8.
令-=0,解得x=1.5,∴,∴当m=1时,l的最小值为8.∴EF的最小值为2.
(3)分以下三种情形进行讨论:
①∠FBE为定角,不可能为直角;
②当∠BEF=90 ,E点与O点重合,D点与A点、F点重合,此时m=0;
③当∠BFE=90 时,如图2,
由于BF2+EF2=BE2, 由(2)得EF2=8m2﹣16m+16,又∵BR=﹣m+2,FR=﹣2m+4,
∴BF2=BR2+FR2=(﹣m+2)2+(﹣2m+4)2=5m2﹣20m+20,又∵BE2=(m+2)2,
∴(5m2﹣20m+8)+(8m2﹣16m+16)2=(m+2)2,化简得,3m2﹣10m+8=0,解得m1=,m2=2(不符题意,舍去),综上,当△BEF为直角三角形时,m=0或.
每日一题52 答案
解:如图1中,△AFG是等腰三角形.
理由:∵AE平分∠BAC,∴∠1=∠2,∵DF⊥AE,∴∠AHF=∠AHG=90°,
∵AH=AH,∴△AHF≌△AHG,∴AF=AG,∴△AFG是等腰三角形.
(2)证明:如图2中,过点O作OL∥AB交DF于L,则∠AFG=∠OLG.
∵AF=AG,∴∠AFG=∠AGF,∵∠AGF=∠OGL,∴∠OGL=∠OLG,∴OG=OL,
∵OL∥AB,∴△DLO∽△DFB,∴,
∵四边形ABCD是矩形,∴BD=2OD,∴BF=2OL,∴BF=2OG.
(3)解:如图3中,过点D作DK⊥AC于K,则∠DKA=∠CDA=90°,
∵∠DAK=∠CAD,∴△ADK∽△ACD,∴.
∵S1 OG DK,S2 BF AD,又∵BF=2OG,,
∴,设CD=2x,AC=3x,则AD=x,∴.
(4)解:设OG=a,AG=k.
①如图4中,连接EF,当点F在线段AB上时,点G在OA上.
∵AF=AG,BF=2OG,∴AF=AG=k,BF=2a,∴AB=k+2a,AC=2AO=2(k+a),
∴AD2=AC2﹣CD2=[2(k+a)]2﹣(k+2a)2=3k2+4ka,
∵∠ABE=∠DAF=90°,∠BAE=∠ADF,∴△ABE∽△DAF,∴,
∴,∴BE,由题意:102aAD (k+2a),
∴AD2=10ka,即10ka=3k2+4ka,∴k=2a,∴AD=2a,
∴BEa,AB=4a,∴tan∠BAE.
②如图5中,当点F在AB的延长线上时,点G在线段OC上,连接EF.
∵AF=AG,BF=2OG,∴AF=AG=k,BF=2a,∴AB=k﹣2a,AC=2(k﹣a),
∴AD2=AC2﹣CD2=[2(k﹣a)]2﹣(k﹣2a)2=3k2﹣4ka,
∵∠ABE=∠DAF=90°,∠BAE=∠ADF,∴△ABE∽△DAF,
∴,∴,∴BE,
由题意:102aAD (k﹣2a),∴AD2=10ka,即10ka=3k2﹣4ka,∴ka,∴ADa,∴BEa,ABa,∴tan∠BAE,
综上所述,tan∠BAE的值为或.
每日一题53 答案
53.解:(1)∵∠ACD=∠B,∠A=∠A,∴△ADC∽△ACB,∴AD:AC=AC:AB,∴AC2=AD·AB.
(2)∵四边形ABCD是平行四边形,
∴AD=BC,∠A=∠C,又∵∠BFE=∠A,∴∠BFE=∠C,又∵∠FBE=∠CBF,∴△BFE∽△BCF,∴BF2=BE·BC,
∴BC==,∴AD=
(3)如图,分别延长EF,DC相交于点G.∵四边形ABCD是菱形,
∴AB//DC,∠BAC=∠BAD,∴四边形AEGC为平行四边形,
∴AC=EG,CG=AE,∠EAC=∠G,∵∠EDF=∠BAC,
∴∠EDF=∠G,又∵∠DEF=∠GED,∴△EDF∽△EGD,
∴DE2=EF·EG,又∵EG=AC=2EF,∴DE2=2EF2,
∴DE=EF,又∵DG:DF=DE:EF,∴DG=DF=5,∴DC=DG-CG=5-2.
每日一题54 答案
解:【思考】四边形ABDE是平行四边形.
证明:如图,∵△ABC≌△DEF,∴AB=DE,∠BAC=∠EDF,
∴AB∥DE,∴四边形ABDE是平行四边形.
【发现】如图,连接BE交AD于点O,∵四边形ABDE为矩形,∴OA=OD=OB=OE,设AF=x cm,则OA=OE=(x+4),∴OF=OA﹣AF=2﹣x,
在Rt△OFE中,∵OF2+EF2=OE2,∴,
解得:x=,∴AF=cm.
【探究】BD=2OF,
证明:如图,延长OF交AE于点H,纸片DEF绕点O旋转前,四边形ABDE为矩形,∴OA=OB=OE=OD.纸片DEF绕点O旋转后,由旋转的性质可知,OA=OB=OE=OD,
∴∠OBD=∠ODB,∠OAE=∠OEA.∴∠ABD+∠BDE+∠DEA+∠EAB=360°,
∴∠ABD+∠BAE=180°,∴AE∥BD,∴∠OHE=∠ODB,
∵EF平分∠OEH,∴∠OEF=∠HEF.
∵∠EFO=∠EFH=90°,EF=EF, ∴△EFO≌△EFH(ASA),
∴EO=EH,FO=FH,∴∠EHO=∠EOH=∠OBD=∠ODB,
∴△EOH≌△OBD(AAS),∴BD=OH=2OF.
每日一题55 答案
【解答】(1)证明:∵AC=BC,∠C=60°,∴△ABC是等边三角形,∴AC=AB,∠A=60°,由题意,得DB=DP,DA=DB,∴DA=DP,∴△ADP使得等边三角形,
∴AP=AD=AB=AC.
(2)解:∵AC=BC=,∠C=90°,∴AB=12,
∵DH⊥AC,∴DH∥BC,∴△ADH∽△ABC,∴,
∵AD=7,∴,∴DH=,将∠B沿过点D的直线折叠,
情形一:当点B落在线段CH上的点P1处时,如图2﹣1中,
∵AB=12,∴DP1=DB=AB﹣AD=5,∴HP1=,
∴A1=AH+HP1=4,
情形二:当点B落在线段AH上的点P2处时,如图2﹣2中,
同法可证HP2=,∴AP2=AH﹣HP2=3,
综上所述,满足条件的AP的值为4或3.
(3)如图3中,过点C作CH⊥AB于H,过点D作DP⊥AC于P.
∵CA=CB,CH⊥AB,∴AH=HB=6,
∴CH==8,当DB=DP时,设BD=PD=x,则AD=12﹣x,
∵tanA=,∴,∴x=,
∴AD=AB﹣BD=,观察图形可知当6<a<时,存在两次不同的折叠,使点B落在AC边上两个不同的位置.
如图1,在平面直角坐标系中,△ABC的顶点A,C分别是直线 与坐标轴的交点,点B的坐标为(﹣2,0),点D是边AC上的一点,DE⊥BC于点E,点F在边AB上,且D,F两点关于y轴上的某点成中心对称,连结DF,EF.设点D的横坐标为m,EF2为l,请探究:
①线段EF长度是否有最小值;
②△BEF能否成为直角三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
