浙教版九上数学每日一题55-60 拓展、探究应用型问题(含解析)
文档属性
| 名称 | 浙教版九上数学每日一题55-60 拓展、探究应用型问题(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
每日一题56 拓展、探究、应用型问题
班级: 姓名:
56.【感知】如图①,在四边形ABCD中,∠C=∠D=90°,点E在边CD上,∠AEB=90°.求证:.
【探究】如图②,在四边形ABCD中,∠C=∠D=90°,点E在边CD上,当点F在AD延长线上,∠FEG=∠AEB=90°,且,连接BG交CD于点H.求证:BH=GH.
【拓展】如图③,点E在四边形ABCD内,∠AEB+∠DEC=180°,且,过E作EF交AD于点F,使∠EFA=∠AEB,延长FE交BC于点G,求证:BG=CG.
每日一题57 拓展、探究、应用型问题
班级: 姓名:
57.问题提出:
(1)在Rt△ABC中,∠ACB=90°,AC>BC,∠ACB的平分线交AB于点D,过点D分别作DE⊥AC,DF⊥BC,垂足分别E、F,在图1中与线段CE相等的线段是 ;
问题探究:
(2)如图2,AB是半圆O的直径,AB=8,P是上一点,且=2,连接PA,PB,∠APB的平分线交AB于点C,过点C分别作CE⊥AP,CF⊥BP,垂足分别为E、F,求线段CF的长;
问题解决:
如图3,是某公园内“少儿活动中心”的设计示意图,已知⊙O的直径AB=70m,点C在上,且CA=CB.P为AB上一点,连接CP并延长,交于点D,连接AD、BD,过点P分别作PE⊥AD,PF⊥BD,垂足分别为E、F.按设计要求,四边形PEDF内部为室内活动区,阴影部分是户外活动区,圆内其余部分为绿化区.设AP的长为x(m),阴影部分的面积为y(m2) .
①求y关于x之间的函数关系式;
②按照“少儿活动中心”的设计要求,发现当AP的长度为30m时,整体布局比较合理.试求当AP=30m时,室内活动区(四边形PEDF)的面积.
图1 图2 图3
每日一题58 拓展、探究、应用型问题
班级: 姓名:
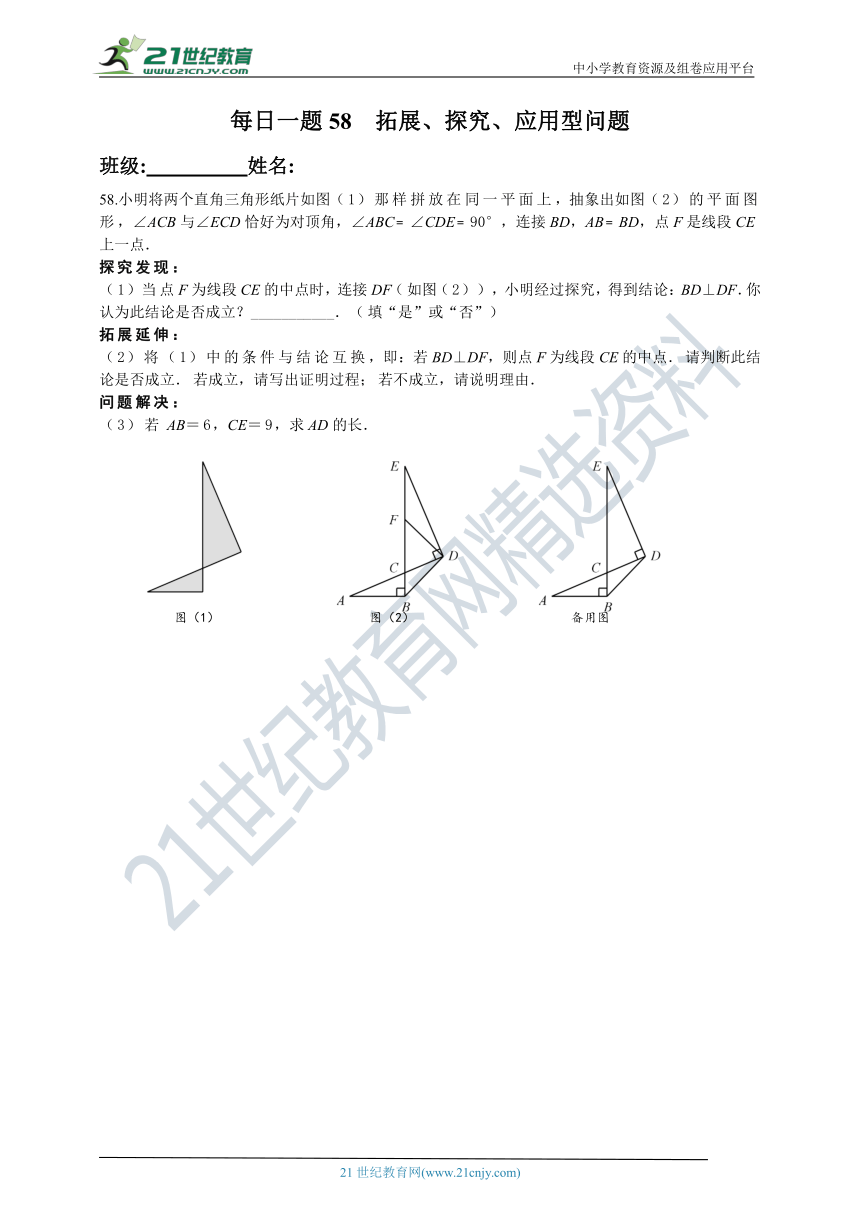
58.小明将两个直角三角形纸片如图(1)那样拼放在同一平面上,抽象出如图(2)的平面图形,∠ACB与∠ECD恰好为对顶角,∠ABC﹦∠CDE﹦90°,连接BD,AB﹦BD,点F是线段CE上一点.
探究发现:
(1)当点F为线段CE的中点时,连接DF(如图(2)),小明经过探究,得到结论:BD⊥DF.你认为此结论是否成立?___________.(填“是”或“否”)
拓展延伸:
(2)将(1)中的条件与结论互换,即:若BD⊥DF,则点F为线段CE的中点.请判断此结论是否成立.若成立,请写出证明过程;若不成立,请说明理由.
问题解决:
(3)若AB=6,CE=9,求AD的长.
每日一题59 拓展、探究、应用型问题
班级: 姓名:
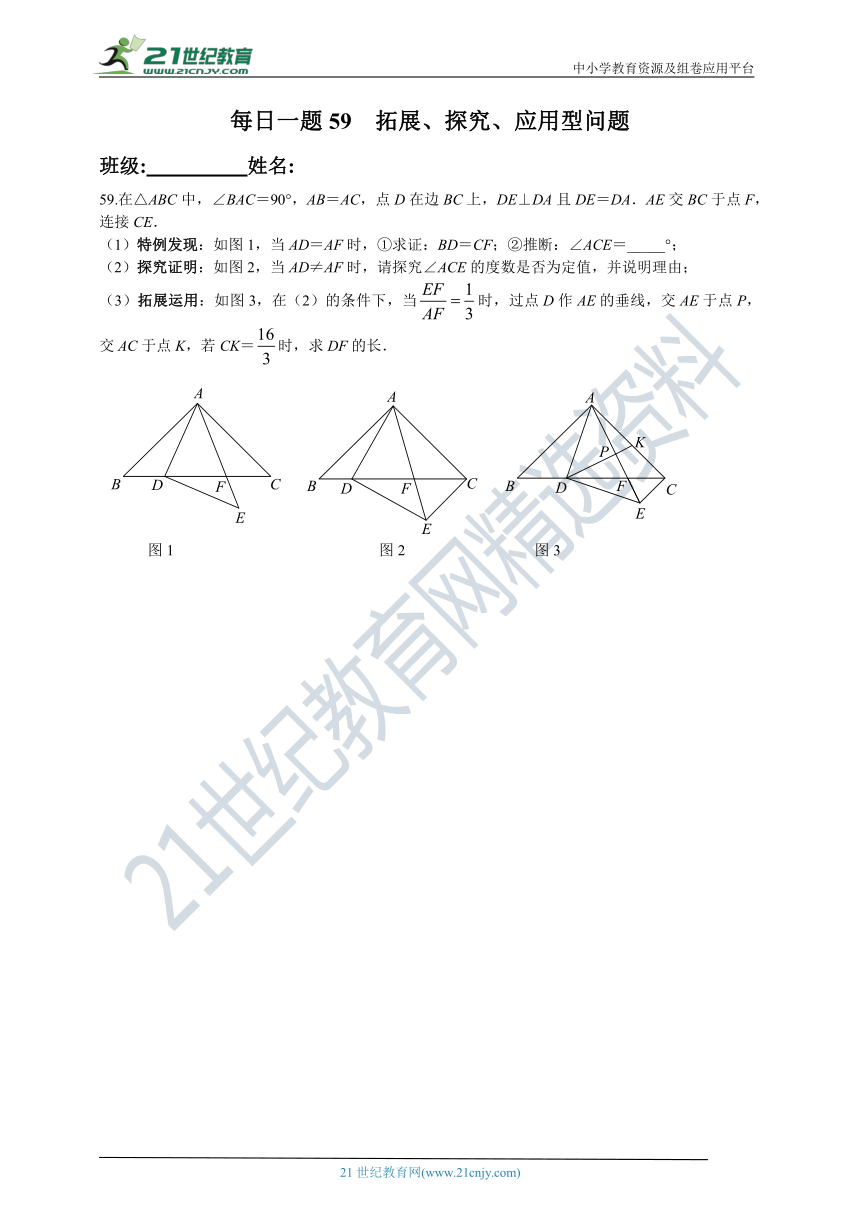
59.在△ABC中,∠BAC=90°,AB=AC,点D在边BC上,DE⊥DA且DE=DA.AE交BC于点F,连接CE.
(1)特例发现:如图1,当AD=AF时,①求证:BD=CF;②推断:∠ACE=_____°;
(2)探究证明:如图2,当AD≠AF时,请探究∠ACE的度数是否为定值,并说明理由;
(3)拓展运用:如图3,在(2)的条件下,当时,过点D作AE的垂线,交AE于点P,交AC于点K,若CK=时,求DF的长.
每日一题60 拓展、探究、应用型问题
班级: 姓名:
60.【学习概念】有一组对角互余的凸四边形称为对余四边形,连接这两个角的顶点的线段称为对余线.
【理解运用】
(1)如图1,对余四边形中,AB=5,BC=6,CD=4,连接AC,若AC=AB,求sin∠CAD的值.
(2)如图2,凸四边形中,AD=BD,AB⊥AC,当2CD2+CB2=CA2时,判断四边形ABCD是否为对余四边形,证明你的结论.
【拓展提升】在平面直角坐标中,A(-1,0),B(3,0),C(1,2),四边形ABCD是对余四边形,点E在对余线BD上,且位于△ABC内部,∠AEC=90°+∠ABC,设 =u,点D的纵坐标为t,请直接写出u与t的函数解析式.
每日一题56 答案
56.证明:(1)∵∠C=∠D=∠AEB=90°,∴∠BEC+∠AED=∠AED+∠EAD=90°.
∴∠BEC=∠EAD.∴Rt△AED∽Rt△EBC.∴ .
(2)如答图1,过点G作GM⊥CD于点M,由(1)可知.
∵,,∴.∴BC=GM.
又∵∠C=∠GMH=90°,∠CHB=∠MHG,∴△BCH≌△GMH.∴BH=GH.
(3)如答图2,在EG上取点M,使∠BME=∠AEB,过点C作CN∥BM,交EG的延长线于点N,则∠N=∠BMG.
∵∠EAF+∠AFE+∠AEF=∠AEF+∠AEB+∠BEM=180°,∠EFA=∠AEB,
∴∠EAF=∠BEM.∴△AEF∽△EBM.∴.
∵∠AEB+∠DEC=180°,∠FEA+∠DFE=180°,而∠EFA=∠AEB,∴∠CED=∠EFD.
∵∠BMG+∠BME=180°,∴∠N=∠EFD.
∵∠EFD+∠EDF+∠FED=∠FED+∠DEC+∠CEN=180°,∴∠EDF=∠CEN.
∴△DEF∽△ECN.∴.又∵,∴,
∴BM=CN.又∵∠N=∠BMG,∠BGM=∠CGN,∴△BGM≌△CGN.∴BG=CG.
每日一题57 答案
57.解:(1)ED、DF、CF;
(2)∵AB是直径,=2,∴∠AOP=90°,∠B=30°.
由题意可知,矩形PECF为正方形.在Rt△APB中,PB=AB·cos30°=4,AP=AB=4.
在Rt△ACE中,CE=AE.设CF=a,由(1)可知:CF=CE=PE=a,则AE=4-a,由CE=AE,可列方程,解得a=,即CF的长为.
(3)如答图,①∵AB为直径,∴∠ACB=∠ADB=90°.
∵AC=BC,∴∠ADC=∠BDC,∴PE=PF.∴四边形PEDF为正方形.
∴∠APE+∠BPF=90°,∠PEA=∠PFB=90°.∴将△APE绕点P逆时针旋转90°,得到△GPF,PA=PG,则G、F、B三点共线,△PBG为直角三角形,∠BPG=90°.
∴.
在Rt△ABC中,AC=BC=35,∴=AC2=1225.
∴y=+1225=.
②当x=30时,PG=30,PB=40.在Rt△PGB中,BG=50.
运用等积法,有×30×40=PB·PF∴PF=24.∴正方形PEDF的面积=PF2=242=576(m2).
∴当AP=30m时,室内活动区(四边形PEDF)的面积为576m2.
每日一题58 答案
58.(1)是;
(2)结论成立. 理由如下:
∵BD⊥DF,ED⊥AD, ∴∠BDC+∠CDF﹦90°,∠EDF+∠CDF﹦90°.
∴∠BDC﹦∠EDF.
∵AB﹦BD,∴∠A﹦∠BDC.∴∠A﹦∠EDF.
又∵∠A﹦∠E,∴∠E﹦∠EDF.∴EF﹦FD.
又∠E+∠ECD﹦90°,∴∠ECD﹦∠CDF.∴CF﹦DF.∴CF﹦EF.∴F为CE的中点.
(3)在备用图中,设G为EC的中点,则DG⊥BD.
∴GD﹦EC﹦. 又BD=AB=6,
在Rt△GDB中,GB= EQ \r(62+()2) =. ∴CB=—=3.
在Rt△ABC中,AC==3.
由条件得:△ABC∽△EDC. ∴ EQ \f(3,9) =.∴CD= EQ \f(9,5) .
∴AD=AC+CD=3+ EQ \f(9,5) ﹦ EQ \f(24,5) .
每日一题59 答案
59.解:(1)①证明:如答图1,过点A作AM⊥BC于点M.
∵AB=AC,AD=AF,AM⊥BC,
∴BM=CM,DM=FM.
∴BM-DM=CM-FM,即BD=CF.
②90(证明△ABD≌△DCE,可得∠DCE=∠B=45°).
(2)∠ACE=90°,理由如下:如答图2,过点A作AM⊥BC于点M,点E作EN⊥BC于点N.
∵AM⊥BC,EN⊥BC,DE⊥DA,
∴∠AMD=∠DNE=90°,∠DAM+∠ADM=∠ADM+∠EDN=90°.
∴∠DAM=∠EDN.
又∵DE=DA,∴△AMD≌△DNE.∴AM=DN=CM,DM=EN.
∴DM=CN.∴CN=EN.∴∠ECN=∠ACN=45°.∴∠ACE=90°.
(3)如答图3,过点A作AM⊥BC于点M,点E作EN⊥BC于点N,连接KE.由(2)可知DM=NF=CN=k,由AM∥EN,得△AMF∽△ENF,从而,于是AM=CM=DN=3k,MF=k,NF=k,故DF=k.
∵DA=DE,DP⊥AE,∴直线DK垂直平分线段AE,于是KE=AK=.
∵CE=k,
∴在Rt△CEK中,由勾股定理,得,解得k=2.
∴DF=k=5.
每日一题60 答案
60.解:(1) ∵四边形ABCD为对余四边形,所以∠B+∠D=90°,过点A作AE⊥BC,
∵AC=AB,∴BE=CE=3.在Rt△AEB中,.
过点C作CF⊥AD,∴∠D+∠DCF=90°,∴∠B=∠DCF
∴△AEB∽△DFC,∴,∴,∴,∴sin∠CAD=.
(2)∵四边形ABCD中,AB=AC,AB⊥AC,∴∠DAB=∠DBA=45°,
过点D作DM⊥CD,使CD=CM,连接CM,∴∠DMC=∠DCM=45°,
∵∠ADB=∠CDM=90°,∴∠ADB+∠BDC=∠CDM+∠BDC, ∴∠ADC=∠BDM
在△ADC与△BDM中, ∴△ADC≌△BDM
在△MDC中,CM2=CD2+DM2=2CD2, ∵2CD2+CB2=CA2 ∴CM2+CB2=BM2,
∴△BCM为直角三角形,∴∠BCM=90°.∴∠DCM=45°,∴∠DCB=∠BCM-∠DCM=45°,
∴∠DCB+∠DAB=90° ∴从而证明四边形ABCD为对余四边形.
(3)先证得∠AEC=135°,得出AECD四点共圆,假设圆心为F,连接FA,FA⊥x轴,过点D作DG⊥AF于G,过点D作DH⊥x轴于点H,先根据弦切角证得∠BAE=∠BDA,可得出△ABE∽△DBA,得出u===,∵∴DH=t ∴AG=t ∵FA=2∴FG=2—t∴ ∵∴∴∴
第56题图① 第56题图② 第56题图③
图(1) 图(2) 备用图
图1 图2 图3
A
B
C
D
D
A
B
C
第56题答图1
第27题答图2
第24题答图1
第24题答图2
第24题答图3
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
每日一题56 拓展、探究、应用型问题
班级: 姓名:
56.【感知】如图①,在四边形ABCD中,∠C=∠D=90°,点E在边CD上,∠AEB=90°.求证:.
【探究】如图②,在四边形ABCD中,∠C=∠D=90°,点E在边CD上,当点F在AD延长线上,∠FEG=∠AEB=90°,且,连接BG交CD于点H.求证:BH=GH.
【拓展】如图③,点E在四边形ABCD内,∠AEB+∠DEC=180°,且,过E作EF交AD于点F,使∠EFA=∠AEB,延长FE交BC于点G,求证:BG=CG.
每日一题57 拓展、探究、应用型问题
班级: 姓名:
57.问题提出:
(1)在Rt△ABC中,∠ACB=90°,AC>BC,∠ACB的平分线交AB于点D,过点D分别作DE⊥AC,DF⊥BC,垂足分别E、F,在图1中与线段CE相等的线段是 ;
问题探究:
(2)如图2,AB是半圆O的直径,AB=8,P是上一点,且=2,连接PA,PB,∠APB的平分线交AB于点C,过点C分别作CE⊥AP,CF⊥BP,垂足分别为E、F,求线段CF的长;
问题解决:
如图3,是某公园内“少儿活动中心”的设计示意图,已知⊙O的直径AB=70m,点C在上,且CA=CB.P为AB上一点,连接CP并延长,交于点D,连接AD、BD,过点P分别作PE⊥AD,PF⊥BD,垂足分别为E、F.按设计要求,四边形PEDF内部为室内活动区,阴影部分是户外活动区,圆内其余部分为绿化区.设AP的长为x(m),阴影部分的面积为y(m2) .
①求y关于x之间的函数关系式;
②按照“少儿活动中心”的设计要求,发现当AP的长度为30m时,整体布局比较合理.试求当AP=30m时,室内活动区(四边形PEDF)的面积.
图1 图2 图3
每日一题58 拓展、探究、应用型问题
班级: 姓名:
58.小明将两个直角三角形纸片如图(1)那样拼放在同一平面上,抽象出如图(2)的平面图形,∠ACB与∠ECD恰好为对顶角,∠ABC﹦∠CDE﹦90°,连接BD,AB﹦BD,点F是线段CE上一点.
探究发现:
(1)当点F为线段CE的中点时,连接DF(如图(2)),小明经过探究,得到结论:BD⊥DF.你认为此结论是否成立?___________.(填“是”或“否”)
拓展延伸:
(2)将(1)中的条件与结论互换,即:若BD⊥DF,则点F为线段CE的中点.请判断此结论是否成立.若成立,请写出证明过程;若不成立,请说明理由.
问题解决:
(3)若AB=6,CE=9,求AD的长.
每日一题59 拓展、探究、应用型问题
班级: 姓名:
59.在△ABC中,∠BAC=90°,AB=AC,点D在边BC上,DE⊥DA且DE=DA.AE交BC于点F,连接CE.
(1)特例发现:如图1,当AD=AF时,①求证:BD=CF;②推断:∠ACE=_____°;
(2)探究证明:如图2,当AD≠AF时,请探究∠ACE的度数是否为定值,并说明理由;
(3)拓展运用:如图3,在(2)的条件下,当时,过点D作AE的垂线,交AE于点P,交AC于点K,若CK=时,求DF的长.
每日一题60 拓展、探究、应用型问题
班级: 姓名:
60.【学习概念】有一组对角互余的凸四边形称为对余四边形,连接这两个角的顶点的线段称为对余线.
【理解运用】
(1)如图1,对余四边形中,AB=5,BC=6,CD=4,连接AC,若AC=AB,求sin∠CAD的值.
(2)如图2,凸四边形中,AD=BD,AB⊥AC,当2CD2+CB2=CA2时,判断四边形ABCD是否为对余四边形,证明你的结论.
【拓展提升】在平面直角坐标中,A(-1,0),B(3,0),C(1,2),四边形ABCD是对余四边形,点E在对余线BD上,且位于△ABC内部,∠AEC=90°+∠ABC,设 =u,点D的纵坐标为t,请直接写出u与t的函数解析式.
每日一题56 答案
56.证明:(1)∵∠C=∠D=∠AEB=90°,∴∠BEC+∠AED=∠AED+∠EAD=90°.
∴∠BEC=∠EAD.∴Rt△AED∽Rt△EBC.∴ .
(2)如答图1,过点G作GM⊥CD于点M,由(1)可知.
∵,,∴.∴BC=GM.
又∵∠C=∠GMH=90°,∠CHB=∠MHG,∴△BCH≌△GMH.∴BH=GH.
(3)如答图2,在EG上取点M,使∠BME=∠AEB,过点C作CN∥BM,交EG的延长线于点N,则∠N=∠BMG.
∵∠EAF+∠AFE+∠AEF=∠AEF+∠AEB+∠BEM=180°,∠EFA=∠AEB,
∴∠EAF=∠BEM.∴△AEF∽△EBM.∴.
∵∠AEB+∠DEC=180°,∠FEA+∠DFE=180°,而∠EFA=∠AEB,∴∠CED=∠EFD.
∵∠BMG+∠BME=180°,∴∠N=∠EFD.
∵∠EFD+∠EDF+∠FED=∠FED+∠DEC+∠CEN=180°,∴∠EDF=∠CEN.
∴△DEF∽△ECN.∴.又∵,∴,
∴BM=CN.又∵∠N=∠BMG,∠BGM=∠CGN,∴△BGM≌△CGN.∴BG=CG.
每日一题57 答案
57.解:(1)ED、DF、CF;
(2)∵AB是直径,=2,∴∠AOP=90°,∠B=30°.
由题意可知,矩形PECF为正方形.在Rt△APB中,PB=AB·cos30°=4,AP=AB=4.
在Rt△ACE中,CE=AE.设CF=a,由(1)可知:CF=CE=PE=a,则AE=4-a,由CE=AE,可列方程,解得a=,即CF的长为.
(3)如答图,①∵AB为直径,∴∠ACB=∠ADB=90°.
∵AC=BC,∴∠ADC=∠BDC,∴PE=PF.∴四边形PEDF为正方形.
∴∠APE+∠BPF=90°,∠PEA=∠PFB=90°.∴将△APE绕点P逆时针旋转90°,得到△GPF,PA=PG,则G、F、B三点共线,△PBG为直角三角形,∠BPG=90°.
∴.
在Rt△ABC中,AC=BC=35,∴=AC2=1225.
∴y=+1225=.
②当x=30时,PG=30,PB=40.在Rt△PGB中,BG=50.
运用等积法,有×30×40=PB·PF∴PF=24.∴正方形PEDF的面积=PF2=242=576(m2).
∴当AP=30m时,室内活动区(四边形PEDF)的面积为576m2.
每日一题58 答案
58.(1)是;
(2)结论成立. 理由如下:
∵BD⊥DF,ED⊥AD, ∴∠BDC+∠CDF﹦90°,∠EDF+∠CDF﹦90°.
∴∠BDC﹦∠EDF.
∵AB﹦BD,∴∠A﹦∠BDC.∴∠A﹦∠EDF.
又∵∠A﹦∠E,∴∠E﹦∠EDF.∴EF﹦FD.
又∠E+∠ECD﹦90°,∴∠ECD﹦∠CDF.∴CF﹦DF.∴CF﹦EF.∴F为CE的中点.
(3)在备用图中,设G为EC的中点,则DG⊥BD.
∴GD﹦EC﹦. 又BD=AB=6,
在Rt△GDB中,GB= EQ \r(62+()2) =. ∴CB=—=3.
在Rt△ABC中,AC==3.
由条件得:△ABC∽△EDC. ∴ EQ \f(3,9) =.∴CD= EQ \f(9,5) .
∴AD=AC+CD=3+ EQ \f(9,5) ﹦ EQ \f(24,5) .
每日一题59 答案
59.解:(1)①证明:如答图1,过点A作AM⊥BC于点M.
∵AB=AC,AD=AF,AM⊥BC,
∴BM=CM,DM=FM.
∴BM-DM=CM-FM,即BD=CF.
②90(证明△ABD≌△DCE,可得∠DCE=∠B=45°).
(2)∠ACE=90°,理由如下:如答图2,过点A作AM⊥BC于点M,点E作EN⊥BC于点N.
∵AM⊥BC,EN⊥BC,DE⊥DA,
∴∠AMD=∠DNE=90°,∠DAM+∠ADM=∠ADM+∠EDN=90°.
∴∠DAM=∠EDN.
又∵DE=DA,∴△AMD≌△DNE.∴AM=DN=CM,DM=EN.
∴DM=CN.∴CN=EN.∴∠ECN=∠ACN=45°.∴∠ACE=90°.
(3)如答图3,过点A作AM⊥BC于点M,点E作EN⊥BC于点N,连接KE.由(2)可知DM=NF=CN=k,由AM∥EN,得△AMF∽△ENF,从而,于是AM=CM=DN=3k,MF=k,NF=k,故DF=k.
∵DA=DE,DP⊥AE,∴直线DK垂直平分线段AE,于是KE=AK=.
∵CE=k,
∴在Rt△CEK中,由勾股定理,得,解得k=2.
∴DF=k=5.
每日一题60 答案
60.解:(1) ∵四边形ABCD为对余四边形,所以∠B+∠D=90°,过点A作AE⊥BC,
∵AC=AB,∴BE=CE=3.在Rt△AEB中,.
过点C作CF⊥AD,∴∠D+∠DCF=90°,∴∠B=∠DCF
∴△AEB∽△DFC,∴,∴,∴,∴sin∠CAD=.
(2)∵四边形ABCD中,AB=AC,AB⊥AC,∴∠DAB=∠DBA=45°,
过点D作DM⊥CD,使CD=CM,连接CM,∴∠DMC=∠DCM=45°,
∵∠ADB=∠CDM=90°,∴∠ADB+∠BDC=∠CDM+∠BDC, ∴∠ADC=∠BDM
在△ADC与△BDM中, ∴△ADC≌△BDM
在△MDC中,CM2=CD2+DM2=2CD2, ∵2CD2+CB2=CA2 ∴CM2+CB2=BM2,
∴△BCM为直角三角形,∴∠BCM=90°.∴∠DCM=45°,∴∠DCB=∠BCM-∠DCM=45°,
∴∠DCB+∠DAB=90° ∴从而证明四边形ABCD为对余四边形.
(3)先证得∠AEC=135°,得出AECD四点共圆,假设圆心为F,连接FA,FA⊥x轴,过点D作DG⊥AF于G,过点D作DH⊥x轴于点H,先根据弦切角证得∠BAE=∠BDA,可得出△ABE∽△DBA,得出u===,∵∴DH=t ∴AG=t ∵FA=2∴FG=2—t∴ ∵∴∴∴
第56题图① 第56题图② 第56题图③
图(1) 图(2) 备用图
图1 图2 图3
A
B
C
D
D
A
B
C
第56题答图1
第27题答图2
第24题答图1
第24题答图2
第24题答图3
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
