浙教版八下数学每日一题61-65 反比例函数填选压轴题(含解析)
文档属性
| 名称 | 浙教版八下数学每日一题61-65 反比例函数填选压轴题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 11:17:27 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
每日一题61 反比例函数填选压轴题
班级: 姓名:
61-1.如图,在平面直角坐标系中,直线y=-x与双曲线y=交于A、B两点,P是以点C(2,2)为圆心,半径长1的圆上一动点,连接AP,Q为AP的中点.若线段OQ长度的最大值为2,则k的值为( )
A.- B.- C.-2 D.-
61-2.如图,一次函数y=x+k(k>0)的图象与x轴和y轴分别交于点A和点B,与反比例函数y=的图象在第一象限内交于点C,CD⊥x轴,CE⊥y轴,垂足分别为点D,E.当矩形ODCE与△ OAB的面积相等时,k的值为 .
每日一题62 反比例函数填选压轴题
班级: 姓名:
62-1.如图在平面直角坐标系中,矩形ABCD的顶点A,C分别在x轴,y轴的正半轴上,点D(-2,3),AD=5,若反比例函数的图像经过点B,则k的值为( )
A. B.8 C.10 D.
62-2.如图,点A在反比例函数(k>0)的图像上,点B在x轴的负半轴上,直线AB交y轴于点C.若,△AOB的面积为5,则k的值为 .
每日一题63 反比例函数填选压轴题
班级: 姓名:
63-1.如图,点D是平行四边形OABC内一点,CD与x轴平行,BD与y轴平行,BD=,∠ADB=135°,S△ABD=2.若反比例函数y=(x>0)的图像经过A、D两点,则k的值是( )
A.2 B.4 C.3 D.6
INCLUDEPICTURE"20CZSX4.TIF" INCLUDEPICTURE "C:\\Users\\chenxi\\Desktop\\20CZSX4.TIF" \* MERGEFORMATINET INCLUDEPICTURE "C:\\Users\\余中华\\Desktop\\20CZSX4.TIF" \* MERGEFORMATINET INCLUDEPICTURE "C:\\Users\\鱼\\Desktop\\20CZSX4.TIF" \* MERGEFORMATINET
63-2 .如图,在平面直角坐标系xOy中,一次函数y=x+1的图象与反比例函数y=的图象交于A,B两点,若点P是第一象限内反比例函数图象上一点,且△ABP的面积是△AOB的面积的2倍,则点P的横坐标为_______.
每日一题64 反比例函数填选压轴题
班级: 姓名:
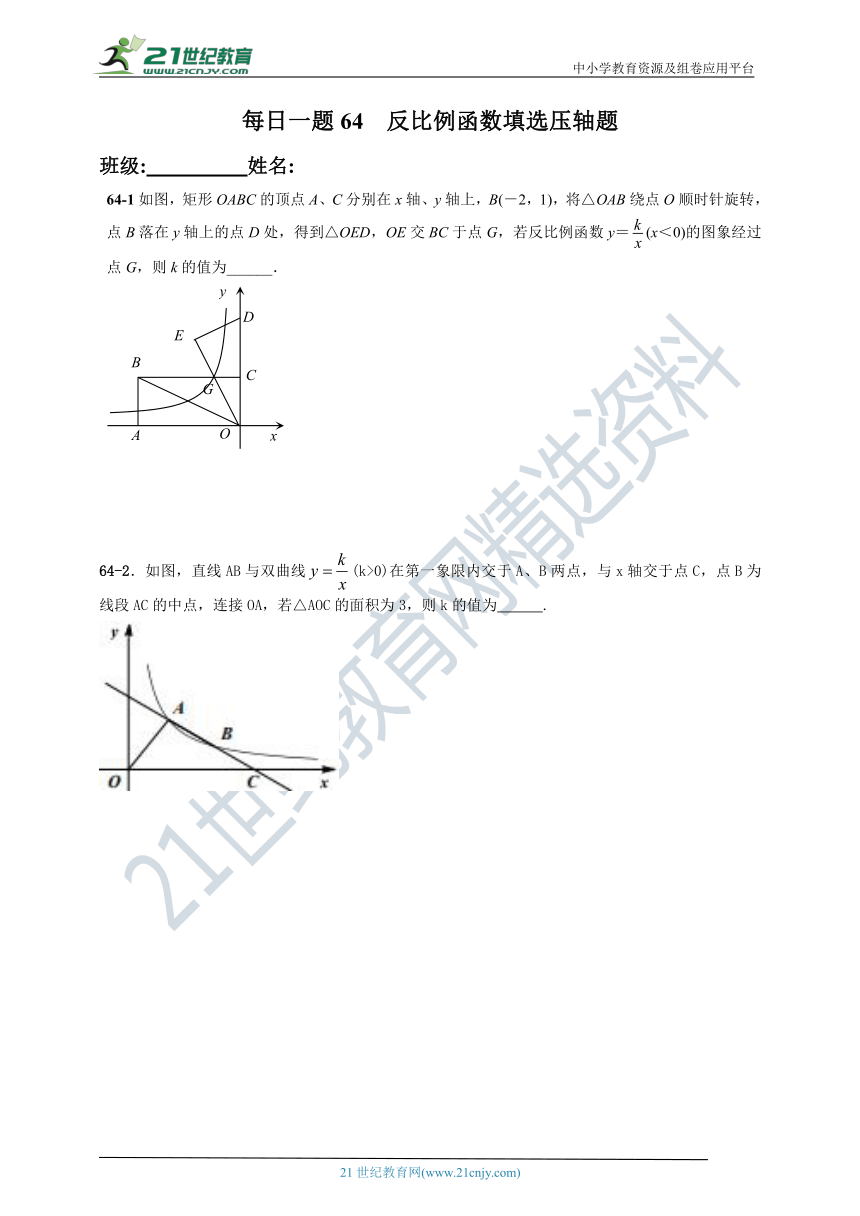
64-1如图,矩形OABC的顶点A、C分别在x轴、y轴上,B(-2,1),将△OAB绕点O顺时针旋转,点B落在y轴上的点D处,得到△OED,OE交BC于点G,若反比例函数y=(x<0)的图象经过点G,则k的值为______.
64-2.如图,直线AB与双曲线(k>0)在第一象限内交于A、B两点,与x轴交于点C,点B为线段AC的中点,连接OA,若△AOC的面积为3,则k的值为 .
每日一题65 反比例函数填选压轴题
班级: 姓名:
65-1如图,曲线是双曲线:(x>0)绕原点O逆时针旋转45°得到的图形,P是曲线上任意一点,点A在直线l:上,且PA=PO,则△POA的面积等于( ).
A. B.6 C.3 D.12
65-2.如图,在△ABC中,AB=AC,点A在反比例函数(k>0,x>0)的图象上,点B,C在x轴上,OC=OB,延长AC交y轴于点D,连接BD,若△BCD的面积等于1,则k的值为 .
每日一题61 答案
61.1{答案}A {解析}连接BP,得到OQ是△ABP的中位线,当P、C、B三点共线时PB长度最大,PB=2OQ=4,设点B的坐标为(x,-x),根据点 C(2,2),可利用勾股定理求出点B的坐标,代入反比例函数关系式即可求出k的值.∵直线y=-x与双曲线y=的图形均关于直线y=x对称,∴OA=OB,∵点Q是AP的中点,点O是AB的中点,∴OQ是△ABP的中位线,当OQ的长度最大时,即PB的长度最大;∵PB≤PC+BC,当三点共线时PB长度最大,∴当P、C、B三点共线时PB=2OQ=4;∵PC=1,∴BC=3;设点B的坐标为(x,-x),则BC==3,解得x= EQ \F(,2)或x=- EQ \F(,2)(舍去),故B ( EQ \F(,2),- EQ \F(,2)),代入y=中可得k=-.
61-2.{答案}2{解析}在一次函数y=x+k中,当x=0时,则y=k,即OB=k;当y=0时,x=-k,即OA=k,故S△AOB=k2.结合反比例函数的几何意义,得S矩形=k.由S矩形=S△AOB,得:k2=k,解得:k=2或k=0(舍去).
每日一题62 答案
62-1 {答案}D {解析}本题考查了点的坐标,矩形的性质,相似三角形的判定和性质,用待定系数法求反比例函数的表达式.如图,过点B作BE⊥x轴于E,过点D作DF⊥x轴于点F,∴∠AFD=∠AEB=90°.∵四边形ABCD是矩形,∴∠ADC=∠DAB=90°,AB=CD.∵D(-2,3),∴OF=2,DF=3.在Rt△ADF中,AD=5,∴AF==4,∴AO=4-2=2.设AD与x轴交于点G,∵AD∥OC,∴△AOG∽△AFD,∴,∴OG=,AG=,∴DG=5-=.∵∠AOG=∠CDG=90°,∠AGO=∠CGD=90°,∴△AGO∽△CGD,∴,∴CD=,∴AB=.∵∠DAB=∠AEB=90°,∴∠DAF+∠BAE=90°,∠BAE+∠ABE=90°,∴∠DAF=∠ABE,∴△ADF∽BAE,∴,解得AE=2,BE=,∴OE=2+2=4,∴点B(4,),∴k=4×=. 因此本题选D.
62-2{答案}5{解析}如答图,过点A作AD⊥y轴于点D,则△ADC∽△BOC,从而.∵,△AOB的面积为5,∴S△AOC=S△AOB=.∴S△ACD=S△AOC=.∴S△AOD=S△ADC+S△AOC=.∵点A在反比例函数(k>0)的图像上,AD⊥y轴,∴k=.∴k=5.故答案为5.
每日一题63 答案
63-1{答案}D {解析}{解析}过点D、点A分别作x轴、y轴的垂线,两条垂线相交于点E,过点A作AF⊥x轴于点F,由∠BDF=135°,可证△DEA为等腰直角三角形,因为S△ABD=BD·AE,2=×·AE,所以AE=2,所以DE=AE=2,又由于BC与OA平行且相等,可证△CDB≌△OAF,所以AF=,设A(,),所以D(-2,3),所以(-2)×3=k,解得k=6.
63-2 {答案}2或
每日一题64 答案
64-1{答案}- {解析}由点B的坐标可知OC=AB=1,OA=2.由旋转可知△OED≌△OAB,∴∠E=∠OAB=90°,ED=AB=1,OE=OA=2.由△OCG∽△OED,得=,即=.∴CG=,点G的坐标为(-,1).∴k=-×1=-.
62-2{答案}2 {解析}本题考查了反比例函数有关的面积计算问题、线段中点的坐标公式、三角形的面积公式,解答过程如下:
作AD⊥x轴于D,设点A的坐标为(a,b),则AD=b,ab=k.
∵点B为线段AC的中点,点C在x轴上,∴点B的纵坐标为.
∵点A、B都在,∴点B的横坐标为2a,点C的横坐标为3a,∴OC=3a.
∵,∴,即k=3.
每日一题65 答案
65-1. 【答案】B 解析:如下图,将点△AOP绕点O按顺时针旋转45°,得到△A'OP',则点A'在x轴上,点P'在双曲线上,作P'B⊥x轴于点B,易得,所以 故答案为B.
65-2.{答案}3{解析}本题可结合等腰三角形的三线合一,相似三角形的性质及反比例函数k的几何意义求解. 过点A作AH⊥x轴于H,连接AO.∵AB=AC,AH⊥x轴,∴CH=BH,∵OCOB,∴OC=CH.∵∠OCD=∠ACH,∠COD=∠AHC=90°,∴△OCD∽△HCA,∴==.∴==,∴ S△ACB=2.∵CH=BH,∴S△ACH=S△ACB=1.∵OC=CH,∴S△AOC=S△ACH=,∴S△AOH=S△AOC+S△ACH=,∴ =,解得k=3.
x
O
y
G
D
E
C
A
B
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
每日一题61 反比例函数填选压轴题
班级: 姓名:
61-1.如图,在平面直角坐标系中,直线y=-x与双曲线y=交于A、B两点,P是以点C(2,2)为圆心,半径长1的圆上一动点,连接AP,Q为AP的中点.若线段OQ长度的最大值为2,则k的值为( )
A.- B.- C.-2 D.-
61-2.如图,一次函数y=x+k(k>0)的图象与x轴和y轴分别交于点A和点B,与反比例函数y=的图象在第一象限内交于点C,CD⊥x轴,CE⊥y轴,垂足分别为点D,E.当矩形ODCE与△ OAB的面积相等时,k的值为 .
每日一题62 反比例函数填选压轴题
班级: 姓名:
62-1.如图在平面直角坐标系中,矩形ABCD的顶点A,C分别在x轴,y轴的正半轴上,点D(-2,3),AD=5,若反比例函数的图像经过点B,则k的值为( )
A. B.8 C.10 D.
62-2.如图,点A在反比例函数(k>0)的图像上,点B在x轴的负半轴上,直线AB交y轴于点C.若,△AOB的面积为5,则k的值为 .
每日一题63 反比例函数填选压轴题
班级: 姓名:
63-1.如图,点D是平行四边形OABC内一点,CD与x轴平行,BD与y轴平行,BD=,∠ADB=135°,S△ABD=2.若反比例函数y=(x>0)的图像经过A、D两点,则k的值是( )
A.2 B.4 C.3 D.6
INCLUDEPICTURE"20CZSX4.TIF" INCLUDEPICTURE "C:\\Users\\chenxi\\Desktop\\20CZSX4.TIF" \* MERGEFORMATINET INCLUDEPICTURE "C:\\Users\\余中华\\Desktop\\20CZSX4.TIF" \* MERGEFORMATINET INCLUDEPICTURE "C:\\Users\\鱼\\Desktop\\20CZSX4.TIF" \* MERGEFORMATINET
63-2 .如图,在平面直角坐标系xOy中,一次函数y=x+1的图象与反比例函数y=的图象交于A,B两点,若点P是第一象限内反比例函数图象上一点,且△ABP的面积是△AOB的面积的2倍,则点P的横坐标为_______.
每日一题64 反比例函数填选压轴题
班级: 姓名:
64-1如图,矩形OABC的顶点A、C分别在x轴、y轴上,B(-2,1),将△OAB绕点O顺时针旋转,点B落在y轴上的点D处,得到△OED,OE交BC于点G,若反比例函数y=(x<0)的图象经过点G,则k的值为______.
64-2.如图,直线AB与双曲线(k>0)在第一象限内交于A、B两点,与x轴交于点C,点B为线段AC的中点,连接OA,若△AOC的面积为3,则k的值为 .
每日一题65 反比例函数填选压轴题
班级: 姓名:
65-1如图,曲线是双曲线:(x>0)绕原点O逆时针旋转45°得到的图形,P是曲线上任意一点,点A在直线l:上,且PA=PO,则△POA的面积等于( ).
A. B.6 C.3 D.12
65-2.如图,在△ABC中,AB=AC,点A在反比例函数(k>0,x>0)的图象上,点B,C在x轴上,OC=OB,延长AC交y轴于点D,连接BD,若△BCD的面积等于1,则k的值为 .
每日一题61 答案
61.1{答案}A {解析}连接BP,得到OQ是△ABP的中位线,当P、C、B三点共线时PB长度最大,PB=2OQ=4,设点B的坐标为(x,-x),根据点 C(2,2),可利用勾股定理求出点B的坐标,代入反比例函数关系式即可求出k的值.∵直线y=-x与双曲线y=的图形均关于直线y=x对称,∴OA=OB,∵点Q是AP的中点,点O是AB的中点,∴OQ是△ABP的中位线,当OQ的长度最大时,即PB的长度最大;∵PB≤PC+BC,当三点共线时PB长度最大,∴当P、C、B三点共线时PB=2OQ=4;∵PC=1,∴BC=3;设点B的坐标为(x,-x),则BC==3,解得x= EQ \F(,2)或x=- EQ \F(,2)(舍去),故B ( EQ \F(,2),- EQ \F(,2)),代入y=中可得k=-.
61-2.{答案}2{解析}在一次函数y=x+k中,当x=0时,则y=k,即OB=k;当y=0时,x=-k,即OA=k,故S△AOB=k2.结合反比例函数的几何意义,得S矩形=k.由S矩形=S△AOB,得:k2=k,解得:k=2或k=0(舍去).
每日一题62 答案
62-1 {答案}D {解析}本题考查了点的坐标,矩形的性质,相似三角形的判定和性质,用待定系数法求反比例函数的表达式.如图,过点B作BE⊥x轴于E,过点D作DF⊥x轴于点F,∴∠AFD=∠AEB=90°.∵四边形ABCD是矩形,∴∠ADC=∠DAB=90°,AB=CD.∵D(-2,3),∴OF=2,DF=3.在Rt△ADF中,AD=5,∴AF==4,∴AO=4-2=2.设AD与x轴交于点G,∵AD∥OC,∴△AOG∽△AFD,∴,∴OG=,AG=,∴DG=5-=.∵∠AOG=∠CDG=90°,∠AGO=∠CGD=90°,∴△AGO∽△CGD,∴,∴CD=,∴AB=.∵∠DAB=∠AEB=90°,∴∠DAF+∠BAE=90°,∠BAE+∠ABE=90°,∴∠DAF=∠ABE,∴△ADF∽BAE,∴,解得AE=2,BE=,∴OE=2+2=4,∴点B(4,),∴k=4×=. 因此本题选D.
62-2{答案}5{解析}如答图,过点A作AD⊥y轴于点D,则△ADC∽△BOC,从而.∵,△AOB的面积为5,∴S△AOC=S△AOB=.∴S△ACD=S△AOC=.∴S△AOD=S△ADC+S△AOC=.∵点A在反比例函数(k>0)的图像上,AD⊥y轴,∴k=.∴k=5.故答案为5.
每日一题63 答案
63-1{答案}D {解析}{解析}过点D、点A分别作x轴、y轴的垂线,两条垂线相交于点E,过点A作AF⊥x轴于点F,由∠BDF=135°,可证△DEA为等腰直角三角形,因为S△ABD=BD·AE,2=×·AE,所以AE=2,所以DE=AE=2,又由于BC与OA平行且相等,可证△CDB≌△OAF,所以AF=,设A(,),所以D(-2,3),所以(-2)×3=k,解得k=6.
63-2 {答案}2或
每日一题64 答案
64-1{答案}- {解析}由点B的坐标可知OC=AB=1,OA=2.由旋转可知△OED≌△OAB,∴∠E=∠OAB=90°,ED=AB=1,OE=OA=2.由△OCG∽△OED,得=,即=.∴CG=,点G的坐标为(-,1).∴k=-×1=-.
62-2{答案}2 {解析}本题考查了反比例函数有关的面积计算问题、线段中点的坐标公式、三角形的面积公式,解答过程如下:
作AD⊥x轴于D,设点A的坐标为(a,b),则AD=b,ab=k.
∵点B为线段AC的中点,点C在x轴上,∴点B的纵坐标为.
∵点A、B都在,∴点B的横坐标为2a,点C的横坐标为3a,∴OC=3a.
∵,∴,即k=3.
每日一题65 答案
65-1. 【答案】B 解析:如下图,将点△AOP绕点O按顺时针旋转45°,得到△A'OP',则点A'在x轴上,点P'在双曲线上,作P'B⊥x轴于点B,易得,所以 故答案为B.
65-2.{答案}3{解析}本题可结合等腰三角形的三线合一,相似三角形的性质及反比例函数k的几何意义求解. 过点A作AH⊥x轴于H,连接AO.∵AB=AC,AH⊥x轴,∴CH=BH,∵OCOB,∴OC=CH.∵∠OCD=∠ACH,∠COD=∠AHC=90°,∴△OCD∽△HCA,∴==.∴==,∴ S△ACB=2.∵CH=BH,∴S△ACH=S△ACB=1.∵OC=CH,∴S△AOC=S△ACH=,∴S△AOH=S△AOC+S△ACH=,∴ =,解得k=3.
x
O
y
G
D
E
C
A
B
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
