浙教版九上数学每日一题76-80 二次函数与几何图形的综合(含解析)
文档属性
| 名称 | 浙教版九上数学每日一题76-80 二次函数与几何图形的综合(含解析) | 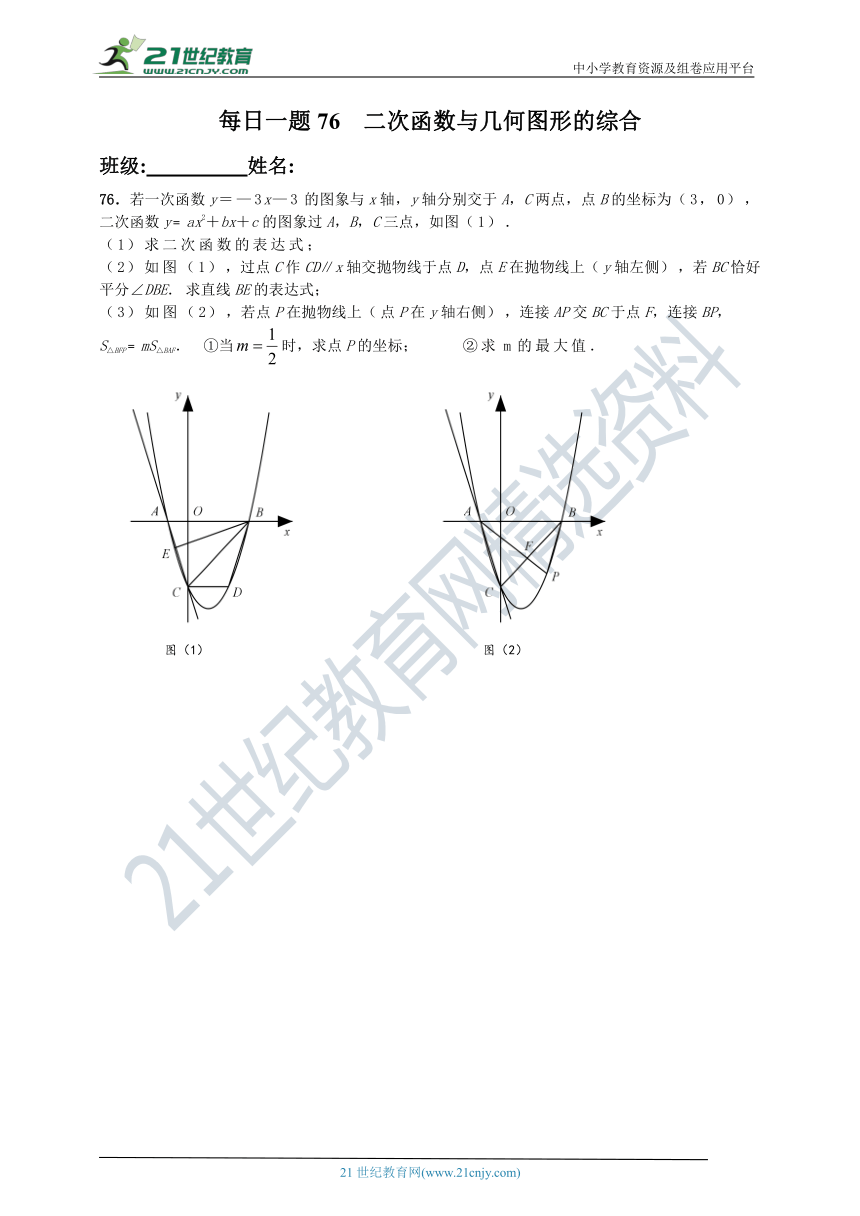 | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 11:21:11 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
每日一题76 二次函数与几何图形的综合
班级: 姓名:
76.若一次函数y=—3x—3的图象与x轴,y轴分别交于A,C两点,点B的坐标为(3,0),二次函数y﹦ax2+bx+c的图象过A,B,C三点,如图(1).
(1)求二次函数的表达式;
(2)如图(1),过点C作CD∥x轴交抛物线于点D,点E在抛物线上(y轴左侧),若BC恰好平分∠DBE.求直线BE的表达式;
(3)如图(2),若点P在抛物线上(点P在y轴右侧),连接AP交BC于点F,连接BP,
S△BFP﹦mS△BAF. ①当时,求点P的坐标; ②求m的最大值.
图(1) 图(2)
每日一题77 二次函数与几何图形的综合
班级: 姓名:
77.已知抛物线y=ax2+bx+c与x轴交于A(-1,0),B(5,0)两点,C为抛物线的顶点,抛物线的对称轴交x轴于点D,连结BC,且tan∠CBD=,如图所示.
(1)求抛物线的解析式;
(2)设P是抛物线的对称轴上的一个动点.
①过点P作x轴的平行线交线段BC于点E,过点E作EF⊥PE交抛物线于点F,连接FB、FC,求△BCF的面积的最大值;
②连接PB,求PC+PB的最小值.
每日一题78 二次函数与几何图形的综合
班级: 姓名:
78.在平面直角坐标系中,O为坐标原点,直线OA交二次函数y=x 的图像于点A,∠AOB=90°,点B在该二次函数的图像上,设过点(0,m)(其中m>0)且平行于x轴的直线交直线OA于点M,交直线OB于点N,以线段OM、ON为邻边作矩形OMPN.
(1)若点A的横坐标为8.
①用含m的代数式表示M的坐标;
②点P能否落在该二次函数的图像上?若能,求出m的值;若不能,请说明理由;
(2)当m=2时,若点P恰好落在该二次函数的图像上,请直接写出此时满足条件的所有直线OA的函数表达式.
每日一题79 二次函数与几何图形的综合
班级: 姓名:
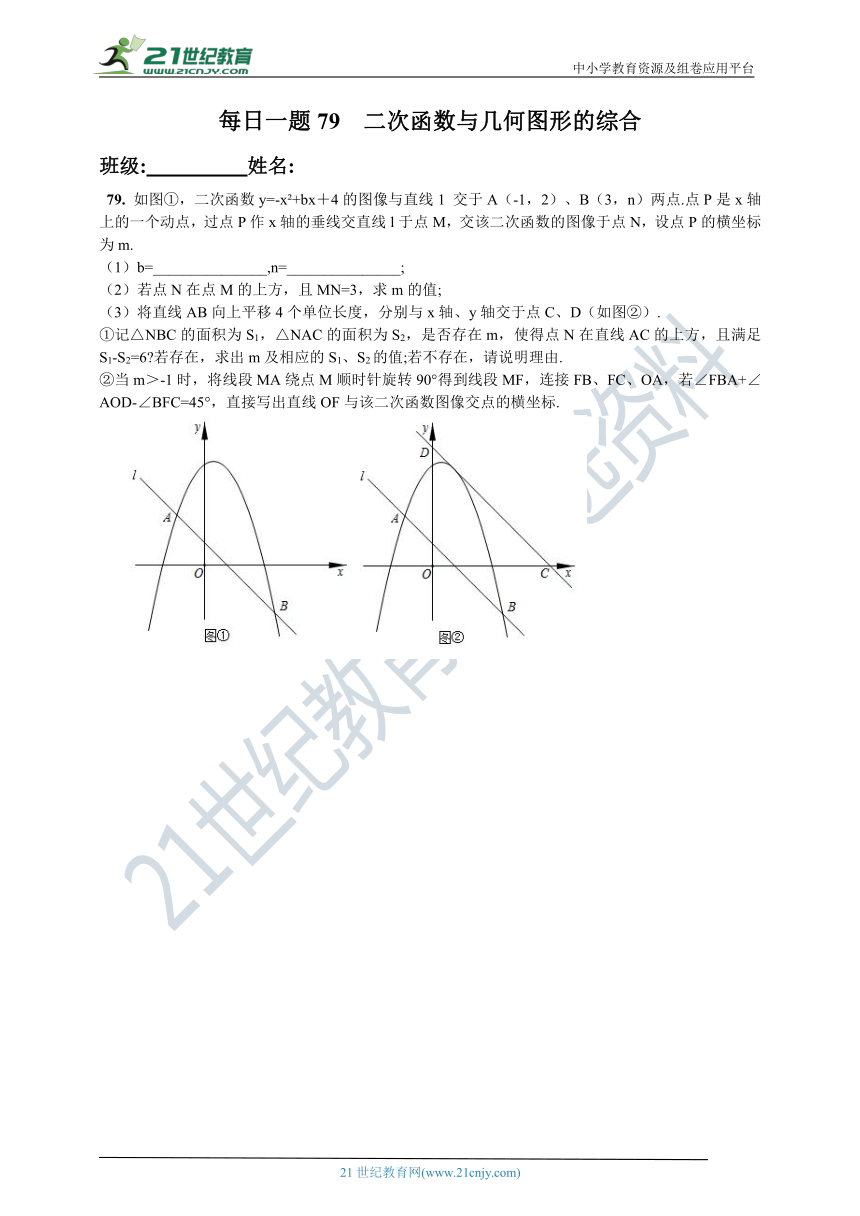
79. 如图①,二次函数y=-x +bx+4的图像与直线1 交于A(-1,2)、B(3,n)两点.点P是x轴上的一个动点,过点P作x轴的垂线交直线l于点M,交该二次函数的图像于点N,设点P的横坐标为m.
(1)b=_______________,n=_______________;
(2)若点N在点M的上方,且MN=3,求m的值;
(3)将直线AB向上平移4个单位长度,分别与x轴、y轴交于点C、D(如图②).
①记△NBC的面积为S1,△NAC的面积为S2,是否存在m,使得点N在直线AC的上方,且满足S1-S2=6 若存在,求出m及相应的S1、S2的值;若不存在,请说明理由.
②当m>-1时,将线段MA绕点M顺时针旋转90°得到线段MF,连接FB、FC、OA,若∠FBA+∠AOD-∠BFC=45°,直接写出直线OF与该二次函数图像交点的横坐标.
每日一题80 二次函数与几何图形的综合
班级: 姓名:
80.如图,直线y=-x+2交y轴于点A,交x轴于点C,抛物线y=-x2+bx+c经过点A,点C,且交x轴于另一点B.
(1)直接写出点点A,点B,点C的坐标及抛物线的解析式;
(2)在直线AC上方的抛物线上有一点M,求四边形ABCM面积的最大值及此时点M的坐标;
(3)将线段OA绕x轴上的动点P(m,0)顺时针旋转90°得到线段,若线段与抛物线只有一个公共点,请结合图象,求m的取值范围.
每日一题76 答案
76.(1)解:令—3x—3=0,得x=—1.令x=0时,y=—3.
∴A(—1,0),C(0,—3).
∵抛物线过点C(0,—3), ∴c=—3.
则y﹦ax2+bx—3,将A(—1,0),B(3,0)代入
得 解得
∴二次函数的表达式为y﹦x2—2x—3.
(2)解:设BE交OC于点M.
∵B(3,0),C(0,—3),∴OB=OC,∠OBC﹦∠OCB﹦45°.
∵CD∥AB, ∴∠BCD﹦45°. ∴∠OCB﹦∠BCD.
∵BC平分∠DBE,∴∠EBC﹦∠DBC.
又∵BC﹦BC, ∴△MBC≌△DBC.∴CM﹦CD.
由条件得:D(2,—3). ∴CD﹦CM﹦2. ∴OM﹦3—2﹦1.
∴M(0,—1). ∵B(3,0),∴直线BE解析式为y﹦x—1.
(3)①∵S△BFP﹦S△BAF, ∴PF﹦AF.
过点P作PN∥AB交BC于点N,则△ABF∽△PNF.∴AB﹦2NP.
∵AB﹦4,∴NP﹦2.
∵直线BC的表达式为y=x—3, 设P(t,t2—2t—3),
∴t2—2t—3=xN—3.∴xN=t2—2t.
∴PN﹦t—(t2—2t),则t—(t2—2t)﹦2,解得t1﹦2,t2﹦1.
∴点P(2,—3)或P(1,—4).
②由①得:m=.
∴m====×﹝—(t—)2+﹞=—(t—)2+. ∴m有最大值,m最大值=.
每日一题77 答案
77.解:(1)根据题意,可设抛物线的解析式为:y=a(x+1)(x-5),
∵CD是抛物线的对称轴,∴D(2,0);
又∵tan∠CBD=,∴CD=BDtan∠CBD=4,即C(2,4),
代入抛物线的解析式,得4=a(2+1)(2-5),解得a=-,
∴二次函数的解析式为y=-(x+1)(x-5),即y=-x2+x+;
(2)①设直线BC的解析式为y=kx+b,
∴ 解得 EQ \B\lc\{(\a\al(k=-,,b=. )) 即直线BC的解析式为y=-x+,
设E坐标为(t,-t+),则F点坐标为(t,-t2+t+),
∴EF=(-t2+t+)-(-t+)=-t2+t-,
∴S△BCF=×EF×BD=×3×(-t2+t-)=-(t-)2+,
∴当t=时,△BCF的面积最大,且最大值为;
②如图,连接AC,根据图形的对称性可知 ∠ACD=∠BCD,AC=BC=5,
∴sin∠ACD= =,
过点P作PG⊥AC于G,过点B作BH⊥AC于点H,
则在Rt△PCG中,PG=PCsin∠ACD=PC,
∴PC+PB=PG+PB≥BH,
由此可知当B、P、H三点共线时PC+PB的值最小,即线段BH的长.
∵S△ABC=×AB×CD=×6×4=12,又S△ABC=×AC×BH=BH,
∴BH=12,即BH=,∴PC+PB的最小值为.
每日一题78 答案
78.解:(1)①M( m,m);
②N(—2m,m),∴P(- m,2m)【平行四边形顶点公式】,代入抛物线解得m=;
(2)①当点A在y轴右侧时,设A(a, a2),所以直线OA解析式为y=ax,∴M(,2),再求出B(-,),∴直线OB的解析式为y=-x,同理求得N(-,2);∴P(-,4),代入抛物线得-=4,解得a=4±4,∴直线OA解析式为y=(±1)x;
、
②当点A在y轴左侧时,即为①中点B位置,∴直线OA的解析式为y=-x =-(±1)x;
综上所述,直线OA的解析式为y=(±1)x或(±1)x.
每日一题79 答案
79.(1)b=1,n=-2;
(2)直线AB:y=-x+1,N(m,-m2+m+4),M(m,-m+1),
MN=-m2+m+4-(-m+1)=-m2+2m+3=3,解得m1=0,m2=2.
(3)①S1-S2=S△GBC-S△GAN=S△ABC-S△ABN=6,因为S△ABC=8,所以S△ABN=2,
S△ABN=·MN·(xB-xA)=(-m2+2m+3)×4=2,可解出m的值.
②AF∥x轴,∠FBA=a,∠AOD=b,∠BFC=c,tanB=,a+b-c=45°.
a-45°=c-b ∠MBG=45°,BG∥FH,FH⊥x轴,
因为a-45°=∠GBF=∠HFB=c-∠CFH=c-b,所以∠CFH=b,即tan∠CFH=,
因为FH=2,所以CH=1,得F(4,2).
每日一题80 答案
80.解:(1)在y=-x+2中,令x=0,得y=2;令y=0,得x=4,从而A(0,2),C(4,0).由抛物线y=-x2+bx+c经过点A,点C,得,解得,从而抛物线的解析式为y=-x2+x+2,令y=0,得x=4或-2,于是B(-2,0).
综上,A(0,2),B(-2,0),C(4,0),抛物线的解析式为y=-x2+x+2.
(2)如答图1,过M作MN⊥BC于点N.令M(m,-m2+m+2),则S△AOB=2,S梯形AMNO=(2+y)m,S△CMN=(4-m)y,∴S四边形ABCM=2+(2+y)m+(4-m)y=2+m+my+2y-my=2y+m+2=2(-m2+m+2)+m+2=-m2+2m+6=-(m-2)2+8.∵-<0,∴当m=2时,S四边形ABCM|max=8,此时M(2,2).
(3)如答图2,当点在抛物线上时,易证明△OPA≌△,从而(m+2,m),于是m=-(m+2)2+(m+2)+2,整理,得m2+6m-8=0,解得m=-3±;如答图3,当点在抛物线上时,有(m,m),于是m=-m2+m+2,整理,得m2+2m-8=0,解得m=-4或2.综上,线段与抛物线只有一个公共点时,m的取值范围是-3+≤m≤2或-3-≤m≤-4.
第80题图 第80题备用图
图(2)
图(1)
第80题答图1
第80题答图2 第80题答图3
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
每日一题76 二次函数与几何图形的综合
班级: 姓名:
76.若一次函数y=—3x—3的图象与x轴,y轴分别交于A,C两点,点B的坐标为(3,0),二次函数y﹦ax2+bx+c的图象过A,B,C三点,如图(1).
(1)求二次函数的表达式;
(2)如图(1),过点C作CD∥x轴交抛物线于点D,点E在抛物线上(y轴左侧),若BC恰好平分∠DBE.求直线BE的表达式;
(3)如图(2),若点P在抛物线上(点P在y轴右侧),连接AP交BC于点F,连接BP,
S△BFP﹦mS△BAF. ①当时,求点P的坐标; ②求m的最大值.
图(1) 图(2)
每日一题77 二次函数与几何图形的综合
班级: 姓名:
77.已知抛物线y=ax2+bx+c与x轴交于A(-1,0),B(5,0)两点,C为抛物线的顶点,抛物线的对称轴交x轴于点D,连结BC,且tan∠CBD=,如图所示.
(1)求抛物线的解析式;
(2)设P是抛物线的对称轴上的一个动点.
①过点P作x轴的平行线交线段BC于点E,过点E作EF⊥PE交抛物线于点F,连接FB、FC,求△BCF的面积的最大值;
②连接PB,求PC+PB的最小值.
每日一题78 二次函数与几何图形的综合
班级: 姓名:
78.在平面直角坐标系中,O为坐标原点,直线OA交二次函数y=x 的图像于点A,∠AOB=90°,点B在该二次函数的图像上,设过点(0,m)(其中m>0)且平行于x轴的直线交直线OA于点M,交直线OB于点N,以线段OM、ON为邻边作矩形OMPN.
(1)若点A的横坐标为8.
①用含m的代数式表示M的坐标;
②点P能否落在该二次函数的图像上?若能,求出m的值;若不能,请说明理由;
(2)当m=2时,若点P恰好落在该二次函数的图像上,请直接写出此时满足条件的所有直线OA的函数表达式.
每日一题79 二次函数与几何图形的综合
班级: 姓名:
79. 如图①,二次函数y=-x +bx+4的图像与直线1 交于A(-1,2)、B(3,n)两点.点P是x轴上的一个动点,过点P作x轴的垂线交直线l于点M,交该二次函数的图像于点N,设点P的横坐标为m.
(1)b=_______________,n=_______________;
(2)若点N在点M的上方,且MN=3,求m的值;
(3)将直线AB向上平移4个单位长度,分别与x轴、y轴交于点C、D(如图②).
①记△NBC的面积为S1,△NAC的面积为S2,是否存在m,使得点N在直线AC的上方,且满足S1-S2=6 若存在,求出m及相应的S1、S2的值;若不存在,请说明理由.
②当m>-1时,将线段MA绕点M顺时针旋转90°得到线段MF,连接FB、FC、OA,若∠FBA+∠AOD-∠BFC=45°,直接写出直线OF与该二次函数图像交点的横坐标.
每日一题80 二次函数与几何图形的综合
班级: 姓名:
80.如图,直线y=-x+2交y轴于点A,交x轴于点C,抛物线y=-x2+bx+c经过点A,点C,且交x轴于另一点B.
(1)直接写出点点A,点B,点C的坐标及抛物线的解析式;
(2)在直线AC上方的抛物线上有一点M,求四边形ABCM面积的最大值及此时点M的坐标;
(3)将线段OA绕x轴上的动点P(m,0)顺时针旋转90°得到线段,若线段与抛物线只有一个公共点,请结合图象,求m的取值范围.
每日一题76 答案
76.(1)解:令—3x—3=0,得x=—1.令x=0时,y=—3.
∴A(—1,0),C(0,—3).
∵抛物线过点C(0,—3), ∴c=—3.
则y﹦ax2+bx—3,将A(—1,0),B(3,0)代入
得 解得
∴二次函数的表达式为y﹦x2—2x—3.
(2)解:设BE交OC于点M.
∵B(3,0),C(0,—3),∴OB=OC,∠OBC﹦∠OCB﹦45°.
∵CD∥AB, ∴∠BCD﹦45°. ∴∠OCB﹦∠BCD.
∵BC平分∠DBE,∴∠EBC﹦∠DBC.
又∵BC﹦BC, ∴△MBC≌△DBC.∴CM﹦CD.
由条件得:D(2,—3). ∴CD﹦CM﹦2. ∴OM﹦3—2﹦1.
∴M(0,—1). ∵B(3,0),∴直线BE解析式为y﹦x—1.
(3)①∵S△BFP﹦S△BAF, ∴PF﹦AF.
过点P作PN∥AB交BC于点N,则△ABF∽△PNF.∴AB﹦2NP.
∵AB﹦4,∴NP﹦2.
∵直线BC的表达式为y=x—3, 设P(t,t2—2t—3),
∴t2—2t—3=xN—3.∴xN=t2—2t.
∴PN﹦t—(t2—2t),则t—(t2—2t)﹦2,解得t1﹦2,t2﹦1.
∴点P(2,—3)或P(1,—4).
②由①得:m=.
∴m====×﹝—(t—)2+﹞=—(t—)2+. ∴m有最大值,m最大值=.
每日一题77 答案
77.解:(1)根据题意,可设抛物线的解析式为:y=a(x+1)(x-5),
∵CD是抛物线的对称轴,∴D(2,0);
又∵tan∠CBD=,∴CD=BDtan∠CBD=4,即C(2,4),
代入抛物线的解析式,得4=a(2+1)(2-5),解得a=-,
∴二次函数的解析式为y=-(x+1)(x-5),即y=-x2+x+;
(2)①设直线BC的解析式为y=kx+b,
∴ 解得 EQ \B\lc\{(\a\al(k=-,,b=. )) 即直线BC的解析式为y=-x+,
设E坐标为(t,-t+),则F点坐标为(t,-t2+t+),
∴EF=(-t2+t+)-(-t+)=-t2+t-,
∴S△BCF=×EF×BD=×3×(-t2+t-)=-(t-)2+,
∴当t=时,△BCF的面积最大,且最大值为;
②如图,连接AC,根据图形的对称性可知 ∠ACD=∠BCD,AC=BC=5,
∴sin∠ACD= =,
过点P作PG⊥AC于G,过点B作BH⊥AC于点H,
则在Rt△PCG中,PG=PCsin∠ACD=PC,
∴PC+PB=PG+PB≥BH,
由此可知当B、P、H三点共线时PC+PB的值最小,即线段BH的长.
∵S△ABC=×AB×CD=×6×4=12,又S△ABC=×AC×BH=BH,
∴BH=12,即BH=,∴PC+PB的最小值为.
每日一题78 答案
78.解:(1)①M( m,m);
②N(—2m,m),∴P(- m,2m)【平行四边形顶点公式】,代入抛物线解得m=;
(2)①当点A在y轴右侧时,设A(a, a2),所以直线OA解析式为y=ax,∴M(,2),再求出B(-,),∴直线OB的解析式为y=-x,同理求得N(-,2);∴P(-,4),代入抛物线得-=4,解得a=4±4,∴直线OA解析式为y=(±1)x;
、
②当点A在y轴左侧时,即为①中点B位置,∴直线OA的解析式为y=-x =-(±1)x;
综上所述,直线OA的解析式为y=(±1)x或(±1)x.
每日一题79 答案
79.(1)b=1,n=-2;
(2)直线AB:y=-x+1,N(m,-m2+m+4),M(m,-m+1),
MN=-m2+m+4-(-m+1)=-m2+2m+3=3,解得m1=0,m2=2.
(3)①S1-S2=S△GBC-S△GAN=S△ABC-S△ABN=6,因为S△ABC=8,所以S△ABN=2,
S△ABN=·MN·(xB-xA)=(-m2+2m+3)×4=2,可解出m的值.
②AF∥x轴,∠FBA=a,∠AOD=b,∠BFC=c,tanB=,a+b-c=45°.
a-45°=c-b ∠MBG=45°,BG∥FH,FH⊥x轴,
因为a-45°=∠GBF=∠HFB=c-∠CFH=c-b,所以∠CFH=b,即tan∠CFH=,
因为FH=2,所以CH=1,得F(4,2).
每日一题80 答案
80.解:(1)在y=-x+2中,令x=0,得y=2;令y=0,得x=4,从而A(0,2),C(4,0).由抛物线y=-x2+bx+c经过点A,点C,得,解得,从而抛物线的解析式为y=-x2+x+2,令y=0,得x=4或-2,于是B(-2,0).
综上,A(0,2),B(-2,0),C(4,0),抛物线的解析式为y=-x2+x+2.
(2)如答图1,过M作MN⊥BC于点N.令M(m,-m2+m+2),则S△AOB=2,S梯形AMNO=(2+y)m,S△CMN=(4-m)y,∴S四边形ABCM=2+(2+y)m+(4-m)y=2+m+my+2y-my=2y+m+2=2(-m2+m+2)+m+2=-m2+2m+6=-(m-2)2+8.∵-<0,∴当m=2时,S四边形ABCM|max=8,此时M(2,2).
(3)如答图2,当点在抛物线上时,易证明△OPA≌△,从而(m+2,m),于是m=-(m+2)2+(m+2)+2,整理,得m2+6m-8=0,解得m=-3±;如答图3,当点在抛物线上时,有(m,m),于是m=-m2+m+2,整理,得m2+2m-8=0,解得m=-4或2.综上,线段与抛物线只有一个公共点时,m的取值范围是-3+≤m≤2或-3-≤m≤-4.
第80题图 第80题备用图
图(2)
图(1)
第80题答图1
第80题答图2 第80题答图3
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
